Zad.RGS.2012za sajt [Compatibility Mode]
|
|
|
- Полексија Божовић
- пре 5 година
- Прикази:
Транскрипт
1 n der lsov jednčin ( ) - b ( ) n nb n b b b n nb n 0 3 b b ) ( 1 b
2 Suirnje rezult priene n der lsove jednčine (1)N visoki tepertur i veliki zprein vdw prelzi u jednčinu idelnog gsnog stnj jer: N visoki tepertur privlčne sile odnosno čln / su znerljivi Ako je veliko, td je -b~ () ečnosti i gsovi postoje kd su privlčne i odbojne sile urvnotežene, konstnt odgovr privlčni b odbojni sil. (3) Kritične konstnte su povezne s vdw konstnt: z < izotere osiluju, prolzeći kroz iniu i ksiu koji konvergirju s približvnje i prvi i drugi izvod su jednki nuli Kritični kopresioni fktor Z / 3/8
3 Druge jednčine stnj So jednčine koje iju dve konstnte ogu biti izrežene u redukovno obliku.
4 rier 1. n der lsove konstnte i b su 1,390 L t ol - i 0,03913 L ol -1 z zot. Izrčunti korekioni čln z: A) zpreinu (u L) z 85,5 olov jedinjenj u blonu od 100 L n teperturi od 300 o C i B) pritisk (u t). A) Korekioni čln je: nb85,5ol 0,03913L/ol11,17 L B) n 1,39 L tol (85,5) ol u 11, 33t (100 L)
5 rier. Ako se neki gs ponš po n der lsovoj jednčini, zokruži tčno tvrñenje: 1)Gs se približv idelno ponšnju pri: ) visoko b) visoko ) niskoj d) ni jedno ) Jednčin z n olov gs glsi: ) n b) ( b) n n ( n b) n b n n ) d) e) ni jedn rier. Koji od sledećih gsov će pokzivti njveće negtivno odstupnje n dijgru / od? ) H O b) F ) CH 4 d) Ne e) Ar
6 rier 3. N teperturi od 300 K i pritisku od 0 t, kopresioni fktor je 0,86. Izrčunti zpreinu (u L) koju zuzi 8, ol gs pod ovi uslovi, Z Z Z 0,86 300K 1 1 0,86 8,314 JK ol 300 K 3 0,00106 / ol t n 8, 10 ol 0,00106 ol 8, 7L
7 rier 4. Jedn ol nekog gs n teperturi od 73K i pritisku od zuzi zpreinu od Ako je 0,50 6 ol -, izrčunti vrednost konstnte b. Iz.d.. jednčine sledi d je b: b p 4, , , , ol 1
8 rier 5. Koristeći n der lsove koefiijente z kiseonik (1,378 L t ol -, b 3, L ol -1 ) izrčunti: ) Bojlovu teperturu b) rdijus olekul gs pretpostvljjući d se olekuli ponšju ko krute sfere. ) 1 tl ol 1,378 57, K B br 3, Lol 8,06 10 LtK ol b) b 3, ol 9 3 vol 1, N 4 6,0 10 ol A r 3 1/ 3 1/ ol 1,3 10 1,47 10 v 4π 4π
9 rier 6. Kritične konstnte z ugljendioksid su: 7, , 94,0 3 /ol i 304, K. Izrčunti vn der lsove koefiijente i proeniti rdijus olekul gs (dti sve u SI). Rešenj: b /8 4, /ol 7R /64 0,37 6 ol - v ol b/4n A 4, ol -1 /4 6, ol -1 1, r 3 1/3 30 1/3 10 ol (,39 10 ) 1,33 10 v 4π
10 rier 7. Izrčunti pritisk 1,0 ol etn koji se ponš ko: ) u idelno gsno stnju; b) pre vn der lsovoj jednčini pod sledeći uslovi: i) n 73,15 K i,414 L i ii) n 1000 K i (5,489L ol - t, b6, L/ol) Doći!
11 rier 8. roeniti kritične konstnte gs iz n der lsovih pretr 0,751tL ol - i b0,06 Lol -1 (Sve dti u SI). 3b 3 0,06Lol 7b 10K 8 7Rb 1 0,751L tol 7 (0,06Lol 0,0678Lol 1 ) 1 6, ,5 t 5 3 5, ,75L tol ,08LtK ol 0,06Lol 1 / ol, 6
12 rier 9. Izrčunti pritisk n koe se nlzi 1 ol SO, ko zuzi zpreinu od 10 d 3 n 100 o C, upotrebljvjući jednčinu idelnog gsnog stnj, vn der lsovu jednčinu i Diteričijevu jednčinu. Z SO konstnte su: 6, kol -, b0, kol -1. re jednčini idelnod gsnog stnj pritisk je: 3,10 10 re n der lsovoj jednčini pritisk je: re Diteričijevoj jednčini pritisk je: 5 8, ,15 0,678 3, b 0,01 5, , e b 310,3691 0, e 0,678 31, ,7084 0, ,
13 rier 10. Odrediti zpreinu koju zuzi 1 ol kiseonik n -88 o C i n pritisku od 45,3 10 5, ko je kritičn tepertur 154,4 K kritični pritisk 5, re n der lsovoj jednčini zprein se rčun n osnovu fktor stišljivosti. Fktor stišljivosti se očitv s krive iz vrednosti z redukovni pritisk i teperturu: R 4 3 1, R 0,9 Z 0,8 Z,7 10 ol 1 Z 1,0 3,0 r 1,5 1,3 1, 1,1 1,0 r, r
14 rier 11: Gsovi A, B, C i D se ponšju pre n der lsovoj jednčini s konstnt i b dti u tblii: Gs A B C D (br 6 ol - ) ,05 b ( 3 ol -1 ) 0,050 0,15 0,10 0,0 ) Koji gs i njvišu kritičnu teperturu? b) Koji gs i njveće olekule? ) Koji gs je njpribližniji idelno gsno stnju n S? ) ošto je /b, gs A i njveće i njnje b, to on i njvišu. b) eličin olekul je odreñen konstnto b, p gs B i njveće olekule. ) Gs koji i njniže kritičnu teperturu i pritisk njbliži je IGS. Kko je / b i /b to je gs D njbliži IGS
15 rier 1. Z gs, koji se pokorv n der lsovoj jednčini i i 30 br, 473 K, kopresioni fktor / je veći od jedn z uslove: A) ) 50 br 53 K b) 1 br 373 K ) 500 br 773 K Gs će se približvti idelnosti pri: B) ) niskoj b) niskoj gustini ) nisko kopresiono fktoru d) ni jedno C)Izrčunti konstntu b (L/ol) z ovj gs.
16 A) Z je veće od jedn pri njviše pritisku i njvišoj teperturi, tj. 500 br i 773 K koje su veće od kritičnih B) Gs se približv idelnosti pri niskoj gustini tj. pritisku C) Iz vrednosti kopresionog fktor u kritičnoj tčki ože d se nñe konstnt b: 3 8, b b 0, / ol 0,164 L / ol
17 rier 13. Z gsoviti CO vn der lsove konstnte su b 0,0486 l ol 1 i 3,658 br l ol. N kojoj teperture će drugi virijlni koefiijent biti jednk nuli B()0 z B - 3,658 br l ol 106, K B Rb 8,314 0,0486 l ol 6-1
18 rier 14. Gs NO i 64 br, 177 K gs CCl 4 i 45 br i 550 K. A) Koji gs i nju konstntu b? B) I nju vrednost konstnte? C) I veću kritičnu zpreinu? D) Se skoro idelno ponš n 300K i 10 br-?
19 A) Kko je: 3b 7b 8 7Rb to je b srzerno odnosu /. Kko je: NO 177,76 64 CCl , b NO b CCl 4
20 B) Kko je konstnt srzern odnosu / to je: NO ,5 CCl , NO CCl4 C) (CCl 4 ) 38, (NO) 8, (CCl 4 )> (NO) D) Gs NO je bliži idelno ponšnju n 300K jer je t tepertur već od njegove kritične teperture.
21 rier 15. Izrziti α (kubni koefiijent širenj) i κ (koefiijent izoterske kopresibilnosti) (i) z ideln gs (ii) z gs z koji vži jednčin stnj: p ( b). R R 1 1 α α (i) p p 1 1 κ κ (ii) b R b R R b R b b b 1 κ α
(Microsoft Word - Vietove formule. Rastavljanje kvadratnog trinoma na lenear\205)
 VIETOVE FORMULE. RASTAVLJANJE KVARATNOG TRINOMA NA LINEARNE ČINIOCE Brojev su rešenj kvdrtne jednčine + + ko i so ko je + i Ove dve jednkosti zovu se Vietove forule. Čeu one služe? Osnovn prien je d n
VIETOVE FORMULE. RASTAVLJANJE KVARATNOG TRINOMA NA LINEARNE ČINIOCE Brojev su rešenj kvdrtne jednčine + + ko i so ko je + i Ove dve jednkosti zovu se Vietove forule. Čeu one služe? Osnovn prien je d n
Microsoft Word - MATRICE ZADACI ii deo
 MATRICE ZADACI ( II DEO) REŠAVANJE SISTEMA LINEARNIH ALGEBARSKIH JEDNAČINA Siste od jednčin s n nepozntih je njčešće uopšteno dt s: x + x +... + x = b n n x + x +... + x = b... n n x + x +... + x = b n
MATRICE ZADACI ( II DEO) REŠAVANJE SISTEMA LINEARNIH ALGEBARSKIH JEDNAČINA Siste od jednčin s n nepozntih je njčešće uopšteno dt s: x + x +... + x = b n n x + x +... + x = b... n n x + x +... + x = b n
Microsoft Word - VALJAK.doc
 ALJAK ljk je geometrijsko telo ogrničeno s dv krug u prlelnim rvnim i delom cilindrične površi čije su izvodnice normlne n rvn tih krugov. Os vljk je prv koj prolzi kroz centre z. Nrvno ko i do sd oznke
ALJAK ljk je geometrijsko telo ogrničeno s dv krug u prlelnim rvnim i delom cilindrične površi čije su izvodnice normlne n rvn tih krugov. Os vljk je prv koj prolzi kroz centre z. Nrvno ko i do sd oznke
(Microsoft Word - RE\212AVANJE SISTEMA JEDNACINA _metoda det._)
 EŠAVANJE SISTEMA JENAČINA ( METOA ETEMINANTI) U prethodni fjlovi so govorili kko se rešvju sistei upotrebo tric. U ovo fjlu ćeo pokušti d v objsnio kko se prienjuju deterinnte n rešvnje siste linernih
EŠAVANJE SISTEMA JENAČINA ( METOA ETEMINANTI) U prethodni fjlovi so govorili kko se rešvju sistei upotrebo tric. U ovo fjlu ćeo pokušti d v objsnio kko se prienjuju deterinnte n rešvnje siste linernih
1. Realni brojevi
 .. Skupovi brojev N {, 2,,...,n, n +,...} Skup prirodnih brojev ztvoren je s obzirom n opercije zbrjnj i množenj. To znči d se bilo koj dv broj ili više njih) mogu zbrjti i množiti i ko rezultt opet dobivmo
.. Skupovi brojev N {, 2,,...,n, n +,...} Skup prirodnih brojev ztvoren je s obzirom n opercije zbrjnj i množenj. To znči d se bilo koj dv broj ili više njih) mogu zbrjti i množiti i ko rezultt opet dobivmo
(Microsoft Word - VI\212ESTRUKI INTEGRALI- zadaci _ I deo_.doc)
 VIŠESTRUKI INTEGRALI - ZAACI ( I EO) vostruki integrli-odredjivnje grnic integrcije Prv stvr s kojom se susrećemo kod dvojnih integrl je odredjivnje grnice integrcije. Z skoro svki zdtk mormo crtti sliku
VIŠESTRUKI INTEGRALI - ZAACI ( I EO) vostruki integrli-odredjivnje grnic integrcije Prv stvr s kojom se susrećemo kod dvojnih integrl je odredjivnje grnice integrcije. Z skoro svki zdtk mormo crtti sliku
IV 3. Prostor matrica datog tipa nad poljem. Neka je dato polje (F, +, ) i neka su m, n N. Pravougaona šema mn skalara iz polja F, koja se sastoji od
 IV 3 Prostor mtric dtog tip nd poljem Nek je dto polje (F, +, ) i nek su m, n N Prvougon šem mn sklr iz polj F, koj se sstoji od m vrst i n kolon zpisn ko A = 211 22 2n ili A = 21 22 2n m1 m2 mn m1 m2
IV 3 Prostor mtric dtog tip nd poljem Nek je dto polje (F, +, ) i nek su m, n N Prvougon šem mn sklr iz polj F, koj se sstoji od m vrst i n kolon zpisn ko A = 211 22 2n ili A = 21 22 2n m1 m2 mn m1 m2
Microsoft Word - INTEGRALI ZADACI - v deo
 INTEGRALI ZADACI (V-DEO) Inegrli nekih funkij koje sdrže kvdrni rinom Njpre ćemo proučii inegrle oblik: I= i I = Kod njih se kvdrni rinom svede n knonični oblik pomoću formule: b 4 b = + + 4 nrvno, možemo
INTEGRALI ZADACI (V-DEO) Inegrli nekih funkij koje sdrže kvdrni rinom Njpre ćemo proučii inegrle oblik: I= i I = Kod njih se kvdrni rinom svede n knonični oblik pomoću formule: b 4 b = + + 4 nrvno, možemo
Microsoft Word - INTEGRALI ZADACI - v deo
 INTEGRALI ZADACI (V-DEO) Inegrli nekih funkcij koje sdrže kvdrni rinom b c Njpre ćemo proučii inegrle oblik: I i I b c b c Kod njih se kvdrni rinom b c svede n knonični oblik pomoću formule: b c b b c
INTEGRALI ZADACI (V-DEO) Inegrli nekih funkcij koje sdrže kvdrni rinom b c Njpre ćemo proučii inegrle oblik: I i I b c b c Kod njih se kvdrni rinom b c svede n knonični oblik pomoću formule: b c b b c
Microsoft Word - integrali IV deo.doc
 INTEGRALI ZADAI ( IV DEO) Integrcij rcionlne funkcije P( ) Rcionln funkcij je oblik Q( ). Može biti prv i neprv. Prv rcionln funkcij je on kod koje je mksimlni stepen polinom P() mnji od mksimlnog stepen
INTEGRALI ZADAI ( IV DEO) Integrcij rcionlne funkcije P( ) Rcionln funkcij je oblik Q( ). Može biti prv i neprv. Prv rcionln funkcij je on kod koje je mksimlni stepen polinom P() mnji od mksimlnog stepen
Microsoft Word - 16ms321
 Zdtk 3 (4, 4, TUPŠ) Duljine strni trokut jesu.5 m, 0 m i 8.5 m. Rzlik duljin njdulje i njkrće strnie njemu sličnog trokut iznosi 4.8 m. Kolik je duljin treće strnie (strnie srednje duljine) sličnog trokut?.
Zdtk 3 (4, 4, TUPŠ) Duljine strni trokut jesu.5 m, 0 m i 8.5 m. Rzlik duljin njdulje i njkrće strnie njemu sličnog trokut iznosi 4.8 m. Kolik je duljin treće strnie (strnie srednje duljine) sličnog trokut?.
Microsoft Word - GEOMETRIJA 3.4..doc
 4. UČENIK UME DA IZRAČUNA POVRŠINU I ZAPREMINU PRIZME I PIRAMIDE U SLUČAJEVIMA KADA NEOPODNI ELEMENTI NISU DATI KOCKA D= d = P= 6 V= mrež kocke Kock im 1 ivic dužine. Ml dijgonl ( dijgonl onove) je d =.
4. UČENIK UME DA IZRAČUNA POVRŠINU I ZAPREMINU PRIZME I PIRAMIDE U SLUČAJEVIMA KADA NEOPODNI ELEMENTI NISU DATI KOCKA D= d = P= 6 V= mrež kocke Kock im 1 ivic dužine. Ml dijgonl ( dijgonl onove) je d =.
Ime i prezime: Matični broj: Grupa: Datum:
 Lom i refleksij svjetlosti Cilj vježbe Primjen zkon geometrijske optike (lom i refleksij svjetlosti). Određivnje žrišne dljine tnke leće direktnom metodom. 1. Teorijski dio Zrcl i leće su objekti poznti
Lom i refleksij svjetlosti Cilj vježbe Primjen zkon geometrijske optike (lom i refleksij svjetlosti). Određivnje žrišne dljine tnke leće direktnom metodom. 1. Teorijski dio Zrcl i leće su objekti poznti
Slide 1
 DINAMIKA Dinmički sistem - pogon s motorom jednosmerne struje: N: u u f Dinmički sistem Ulzi Izlzi (?) i, ϕ[ i ], ωθ, m m f f U opštem slučju ovj dinmički sistem je NELINEARAN MATEMATIČKI MODEL POGONA
DINAMIKA Dinmički sistem - pogon s motorom jednosmerne struje: N: u u f Dinmički sistem Ulzi Izlzi (?) i, ϕ[ i ], ωθ, m m f f U opštem slučju ovj dinmički sistem je NELINEARAN MATEMATIČKI MODEL POGONA
Ortogonalni, Hermiteovi i Jacobijevi polinomi Safet Penjić Naučno-istraživački rad* koji je razvijen kao parcijalno ispunjenje obav
 Ortogonlni, Hermiteovi i Jcobijevi polinomi Sfet Penjić inforrt@gmil.com Nučno-istrživčki rd* koji je rzvijen ko prcijlno ispunjenje obvez prem izbornom predmetu Specijlne funkcije s postdiplomskog studij
Ortogonlni, Hermiteovi i Jcobijevi polinomi Sfet Penjić inforrt@gmil.com Nučno-istrživčki rd* koji je rzvijen ko prcijlno ispunjenje obvez prem izbornom predmetu Specijlne funkcije s postdiplomskog studij
Microsoft Word - Analiticka - formule.doc
 . Rtojnje izmeñu dve tčke d( A, B ( + (. Deljenje duži u dtoj zmei Ako je tčk M (, unutšnj tčk duži AB, gde je A(, i ko je dt zme AM AM : MB to jet (, u kojoj tčk M deli duž AB, ond e koodinte tčke M čunju
. Rtojnje izmeñu dve tčke d( A, B ( + (. Deljenje duži u dtoj zmei Ako je tčk M (, unutšnj tčk duži AB, gde je A(, i ko je dt zme AM AM : MB to jet (, u kojoj tčk M deli duž AB, ond e koodinte tčke M čunju
Zadatak 1 U jednodimenzionalnoj kutiji, širine a, nalazi se 1000 neutrona. U t = 0, stanje svake čestice je ψ(x, 0) = Ax(x a). a) Normirajte valnu fun
 Zdtk 1 U jednodimenzionlnoj kutiji, širine, nlzi se 1 neutron. U t, stnje svke čestice je ψ(x, ) Ax(x ). ) Normirjte vlnu funkciju ψ i ndite [ vrijednost konstnte A. b) Koliko čestic se nlzi u intervlu,
Zdtk 1 U jednodimenzionlnoj kutiji, širine, nlzi se 1 neutron. U t, stnje svke čestice je ψ(x, ) Ax(x ). ) Normirjte vlnu funkciju ψ i ndite [ vrijednost konstnte A. b) Koliko čestic se nlzi u intervlu,
Microsoft Word - BROJNI REDOVI zadaci _II deo_.doc
 BROJNI REDOVI ZADACI ( II DEO) Dlmbrov kritrijum Ako z rd ostoji lim + - z r > rd divrgir - z r odlučivo - z r < kovrgir r od vži: Primr. Isitti kovrgciju rd! Ršj: Njr d odrdimo. Ovd j to! ( zči uzimmo
BROJNI REDOVI ZADACI ( II DEO) Dlmbrov kritrijum Ako z rd ostoji lim + - z r > rd divrgir - z r odlučivo - z r < kovrgir r od vži: Primr. Isitti kovrgciju rd! Ršj: Njr d odrdimo. Ovd j to! ( zči uzimmo
Microsoft Word - 26ms281
 Zdtk 8 (Ivn, tehničk škol) Rcionlizirj rzlomk Rješenje 8 6 +, b b, b b Proširiti rzlomk znči brojnik i nzivnik tog rzlomk pomnožiti istim brojem rzličitim od nule i jedinice n b b n, n, n Zkon distribucije
Zdtk 8 (Ivn, tehničk škol) Rcionlizirj rzlomk Rješenje 8 6 +, b b, b b Proširiti rzlomk znči brojnik i nzivnik tog rzlomk pomnožiti istim brojem rzličitim od nule i jedinice n b b n, n, n Zkon distribucije
PLB146 Manual
 SRPSKI PLB-146M Uputstvo z montžu UPUTE ZA OTVARANJE PAKIRANJA! Pžljvo otvorite kutiju, izvdite njezin sdržj i rsporedite g n krton ili neku drugu zštitnu površinu (d biste izbj egli oštedenj).! Prem popisu
SRPSKI PLB-146M Uputstvo z montžu UPUTE ZA OTVARANJE PAKIRANJA! Pžljvo otvorite kutiju, izvdite njezin sdržj i rsporedite g n krton ili neku drugu zštitnu površinu (d biste izbj egli oštedenj).! Prem popisu
Microsoft Word - Kvalif_Zadaci_Rjesenja_TOI.docx
 Univerzitet u Tuzli ZBIRKA zdtk s prijemnih ispit iz Mtemtike n Fkultetu elektrotehnike u periodu od 0-0 godine (z studijski progrm "Tehnički odgoj i informtik") Tuzl, mj 08 TEHNIČKI ODGOJ I INFORMATIKA
Univerzitet u Tuzli ZBIRKA zdtk s prijemnih ispit iz Mtemtike n Fkultetu elektrotehnike u periodu od 0-0 godine (z studijski progrm "Tehnički odgoj i informtik") Tuzl, mj 08 TEHNIČKI ODGOJ I INFORMATIKA
Microsoft Word - PRIMENE SLICNOSTI NA PRAVOUGLI TROUGAO.doc
 PRIMENE SLIČNOSTI N PRVOUGLI TROUGO Nrjmo jedn prvougli rougo s sndrdnim oeležvnjim:, su kee je ipoenuz je ipoenuzin visin p i su odseči n ipoenuzi koje prvi visin β α α D p β Hipoenuzin visin D deli rougo
PRIMENE SLIČNOSTI N PRVOUGLI TROUGO Nrjmo jedn prvougli rougo s sndrdnim oeležvnjim:, su kee je ipoenuz je ipoenuzin visin p i su odseči n ipoenuzi koje prvi visin β α α D p β Hipoenuzin visin D deli rougo
Microsoft Word - Andrea Gelemanovic i Martina Hrkovac - Dvodimenzionalna valna jednadzba.doc
 Sveučilište u Zgreu Fkultet kemijskog inženjerstv i tehnologije Zvod z mtemtiku Mtemtičke metode u kemijskom inženjerstvu Dvodimenzionln vln jedndž Profesor: Dr.sc. Ivic Gusić Andre Geleović i Mrtin Hrkovc
Sveučilište u Zgreu Fkultet kemijskog inženjerstv i tehnologije Zvod z mtemtiku Mtemtičke metode u kemijskom inženjerstvu Dvodimenzionln vln jedndž Profesor: Dr.sc. Ivic Gusić Andre Geleović i Mrtin Hrkovc
Microsoft Word - KRIVOLINIJSKI INTEGRALI zadaci _I deo_.doc
 KRIVOLINIJSKI INTEGRALI ZADACI ( I DEO) Krivolinijski inegrli prve vrse. Izrčuni krivolinijski inegrl ds ko je deo prve = izmeñu čk (, ) i (,). D se podseimo: b Ako je kriv d u obliku : =() b d je: f (,
KRIVOLINIJSKI INTEGRALI ZADACI ( I DEO) Krivolinijski inegrli prve vrse. Izrčuni krivolinijski inegrl ds ko je deo prve = izmeñu čk (, ) i (,). D se podseimo: b Ako je kriv d u obliku : =() b d je: f (,
Zadatak 1 U jednodimenzionalnoj kutiji, širine a, nalazi se 1000 neutrona. U t = 0, stanje svake čestice je ψ(x, 0) = Ax(x a). a) Normirajte valnu fun
 Zdtk U jednodimenzionlnoj kutiji, širine, nlzi se 000 neutron. U t 0, stnje svke čestice je ψx, 0 Axx. Normirjte vlnu funkciju ψ i ndite [ vrijednost konstnte A. b Koliko čestic se nlzi u intervlu 0, ]
Zdtk U jednodimenzionlnoj kutiji, širine, nlzi se 000 neutron. U t 0, stnje svke čestice je ψx, 0 Axx. Normirjte vlnu funkciju ψ i ndite [ vrijednost konstnte A. b Koliko čestic se nlzi u intervlu 0, ]
Microsoft Word - Integrali III deo.doc
 INTEGRALI ZADACI (III-DEO) PARCIJALNA INTEGRACIJA Ako su u i diferencijbilne funkcije od, ond je : ud= u du O meod, prcijln inegrcij, po prilu je n počeku proučnj slbo rzumlji. Mi ćemo pokuši, koliko o
INTEGRALI ZADACI (III-DEO) PARCIJALNA INTEGRACIJA Ako su u i diferencijbilne funkcije od, ond je : ud= u du O meod, prcijln inegrcij, po prilu je n počeku proučnj slbo rzumlji. Mi ćemo pokuši, koliko o
Slide 1
 Kompleksi Prelazni metali Međusobno imaju slične osobine Dosta se razlikuju od alkalih i zemnoalkalnih metala Imaju visoku tačku topljenja,veliku gustinu, uglavnom veliku tvrdoću, dobri su provodnici
Kompleksi Prelazni metali Međusobno imaju slične osobine Dosta se razlikuju od alkalih i zemnoalkalnih metala Imaju visoku tačku topljenja,veliku gustinu, uglavnom veliku tvrdoću, dobri su provodnici
Microsoft Word - Obrazac_realizacije_4418
 ФОНД ЗДРАВСТВЕНОГ ОСИГУРАЊА РЕПУБЛИКЕ СРПСКЕ ТАБЕЛА РЕАЛИЗАЦИЈЕ УГОВОРА/ОКВИРНОГ СПОРАЗУМА Набавка лијекова са Основне болничке листе лијекова број: 07/015-4418/17 1 2 3 4 5 6 7 8 9 10 Остатак Опис Датум
ФОНД ЗДРАВСТВЕНОГ ОСИГУРАЊА РЕПУБЛИКЕ СРПСКЕ ТАБЕЛА РЕАЛИЗАЦИЈЕ УГОВОРА/ОКВИРНОГ СПОРАЗУМА Набавка лијекова са Основне болничке листе лијекова број: 07/015-4418/17 1 2 3 4 5 6 7 8 9 10 Остатак Опис Датум
Petar Stipanovid :: Rješenja 2. pismenog ispita iz MMF1 2010/ I2-1 Ako su Φ = r sin πφ + θ ; F = r 2 sin θ r + r cos φ θ + cos θ φ; M = log 2
 Petr Stipnovid :: Rješenj. pismenog ispit iz MMF / I - Ako su Φ = r sin φ + θ ; F = r sin θ r + r cos φ θ + cos θ φ; M = log sin x y+z ; E = ρ z ρ gdje su (r, θ, φ) Krtezijeve koordinte, (r, θ, φ) sferne
Petr Stipnovid :: Rješenj. pismenog ispit iz MMF / I - Ako su Φ = r sin φ + θ ; F = r sin θ r + r cos φ θ + cos θ φ; M = log sin x y+z ; E = ρ z ρ gdje su (r, θ, φ) Krtezijeve koordinte, (r, θ, φ) sferne
(Microsoft Word - EKSTREMUMI FUNKCIJA VI\212E PROMENLJIVIH _ii deo_.doc)
 EKSTREMUMI FUNKCIJA VIŠE PROMENLJIVIH ( II deo ) USLOVNI EKSTREMUM Ovde osim funkcije immo dte i uslove. Njčešće je to jedn uslov, li u oiljnijim primerim mogu iti dv i više njih. Ako je recimo dt funkcij
EKSTREMUMI FUNKCIJA VIŠE PROMENLJIVIH ( II deo ) USLOVNI EKSTREMUM Ovde osim funkcije immo dte i uslove. Njčešće je to jedn uslov, li u oiljnijim primerim mogu iti dv i više njih. Ako je recimo dt funkcij
(Microsoft Word - Dr\236avna matura - lipanj vi\232a razina - rje\232enja)
 . C. Intervl A tvore svi relni brojevi koji su jednki ili veći od i strogo mnji od 7. Intervl B tvore svi relni brojevi koji su strogo veći od i jednki ili veći od 5. Presjek tih intervl tvore relni brojevi
. C. Intervl A tvore svi relni brojevi koji su jednki ili veći od i strogo mnji od 7. Intervl B tvore svi relni brojevi koji su strogo veći od i jednki ili veći od 5. Presjek tih intervl tvore relni brojevi
PowerPoint Presentation
 Keijsko tehnološki fakultet Sveučilišta u Splitu Stručni studij keijske tehnologije i aterijala Stručni studij prehrabene tehnologije Fizika uditorne vježbe 4 Rad i energija. Sudari. Ivica Sorić (Ivica.Soric@fesb.hr)
Keijsko tehnološki fakultet Sveučilišta u Splitu Stručni studij keijske tehnologije i aterijala Stručni studij prehrabene tehnologije Fizika uditorne vježbe 4 Rad i energija. Sudari. Ivica Sorić (Ivica.Soric@fesb.hr)
DRŽAVNO NATJECANJE IZ MATEMATIKE Primošten, 4.travnja-6.travnja razred-rješenja OVDJE SU DANI NEKI NAČINI RJEŠAVANJA ZADATAKA. UKOLIKO UČENIK
 RŽVNO NTJENJE IZ MTEMTIKE Primošten, 4travnja-6travnja 016 7 razred-rješenja OVJE SU NI NEKI NČINI RJEŠVNJ ZTK UKOLIKO UČENIK IM RUGČIJI POSTUPK RJEŠVNJ, ČLN POVJERENSTV UŽN JE I TJ POSTUPK OOVTI I OIJENITI
RŽVNO NTJENJE IZ MTEMTIKE Primošten, 4travnja-6travnja 016 7 razred-rješenja OVJE SU NI NEKI NČINI RJEŠVNJ ZTK UKOLIKO UČENIK IM RUGČIJI POSTUPK RJEŠVNJ, ČLN POVJERENSTV UŽN JE I TJ POSTUPK OOVTI I OIJENITI
Microsoft Word - PRIMENA INTEGRALA.doc
 PRIMENA INTEGRALA P ngo što knmo s izčunvnjm povšin, dužin luk, zpmin ili povšin otcion povši momo odditi: - pomoću p tčk ispitmo tok i nctmo kivu kivko j to nophodno - gnic intgl nñmo ko šnj sistm jdnčin
PRIMENA INTEGRALA P ngo što knmo s izčunvnjm povšin, dužin luk, zpmin ili povšin otcion povši momo odditi: - pomoću p tčk ispitmo tok i nctmo kivu kivko j to nophodno - gnic intgl nñmo ko šnj sistm jdnčin
Stokesov teorem i primjene Stokesov teorem - iskaz pogledati u predavanjima (Teorem 21.7.) Zadatak 1 Izračunajte ukupni fluks funkcije F kroz plohu D,
 Stokesov teorem i primjene Stokesov teorem - iskz pogledti u predvnjim (Teorem 1.7.) Zdtk 1 Izrčunjte ukupni fluks funkcije F kroz plohu, ko je F zdno s F (x, y, z) ( y, x, x ), je unij cilindr x + y (pri
Stokesov teorem i primjene Stokesov teorem - iskz pogledti u predvnjim (Teorem 1.7.) Zdtk 1 Izrčunjte ukupni fluks funkcije F kroz plohu, ko je F zdno s F (x, y, z) ( y, x, x ), je unij cilindr x + y (pri
trougao.dvi
 Mtemtički fkultet Univerzitet u eogrdu Mster rd Trougo u nstvi mtemtike u osnovnoj i srednjoj školi Mentor: Student: Do. dr Srdjn Vukmirović Drgn Despotović 1048/2014 eogrd, 2015. Sdržj Uvod 2 1 Osnovn
Mtemtički fkultet Univerzitet u eogrdu Mster rd Trougo u nstvi mtemtike u osnovnoj i srednjoj školi Mentor: Student: Do. dr Srdjn Vukmirović Drgn Despotović 1048/2014 eogrd, 2015. Sdržj Uvod 2 1 Osnovn
untitled
 Osnovi konstruisnj Prolemi torelnije pri konstruisnju Složen odstupnj i merni lni Složen odstupnj su rezultti sirnj ili oduzimnj dveju ili više tolerisnih kot koje se u vidu ln nstvljju jedn n drugu u
Osnovi konstruisnj Prolemi torelnije pri konstruisnju Složen odstupnj i merni lni Složen odstupnj su rezultti sirnj ili oduzimnj dveju ili više tolerisnih kot koje se u vidu ln nstvljju jedn n drugu u
DJEČJI VRTIĆ TROGIR TROGIR Trogir, Klasa: UP/I /19-01/1 Urbroj Na temelju članka 1a, 20. i 35. stavka 1. podstavk
 DJEČJI VRTIĆ TROGIR TROGIR Trogir, 24. 04. 2019. Klasa: UP/I-034-01-01/19-01/1 Urbroj. 2184-17-19-1 Na temelju članka 1a, 20. i 35. stavka 1. podstavka 4. Zakona o predškolskom odgoju i obrazovanju (NN
DJEČJI VRTIĆ TROGIR TROGIR Trogir, 24. 04. 2019. Klasa: UP/I-034-01-01/19-01/1 Urbroj. 2184-17-19-1 Na temelju članka 1a, 20. i 35. stavka 1. podstavka 4. Zakona o predškolskom odgoju i obrazovanju (NN
Univerzitet u Nišu Prirodno - matematički Fakultet Departman za matematiku Višestruko osiguranje - Master rad - Mentor: dr Marija Milošević Niš, Mart
 Univerzitet u Nišu Prirodno - mtemtički Fkultet Deprtmn z mtemtiku Višestruko osigurnje - Mster rd - Mentor: dr Mrij Milošević Niš, Mrt 213. Student: An Jnjić 2 Sdržj 1 Uvod 5 2 Osnovni pojmovi 7 2.1 Motivcioni
Univerzitet u Nišu Prirodno - mtemtički Fkultet Deprtmn z mtemtiku Višestruko osigurnje - Mster rd - Mentor: dr Mrij Milošević Niš, Mrt 213. Student: An Jnjić 2 Sdržj 1 Uvod 5 2 Osnovni pojmovi 7 2.1 Motivcioni
1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan
 1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan jednačinom oblika: a 11 x 2 + 2a 12 xy + a 22 y 2
1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan jednačinom oblika: a 11 x 2 + 2a 12 xy + a 22 y 2
ISSN X Билтен Градске општине Барајево БРОЈ Септембар У БАРАЈЕВУ ПРОС АВ ЕНА С АВА И ДАН ОПШТИНЕ ИЗ РАДА СКУПШТИНЕ ГРАДСКЕ ОПШТИНЕ
 ISSN 1451-494X Билтен Градске општине Барајево БРОЈ 68-69 Септембар 2017. У БАРАЈЕВУ ПРОС АВ ЕНА С АВА И ДАН ОПШТИНЕ ИЗ РАДА СКУПШТИНЕ ГРАДСКЕ ОПШТИНЕ БАРАЈЕВО ГОДИНА ОД ОР ИРА А ПРВЕ СРПСКЕ В АДЕ У ВЕ
ISSN 1451-494X Билтен Градске општине Барајево БРОЈ 68-69 Септембар 2017. У БАРАЈЕВУ ПРОС АВ ЕНА С АВА И ДАН ОПШТИНЕ ИЗ РАДА СКУПШТИНЕ ГРАДСКЕ ОПШТИНЕ БАРАЈЕВО ГОДИНА ОД ОР ИРА А ПРВЕ СРПСКЕ В АДЕ У ВЕ
РЕПУБЛИКА СРБИЈА МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА СРПСКО ХЕМИЈСКО ДРУШТВО РЕПУБЛИЧКО ТАКМИЧЕЊЕ ИЗ ХЕМИЈЕ Лесковац, 31. мај и 1. јун
 РЕПУБЛИКА СРБИЈА МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА СРПСКО ХЕМИЈСКО ДРУШТВО РЕПУБЛИЧКО ТАКМИЧЕЊЕ ИЗ ХЕМИЈЕ Лесковац, 31. мај и 1. јун 2014. године ТЕСТ ЗНАЊА ЗА VIII РАЗРЕД Шифра ученика
РЕПУБЛИКА СРБИЈА МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА СРПСКО ХЕМИЈСКО ДРУШТВО РЕПУБЛИЧКО ТАКМИЧЕЊЕ ИЗ ХЕМИЈЕ Лесковац, 31. мај и 1. јун 2014. године ТЕСТ ЗНАЊА ЗА VIII РАЗРЕД Шифра ученика
OKFH2-12
 ELEKTRIČNE OSOBINE Električne osobine atoma i molekula uslovljavaju: ojavu dvojnog relamanja svetlosti ojavu olarizacije rasejane svetlosti dielektrične osobine međumolekulske interakcije ravila izbora
ELEKTRIČNE OSOBINE Električne osobine atoma i molekula uslovljavaju: ojavu dvojnog relamanja svetlosti ojavu olarizacije rasejane svetlosti dielektrične osobine međumolekulske interakcije ravila izbora
1
 PROVOđENJE TOPLOTE ovođenje toplote ili kondukcija je način kretanja toplote koji je svojstven čvrsti aterijalia, iako se pojavljuje (ali sa anearljivi inteniteto) i kod luida. Karakteristika aterijala
PROVOđENJE TOPLOTE ovođenje toplote ili kondukcija je način kretanja toplote koji je svojstven čvrsti aterijalia, iako se pojavljuje (ali sa anearljivi inteniteto) i kod luida. Karakteristika aterijala
Министарство просветe и спортa Републике Србије
 Министарство просветe и спортa Републике Србије Српско хемијско друштво Републичко такмичење из хемије 21.05.2005. Тест за I разред средње школе Име и презиме Место и школа Разред Не отварајте добијени
Министарство просветe и спортa Републике Србије Српско хемијско друштво Републичко такмичење из хемије 21.05.2005. Тест за I разред средње школе Име и презиме Место и школа Разред Не отварајте добијени
RITAM FORMS - PROIZVODNJA - NARUDŽBE I PLANIRANJE - PLAN PROIZVODNJE Stranica 1 od 10 Plan proizvodnje U pro esu proizvod je proizvodi astaju a os ovi
 RITAM FORMS - PROIZVODNJA - NARUDŽBE I PLANIRANJE - PLAN PROIZVODNJE Stranica 1 od 10 Plan proizvodnje U pro esu proizvod je proizvodi astaju a os ovi rad ih aloga koje ože o ruč o u ositi po potrebi.
RITAM FORMS - PROIZVODNJA - NARUDŽBE I PLANIRANJE - PLAN PROIZVODNJE Stranica 1 od 10 Plan proizvodnje U pro esu proizvod je proizvodi astaju a os ovi rad ih aloga koje ože o ruč o u ositi po potrebi.
Zadaci II
 Opšti kus fizičke heije Zadaci II ovšinski napon, viskoznost, adsopcija, fizičke osobine olekula Zadatak. ko se voda na 5 o C (gustine,997 gc ) podiže u kapilai adijusa, za 7,6 c, izačunati povšinski napon
Opšti kus fizičke heije Zadaci II ovšinski napon, viskoznost, adsopcija, fizičke osobine olekula Zadatak. ko se voda na 5 o C (gustine,997 gc ) podiže u kapilai adijusa, za 7,6 c, izačunati povšinski napon
Microsoft Word - 26ms441
 Zdtk 44 (Ktri, mturtic) Dijelimo li bombo osmero djece tko d svko dijete dobije jedki broj bombo, ostt će epodijelje bombo Kd bismo toj djeci dijelili 5 bombo tko d svko dijete dobije jedki broj bombo,
Zdtk 44 (Ktri, mturtic) Dijelimo li bombo osmero djece tko d svko dijete dobije jedki broj bombo, ostt će epodijelje bombo Kd bismo toj djeci dijelili 5 bombo tko d svko dijete dobije jedki broj bombo,
Zadaci
 Hemijski fakultet Univerziteta u Beogradu Prijemni ispit, 30. jun 2013. godine Test iz hemije Ime i prezime:. Redni broj prijave:. Napomena: Test raditi isključivo plavom ili crnom hemijskom olovkom. Vreme
Hemijski fakultet Univerziteta u Beogradu Prijemni ispit, 30. jun 2013. godine Test iz hemije Ime i prezime:. Redni broj prijave:. Napomena: Test raditi isključivo plavom ili crnom hemijskom olovkom. Vreme
PowerPoint Presentation
 REALNA FUNKCIJA Fukciju f čiji je skup vrijedosti V podskup skup R relih brojev zovemo relom fukcijom. Ako je, pritom, oblst defiisosti D eki podskup skup R uređeih -torki relih brojev, kžemo d je f rel
REALNA FUNKCIJA Fukciju f čiji je skup vrijedosti V podskup skup R relih brojev zovemo relom fukcijom. Ako je, pritom, oblst defiisosti D eki podskup skup R uređeih -torki relih brojev, kžemo d je f rel
(Microsoft Word - VI\212ESTRUKI INTEGRALI zadaci III deo)
 VIŠESTRUKI INTEGRALI - ZAACI ( III EO) Izčunvnje povšine u vni pimenom dvostukog integl Povšin olsti u vni O može se nći po fomuli: P = dd Pime. Izčunj povšinu ogničenu sledećim linijm: =, =, i =. Njpe
VIŠESTRUKI INTEGRALI - ZAACI ( III EO) Izčunvnje povšine u vni pimenom dvostukog integl Povšin olsti u vni O može se nći po fomuli: P = dd Pime. Izčunj povšinu ogničenu sledećim linijm: =, =, i =. Njpe
07_JS aktuatori.rev8_lr_bn [Compatibility Mode]
![07_JS aktuatori.rev8_lr_bn [Compatibility Mode] 07_JS aktuatori.rev8_lr_bn [Compatibility Mode]](/thumbs/102/153299032.jpg) Podsećnje... Poluprovodničke komponente koje se koriste u energetskim pretvrčim SW-kontrolisni prekidčki element (trnzistor ili tiristor) D-diod L-induktivnost C-kpcitivnost F1,F2-zštitni elementi (ultr
Podsećnje... Poluprovodničke komponente koje se koriste u energetskim pretvrčim SW-kontrolisni prekidčki element (trnzistor ili tiristor) D-diod L-induktivnost C-kpcitivnost F1,F2-zštitni elementi (ultr
Problem površine - odredeni integral Matematika 2 Erna Begović Kovač, Literatura: I. Gusić, Lekcije iz Matematike 2
 Problem površine - odredeni integrl Mtemtik 2 Ern Begović Kovč, 2019. Litertur: I. Gusić, Lekcije iz Mtemtike 2 http://mtemtik.fkit.hr Uvod Formule z površinu geometrijskih likov omedenih dužinm (rvnim
Problem površine - odredeni integrl Mtemtik 2 Ern Begović Kovč, 2019. Litertur: I. Gusić, Lekcije iz Mtemtike 2 http://mtemtik.fkit.hr Uvod Formule z površinu geometrijskih likov omedenih dužinm (rvnim
РЕПУБЛИКА СРБИЈА МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА СРПСКО ХЕМИЈСКО ДРУШТВО РЕПУБЛИЧКО ТАКМИЧЕЊЕ ИЗ ХЕМИЈЕ Лесковац, 31. мај и 1. јун
 РЕПУБЛИКА СРБИЈА МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА СРПСКО ХЕМИЈСКО ДРУШТВО РЕПУБЛИЧКО ТАКМИЧЕЊЕ ИЗ ХЕМИЈЕ Лесковац, 31. мај и 1. јун 2014. године ТЕСТ ЗНАЊА ЗА VII РАЗРЕД Шифра ученика
РЕПУБЛИКА СРБИЈА МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА СРПСКО ХЕМИЈСКО ДРУШТВО РЕПУБЛИЧКО ТАКМИЧЕЊЕ ИЗ ХЕМИЈЕ Лесковац, 31. мај и 1. јун 2014. године ТЕСТ ЗНАЊА ЗА VII РАЗРЕД Шифра ученика
Nastavna cjelina: 6. Sukladnost i sličnost Nastavne jedinice: -SUKLADNOST DUŽIN I KUTOVA -SUKLADNOST TROKUTA -SIMETRALA DUŽINE, KUTA I SREDNJICA TROKU
 TEORIJA IZ SUKLADNOST DUŽINA I KUTOVA SUKLADNOST TROKUTA SIMETRALA DUŽINE, KUTA I SREDNJICA TROKUTA ČETIRI KARAKTERISTIČNE TOČKE TROKUTA PROPORCIONALNOST DUŽINA SLIČNOST TROKUTA 6.1. SUKLADNOST DUŽINA
TEORIJA IZ SUKLADNOST DUŽINA I KUTOVA SUKLADNOST TROKUTA SIMETRALA DUŽINE, KUTA I SREDNJICA TROKUTA ČETIRI KARAKTERISTIČNE TOČKE TROKUTA PROPORCIONALNOST DUŽINA SLIČNOST TROKUTA 6.1. SUKLADNOST DUŽINA
DECA MIG/ MAG Naziv : aparat za zav. STARTWIN 180E Bar- kod : Cena : 48, šifra: D aparat za MIG- MAG zavarivanj
 DECA MIG/ MAG 07.2016. Naziv : aparat za zav. STARTWIN 180E Bar- kod : 8011399023435 Cena : 48,985.00 - šifra: D253300 - aparat za MIG- MAG zavarivanje žicom kao i zavarivanje bez gasa uz korišćenje samozaštitne
DECA MIG/ MAG 07.2016. Naziv : aparat za zav. STARTWIN 180E Bar- kod : 8011399023435 Cena : 48,985.00 - šifra: D253300 - aparat za MIG- MAG zavarivanje žicom kao i zavarivanje bez gasa uz korišćenje samozaštitne
Microsoft PowerPoint - IS_G_predavanja_ [Compatibility Mode]
![Microsoft PowerPoint - IS_G_predavanja_ [Compatibility Mode] Microsoft PowerPoint - IS_G_predavanja_ [Compatibility Mode]](/thumbs/102/153298922.jpg) Dva pristupa u analiziranu kretana materiala: 1. Statistički pristup material se tretira kao skup molekula makroskopski fenomeni se obašnavau kao posledica molekularne aktivnosti računane primenom zakona
Dva pristupa u analiziranu kretana materiala: 1. Statistički pristup material se tretira kao skup molekula makroskopski fenomeni se obašnavau kao posledica molekularne aktivnosti računane primenom zakona
Microsoft Word - Elektrijada_V2_2014_final.doc
 I област. У колу сталне струје са слике када је и = V, амперметар показује I =. Одредити показивање амперметра I када је = 3V и = 4,5V. Решење: а) I = ) I =,5 c) I =,5 d) I = 7,5 3 3 Слика. I област. Дата
I област. У колу сталне струје са слике када је и = V, амперметар показује I =. Одредити показивање амперметра I када је = 3V и = 4,5V. Решење: а) I = ) I =,5 c) I =,5 d) I = 7,5 3 3 Слика. I област. Дата
Microsoft Word - FINALNO.doc
 Ako pronñeš cestu ez preprek, zpitj se d li t cest igdje vodi. Projektn nstv Osnovn škol Ivn Gundulić DUBROVNIK MEMENTO (mtemtik) Plnirli smo: Nprviti pregled elementrnih sdržj iz mtemtike s primjerim
Ako pronñeš cestu ez preprek, zpitj se d li t cest igdje vodi. Projektn nstv Osnovn škol Ivn Gundulić DUBROVNIK MEMENTO (mtemtik) Plnirli smo: Nprviti pregled elementrnih sdržj iz mtemtike s primjerim
1_Elektricna_struja_02.03
 Elektrostatika i električna struja Tehnička fizika 2 01-08/03/19 Tehnološki fakultet Prisustvo na predavanjima 5 bod Laboratorijske vježbe 10 bod Test zadaci 1 10 bod Test zadaci 2 10 bod Test teorija
Elektrostatika i električna struja Tehnička fizika 2 01-08/03/19 Tehnološki fakultet Prisustvo na predavanjima 5 bod Laboratorijske vježbe 10 bod Test zadaci 1 10 bod Test zadaci 2 10 bod Test teorija
4.1 The Concepts of Force and Mass
 Električna potencijalna energija i potencijal FIZIKA PSS-GRAD 20. prosinca 2017. 19.1 Potencijalna energija W AB = m g h B m g h A = m g Δ h W AB = E p B E p A = Δ E p (a na lo p gi ja onav l s gr janj
Električna potencijalna energija i potencijal FIZIKA PSS-GRAD 20. prosinca 2017. 19.1 Potencijalna energija W AB = m g h B m g h A = m g Δ h W AB = E p B E p A = Δ E p (a na lo p gi ja onav l s gr janj
OKFH2-10
 KOLOIDI DISPERZNI SISTEMI Disperzni sistemi sistemi u kojima je jedna ili više supstancija (disperzna faza) u većoj ili manjoj meri usitnjena i ravnomerno raspoređena u okružujućoj sredini (disperzno sredstvo).
KOLOIDI DISPERZNI SISTEMI Disperzni sistemi sistemi u kojima je jedna ili više supstancija (disperzna faza) u većoj ili manjoj meri usitnjena i ravnomerno raspoređena u okružujućoj sredini (disperzno sredstvo).
RITAM FORMS POSLOVNI PROCESI RAD S JOPPD OBRASCEM Stranica 1 od 10 Rad s JOPPD obrascem 1. Opće ito Novi obrazac JOPPD Izmjene kod gla
 Stranica 1 od 10 Rad s JOPPD obrascem 1. Opće ito... 1 2. Novi obrazac JOPPD... 3 3. Izmjene kod glavne blagajne... 7 4. Izmjene kod doprinosa... 7 5. Iz je e kod predložaka vir a a... 9 6. Iz je e kod
Stranica 1 od 10 Rad s JOPPD obrascem 1. Opće ito... 1 2. Novi obrazac JOPPD... 3 3. Izmjene kod glavne blagajne... 7 4. Izmjene kod doprinosa... 7 5. Iz je e kod predložaka vir a a... 9 6. Iz je e kod
Microsoft Word - PRAVILNIK O GV AK AM cir.doc
 На основу чл. 38.став 1. и чл. 47.став 3. Закона о заштити ваздуха («Службени гласник Републике Српске», број: 53/02) И члана 58. Закона о министарствима («Сл. гласник Републике Српске», бр. 70/02) министар
На основу чл. 38.став 1. и чл. 47.став 3. Закона о заштити ваздуха («Службени гласник Републике Српске», број: 53/02) И члана 58. Закона о министарствима («Сл. гласник Републике Српске», бр. 70/02) министар
Microsoft Word - INTEGRALI ZADACI.doc
 INTEGRALI ZADAI ( II DEO) INTEGRAIJA POMOĆU SMENE Ako uvedemo smenu = g( ) ond je d= g`( ) i počeni inegrl f ( ) d posje: f ( ) d= f ( g( )) g`( ) Z poček evo jednog sve: z smenu biri izrz čiji je izvod
INTEGRALI ZADAI ( II DEO) INTEGRAIJA POMOĆU SMENE Ako uvedemo smenu = g( ) ond je d= g`( ) i počeni inegrl f ( ) d posje: f ( ) d= f ( g( )) g`( ) Z poček evo jednog sve: z smenu biri izrz čiji je izvod
Microsoft PowerPoint - IS_G_predavanja_ [Compatibility Mode]
![Microsoft PowerPoint - IS_G_predavanja_ [Compatibility Mode] Microsoft PowerPoint - IS_G_predavanja_ [Compatibility Mode]](/thumbs/102/155452201.jpg) Rzvoj mtod u 940-, 960-tim (Boing) (https://www.simscl.com/blog/05//75-yrs-of-th-finitlmnt-mthod-fm/) U počtku prvnstvno z sttičku nlizu mhnik čvrstih tijl, li dns i z dinmičku, prnos toplot, tčnj fluid,...
Rzvoj mtod u 940-, 960-tim (Boing) (https://www.simscl.com/blog/05//75-yrs-of-th-finitlmnt-mthod-fm/) U počtku prvnstvno z sttičku nlizu mhnik čvrstih tijl, li dns i z dinmičku, prnos toplot, tčnj fluid,...
Slide 1
 TEHNOLOŠKE OPERACIJE Predavanje Agregatna stanja - faze Osobine atoma i molekula http://hr.wikipedia.org/wiki/datoteka:water-elpot-transparent-3d-balls.png Fizičke veličine: pritisak i temperatura čvrsto
TEHNOLOŠKE OPERACIJE Predavanje Agregatna stanja - faze Osobine atoma i molekula http://hr.wikipedia.org/wiki/datoteka:water-elpot-transparent-3d-balls.png Fizičke veličine: pritisak i temperatura čvrsto
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Valentina Zemlić LAPLACEOVA TRANSFORMACIJA Diplomski rad Voditelj rada: do
 SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Vlentin Zemlić LAPLACEOVA TRANSFORMACIJA Diplomski rd Voditelj rd: doc. dr. sc. Mj Resmn Zgreb, studeni 217. Ovj diplomski rd
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Vlentin Zemlić LAPLACEOVA TRANSFORMACIJA Diplomski rd Voditelj rd: doc. dr. sc. Mj Resmn Zgreb, studeni 217. Ovj diplomski rd
ИСПИТНА ПИТАЊА ЗА ПРВИ КОЛОКВИЈУМ 1. Шта проучава биофизика и навести бар 3 области биофизике 2. Основне физичке величине и њихове јединице 3. Појам м
 ИСПИТНА ПИТАЊА ЗА ПРВИ КОЛОКВИЈУМ 1. Шта проучава биофизика и навести бар 3 области биофизике 2. Основне физичке величине и њихове јединице 3. Појам материјалне тачке 4. Појам механичког система 5. Појам
ИСПИТНА ПИТАЊА ЗА ПРВИ КОЛОКВИЈУМ 1. Шта проучава биофизика и навести бар 3 области биофизике 2. Основне физичке величине и њихове јединице 3. Појам материјалне тачке 4. Појам механичког система 5. Појам
STATIKA GRAĐEVNIH KONSTRUKCIJA 273 smatra zamišljeni pomak konstrukcije kojim se ona od polaznoga dovodi u neki identični položaj, što se naziva prekl
 STATIKA GRAĐEVNIH KONSTRUKCIJA 273 smatra zamišljeni pomak konstrukcije kojim se ona od polaznoga dovodi u neki identični položaj, što se naziva preklapanjem. Preklapanje se ne odnosi samo na geom etrijske,
STATIKA GRAĐEVNIH KONSTRUKCIJA 273 smatra zamišljeni pomak konstrukcije kojim se ona od polaznoga dovodi u neki identični položaj, što se naziva preklapanjem. Preklapanje se ne odnosi samo na geom etrijske,
28. фебруар године СЛУЖБЕНИ ГЛАСНИК ОПШТИНЕ АРИЉЕ Број 6 Ариље, 28. фебруар године Година MMXIX Број 6 САДРЖАЈ 1. Одлука
 www.arilje.org.rs Ариље, 28. фебрур 2019. године Годин MMXIX Број 6 САДРЖАЈ 1. Одлук о рсписивњу јвног оглс з двње у зкуп и н коришћење пољопривредног земљишт у држвној својини у општини Ариље...2 Н основу
www.arilje.org.rs Ариље, 28. фебрур 2019. године Годин MMXIX Број 6 САДРЖАЈ 1. Одлук о рсписивњу јвног оглс з двње у зкуп и н коришћење пољопривредног земљишт у држвној својини у општини Ариље...2 Н основу
Naknade za poslove Centra za vinogradarstvo, vinarstvo i uljarstvo koje su propisane pravilnikom Redni broj NAZIV PROPISA broj Narodnih Novina 1. Prav
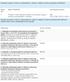 Naknade za poslove Centra za vinogradarstvo, vinarstvo i uljarstvo koje su propisane pravilnikom Redni broj NAZIV PROPISA broj Narodnih Novina 1. Pravilnik o visini naknade troškova za obavljanje usluga
Naknade za poslove Centra za vinogradarstvo, vinarstvo i uljarstvo koje su propisane pravilnikom Redni broj NAZIV PROPISA broj Narodnih Novina 1. Pravilnik o visini naknade troškova za obavljanje usluga
Republika Hrvatska - Ministarstvo znanosti, obrazovanja i sporta Agencija za odgoj i obrazovanje - Hrvatsko kemijsko društvo ŠKOLSKO NATJECANJE IZ KEM
 Republika Hrvatska - Ministarstvo znanosti, obrazovanja i sporta Agencija za odgoj i obrazovanje - Hrvatsko kemijsko društvo ŠKOLSKO NATJECANJE IZ KEMIJE učeni(ka)ca osnovnih i srednjih škola 2013. PISANA
Republika Hrvatska - Ministarstvo znanosti, obrazovanja i sporta Agencija za odgoj i obrazovanje - Hrvatsko kemijsko društvo ŠKOLSKO NATJECANJE IZ KEMIJE učeni(ka)ca osnovnih i srednjih škola 2013. PISANA
Microsoft PowerPoint - IR-Raman1 [Compatibility Mode]
![Microsoft PowerPoint - IR-Raman1 [Compatibility Mode] Microsoft PowerPoint - IR-Raman1 [Compatibility Mode]](/thumbs/101/149990971.jpg) Spektar elektromagnetnoga t zračenja 10 5 10 3 10 1 10-1 10-3 10-5 10-7 E(kJ/mol) 10-6 10-4 10-2 1 10 2 10 4 10-8,cm X UV zrake zrake prijelazi elektrona IR mikrovalovi radiovalovi vibracije rotacije prijelazi
Spektar elektromagnetnoga t zračenja 10 5 10 3 10 1 10-1 10-3 10-5 10-7 E(kJ/mol) 10-6 10-4 10-2 1 10 2 10 4 10-8,cm X UV zrake zrake prijelazi elektrona IR mikrovalovi radiovalovi vibracije rotacije prijelazi
Republika Hrvatska - Ministarstvo znanosti, obrazovanja i športa
 Republika Hrvatska - Ministarstvo znanosti, obrazovanja i športa Agencija za odgoj i obrazovanje - Hrvatsko kemijsko društvo ŠKOLSKO NATJECANJE IZ KEMIJE učeni(ka)ca osnovnih i srednjih škola 2011. PISANA
Republika Hrvatska - Ministarstvo znanosti, obrazovanja i športa Agencija za odgoj i obrazovanje - Hrvatsko kemijsko društvo ŠKOLSKO NATJECANJE IZ KEMIJE učeni(ka)ca osnovnih i srednjih škola 2011. PISANA
Министарство просвете, науке и технолошког развоја ОКРУЖНО ТАКМИЧЕЊЕ ИЗ ХЕМИЈЕ 22. април године ТЕСТ ЗА 8. РАЗРЕД Шифра ученика Српско хемијско
 Министарство просвете, науке и технолошког развоја ОКРУЖНО ТАКМИЧЕЊЕ ИЗ ХЕМИЈЕ 22. април 2018. године ТЕСТ ЗА 8. РАЗРЕД Шифра ученика Српско хемијско друштво (три слова и три броја) УПИШИ Х ПОРЕД НАВЕДЕНЕ
Министарство просвете, науке и технолошког развоја ОКРУЖНО ТАКМИЧЕЊЕ ИЗ ХЕМИЈЕ 22. април 2018. године ТЕСТ ЗА 8. РАЗРЕД Шифра ученика Српско хемијско друштво (три слова и три броја) УПИШИ Х ПОРЕД НАВЕДЕНЕ
Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]
![Microsoft PowerPoint - 03-Slozenost [Compatibility Mode] Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]](/thumbs/102/154806426.jpg) Сложеност алгоритама (Програмирање 2, глава 3, глава 4-4.3) Проблем: класа задатака истог типа Велики број различитих (коректних) алгоритама Величина (димензија) проблема нпр. количина података које треба
Сложеност алгоритама (Програмирање 2, глава 3, глава 4-4.3) Проблем: класа задатака истог типа Велики број различитих (коректних) алгоритама Величина (димензија) проблема нпр. количина података које треба
Slide 1
 Dvadeset četvrto predavanje 1 CILJEVI PREDAVANJA Pojačan efekat staklene bašte H 2 O i CO 2 kao apsorberi radijacije sa Zemlje radijaciono forsiranje Posledice globalnog zagrevanja Izvori i potrošnja gasova
Dvadeset četvrto predavanje 1 CILJEVI PREDAVANJA Pojačan efekat staklene bašte H 2 O i CO 2 kao apsorberi radijacije sa Zemlje radijaciono forsiranje Posledice globalnog zagrevanja Izvori i potrošnja gasova
Microsoft Word - Test 2009 I.doc
 Ime i prezime (ŠTAMPANIM SLOVIMA!!!) jedinstveni matični broj građana (prepisati iz lične karte) broj prijave Test za prijemni ispit iz hemije 1. Hemijska promena je: a) rastvaranje NaCl b) sublimacija
Ime i prezime (ŠTAMPANIM SLOVIMA!!!) jedinstveni matični broj građana (prepisati iz lične karte) broj prijave Test za prijemni ispit iz hemije 1. Hemijska promena je: a) rastvaranje NaCl b) sublimacija
Mate_Izvodi [Compatibility Mode]
![Mate_Izvodi [Compatibility Mode] Mate_Izvodi [Compatibility Mode]](/thumbs/102/155170958.jpg) ИЗВОДИ ФУНКЦИЈЕ ИЗВОДИ ФУНКЦИЈЕ Нека тачке Мо и М чине једну тетиву функције. Нека се тачка М почне приближавати тачки Мо, тј. нека Тачка М постаје тачка Мо, а тетива постаје тангента функције у тачки
ИЗВОДИ ФУНКЦИЈЕ ИЗВОДИ ФУНКЦИЈЕ Нека тачке Мо и М чине једну тетиву функције. Нека се тачка М почне приближавати тачки Мо, тј. нека Тачка М постаје тачка Мо, а тетива постаје тангента функције у тачки
MLADI NADARENI MATEMATIČARI Marin Getaldic Uvod u nejednakosti Nejednakosti su područje koje je u velikoj mjeri zastupljeno na matematički
 MLADI NADARENI MATEMATIČARI Mri Getldic Uvod u ejedkosti..05. Nejedkosti su područje koje je u velikoj mjeri zstupljeo mtemtičkim tjecjim, li se u sredjoškolskom grdivu jedv spomije. Tkvi zdtci mogu stvrti
MLADI NADARENI MATEMATIČARI Mri Getldic Uvod u ejedkosti..05. Nejedkosti su područje koje je u velikoj mjeri zstupljeo mtemtičkim tjecjim, li se u sredjoškolskom grdivu jedv spomije. Tkvi zdtci mogu stvrti
Kvadrupolni maseni analizator, princip i primena u kvali/kvanti hromatografiji
 Kvadrupolni maseni analizator, princip i primena u kvali/kvanti hromatografiji doc dr Nenad Vuković, Institut za hemiju, Prirodno-matematički fakultet u Kragujevcu JONIZACIJA ELEKTRONSKIM UDAROM Joni u
Kvadrupolni maseni analizator, princip i primena u kvali/kvanti hromatografiji doc dr Nenad Vuković, Institut za hemiju, Prirodno-matematički fakultet u Kragujevcu JONIZACIJA ELEKTRONSKIM UDAROM Joni u
Microsoft PowerPoint - fizika 9-oscilacije
 Предиспитне обавезе Шема прикупљања поена - измене Активност у току предавања = 5 поена (са више од 3 одсуствовања са предавања се не могу добити) Лабораторијске вежбе = 10 поена обавезни сви поени односно
Предиспитне обавезе Шема прикупљања поена - измене Активност у току предавања = 5 поена (са више од 3 одсуствовања са предавања се не могу добити) Лабораторијске вежбе = 10 поена обавезни сви поени односно
Numeričke metode u fizici 1, Projektni zadataci 2018./ Za sustav običnih diferencijalnih jednadžbi, koje opisuju kretanje populacije dviju vrs
 Numeričke metode u fizici, Projektni zadataci 8./9.. Za sustav običnih diferencijalnih jednadžbi, koje opisuju kretanje populacije dviju vrsta životinja koje se nadmeću za istu hranu, dx ( dt = x x ) xy
Numeričke metode u fizici, Projektni zadataci 8./9.. Za sustav običnih diferencijalnih jednadžbi, koje opisuju kretanje populacije dviju vrsta životinja koje se nadmeću za istu hranu, dx ( dt = x x ) xy
Microsoft PowerPoint - fizika 7-fluidi-dinamika-2014
 ФИЗИКА 2014. Понедељак, 23. новембар 2014. године Статика флуида Густина и притисак флуида Промена притиска са дубином флуида Паскалов принцип Калибрација, апсолутни притисак и мерење притиска Архимедов
ФИЗИКА 2014. Понедељак, 23. новембар 2014. године Статика флуида Густина и притисак флуида Промена притиска са дубином флуида Паскалов принцип Калибрација, апсолутни притисак и мерење притиска Архимедов
STRELIČARSKI SAVEZ SRBIJE, BEOGRAD REVIZIJA SAGLASNOSTI Izveštaj revizora o ispunjenju ugovorenih obaveza Redovnog programa za godinu Konsultant
 STRELIČARSKI SAVEZ SRBIJE, BEOGRAD Izveštaj revizora o ispunjenju ugovorenih obaveza Redovnog programa za 2017. godinu Konsultant - Revizija doo REVIZIJA POREZI RAČUNOVODSTVO KONSALTING www.konsrev.rs
STRELIČARSKI SAVEZ SRBIJE, BEOGRAD Izveštaj revizora o ispunjenju ugovorenih obaveza Redovnog programa za 2017. godinu Konsultant - Revizija doo REVIZIJA POREZI RAČUNOVODSTVO KONSALTING www.konsrev.rs
IPPC zahtev[1] [Compatibility Mode]
![IPPC zahtev[1] [Compatibility Mode] IPPC zahtev[1] [Compatibility Mode]](/thumbs/102/154561259.jpg) ПРИМЕНА IPPC ДИРЕКТИВЕ У СРБИЈИ ЗАХТЕВ ЗА ИЗДАВАЊЕ ИНТЕГРИСАНЕ ДОЗВОЛЕ qзакон о интегрисаном спречавању и контроли загађивања животне средине (Сл. Гласник РС, број 135/2004) Уређује услове и поступак издавања
ПРИМЕНА IPPC ДИРЕКТИВЕ У СРБИЈИ ЗАХТЕВ ЗА ИЗДАВАЊЕ ИНТЕГРИСАНЕ ДОЗВОЛЕ qзакон о интегрисаном спречавању и контроли загађивања животне средине (Сл. Гласник РС, број 135/2004) Уређује услове и поступак издавања
Otpornost materijala
 Prethodno predavanje Statika je deo mehanike koji se bavi: OdreĎivanjem uslova ravnoteţe krutih tela koja su izloţena mehaničkom dejstvu Slaganjem sila i svoďenjem sistema na prostiji Korišćeni i definisani
Prethodno predavanje Statika je deo mehanike koji se bavi: OdreĎivanjem uslova ravnoteţe krutih tela koja su izloţena mehaničkom dejstvu Slaganjem sila i svoďenjem sistema na prostiji Korišćeni i definisani
REPUBLIKA HRVATSKA BJELOVARSKO BILOGORSKA ŽUPANIJA GRAD DARUVAR GRADONAČELNIK KLASA: /19-01/01 URBROJ: 2111/ / Daruvar, 02. siječnj
 REPUBLIKA HRVATSKA BELOVARSKO BILOGORSKA ŽUPANIA GRAD DARUVAR GRADONAČELNIK KLASA: 406-09/19-01/01 URBRO: 2111/01-02-02/1-19-1 Druvr, 02. siječnj 2019. g. N temelju člnk 28. Zkon o jvnoj nbvi (NN RH, broj
REPUBLIKA HRVATSKA BELOVARSKO BILOGORSKA ŽUPANIA GRAD DARUVAR GRADONAČELNIK KLASA: 406-09/19-01/01 URBRO: 2111/01-02-02/1-19-1 Druvr, 02. siječnj 2019. g. N temelju člnk 28. Zkon o jvnoj nbvi (NN RH, broj
PowerPoint Presentation
 Prečišćavanje otpadnih gasova Pregled SISTEMI ZA PREČIŠĆAVANJE OTPADNIH GASOVA SISTEMI ZA UKLANJANJE ČESTICA SISTEMI ZA UKLANJANJE GASOVITIH POLUTANATA 10 Emisija u svetu (Mt/god) CO VOCs SOx NOx ČESTICE
Prečišćavanje otpadnih gasova Pregled SISTEMI ZA PREČIŠĆAVANJE OTPADNIH GASOVA SISTEMI ZA UKLANJANJE ČESTICA SISTEMI ZA UKLANJANJE GASOVITIH POLUTANATA 10 Emisija u svetu (Mt/god) CO VOCs SOx NOx ČESTICE
UNIVERZITET U TUZLI Filozofski fakultet Broj: 02/ /17 Tuzla, godine Na osnovu člana 122. Statuta Univerziteta u Tuzli, a u vezi sa
 Studijski program Komunikologija Nakon što je prijavu kandidata Azre Musić odbacilo kao nepotpunu Naučno-nastavno vijeće utvrďuje slijedeću U prvu godinu drugog studija u akademskoj 2017/2018. godini u
Studijski program Komunikologija Nakon što je prijavu kandidata Azre Musić odbacilo kao nepotpunu Naučno-nastavno vijeće utvrďuje slijedeću U prvu godinu drugog studija u akademskoj 2017/2018. godini u
T E O R I J A G R A F O V A Do sada smo koristili grafove za predstavljanje relacija. Međutim, teorija grafova je samostalni i važan deo matematike. G
 T E O R I J A G R A F O V A Do sd smo koristili grfove z predstvljnje relij. Međutim, teorij grfov je smostlni i vžn deo mtemtike. Grfovi su poseno znimljivi jer pomoću njih možemo modelovti složene proleme
T E O R I J A G R A F O V A Do sd smo koristili grfove z predstvljnje relij. Međutim, teorij grfov je smostlni i vžn deo mtemtike. Grfovi su poseno znimljivi jer pomoću njih možemo modelovti složene proleme
Одлука о изменама и допуни Одлуке о општим правилима за извршавање инстант трансфера одобрења 1. У Одлуци о општим правилима за извршавање инстант тра
 Одлук о изменм и допуни Одлуке о општим првилим з извршвње инстнт трнсфер одобрењ 1. У Одлуци о општим првилим з извршвње инстнт трнсфер одобрењ ( Службени глсник РС, број 65/18 у дљем тексту: Одлук),
Одлук о изменм и допуни Одлуке о општим првилим з извршвње инстнт трнсфер одобрењ 1. У Одлуци о општим првилим з извршвње инстнт трнсфер одобрењ ( Службени глсник РС, број 65/18 у дљем тексту: Одлук),
