UNIVERZITET U PRIRODNO - MATEMATIČKI NIŠU FAKULTET KOMPRESIJA SLIKA: JPEG I JPEG2000 FORMAT Master rad Student: MLADEN -DOR-DEVIĆ Mentor: Prof. dr MAR
|
|
|
- Kosta Grošelj
- пре 5 година
- Прикази:
Транскрипт
1 UNIVERZITET U PRIRODNO - MATEMATIČKI NIŠU FAKULTET KOMPRESIJA SLIKA: JPEG I JPEG2000 FORMAT Master rad Student: MLADEN -DOR-DEVIĆ Mentor: Prof. dr MARKO PETKOVIĆ Niš, Oktobar 2017
2 SADRŽAJ SADRŽAJ Sadržaj 1 Predstavljanje slika u računaru Uvod Binarne (1-bitne) slike Monohromatske (8-bitne) slike Kompresija slika Uvod Performanse kompresije Faktor kompresije Mere kompresije JPEG format Uvod Algoritam Modeli boja RGB model YCbCr model Diskretna kosinusna transformacija Kvantizacija Kodiranje Dekompresija Eksperimentalni rezultati JPEG2000 format Uvod Pretprocesiranje Podela na blokove DC pomeranje Transformacija multi-komponenti Reverzibilna transformacija boja Ireverzibilna transformacija boja Kompresija Vejvlet transformacija Diskretna vejvlet transformacija Multi-rezoluciona analiza
3 SADRŽAJ SADRŽAJ Filteri i piramidalni algoritam Dvodimenzionalna diskretna vejvlet transformacija Kompresija sa gubicima korišćenjem diskretne vejvlet transformacije Kompresija bez gubitaka korišćenjem reverzibilne vejvlet transformacije Procesiranje ivica blokova Kvantizacija Kodiranje Zaključak 52 2
4 1 PREDSTAVLJANJE SLIKA U RAČUNARU 1 Predstavljanje slika u računaru 1.1 Uvod Slika predstavlja reprezentaciju objekta, osobe ili scene dobijene pomoću nekog optičkog ured aja kao što je ogledalo, sočivo ili kamera. Ova reprezentacija je dvodimenzionalna (2D), iako predstavlja neku projekciju iz realnog sveta - trodimenzionalni (3D) objekat ili scenu. Digitalna slika je numerička reprezentacija dvodimenzionalne slike pomoću konačnog broja tačaka koje nazivamo pikselima. Svaki piksel je predstavljen pomoću jedne ili više numeričkih vrednosti. Digitalna slika se predstavlja dvodimenzionalnom realnom matricom. Sa f(x, y) ćemo označavati sliku dimenzije M N, gde x predstavlja broj vrste (0,..., M 1), a y broj kolone (0,..., N 1): f(0, 0) f(0, 1)... f(0, N 1) f(1, 0) f(1, 1)... f(1, N 1) f(x, y) = (1.1)... f(m 1, 0) f(m 1, 1)... f(m 1, N 1) Vrednost dvodimenzionalne funkcije f(x, y) u pikselu sa koordinatama (x 0, y 0 ) označava se sa f(x 0, y 0 ) i naziva se intenzitet slike u tom pikselu. Maksimalne i minimalne vrednosti intenziteta zavise od tipa slike i konvencije. 1.2 Binarne (1-bitne) slike Binarne slike su kodirane kao matrica i koristi se 1 bit po pikselu gde 0 označava crnu a 1 belu boju. Glavna prednost ovakve reprezentacije je mala memorija potrebna sa pamćenje slika. To su uglavnom slike koje sadrže tekst ili jednostavne grafičke prikaze. Slika 1.1. predstavlja binarnu sliku (rezultat izdvajanja ivica) i označenu oblast dimenzije Monohromatske (8-bitne) slike Monohromatske slike takod e su kodirane kao matrice i to sa 8 bita po pikselu. Vrednost piksela 0 označava crnu, a vrednost 255 belu boju. Sve vrednosti izmed u predstavljaju odred enu nijansu sive boje. 3
5 2 KOMPRESIJA SLIKA Slika 1.1: Binarna slika 2 Kompresija slika 2.1 Uvod Slika 1.2: Monohromatska slika Slike se u digitalnom obliku mogu predstaviti na više različitih načina, a jedan od najprostijih je da se vrednosti svih piksela čuvaju u fajlu na osnovu neke konvencije (npr. polazeći od piksela koji se nalazi u gornjem levom uglu slike). Posledica korišćenja ovakve reprezentacije slika je veliki memorijski prostor koji je potreban za njihovo čuvanje. Da bi se smanjio memorijski prostor za čuvanje slika koriste se tehnike kompresije slika. Ove tehnike takod e smanjuju troškove komunikacije prilikom prenosa velike količine podataka. Osim ovih dobrih osobina, postoje i negativne strane kompresije. Kada se pristupa nekom podatku 4
6 2.1 Uvod 2 KOMPRESIJA SLIKA kod kompresovanih baza podataka, ponekad je potrebno dekompresovati celu bazu da bismo dosli do željenog podatka. Takva situacija se javlja kod baza čiji se podaci red e menjaju (na primer, u statistici). Takod e, ukoliko dod e do greške na jednom bitu kompresovanog koda, dekoder može preostale bitove da pogrešno interpretira čime se dolazi do loših podataka. U mnogim sistemima dodatna kompleksnost prilikom dodavanja procesa kompresije može značajno da poveća troškove sistema i umanji njegovu efikasnost. Tehnike kompresije slika su danas prisutne u popularnim aplikacijama i ured ajima kao što su DVD plejeri ili digitalne kamere. Dobri algoritmi kompresije slika su u mogućnosti da sliku u velikoj meri kompresuju, a da degradacija slike bude minimalna što se tiče vizuelnog kvaliteta. U apstraktnom smislu, kompresiju podataka možemo definisati kao metod koji od ulaznih podataka D generiše kraću reprezentaciju tih podataka c(d), sa manjim brojem bitova u odnosu na D. Obrnuti proces se naziva dekompresija i u tom procesu se od kompresovanih podataka c(d) generišu ili rekonstruišu podaci D (Slika 2.1). Ponekad se sistemi za kompresiju i dekompresiju zajednički zovu CODEC (COmpression - DECompression). Metodi kompresije mogu biti: Slika 2.1: CODEC sa gubicima (lossy) - kada su rezultujući podaci D aproksimacija originalnih podataka D, bez gubitaka (lossless) - kada su rezultujući podaci D u potpunosti identični u odnosu na originalne podatke D. Kod slika, kompresija sa gubicima koristi činjenicu da ljudsko oko teško razlikuje približno identične boje. U mnogim situacijama je mali gubitak podataka prihvatljiv kad sa uzme u obzir veća kompresija. Kompresija sa gubicima može imati primenu kod klasičnih fotografija, dok se kompresija bez gubitaka koristi kod slika u medicini, tehničkih crteža. 5
7 2.2 Performanse kompresije 2 KOMPRESIJA SLIKA 2.2 Performanse kompresije Tipični model za kompresiju podataka može da se opiše sledećim koracima: Odbacivanje redundantnih podataka Redukcija entropije Kodiranje entropije Redundansa u podacima može da se javi u više oblika. Na primer, susedni pikseli na slici su med usobno korelisani. Pod korelacijom se podrazumeva da su vrednosti susednih piksela veoma slične, osim na primer, u delovima slike koji sadrže naglu promenu boje. Kompozicija reči u prirodnom govoru prati isti model na osnovu odred ene gramatike, a takod e se izmed u reči prave pauze. U ovim slučajevima redundansa u podacima može da se smanji kako bi se postigla kompresija. Smanjenje redundanse u podacima obično se postiže transformacijom podataka iz jedne reprezentaciju u drugu. Popularne tehnike smanjivanja redundanse su predikcija uzorka podataka na osnovu nekog modela, transformacija iz prostornog u frekventni domen kao kod diskretne kosinusne transformacije (DCT), dekompozicija originalnog skupa podataka u različite podgrupe kao kod diskretne vejvlet transformacije (DWT). Kod kompresije bez gubitaka ovaj korak je kompletno reverzibilan. Sledeći korak kod kompresije sa gubicima je da se smanji entropija kako bi bilo potrebno manje bitova za memorisanje ili prenos podataka. To se postiže odbacivanjem manje značajnih informacija na osnovu nekih kriterijuma. Proces nije reverzibilan jer nije moguće potpuno povratiti izgubljene podatke pomoću inverznog procesa. Ovaj korak se primenjuje kod kompresije sa gubicima i završava se obično primenom neke od tehnika kvantizacije. Nakon toga, kvantizirani koeficijenti se kodiraju. S obzirom da je entropija kvantiziranih podataka manja od entropije originalnih podataka, potrebno je manje bitova za njihovo predstavljanje čime je postignuta kompresija. Osnovni problem kompresije slika je da se smanji količina podataka (bitova) koji su potrebni za predstavljanje slike. Matematički gledano, kompresija podataka predstavlja transformaciju (kodiranje) dvodimenzionalnog niza piksela u neki statistički nekorelisani skup podataka. U procesu dekodiranja rekonstruiše se originalna slika (kod kompresije bez gubitaka) ili se dobija aproksimacija originalne slike (kod kompresije sa gubicima). 6
8 2.2 Performanse kompresije 2 KOMPRESIJA SLIKA U teoriji informacija, redundantnost možemo definisati kao razliku broja bitova koji su korišćeni za prenos neke poruke i broja bitova stvarne informacije u toj poruci. Proces kompresije podataka eliminiše neželjenu redundansu. Ako istu informaciju možemo reprezentovati na više načina, onda možemo da kažemo da ona reprezentacija koja zahteva više podataka sadrži redundantne podatke. Da bi razlikovali podatak od informacije posmatrajmo sledeći primer: istu informaciju (broj 4) možemo predstaviti pomoću različitih reprezentacija (u rastućem redosledu u odnosu na broj bitova): Binarni ekvivalent broj 4 (100): 3 bita; Rimski broj IV kodiran pomoću ASCI karaktera za I i V: 16 bitova; Reč quatro što znači četiri na portugalskom jeziku, kodiran takod e pomoću ASCI karaktera: 48 bitova; Nekompresovana binarna (crno-bela) slika dimenzije na kojoj se nalaze četiri bela kvadrata na crnoj pozadini: bitova. Kao i u mnogim drugim sistemima, performanse igraju glavnu ulogu u izboru odred enog algoritma kompresije. Izbor odgovarajućeg algoritma kompresije uglavnom zavisi od potreba same aplikacije: veća ili manja kompresija, subjektivni i objektivni kvalitet rekonstruisanih podataka, složenost algoritma, brzina izvršenja Faktor kompresije Najpopularnija metrika za odred ivanje performansi algoritma kompresije je faktor kompresije. On predstavlja odnos broja bitova originalnih podataka i broja bitova kompresovanih podataka. Postatramo sliku dimenzije za čije je predstavljanje potrebno bajta, ako je za svaki piksel potrebno po jedan bajt. Ako je za predstavljanje ove slike nakon kompresije potrebno 4096 bajta (16 puta manje od originalne), onda faktor kompresije predstavljamo kao 16 : 1. Matematička definicija redundantnosti podataka data je sledećom formulom: R = 1 1 CR gde parametar CR predstavlja faktor kompresije i definiše se kao: (2.2) CR = b 1 b 2 7
9 2.2 Performanse kompresije 2 KOMPRESIJA SLIKA b 1 i b 2 su brojevi bitova u dva različita skupa podataka koji predstavljaju istu informaciju. Formula (2.2) predstavlja relativnu redundansu prvog skupa podataka (b 1 ). Kad je b 2 = b 1, tada je CR = 1 i R = 0, pa možemo reći da prvi skup podataka (b 1 ) ne sadrži redundantne podatke. Kada je b 2 b 1, onda CR i R 1, pa dobijamo visoku redundansu i kao posledicu veliku kompresiju podataka. Konačno, kada je b 2 b 1, CR 0 i R, možemo zaključiti da drugi skup sadrži mnogo više podataka od prvog i ovaj slučaj nije poželjan u procesu kompresije. CR i R uzimaju vrednosti iz intervala [0, + ] i [, 1], respektivno. Faktor kompresije vrednosti 100 (ili 100:1) znači da prvi skup podataka ima 100 jedinica informacije (bitova) za svaku jedinicu informacije drugog (kompresovanog) skupa. Odgovarajuća redundansa (0.99 u ovom slučaju) znači da je 99% podataka redundantno. Jedna varijacija faktora kompresije je prosečan broj bitova po uzorku. Ako je piksela slike kompresovano na 4096 bajta, onda kažemo da je kompresija 0.5 bita po pikselu Mere kompresije Kvalitet kompresije može se predstaviti na osnovu subjektivnih i objektivnih ocena. Najčešće se subjektivna ocena definiše preko prosečne ocene posmatrača (mean observer score - MOS). Postoje različiti statistički načini da se izračuna M OS, a jedan od najprostijih je da se slučajno izabere statistički značajan broj posmatrača koji bi vizuelno ocenili kvalitet kompresije. Na primer, te ocene mogu biti od 1 do 5, pri čemu 5 predstavlja najbolji a 1 najgori kvalitet. Sve ocene se sabiraju a potom dele sa brojem uzoraka (posmatrača) čime se dobija subjektivna ocena kompresije. Oštećenja slike koja su vidljiva nakon dekompresije nazivaju se artifakti kompresije. Ne postoji univerzalno prihvaćena objektivna ocena kvaliteta kompresije, ali najčešće se koristi srednja kvadratna greška (Root Mean Square - RMS). Neka je f(x, y) originalna a f (x, y) rekonstruisana slika. Za sve x i y, greška e(x, y) izmed u f (x, y) i f(x, y) je: e(x, y) = f (x, y) f(x, y) a ukupna greška izmed u slika (dimenzija M N) : E = M 1 N 1 x=0 y=0 [f (x, y) f(x, y)]. 8
10 3 JPEG FORMAT RMS greška (e RMS ) izmed u f (x, y) i f(x, y) se računa na sledeći način: e RMS = 1 M 1 N 1 [f MN (x, y) f(x, y)] 2. (2.3) x=0 y=0 Kod kompresije slika RMS se često predstavlja i preko ekvivalentne recipročne vrednosti - PSNR (Peak Signal to Noise Ratio) definisane sa: P SNR = 10 log 10 (2 B 1) 2 e RMS gde B predstavlja broj bitova po pikselu, pa u slučaju kad je svaki piksel predstavljen sa 8 bitova dobijamo: P SNR = 10 log 10 = 20 log e 10 = 20 log log 10 e RMS RMS erms PSNR se izražava u decibelima (db), što je PSNR vrednost veća, to je rekonstruisana slika bolja u pogledu vizuelnog kvaliteta. Obično dobro rekonstruisane slike imaju vrednost PSNR od 30 db i više. 3 JPEG format 3.1 Uvod Rad na med unarodnim standardima za kompresiju slika počeo je kasnih sedamdesetih godina prošlog veka kada je ogranak Ujedinjenih nacija pod nazivom Consultative Committee of the International Telephone and Telegraph (CCITT) standardizovao algoritme za kompresiju binarnih slika. Od tada, mnoge organizacije su formirale de jure (zakonske) standarde kao što su, na primer, JPEG ili JPEG2000. Sa druge strane, pojedini komercijalno uspešni standardi postali su de facto (masovno korišćeni ali ne i zakonom propisani) standardi poput PDF formata. Standardi za kompresiju slika imaju velike prednosti kao što je lakša razmena slika izmed u različitih ured aja i aplikacija, ponovno korišćenje postojećeg hardvera i softvera za širi skup proizvoda. Za kvalitetnije slike (i crno-bele i u boji) koriste se različiti standardi, naročito oni koji su bazirani na kompresiji sa gubicima. Najpopularniji je JPEG standard 9
11 3.2 Algoritam 3 JPEG FORMAT - algoritam za kodiranje koji koristi diskretne kosinusne transformacije (DCT). Uprkos velikoj popularnosti i prihvaćenosti kod korisnika, odred ena ograničenja originalnog JPEG algoritma u novije vreme dovela su do razvoja dva alternativna standarda: JPEG2000 i JPEGLS (lossless). JPEG standard se definiše u 4 oblika: 1. Sekvencijalni JPEG bez gubitaka - kompresuje sliku u jednom prolazu i rezultujuća slika je replika originalne slike. 2. Sekvencijalni JPEG sa gubicima - kompresuje sliku u jednom prolazu koristeći DCT, rezultujuća slika ne predstavlja repliku već aproksimaciju originalne slike (kompresija sa gubicima). 3. Progresivni JPEG sa gubicima - kompresuje i dekompresuje sliku u više prolaza, pri čemu se sa svakim prolazom povećava kvalitet slike. 4. Hijerarhijski JPEG - Kompresuje sliku u više rezolucija, zbog prikaza na više različitih ured aja. Hijerarhijski i sekvencijalni JPEG bez gubitaka danas imaju vrlo malu ili nikakvu primenu. Ubedljivo najveću primenu ima sekvencijalni JPEG sa gubicima i obično se podrazumeva da se radi o ovom tipu kad se govori o JPEG formatu. Jedna od glavnih mana sekvencijalnog JPEG-a je da svi bitovi moraju biti primljeni i dekodirani kako bi se slika prikazala, što u mnogim aplikacijama nije prihvatljivo. U tim slučajevima se koristi progresivni JPEG, gde se nakon prve iteracije prikazuje slika lošijeg kvaliteta koji se poboljšava sa svakom sledećom iteracijom. 3.2 Algoritam JPEG (Joint Photographic Experts Group) je kao standard objavljen godine. JPEG kodiranje se sastoji iz sledećih koraka: 1. Originalna slika u boji (RGB) se konvertuje u alternativni model boja (YCbCr) i informacija o bojama se deli na uzorke; 2. Slika se deli na blokove dimenzije 8 8; 3. Dvodimenzionalna diskretna kosinusna transformacija (DCT) se primenjuje na svaki blok slike. Dobijaju se 64 vrednosti koje se nazivaju DCT koeficijenti; 10
12 3.3 Modeli boja 3 JPEG FORMAT 4. DCT koeficijenti se kvantiziraju na osnovu tabele kvantizacije. U ovom koraku se uvodi prihvatljivi stepen greške; 5. Na kvantizirane DCT koeficijente si primenjuje cik-cak (zig-zag) funkcija; 6. Dobijene vrednosti se kodiraju u binarne kodne reči pomoću Hafmanovog algoritma. Pri dekodiranju primenjuju se odgovarajući inverzni procesi. Greška koja je uvedena u koraku kvantizacije ne može da se poništi u procesu dekvantizacije. Zbog toga, vrednosti koje dobijemo na izlazu dekvantizera su aproksimacije vrednosti na ulazu u procesu kvantizacije a ne njihove tačne vrednosti. Ukoliko radimo sa monohromatskim (crno-belim) slikama onda je prvi korak u prethodnom algoritmu suvišan. Slika 3.1: JPEG algoritam 3.3 Modeli boja Postoji puno načina da se boje predstave numerički. Sistem za predstavljanje boja se zove model boja. U informatici najkorišćeniji model boja je RGB model. 11
13 3.3 Modeli boja 3 JPEG FORMAT RGB model Kod RGB modela svaki piksel se sastoji od 3 komponente koje predstavljaju intenzitet crvene (R), zelene (G) i plave (B) boje. RGB model se bazira na teoriji da sve boje mogu da se dobiju kombinacijom crvene, zelene i plave boje. U matematici, vrednost svake komponente je obično normalizovana na interval , dok u informatici se te vrednosti predstavljaju celobrojnim vrednostima u nekom opsegu. Ovaj opseg predstavlja broj bitova koji se koristi za predstavljanje jedne komponente (sample precision). Najčešće se koriste 8-bitne vrednosti pa kombinacija tri 8-bitne u 24-bitnu vrednost omogućava 2 24 (16,777,216 - obično se označava kao 16M) kombinacija boja. RGB boje se takod e mogu predstaviti u heksadecimalnoj notaciji sa vrednostima komponenata od 00 (decimalno 0) do F F (decimalno 255). Na taj način bi se, na primer, crvena boja predstavila kao F F Slika 3.2: RGB model: a) Originalna slika; b) R kanal; c) G kanal; d) B kanal. 12
14 3.3 Modeli boja 3 JPEG FORMAT YCbCr model Ovaj model takod e ima 3 komponente i to: 1. Y - predstavlja osvetljenje (brightness) piksela i naziva se još i luminansa (luminance); 2. Cb - predstavlja razliku izmed u komponente plave boje i luminanse; 3. Cr - predstavlja razliku izmed u komponente crvene boje i luminanse. Zbog gustine receptora za osvetljenje i boju u oku, ljudsko oko je osetljivije na promenu osvetljenja (Y komponenta) nego na promenu boja (Cb i Cr komponente). Iz ovih razloga YCbCr model se koristi u digitalnoj televiziji i fotografiji. Slika 3.3: YCbCr model: a) Originalna slika; b) Y kanal; c) Cb kanal; d) Cr kanal. Kod kompresije JPEG formata, RGB model se najpre konvertuje u YCbCr model pomoću sledeće transformacije: 13
15 3.3 Modeli boja 3 JPEG FORMAT Y Cb Cr = R G B Odgovarajuća inverzna transformacija iz YCbCr u RGB model je: R Y 0 G = Cb 128. B Cr 128 Konverzija u YCbCr prostor omogućava veću kompresiju bez nekih gubitaka perceptivnog kvaliteta slike. Kompresija je efikasnija zbog izdvojene informacije o osvetljenju na koje je ljudsko oko osetljivije. Zbog gustine receptora za osvetljenje i boju u oku, ljudi mogu da uoče više detalja sadržanih u osvetljenju (Y komponenta) nego u bojama (Cb i Cr komponente). Iz ovih razloga YCbCr model se koristi u digitalnoj televiziji. Najprostiji način za iskorišćavanje slabije osetljivosti oka na boje je da se koristi manji broj bitova za Cb i Cr kanale. Na primer, ako je slika dimenzije , onda možemo koristiti sve piksele za luminansu (Y) i samo piksela za svaki kanal hrominanse (Cb i Cr). U ovoj reprezentaciji, svaki piksel jednog kanala hrominanse pokriva isti prostor kao 2 2 blok piksela luminanse. Dakle, umesto početnih 12 vrednosti, potrebno je da pamtimo vrednosti 6 piksela za svaki 2 2 blok (4 vrednosti za luminansu i po jedan za oba kanala hrominanse). Ovim smo ostvarili uštedu od 50%, a gubitaka u vidljivom kvalitetu slike gotovo i da nema. Ovakav pristup kod RGB prostora boja nije moguć jer svaka od 3 komponente sadrži informaciju o luminansi, pa bi primena prethodno opisanog procesa dovela do veoma vidljivog gubitka kvaliteta rezultujuće slike. Ovakvo smanjivanje rezolucije kanala hrominanse se naziva daunsemplovanje (downsampling) i JPEG standard dozvoljava upotrebu različitih tipova daunsemplovanja kanala. Kanal luminanse uvek ostaje u punoj rezoluciji (1:1 semplovanje). Obično se oba kanala hrominanse daunsempluju 2:1 horizontalno i 1:1 ili 2:1 vertikalno, što znači da svaki piksel hrominanse pokriva isti prostor kao 2 1, odnosno 2 2 blok piksela luminanse. Ovi procesi daunsemplovanja se označavaju sa 2h1v i 2h2v, redom. Još jedna notacija koja se često koristi je 4:2:2 za 2h1v i 4:2:0 za 2h2v semplovanje. U daljoj kompresiji svaka od komponenata Y, Cb i Cr se posebno procesira na isti način.. 14
16 3.4 Diskretna kosinusna transformacija 3 JPEG FORMAT 3.4 Diskretna kosinusna transformacija Diskretna kosinusna transformacija (DCT) predstavlja osnovu mnogih algoritama kompresije, prvenstveno JPEG formata kod slika i MPEG-1, MPEG-2 i MPEG-4 formata kod video kompresije. S obzirom da je slika dvodimenzionalni signal, za kompresiju se primenjuje dvodimenzionalni DCT. Ova funkcija je separabilna, pa može da se izračuna primenom jednodimenzionalnog DCT-a duž horizontale a potom i vertikale signala. Jednodimenzionalna diskretna kosinusna transformacija (1-D DCT) od N uzoraka je zadata sledećom formulom: za i = 0, 1,..., N 1, gde je: N 1 2 D(i) = N C(i) p(x) cos x=0 (2x + 1)iπ 2N (3.1) C(i) = { 1 2, ako je i = 0 1, ako je i > 0. Funkcija p(x) predstavlja vrednost ulaznog signala na poziciji x, a D(i) je DCT koeficijent za i = 0, 1,..., N 1. Jednodimenzionalna inverzna diskretna kosinusna transformacija (1-D IDCT) se definiše na sličan način: p(x) = N 1 2 C(i)D(i) cos N x=0 (2x + 1)iπ 2N (3.2) za x = 0, 1,..., N 1. Dvodimenzionalna diskretna kosinusna transformacija (2D-DCT) nad N M uzoraka je zadata sledećom formulom: D(i, j) = 2 2 N N 1 M C(i)C(j) x=0 M 1 y=0 p(x, y) cos za i = 0, 1,..., N 1, j = 0, 1,..., M 1 i gde je: { 2 1, ako je u = 0 C(u) = 1, u suprotnom. 15 (2x + 1)iπ 2N cos (2y + 1)jπ 2M (3.3)
17 3.4 Diskretna kosinusna transformacija 3 JPEG FORMAT Ako sliku predstavimo matricom p, onda je p(x, y) je piksel na poziciji (x, y), N M je dimenzija bloka na koji si primenjuje DCT, a D(i, j) je DCT koeficijent za i = 0, 1,..., N 1 i j = 0, 1,..., M 1. Izraz (3.3) je separabilna funkcija jer se može zapisati i kao: M 1 { 2 D(i, j) = M C(j) N 1 2 N C(i) p(x, y) cos y=0 x=0 } (2x + 1)iπ (2y + 1)jπ cos 2N 2M (3.4) Kao rezultat prethodnih zaključivanja, 2-D DCT možemo izračunati u 2 koraka i to najpre računanjem 1D DCT za sve vrste nezavisno pri čemu se dobija D(i, y) gde je: N 1 2 D(i, y) = N C(i) p(x, y) cos x=0 (2x + 1)iπ 2N za i = 0, 1,..., N 1. U drugom koraku se primenjuje 1D DCT na sve kolone D(i, y) pri čemu se dobija D(i, j): M 1 2 D(i, j) = M C(j) D(i, y) cos j=0 (2y + 1)jπ 2M za j = 0, 1,..., M 1. Dvodimenzionalna inverzna kosinusna transformacija 2-D IDCT se dobija na sledeći način: p(x, y) = 2 2 N M N 1 i=0 M 1 j=0 C(i)C(j)D(i, j) cos (2x + 1)iπ 2N cos (2y + 1)jπ 2M (3.5) za x = 0, 1,..., N 1 i y = 0, 1,..., M 1. Ova funkcija je takod e separabilna i može da se izračuna na potpuno inverzan način u odnosu na 2-D DCT. Najpre primenom 1-D IDCT na svaku kolonu ulaznog signala D(i, j). Neka je D(i, y): D(i, y) = M 1 2 C(j)D(i, j) cos M j=0 16 (2y + 1)jπ 2M
18 3.4 Diskretna kosinusna transformacija 3 JPEG FORMAT za j = 0, 1,..., M 1. U drugom koraku se primenjuje 1-D IDCT na sve vrste D(i, y): p(x, y) = N 1 2 C(i)D(i, y) cos N i=0 (2x + 1)iπ 2N za i = 0, 1,..., N 1. Već smo napomenuli da JPEG format koristi blokove dimenzije 8 8 kao standard, pa imamo da je N = M = 8, a x i y uzimaju vrednosti od 0 do 7. Zamenom ovih vrednosti u jednačinu (3.3) dobijamo: D(i, j) = 1 4 C(i)C(j) 7 x=0 y=0 7 p(x, y) cos (2x + 1)iπ 16 cos (2y + 1)jπ. 16 Jednačinu (3.3) možemo ekvivalentno zapisati u matričnom obliku: D = T P T T gde elemente matrice T odred ujemo iz uslova: T i,j = 1 N, ako je i = 0 2 N cos (2j+1)iπ 2N, ako je i > 0. (3.6) Konkretno, za blok dimenzije 8 8 matrica T ima sledeći oblik: T = Na crno-beloj slici pikseli uzimaju celobrojne vrednosti od 0 do 255, gde 0 predstavlja crnu a 255 belu boju. Vrednosti izmed u predstavljaju neku nijansu sive boje. Slika može sadržati na stotine blokova dimenzije 8 8 i operacije koje se vrše na prvom bloku vrše se i na svim ostalim u redosledu koji je opisan 17
19 3.4 Diskretna kosinusna transformacija 3 JPEG FORMAT ranije. Na primer, neka pikseli iz prvog bloka (u gornjem levom uglu originalne slike) imaju sledeće vrednosti: Original = S obzirom da je DCT dizajniran da radi sa pikselima čije su vrednosti od -128 do 127 od svake originalne vrednosti se oduzima 128. Dobija se matrica: M = Sada možemo da primenimo DCT pomoću množenja matrica: D = T MT T (3.7) U prethodnoj jednačini matrica M se najpre množi sa leve strane matricom T koja predstavlja DCT. Na ovaj način smo transformisali vrste. Kolone se transformišu množenjem matrice M sa desne strane transponovanom DCT matricom T T pri čemu dobijamo: D =
20 3.5 Kvantizacija 3 JPEG FORMAT Ova matrica se sastoji od 64 DCT koeficijenta c ij. Koeficijent u gornjem levom uglu (c 00 ) je po apsolutnoj vrednosti dosta veći od ostalih koeficijenata i on se naziva DC koeficijent jer on odgovara frekvenciji jednaka 0. Ostali koeficijenti su AC koeficijenti i oni odgovaraju različitim vrednostima frekvencija. Nazivi AC i DC su motivisani odgovarajućim nazivima za jednosmernu i naizmeničnu struju. Udaljavajući se od c 00 u svim pravcima, DCT koeficijenti odgovaraju sve višim i višim frekvencijama. Ljudsko oko je osetljivije na niske frekvencije, pa će ova činjenica da se iskoristi u procesu kvantizacije prilikom odbacivanja koeficijenata koji odgovaraju višim frekvencijama. 3.5 Kvantizacija Kvantizacija se u matematici definiše kao proces mapiranja vrednosti iz nekog većeg (često kontinualnog) skupa u manji diskretni skup vrednosti. Tipičan primer kvantizacije je zaokruživanje decimalnih brojeva na celobrojne vrednosti. Jedna od dobrih osobina kompresije JPEG formata se ogleda u tome da izborom različitih kvantizacionih matrica u procesu kvantizacije kontrolišemo stepen kompresije i kvalitet slike. Ovo omogućava korisniku da izabere kvalitet na skali od 1 do 100, gde 1 predstavlja najveću kompresiju i najslabiji kvalitet slike, a 100 najmanju kompresiju ali daje najbolji kvalitet slike. Eksperimentima je utvrd eno da se najbolji rezultati dobijaju za vrednost kvaliteta 50, a odgovarajuća matrica ima sledeći oblik: Q 50 = Ova matrica se koristi za kvantizaciju luminanse, dok se za oba kanala hromi- 19
21 3.5 Kvantizacija 3 JPEG FORMAT nanse koristi sledeća matrica: Q 50 = Kvantizaciona matrica se potom skalira tako što se množi odgovarajućim koeficijentom skaliranja (Scaling Factor - SF). Ako sa QF (Quality Factor) označimo željeni kvalitet kompresije onda se SF dobija na sledeći način: SF = 1, ako je QF = QF, 50 ako je 50 QF > QF, ako je QF < 50. Svaki element matrice Q se potom skalira na sledeći način: Q i,j = Q i,j SF + 50, za svako i, j = 1,..., N. 100 Elementi transformisane matrice slike D se dele odgovarajućim elementima skalirane kvantizacione matrice Q. Dobijene vrednosti se potom zaokružuju na najbliži ceo broj: ( ) Di,j B i,j = round, za svako i, j = 1,..., N. Q i,j Za matricu D iz prethodnog primera dobijamo: B =
22 3.6 Kodiranje 3 JPEG FORMAT Ranije smo spomenuli da koeficijenti koji su bliži gornjem levom uglu matrice odgovaraju nižim frekvencijama na koje je ljudsko oko osetljivije. Takod e je zanimljiv efekat korišćenja različitih kvantizaconih matrica: za Q 10 matrica B će imati veliki broj nula, dok je za Q 90 broj nula veoma mali. 3.6 Kodiranje Proces kodiranja započinje tako što se koeficijenti matrice B posmatraju u cik-cak(zig-zag) redosledu (Slika (2.4)), a potom se primenjuje RLE (Run- Length Encoding) algoritam. Ovaj algoritam združuje bliske vrednosti koeficijenata, koeficijenti različiti od 0 se kodiraju pomoću Hafmanovog koda. Kao alternativa Hafmanovom kodiranju može da se koristi aritmetičko kodiranje. Kodiranje i dekodiranje aritmetičkim kodom je sporije u odnosu na Hafmanov kod, ali kodirane slike su obično 5-7% manje u pogledu memorije koja je potrebna za njihovo čuvanje. Slika 3.4: Cik-cak redosled obilaska matrice Na ovaj način smo blok dimenzije 8 8 preslikali u niz dimenzije DC koeficijent (c 00 ) se kodira drugačije u odnosu na AC koeficijente. Umesto stvarne vrednosti DC koeficijenta, kodira se razlika vrednosti trenutnog i prethodnog bloka (osim prvog bloka). Hafmanovo kodiranje zahteva jednu ili više Hafmanovih kodnih tabela, a iste tabele se koriste i kod kodiranja i kod dekodiranja. Hafmanove tabele su najčešće predefinisane i onda se samo iskoriste za kodi- 21
23 3.6 Kodiranje 3 JPEG FORMAT ranje, a u red im slučajevima se izračunavaju za konkretnu sliku u toku samog procesa kodiranja. Prilikom kodiranja svaki AC koeficijent različit od 0 se predstavlja pomoću 2 simbola: 1. Simbol 1: (RUNLENGTH, SIZE) 2. Simbol 2: (AMPLITUDE) gde su: RUNLENGTH - broj uzastopnih koeficijenata jednakih 0 koji su prethodili posmatranom koeficijentu; SIZE - broj potrebnih bitova za kodiranje; AMPLITUDE - vrednost koeficijenta izražena u bitovima. DC koeficijent se predstavlja u obliku (SIZE)(AMPLITUDE) jer u ovom slučaju uvek važi RUNLENGTH=0. Za negativne vrednosti amplitude se koriste komplementne vrednosti nad bitovima: s obzirom da je 10 binarna vrednost broja 2, onda je 01 binarna vrednost broja -2. Hafmanova tabela koja se najčešće koristi za kodiranje Simbola 1 DC koeficijenta data je na Slici (2.5) Slika 3.5: Hafmanova tabela za DC koeficijente Ako je potrebno kodirati vrednost 3 (označeno plavom bojom u Hafmanovoj tabeli), onda osnovu kodne reči iz odgovarajućeg reda tabele (u ovom slučaju je 22
24 3.6 Kodiranje 3 JPEG FORMAT to 100) dodajemo odgovarajuću binarnu vrednost (11). Dakle, dobijamo kodnu reč RUNLENGTH predstavlja broj nula od 0 do 15, ali kako broj uzastopnih nula može biti veći od 15 onda se u tom slučaju koristi specijalni simbol (15, 0) za vrednost RUNLENGTH=16. Ovakvih uzastopnih slučajeva može biti najviše tri, nakon čega se nalazi Simbol 2, osim u slučaju kada je poslednja nula ustvari poslednji AC koeficijent. Tada se koristi specijalan simbol (0,0) ili EOB (End- Of-Block) da označi kraj bloka. AC koeficijenti se kodiraju na osnovu tabele sa Slike (2.6) Slika 3.6: Hafmanova tabela za AC koeficijente Za odred ivanje kategorije kojoj AC koeficijent pripada može se iskoristiti tabela za DC koeficijente. Na primer, 24 se nalazi u kategoriji 5, pa (0,24) kodiramo sa , -4 je u kategoriji 3, pa (1,-4) kodiramo sa Primer 3.1. Neka nakon kvantizacije imamo sledeću matricu:
25 3.7 Dekompresija 3 JPEG FORMAT Ako je, recimo, u prethodnom bloku vrednost DC koeficijenta bila 12, onda je vrednost koju je potrebno kodirati = 3. Dobijamo reprezentaciju (2)(3) za SIZE=2 i AMPLITUDE=3. Sada je na sličan način potrebno predstaviti AC koeficijente. Prateći cik-cak redosled prvi koeficijent različit od 0 je -2 a njemu prethodi jedna 0, što nam daje reprezentaciju (1,2)(-2). Ovaj postupak ponovimo za sve AC koeficijente različite od 0. Na kraju imamo: (2)(3), (1, 2)( 2), (0, 1)( 1), (0, 1)( 1), (0, 1)( 1), (2, 1)( 1), (0, 0) Sada vršimo kodiranje Simbola 1 i dobijamo: (2) 100, (1, 2) 11011, (0, 1) 00, (2, 1) (0, 0), 1010 a potom i Simbola 2 na ranije opisan način: (3) 11, ( 2) 01, ( 1) 0. Dakle, 64 koeficijenta smo kodirali pomoću 31 bita: čime smo dobili efikasnu kompresiju jer je potrebno manje od 0.5 bita po koeficijentu umesto ranijih Dekompresija Rekonstrukcija slike počinje dekodiranjem kodnih reči čime dobijamo matricu C. Potom se svaki element ove matrice množi odgovarajućim elementom matrice sa početka procesa kvantizacije: B i,j = Q i,j C i,j. Na matricu B se primenjuje inverzna DCT i rezultat se zaokružuje na najbliži ceo broj. Konačno, svakom elementu se dodaje 128 i dobijamo matricu Approx koja predstavlja aproksimaciju originalnog bloka: Approx = round(t T B T ) Poslednji korak je transformacija iz YCbCr u RGB prostor boja: R Y G = (Cb 128). B (Cr 128) 24
26 3.7 Dekompresija 3 JPEG FORMAT Za naš primer, matrica Approx je sledećeg oblika: Approx = Razlika izmed u originalne i rekonstruisane matrice je: Original Approx = Ovo je veoma dobar rezultat ako se uzme u obzir da je skoro 70% DCT koeficijenata odbačeno u procesu kvantizacije. Slične rezultate dobićemo za sve blokove slike, pa će se dekompresovana slika malo razlikovati u odnosu na originalnu. 25
27 3.8 Eksperimentalni rezultati 3 JPEG FORMAT 3.8 Eksperimentalni rezultati Kao što smo ranije napomenuli, jedna od mera efikasnosti kompresije je kvalitet kompresije (QF). Kod slika sa kvalitetom kompresije 100 ima vrlo malo gubitaka, dok su gubici veliki kod slika kvaliteta kompresije 1. Za slike sa kvalitetom kompresije većim od 90 kažemo da su visokog kvaliteta, od su srednjeg, a od su slike slabog kvaliteta. Sve ispod 70 se obično smatra vrlo lošim kvalitetom. Ako postepeno smanjujemo kvalitet slike, prvi gubici na slici mogu da se uoče izmed u QF = 75 i QF = 50, zavisno od konkretne slike. Slika 3.7: a) Originalna slika; b) QF = 100; c) QF = 90; d) QF =
28 3.8 Eksperimentalni rezultati 3 JPEG FORMAT Slika 3.8: e) QF = 50; f) QF = 10; g) QF = 5; h) QF = 1. 27
29 4 JPEG2000 FORMAT 4 JPEG2000 format 4.1 Uvod JPEG2000 je standard za kompresiju slika razvijen godine od strane Med unarodne organizacije za standardizaciju (International Organization for Standardization - ISO) i Med unarodne komisije za elektrotehniku (International Electrotechnical Commission - IEC). Iako je JPEG do pojave JPEG2000 formata imao veoma široku primenu, postojala su ograničenja u mogućnostima koje su zahtevale interaktivne multimedijalne aplikacije, kao i njihovo korišćenje u komunikaciji. Značajan pomak u kompresiji slika ostvaren je primenom diskretne vejvlet transformacije (Discrete Wavelet Transform - DWT) i korišćenjem njihovih zanimljivih osobina razvijeni su mnogi algoritmi za kompresiju. JPEG2000 u svojoj osnovi koristi DWT da bi se prvenstveno prevazišli nedostaci JPEG formata. JPEG2000 standard je efikasan i koristi se u različitim sferama poput interneta, digitalne fotografije, arhiviranje slika, slike u medicini i astronomiji. Glavna mana JPEG2000 formata u pored enju sa JPEG formatom je dosta kompleksniji algoritam za kodiranje. Sa druge strane, glavna ideja pri definisanju JPEG2000 formata bila je da se slika kompresuje jednom, a da onda može da se dekompresuje na više različitih načina kako bi zadovoljila potrebe različitih aplikacija. Neke od glavnih prednosti JPEG2000 formata su: Odlične performanse kod kompresija sa manjim brojem bitova po pikselu: JPEG2000 nudi odlične performanse u pogledu vizuelnog kvaliteta slike i PSNR vrednosti kod kompresija sa manjim projem bitova po pikselu (ispod 0.25 bitova po pikselu) u odnosu na JPEG format. Samim tim, JPEG2000 ostvaruje veću kompresiju za ekvivalentni vizuelni kvalitet slike u odnosu na JPEG. Dobra kompresija nezavisno od broja bitova po pikselu: JPEG2000 format uspešno kompresuje kako binarne slike (1 bit po pikselu) tako i slike u boji sa po 16 ili 32 bita po pikselu. Slike velikih dimenzija sa velikim brojem komponenti: JPEG2000 standard dozvoljava maksimalne dimenzije slike (2 32 1) (2 32 1) i maksimalan broj komponenti Ova osobina omogućila je primenu JPEG2000 standarda u astronomiji. 28
30 4.2 Pretprocesiranje 4 JPEG2000 FORMAT Kompresija sa i bez gubitaka: Oba tipa kompresije su poželjna koristeći jednu arhitekturu kompresije. JPEG2000 to postiže korišćenjem reverzibilne celobrojne vejvlet transformacije. Veličina kompresovanog fajla može da se predefiniše: Proces kompresije može da traje sve dok se ne postigne željena veličina fajla i tad se kompresija prekida. Ova osobina je bitna kod aplikacija ili ured aja sa ograničenim baferom, kao što su skeneri i štampači. Progresivni prenos po pikselu i/ili rezoluciji: Ova osobina je poželjna kod sporijih kanala komunikacije i ogleda se u tome da se tačnost piksela i/ili rezolucija povećava sa svakim sledećim primljenim i dekompresovanim bitom. Kodiranje regiona interesovanja (Region of Interest - ROI): Ponekad je poželjno da odred eni delovi slike koji su veće važnosti od ostatka slike budu kodirani drugačije od ostatka slike. Na primer, kod slika u medicini jedan ili više regiona na slici mogu biti bitniji i oni se mogu kompresovati bez gubitaka zbog očuvanja tačnosti podataka, dok se ostali delovi slike kompresuju sa gubicima. JPEG2000 standard dozvoljava uvod enje stepena interesovanja čime se moše definisati kompresija na svakom regionu posebno. Takod e, pristupanjem odred enom bloku kompresovanih bitova moguće su operacije na odred enom regionu slike poput rotacije, translacije, skaliranja. Originalna slika može da sadrži jednu ili više komponenata. Iako najčešće, slike u boji sadrže 3 komponente (RGB ili YCbCr model boja), JPEG2000 format podržava do (2 14 ) komponenti. Glavni delovi JPEG2000 enkodera su pretprocesiranje, diskretna vejvlet transformacija, kvantizacija i kodiranje entropije kao što je prikazano na slici (4.1)). 4.2 Pretprocesiranje Faza pretprocesiranja sastoji se od tri opciona dela: podela na blokove ili popločavanje (tiling), DC pomeranje i transformacija multi-komponenti. 29
31 4.2 Pretprocesiranje 4 JPEG2000 FORMAT Slika 4.1: JPEG2000 blok diagram Podela na blokove U ovoj fazi ukoliko je slika velikih dimenzija onda može da se podeli na pravougaone blokove koji se ne preklapaju. Svi blokovi su istih dimenzija osim možda onih blokova koji su uz ivicu slike (u slučaju da dimenzija slike nije deljiva sa dimenzijom blokova). Dimenzije blokova mogu biti proizvoljne - blok može biti i samo jedan piksel a takod e i cela slika (kad imamo samo jedan blok). Svaki blok se kompresuje posebno koristeći svoje parametre kompresije i kao posledica toga moguće je pojavljivanje vidljivih artifakta blizu ivica bloka. Manji blokovi kreiraju veće artifakte na ivicama blokova a takod e i smanjuju efikasnost kompresije u pored enju sa većim blokovima. Očigledno da ukoliko nema podele slike na blokove vizuelni kvalitet je najbolji. Sa druge strane, ukoliko je dimenzija blokova (i same slike) velika, onda je potrebno više memorije za proces kodiranja, naročito zbog DWT izračunavanja. Zbog toga, podela na blokove je obično korisna kod aplikacija gde je količina memorije ograničena u pored enju sa dimenzijama slike DC pomeranje Najčešće se pikseli slike čuvaju kao neoznačene celobrojne vrednosti. Zbog matematičkih izračunavanja i pre bilo kakvih daljih transformacija potrebno je konvertovati i predstaviti vrednosti piksela pomoću reprezentacije potpunog 30
32 4.2 Pretprocesiranje 4 JPEG2000 FORMAT komplementa. DC pomeranje se primenjuje samo na neoznačene vrednosti i time se postiže da su te vrednosti centrirane oko nule. Kod slika čije su vrednosti piksela označeni celi brojevi kao što je to slučaj u kompjuterizovanoj tomografiji ne primenjuje se DC pomeranje jer su vrednosti već centrirane oko nule. DC pomeranjem se od svake vrednosti piksela oduzima 2 B 1, gde je B broj bitova kojim se predstavlja jedan piksel Transformacija multi-komponenti Transformacija multi-komponenti je efikasna prilikom smanjivanja korelacija (ako one postoje) izmed u multi-komponenti na slici koja sadrži te multikomponente. Rezultat tih transformacija je smanjivanje redundanse i povećavanje performansi kompresije. JPEG2000 standard predvid a transformacije multikomponenti samo za prve 3 komponente i zbog lakšeg razumevanja te komponente mogu da se interpretiraju kao komponente RGB modela. Generalno, svaka komponenta može biti drugačijih dimenzija i sa različitim brojem bitova po pikselu. Med utim, uslov transformacije multi-komponenti je da prve tri komponente budu istih dimenzija i sa istim brojem bitova po pikselu. JPEG2000 standard podržava reverzibilnu (RCT) i ireverzibilnu transformaciju boja (ICT). RCT se primenjuje na kompresiju i sa i bez gubitaka, dok se ICT primenjuje samo na kompresiju sa gubicima Reverzibilna transformacija boja Za kompresiju bez gubitaka primenjuje se samo RCT, jer slika može potpuno da bude rekonstruisana korišćenjem inverzne RTC. Takod e, RCT može da se koristi i kod kompresije sa gubicima i u tom slučaju greške koje se uvode pri kompresiji potiču od DWT i/ili kvantizacije, a ne od RCT. RCT se definiše na sledeći način: R + 2G + R Y = 4 dok je IRT definisana kao: U = B G V = R G 31
33 4.3 Kompresija 4 JPEG2000 FORMAT U + V G = Y 4 R = V + G B = U + G Ireverzibilna transformacija boja ICT kod JPEG2000 standarda odgovara transformaciji luminanse i hrominanse kod JPEG standarda. Y je komponenta luminanse i predstavlja intenzitet piksela (osvetljenje), dok su Cb i Cr komponente hrominanse koje daju informaciju o boji piksela. Jedina razlika u ovom koraku u odnosu na JPEG format je što kod JPEG2000 formata nije dozvoljeno da se komponente hrominanse sempluju. ICT je kao i kod JPEG formata definisan sa: Y Cb Cr = a inverzni ICT sa: R G = B 4.3 Kompresija Nakon opcione faze pretprocesiranja sledi faza kompresije pri čemu se svaka komponenta nezavisno kompresuje. Faza kompresije može da se podeli u tri glavna dela: diskretna vejvlet transformacija (DWT), kvantizacija i kodiranje. DWT razbija svaku komponentu na odred eni broj podgrupa sa različitim rezolucijama. Potom se svaka podgrupa nezavisno kvantizira pomoću parametara kvantizacije u slučaju kompresije sa gubicima. Kvantizirane podgrupe se potom dele na manje blokove jednakih dimenzija (osim blokova koji su na ivicama komponenti). Najčešće korišćene dimezije blokova su i Svaki blok se takod e kodira nezavisno. R G B Y Cb Cr 32
34 4.3 Kompresija 4 JPEG2000 FORMAT Vejvlet transformacija Jedna od glavnih osobina koja razlikuje JPEG2000 od JPEG formata je korišćenje diskretne vejvlet transformacije umesto diskretne kosinusne transformacije. Matematički, talas (wave) se definiše kao sinusiodna funkcija ili proces koje je periodičan u prostoru i vremenu. Nasuprot sinusoidnim funkcijama, vejvlet je mali talas čija je energija koncentrisana u vremenu. Sam pojam wavelet je prvi put upotrebljen u seizmologiji da označi smetnje koje nastaju usled naglih impulsa izazvanih zemljotresima. Osobine vejvleta dozvoljavaju istovremenu analizu signala vremena i frekvencije zbog činjenice da je njihova energija koncentrisana u vremenu i kao takvi oni poseduju periodične osobine talasa. Sa L 2 označavamo prostor kvadratnih integrabilnih funkcija i sa R skup realnih brojeva. Vejvlet je svaka funkcija ψ L 2 (R)\{0} za koju važi: + ψ(ω) 2 c ψ = 2π dω < (4.8) ω Da bi prethodni uslov bio zadovoljen dovoljno je da ψ ima srednju vrednost jednaku nuli, odnosno da važi: ψ(0) = + ψ(t) dt = 0 (4.9) Ovo svojstvo govori o oscilatornoj prirodi funkcije ψ. Na osnovu definicije 4.8 funkcija ψ može biti vejvlet ukoliko brzo opada kao nuli kad t. Pomenuta svojstva odgovaraju pojmu vejvlet ( mali talas ) jer ukazuju na činjenicu da funkcija osciluje oko vremenske ose na veoma malom intervalu, a da izvan tog intervala brzo opada ka nuli. Pošto oblik vejvleta nije jedinstven postavlja se pitanje kako konstruisati vejvlet. Svojstvo koje je poželjno postići prilikom konstrukcije vejvleta je da on ima što više momenata jednakih nuli. Funkcija ψ ima M momenata jednakih nuli ako važi: + ψ(t)t m dt = 0, m = 0,..., M 1 (4.10) Signal se sastoji iz delova koji su glatki i delova na kojima se dešavaju odred ene promene ili prekidi. Ako signal može da se predstavi po delovima glatkim funkcijama, tada će vejvlet transformacija na glatkim delovima imati vrednost nula ukoliko ψ ima dovoljno nula momenata. To omogućava da se detektuju i 33
35 4.3 Kompresija 4 JPEG2000 FORMAT lokalizuju promene. Pomoću M puta diferencijabilne funkcije φ(t) kontruišemo vejvlet ψ(t) na sledeći način: ψ(t) = dm φ dt M (4.11) Postoje vejvleti koji su ustaljeni u praksi i neki od najkorišćenijih su: Harov vejvlet (za M = 1) - jedan od najprostijih vejvleta i definisan je na sledeći način: 1, 0 t < ψ(t) = 1, 2 t < 1 0, inače Skup diskretno transliranih i skaliranih Harovih funkcija čini najprostiju ortonormalnu bazu. Med utim, ovaj vejvlet je slabo lokalizovan u frekventnom domenu kao posledica prekidnosti funkcije u vremenskom domenu i to mu je glavni nedostatak koji ga limitira za odred ene aplikacije. Predstavljanjem signala u vremenskom domenu dobijamo informaciju kako se amplituda tog signala menja za neki vremenski period. Sa druge strane, predstavljanje signala u frekventnom domenu daje informaciju o tome koliko se puta odred ena vrednost signala ponovila za neki vremenski period. Slika 4.2: Harov vejvlet 34
36 4.3 Kompresija 4 JPEG2000 FORMAT Sinusni vejvlet - ovaj vejvlet je takod e jedan od najjednostavnijih i u pitanju je jedan ciklus sinusne funkcije: { 1 ψ(t) = π sin(t), t π 0, inače Slika 4.3: Sinusni vejvlet Meksički šešir vejvlet - se definiše na sledeći način: ψ(t) = 2 3 π 1 4 (1 t 2 )e t2 2 Sam oblik vejvleta podseća na meksički šešir, pa odatle potiče i naziv. Ovaj vejvlet se često koristi u aplikacijama za detekciju ivica. Šenonov vejvlet - je vrlo popularan u teoriji. Ima lošiju vremensku rezoluciju, ali mu je frekventna rezolucija vrlo dobra. Definisan je na sledeći način: ψ(t) = sin 2πt sin πt πt Vejvleti su funkcije dobijene od jedne (bazne) funkcije proširivanjem (skaliranjem) i pomeranjem (translacijom) u vremenskom (frekventnom) domenu. Bazna funkcija se naziva prototip ili majka vejvlet funkcija. Ako prototip funkciju označimo sa Ψ(t), onda odgovarajuće vejvlete možemo definisati kao: ψ a,b (t) = 1 a ψ 35 ( ) t b a (4.12)
37 4.3 Kompresija 4 JPEG2000 FORMAT Slika 4.4: Meksički šešir vejvlet Slika 4.5: Šenonov vejvlet gde su a i b proizvoljni realni brojevi. Promenljive a i b predstavljaju parametre skaliranja i translacije na vremenskoj osi, redom. Iz jednačine (4.12) očigledno važi: Za proizvoljno a 1 i b = 0, dobija se: ψ(t) = ψ 1,0 (t) (4.13) ψ a,0 (t) = 1 a ψ ( ) t a (4.14) U jednačini (4.14) funkcija ψ a,0 (t) je skalirana po vremenu (za vrednost a) i skalirana po amplitudi (za vrednost a ) verzija prototipa funkcije ψ(t) definisane u jednačini (4.13). Parametar a izaziva skupljanje funkcije ψ a,b (t) po vremenskoj osi kad je a < 1 i širenje funkcije kad je a > 1. Zbog toga se parametar a naziva parametrom proširenja ili skaliranja. Funkcija ψ a,b (t) 36
38 4.3 Kompresija 4 JPEG2000 FORMAT predstavlja pomeraj funkcije ψ a,0 (t) udesno duž vremenske ose za vrednost b kad je b > 0 i pomeraj ulevo kad je b < 0. Zbog ove osobine parametar b predstavlja parametar pomeranja ili translacije. Na slici (4.6) je prikazan prototip vejvlet i odgovarajuće skaliranje duž vremenske ose za parametar a = α. Slika 4.6: a) Prototip vejvlet ψ(t) b) ψ(t/α), 0 < α < 1; c) ψ(t/α), α >1 Na osnovu ove definicije vejvleta, vejvlet transformacija (WT) funkcije (signala) f(t) se matematički definiše kao: W (a, b) = + ψ a,b (t)f(t) dt (4.15) Kod inverzne transformacije dobija se vrednost f(t) na osnovu W (a, b) je: f(t) = 1 C + a= + b= 1 a 2 W (a, b)ψ a,b(t) da db (4.16) 37
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић
 Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Драган Пејић, Бојан Вујичић, Небојша Пјевалица,
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Драган Пејић, Бојан Вујичић, Небојша Пјевалица,
1
 Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Техничко решење: Софтвер за симулацију стохастичког ортогоналног мерила сигнала, његовог интеграла и диференцијала Руководилац пројекта: Владимир Вуји
 Техничко решење: Софтвер за симулацију стохастичког ортогоналног мерила сигнала, његовог интеграла и диференцијала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Велибор
Техничко решење: Софтвер за симулацију стохастичког ортогоналног мерила сигнала, његовог интеграла и диференцијала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Велибор
RG_V_05_Transformacije 3D
 Računarska grafika - vežbe 5 Transformacije u 3D grafici Transformacije u 3D grafici Slično kao i u D grafici, uz razlike: matrice su 4x4 postoji posebna matrica projekcije Konvencije: desni pravougli
Računarska grafika - vežbe 5 Transformacije u 3D grafici Transformacije u 3D grafici Slično kao i u D grafici, uz razlike: matrice su 4x4 postoji posebna matrica projekcije Konvencije: desni pravougli
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA Seminarski rad u okviru predmeta Računalna forenzika BETTER PORTABLE GRAPHICS FORMAT Matej
 SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA Seminarski rad u okviru predmeta Računalna forenzika BETTER PORTABLE GRAPHICS FORMAT Matej Crnac Zagreb, siječanj 2018 Sadržaj Uvod 2 BPG format
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA Seminarski rad u okviru predmeta Računalna forenzika BETTER PORTABLE GRAPHICS FORMAT Matej Crnac Zagreb, siječanj 2018 Sadržaj Uvod 2 BPG format
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аут
 Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Иван Жупунски, Небојша Пјевалица, Марјан Урекар,
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Иван Жупунски, Небојша Пјевалица, Марјан Урекар,
Орт колоквијум
 II колоквијум из Основа рачунарске технике I - 27/28 (.6.28.) Р е ш е њ е Задатак На улазе x, x 2, x 3, x 4 комбинационе мреже, са излазом z, долази четворобитни BCD број. Ако број са улаза при дељењу
II колоквијум из Основа рачунарске технике I - 27/28 (.6.28.) Р е ш е њ е Задатак На улазе x, x 2, x 3, x 4 комбинационе мреже, са излазом z, долази четворобитни BCD број. Ако број са улаза при дељењу
Mere slicnosti
 Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
LAB PRAKTIKUM OR1 _ETR_
 UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA, TELEKOMUNIKACIJE I RAČUNARI PREDMET: OSNOVE RAČUNARSTVA 1 FOND ČASOVA: 2+1+1 LABORATORIJSKA VJEŽBA BROJ 1 NAZIV: REALIZACIJA
UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA, TELEKOMUNIKACIJE I RAČUNARI PREDMET: OSNOVE RAČUNARSTVA 1 FOND ČASOVA: 2+1+1 LABORATORIJSKA VJEŽBA BROJ 1 NAZIV: REALIZACIJA
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica
 Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
Inženjering informacionih sistema
 Fakultet tehničkih nauka, Novi Sad Inženjering informacionih sistema Dr Ivan Luković Dr Slavica Kordić Nikola Obrenović Milanka Bjelica Dr Jelena Borocki Dr Milan Delić UML UML (Unified Modeling Language)
Fakultet tehničkih nauka, Novi Sad Inženjering informacionih sistema Dr Ivan Luković Dr Slavica Kordić Nikola Obrenović Milanka Bjelica Dr Jelena Borocki Dr Milan Delić UML UML (Unified Modeling Language)
Орт колоквијум
 Испит из Основа рачунарске технике - / (6.6.. Р е ш е њ е Задатак Комбинациона мрежа има пет улаза, по два за број освојених сетова тенисера и један сигнал који одлучује ко је бољи уколико је резултат
Испит из Основа рачунарске технике - / (6.6.. Р е ш е њ е Задатак Комбинациона мрежа има пет улаза, по два за број освојених сетова тенисера и један сигнал који одлучује ко је бољи уколико је резултат
1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan
 1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan jednačinom oblika: a 11 x 2 + 2a 12 xy + a 22 y 2
1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan jednačinom oblika: a 11 x 2 + 2a 12 xy + a 22 y 2
P1.1 Analiza efikasnosti algoritama 1
 Analiza efikasnosti algoritama I Asimptotske notacije Master metoda (teorema) 1 Asimptotske notacije (1/2) Služe za opis vremena izvršenja algoritma T(n) gde je n N veličina ulaznih podataka npr. br. elemenata
Analiza efikasnosti algoritama I Asimptotske notacije Master metoda (teorema) 1 Asimptotske notacije (1/2) Služe za opis vremena izvršenja algoritma T(n) gde je n N veličina ulaznih podataka npr. br. elemenata
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K.
 1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K. Elementi a k K su koeficijenti polinoma P (x). Ako
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K. Elementi a k K su koeficijenti polinoma P (x). Ako
Algoritmi i arhitekture DSP I
 Univerzitet u Novom Sadu Fakultet Tehničkih Nauka Katedra za računarsku tehniku i međuračunarske komunikacije Algoritmi i arhitekture DSP I INTERNA ORGANIACIJA DIGITALNOG PROCESORA A OBRADU SIGNALA INTERNA
Univerzitet u Novom Sadu Fakultet Tehničkih Nauka Katedra za računarsku tehniku i međuračunarske komunikacije Algoritmi i arhitekture DSP I INTERNA ORGANIACIJA DIGITALNOG PROCESORA A OBRADU SIGNALA INTERNA
Microsoft PowerPoint - Predavanje3.ppt
 Фрактална геометрија и фрактали у архитектури функционални системи Улаз Низ правила (функција F) Излаз Фрактална геометрија и фрактали у архитектури функционални системи Функционални систем: Улаз Низ правила
Фрактална геометрија и фрактали у архитектури функционални системи Улаз Низ правила (функција F) Излаз Фрактална геометрија и фрактали у архитектури функционални системи Функционални систем: Улаз Низ правила
TEORIJA SIGNALA I INFORMACIJA
 Multiple Input/Multiple Output sistemi MIMO sistemi Ulazi (pobude) Izlazi (odzivi) u 1 u 2 y 1 y 2 u k y r Obrada=Matematički model Načini realizacije: fizički sistemi (hardware) i algoritmi (software)
Multiple Input/Multiple Output sistemi MIMO sistemi Ulazi (pobude) Izlazi (odzivi) u 1 u 2 y 1 y 2 u k y r Obrada=Matematički model Načini realizacije: fizički sistemi (hardware) i algoritmi (software)
ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 2006/2007 године I разред
 ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 006/007 године разред. Електрични систем се састоји из отпорника повезаних тако
ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 006/007 године разред. Електрични систем се састоји из отпорника повезаних тако
Microsoft Word - 15ms261
 Zadatak 6 (Mirko, elektrotehnička škola) Rješenje 6 Odredite sup S, inf S, ma S i min S u skupu R ako je S = { R } a b = a a b + b a b, c < 0 a c b c. ( ), : 5. Skratiti razlomak znači brojnik i nazivnik
Zadatak 6 (Mirko, elektrotehnička škola) Rješenje 6 Odredite sup S, inf S, ma S i min S u skupu R ako je S = { R } a b = a a b + b a b, c < 0 a c b c. ( ), : 5. Skratiti razlomak znači brojnik i nazivnik
Analiticka geometrija
 Analitička geometrija Predavanje 3 Konusni preseci (krive drugog reda, kvadratne krive) Novi Sad, 2018. Milica Žigić (PMF, UNS 2018) Analitička geometrija predavanje 3 1 / 22 Ime s obzirom na karakteristike
Analitička geometrija Predavanje 3 Konusni preseci (krive drugog reda, kvadratne krive) Novi Sad, 2018. Milica Žigić (PMF, UNS 2018) Analitička geometrija predavanje 3 1 / 22 Ime s obzirom na karakteristike
Matematka 1 Zadaci za vežbe Oktobar Uvod 1.1. Izračunati vrednost izraza (bez upotrebe pomoćnih sredstava): ( ) [ a) : b) 3 3
 Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
ТРОУГАО БРЗИНА и математичка неисправност Лоренцове трансформације у специјалној теорији релативности Александар Вукеља www.
 ТРОУГАО БРЗИНА и математичка неисправност Лоренцове трансформације у специјалној теорији релативности Александар Вукеља aleksandar@masstheory.org www.masstheory.org Август 2007 О ауторским правима: Дело
ТРОУГАО БРЗИНА и математичка неисправност Лоренцове трансформације у специјалној теорији релативности Александар Вукеља aleksandar@masstheory.org www.masstheory.org Август 2007 О ауторским правима: Дело
P11.3 Analiza zivotnog veka, Graf smetnji
 Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
Математика основни ниво 1. Одреди елементе скупова A, B, C: a) б) A = B = C = 2. Запиши елементе скупова A, B, C на основу слике: A = B = C = 3. Броје
 1. Одреди елементе скупова A, B, C: a) б) A = B = C = 2. Запиши елементе скупова A, B, C на основу слике: A = B = C = 3. Бројеве записане римским цифрама запиши арапским: VIII LI XXVI CDXLIX MDCLXVI XXXIX
1. Одреди елементе скупова A, B, C: a) б) A = B = C = 2. Запиши елементе скупова A, B, C на основу слике: A = B = C = 3. Бројеве записане римским цифрама запиши арапским: VIII LI XXVI CDXLIX MDCLXVI XXXIX
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe
 6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe, očekuje se da su koordinate celobrojne. U slučaju
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe, očekuje se da su koordinate celobrojne. U slučaju
Prikaz slike na monitoru i pisaču
 CRT monitori s katodnom cijevi i LCD monitori na bazi tekućih kristala koji su gotovo istisnuli iz upotrebe prethodno navedene. LED monitori- Light Emitting Diode, zasniva se na elektrodama i diodama koje
CRT monitori s katodnom cijevi i LCD monitori na bazi tekućih kristala koji su gotovo istisnuli iz upotrebe prethodno navedene. LED monitori- Light Emitting Diode, zasniva se na elektrodama i diodama koje
STABILNOST SISTEMA
 STABILNOST SISTEMA Najvaznija osobina sistema automatskog upravljanja je stabilnost. Generalni zahtev koji se postavlja pred projektanta jeste da projektovani i realizovani sistem automatskog upravljanja
STABILNOST SISTEMA Najvaznija osobina sistema automatskog upravljanja je stabilnost. Generalni zahtev koji se postavlja pred projektanta jeste da projektovani i realizovani sistem automatskog upravljanja
PowerPoint Presentation
 УВОД Дa би рaчунaри нa мрежи могли међусобно да кoмуницирaју и рaзмeњују пoдaткe, пoтрeбнo je: дa сe увeду ПРOТOКOЛИ (утврђeна прaвилa и процедуре за комуникацију) да постоје АДРEСE кoje су jeдинствeнe
УВОД Дa би рaчунaри нa мрежи могли међусобно да кoмуницирaју и рaзмeњују пoдaткe, пoтрeбнo je: дa сe увeду ПРOТOКOЛИ (утврђeна прaвилa и процедуре за комуникацију) да постоје АДРEСE кoje су jeдинствeнe
PowerPoint Presentation
 Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Увод у организацију и архитектуру рачунара 1
 Увод у организацију и архитектуру рачунара 2 Александар Картељ kartelj@matf.bg.ac.rs Напомена: садржај ових слајдова је преузет од проф. Саше Малкова Увод у организацију и архитектуру рачунара 2 1 Секвенцијалне
Увод у организацију и архитектуру рачунара 2 Александар Картељ kartelj@matf.bg.ac.rs Напомена: садржај ових слајдова је преузет од проф. Саше Малкова Увод у организацију и архитектуру рачунара 2 1 Секвенцијалне
Veeeeeliki brojevi
 Matematička gimnazija Nedelja informatike 3 12. decembar 2016. Uvod Postoji 10 tipova ljudi na svetu, oni koji razumeju binarni sistem, oni koji ne razumeju binarni sistem i oni koji nisu očekivali šalu
Matematička gimnazija Nedelja informatike 3 12. decembar 2016. Uvod Postoji 10 tipova ljudi na svetu, oni koji razumeju binarni sistem, oni koji ne razumeju binarni sistem i oni koji nisu očekivali šalu
Matrice. Algebarske operacije s matricama. - Predavanje I
 Matrice.. Predavanje I Ines Radošević inesr@math.uniri.hr Odjel za matematiku Sveučilišta u Rijeci Matrice... Matrice... Podsjeti se... skup, element skupa,..., matematička logika skupovi brojeva N,...,
Matrice.. Predavanje I Ines Radošević inesr@math.uniri.hr Odjel za matematiku Sveučilišta u Rijeci Matrice... Matrice... Podsjeti se... skup, element skupa,..., matematička logika skupovi brojeva N,...,
Verovatnoća - kolokvijum 17. decembar Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je
 Verovatnoća - kolokvijum 17. decembar 2016. 1. Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je 0.8. Ako je ispit težak, verovatnoća da se prvo pitanje
Verovatnoća - kolokvijum 17. decembar 2016. 1. Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je 0.8. Ako je ispit težak, verovatnoća da se prvo pitanje
Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odr
 Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odrediti njene krajeve. b) Odrediti sledeće skupove: -
Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odrediti njene krajeve. b) Odrediti sledeće skupove: -
Microsoft Word - Ispitivanje toka i grafik funkcije V deo
 . Ispitati tok i skicirati grafik funkcije y= arcsin + Oblast definisanosti (domen) Podsetimo se grafika elementarnih funkcija i kako izgleda arcsin funkcija: y - y=arcsin Funkcija je definisana za [,]
. Ispitati tok i skicirati grafik funkcije y= arcsin + Oblast definisanosti (domen) Podsetimo se grafika elementarnih funkcija i kako izgleda arcsin funkcija: y - y=arcsin Funkcija je definisana za [,]
Microsoft Word - 6ms001
 Zadatak 001 (Anela, ekonomska škola) Riješi sustav jednadžbi: 5 z = 0 + + z = 14 4 + + z = 16 Rješenje 001 Sustav rješavamo Gaussovom metodom eliminacije (isključivanja). Gaussova metoda provodi se pomoću
Zadatak 001 (Anela, ekonomska škola) Riješi sustav jednadžbi: 5 z = 0 + + z = 14 4 + + z = 16 Rješenje 001 Sustav rješavamo Gaussovom metodom eliminacije (isključivanja). Gaussova metoda provodi se pomoću
PRIRODNO MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA RAČUNARSKE NAUKE Utorak, godine PRIJEMNI ISPIT IZ INFORMATIKE 1. Koja od navedenih ekste
 PRIRODNO MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA RAČUNARSKE NAUKE Utorak, 5.06.019. godine PRIJEMNI ISPIT IZ INFORMATIKE 1. Koja od navedenih ekstenzija se najčešće koristi za tekstualne datoteke? a)
PRIRODNO MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA RAČUNARSKE NAUKE Utorak, 5.06.019. godine PRIJEMNI ISPIT IZ INFORMATIKE 1. Koja od navedenih ekstenzija se najčešće koristi za tekstualne datoteke? a)
PowerPoint Presentation
 Nedjelja 6 - Lekcija Projiciranje Postupci projiciranja Projiciranje je postupak prikazivanja oblika nekog, u opštem slučaju trodimenzionalnog, predmeta dvodimenzionalnim crtežom. Postupci projiciranja
Nedjelja 6 - Lekcija Projiciranje Postupci projiciranja Projiciranje je postupak prikazivanja oblika nekog, u opštem slučaju trodimenzionalnog, predmeta dvodimenzionalnim crtežom. Postupci projiciranja
Tеорија одлучивања
 Tеорија одлучивања Аналитички хијерархијски процес Циљ предавања Упознавање са АХП медотом Врсте АХП методе Предности и недостаци АХП методе Софтвери АХП Expert Choice MakeItRational (.com) Пример АХП
Tеорија одлучивања Аналитички хијерархијски процес Циљ предавања Упознавање са АХП медотом Врсте АХП методе Предности и недостаци АХП методе Софтвери АХП Expert Choice MakeItRational (.com) Пример АХП
Microsoft PowerPoint - vezbe 4. Merenja u telekomunikacionim mrežama
 Merenja u telekomunikacionim mrežama Merenja telefonskog saobraćaja Primer 1 - TCBH Na osnovu najviših vrednosti intenziteta saobraćaja datih za 20 mernih dana (tabela), pomoću metode TCBH, pronaći čas
Merenja u telekomunikacionim mrežama Merenja telefonskog saobraćaja Primer 1 - TCBH Na osnovu najviših vrednosti intenziteta saobraćaja datih za 20 mernih dana (tabela), pomoću metode TCBH, pronaći čas
СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за векто
![СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за векто СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за векто](/thumbs/102/155791469.jpg) СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за вектор a (коjи може бити и дужине нула) и неке изометриjе
СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за вектор a (коjи може бити и дужине нула) и неке изометриjе
Skripte2013
 Chapter 2 Algebarske strukture Preslikivanje f : A n! A se naziva n-arna operacija na skupu A Ako je n =2, kažemo da je f : A A! A binarna operacija na A Kažemo da je operacija f arnosti n, u oznaci ar
Chapter 2 Algebarske strukture Preslikivanje f : A n! A se naziva n-arna operacija na skupu A Ako je n =2, kažemo da je f : A A! A binarna operacija na A Kažemo da je operacija f arnosti n, u oznaci ar
Ravno kretanje krutog tela
 Ravno kretanje krutog tela Brzine tačaka tela u reprezentativnom preseku Ubrzanja tačaka u reprezentativnom preseku Primer određivanja brzina i ubrzanja kod ravnog mehanizma Ravno kretanje krutog tela
Ravno kretanje krutog tela Brzine tačaka tela u reprezentativnom preseku Ubrzanja tačaka u reprezentativnom preseku Primer određivanja brzina i ubrzanja kod ravnog mehanizma Ravno kretanje krutog tela
08 RSA1
 Преглед ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције RSA алгоритам Биће објашњено: RSA алгоритам алгоритам прорачунски аспекти ефикасност коришћењем јавног кључа генерисање кључа сигурност проблем
Преглед ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције RSA алгоритам Биће објашњено: RSA алгоритам алгоритам прорачунски аспекти ефикасност коришћењем јавног кључа генерисање кључа сигурност проблем
Microsoft Word - CAD sistemi
 U opštem slučaju, se mogu podeliti na 2D i 3D. 2D Prvo pojavljivanje 2D CAD sistema se dogodilo pre više od 30 godina. Do tada su inženjeri koristili table za crtanje (kulman), a zajednički jezik komuniciranja
U opštem slučaju, se mogu podeliti na 2D i 3D. 2D Prvo pojavljivanje 2D CAD sistema se dogodilo pre više od 30 godina. Do tada su inženjeri koristili table za crtanje (kulman), a zajednički jezik komuniciranja
Microsoft Word - ASIMPTOTE FUNKCIJA.doc
 ASIMPTOTE FUNKCIJA Naš savet je da najpre dobro proučite granične vrednosti funkcija Neki profesori vole da asimptote funkcija ispituju kao ponašanje funkcije na krajevima oblasti definisanosti, pa kako
ASIMPTOTE FUNKCIJA Naš savet je da najpre dobro proučite granične vrednosti funkcija Neki profesori vole da asimptote funkcija ispituju kao ponašanje funkcije na krajevima oblasti definisanosti, pa kako
Postojanost boja
 Korištenje distribucije osvjetljenja za ostvaranje brzih i točnih metode za postojanost boja Nikola Banić 26. rujna 2014. Sadržaj Postojanost boja Ubrzavanje lokalnog podešavanja boja Distribucija najčešćih
Korištenje distribucije osvjetljenja za ostvaranje brzih i točnih metode za postojanost boja Nikola Banić 26. rujna 2014. Sadržaj Postojanost boja Ubrzavanje lokalnog podešavanja boja Distribucija najčešćih
Uvod u statistiku
 Uvod u statistiku Osnovni pojmovi Statistika nauka o podacima Uključuje prikupljanje, klasifikaciju, prikaz, obradu i interpretaciju podataka Staistička jedinica objekat kome se mjeri neko svojstvo. Svi
Uvod u statistiku Osnovni pojmovi Statistika nauka o podacima Uključuje prikupljanje, klasifikaciju, prikaz, obradu i interpretaciju podataka Staistička jedinica objekat kome se mjeri neko svojstvo. Svi
Microsoft Word - predavanje8
 DERIVACIJA KOMPOZICIJE FUNKCIJA Ponekad je potrebno derivirati funkcije koje nisu jednostavne (složene su). Na primjer, funkcija sin2 je kompozicija funkcija sin (vanjska funkcija) i 2 (unutarnja funkcija).
DERIVACIJA KOMPOZICIJE FUNKCIJA Ponekad je potrebno derivirati funkcije koje nisu jednostavne (složene su). Na primjer, funkcija sin2 je kompozicija funkcija sin (vanjska funkcija) i 2 (unutarnja funkcija).
My_P_Red_Bin_Zbir_Free
 БИНОМНА ФОРМУЛА Шт треба знати пре почетка решавања задатака? I Треба знати биному формулу која даје одговор на питање чему је једнак развој једног бинома када га степенујемо са бројем 0 ( ) или ( ) 0!,
БИНОМНА ФОРМУЛА Шт треба знати пре почетка решавања задатака? I Треба знати биному формулу која даје одговор на питање чему је једнак развој једног бинома када га степенујемо са бројем 0 ( ) или ( ) 0!,
7. predavanje Vladimir Dananić 14. studenoga Vladimir Dananić () 7. predavanje 14. studenoga / 16
 7. predavanje Vladimir Dananić 14. studenoga 2011. Vladimir Dananić () 7. predavanje 14. studenoga 2011. 1 / 16 Sadržaj 1 Operator kutne količine gibanja 2 3 Zadatci Vladimir Dananić () 7. predavanje 14.
7. predavanje Vladimir Dananić 14. studenoga 2011. Vladimir Dananić () 7. predavanje 14. studenoga 2011. 1 / 16 Sadržaj 1 Operator kutne količine gibanja 2 3 Zadatci Vladimir Dananić () 7. predavanje 14.
Slide 1
 Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
Tutoring System for Distance Learning of Java Programming Language
 Deklaracija promenljivih Inicijalizacija promenljivih Deklaracija promenljive obuhvata: dodelu simboličkog imena promenljivoj i određivanje tipa promenljive (tip određuje koja će vrsta memorijskog registra
Deklaracija promenljivih Inicijalizacija promenljivih Deklaracija promenljive obuhvata: dodelu simboličkog imena promenljivoj i određivanje tipa promenljive (tip određuje koja će vrsta memorijskog registra
I колоквијум из Основа рачунарске технике I СИ- 2017/2018 ( ) Р е ш е њ е Задатак 1 Тачка А Потребно је прво пронаћи вредности функција f(x
 I колоквијум из Основа рачунарске технике I СИ- / (...) Р е ш е њ е Задатак Тачка А Потребно је прво пронаћи вредности функција f(x, x, x ) и g(x, x, x ) на свим векторима. f(x, x, x ) = x x + x x + x
I колоквијум из Основа рачунарске технике I СИ- / (...) Р е ш е њ е Задатак Тачка А Потребно је прво пронаћи вредности функција f(x, x, x ) и g(x, x, x ) на свим векторима. f(x, x, x ) = x x + x x + x
Prikaz znakova u računalu
 PRIKAZ ZNAKOVA U RAČUNALU Načini kodiranja ASCII 1 znak 7 bitova Prošireni ASCII 1 znak 8 bitova (1B) UNICODE 1 znak 16 bitova (2B) ZADATCI S MATURE ljetni rok, 2014., zadatak 11 Koliko se različitih znakova
PRIKAZ ZNAKOVA U RAČUNALU Načini kodiranja ASCII 1 znak 7 bitova Prošireni ASCII 1 znak 8 bitova (1B) UNICODE 1 znak 16 bitova (2B) ZADATCI S MATURE ljetni rok, 2014., zadatak 11 Koliko se različitih znakova
Microsoft Word - 11 Pokazivaci
 Pokazivači U dosadašnjem radu smo imali prilike da koristimo promenljive koje smo deklarisali na početku nekog bloka. Prilikom deklaracije promenljiva dobija jedinstveni naziv i odgovarajući prostor u
Pokazivači U dosadašnjem radu smo imali prilike da koristimo promenljive koje smo deklarisali na početku nekog bloka. Prilikom deklaracije promenljiva dobija jedinstveni naziv i odgovarajući prostor u
QFD METODA – PRIMER
 QFD METODA - PRIMER PROBLEM: U kompaniji X koja se bavi izradom kompjuterskih softvera uočen je pad prodaje konkretnog softvera - Softver za vođenje knjigovodstva. Kompanija X je raspolagala sa jednom
QFD METODA - PRIMER PROBLEM: U kompaniji X koja se bavi izradom kompjuterskih softvera uočen je pad prodaje konkretnog softvera - Softver za vođenje knjigovodstva. Kompanija X je raspolagala sa jednom
My_ST_FTNIspiti_Free
 ИСПИТНИ ЗАДАЦИ СУ ГРУПИСАНИ ПО ТЕМАМА: ЛИМЕСИ ИЗВОДИ ФУНКЦИЈЕ ЈЕДНЕ ПРОМЕНЉИВЕ ИСПИТИВАЊЕ ТОКА ФУНКЦИЈЕ ЕКСТРЕМИ ФУНКЦИЈЕ СА ВИШЕ ПРОМЕНЉИВИХ 5 ИНТЕГРАЛИ ДОДАТАК ФТН Испити С т р а н а Лимеси Одредити
ИСПИТНИ ЗАДАЦИ СУ ГРУПИСАНИ ПО ТЕМАМА: ЛИМЕСИ ИЗВОДИ ФУНКЦИЈЕ ЈЕДНЕ ПРОМЕНЉИВЕ ИСПИТИВАЊЕ ТОКА ФУНКЦИЈЕ ЕКСТРЕМИ ФУНКЦИЈЕ СА ВИШЕ ПРОМЕНЉИВИХ 5 ИНТЕГРАЛИ ДОДАТАК ФТН Испити С т р а н а Лимеси Одредити
PowerPoint Presentation
 Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Sa stanovišta pristupa problemu korišćenja kapaciteta, razlikuju se metode
Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Sa stanovišta pristupa problemu korišćenja kapaciteta, razlikuju se metode
SKRIPTE EKOF 2019/20 skripteekof.com Lekcija 1: Brojevni izrazi Lekcija 1: Brojevni izrazi Pregled lekcije U okviru ove lekcije imaćete priliku da nau
 Lekcija : Brojevni izrazi Pregled lekcije U okviru ove lekcije imaćete priliku da naučite sledeće: osnovni pojmovi o razlomcima proširivanje, skraćivanje, upoređivanje; zapis razlomka u okviru mešovitog
Lekcija : Brojevni izrazi Pregled lekcije U okviru ove lekcije imaćete priliku da naučite sledeće: osnovni pojmovi o razlomcima proširivanje, skraćivanje, upoređivanje; zapis razlomka u okviru mešovitog
06 Poverljivost simetricnih algoritama1
 ЗАШТИТА ПОДАТАКА Симетрични алгоритми заштите поверљивост симетричних алгоритама Преглед биће објашњено: коришћење симетричних алгоритама заштите како би се заштитила поверљивост потреба за добрим системом
ЗАШТИТА ПОДАТАКА Симетрични алгоритми заштите поверљивост симетричних алгоритама Преглед биће објашњено: коришћење симетричних алгоритама заштите како би се заштитила поверљивост потреба за добрим системом
ЕНЕРГЕТСКИ ПРЕТВАРАЧИ септембар 2005
 ЕНЕРГЕТСКИ ПРЕТВАРАЧИ јануар 00. год.. Пећ сачињена од три грејача отпорности =0Ω, везана у звезду, напаја се са мреже 3x380V, 50Hz, преко три фазна регулатора, као на слици. Угао паљења тиристора је α=90,
ЕНЕРГЕТСКИ ПРЕТВАРАЧИ јануар 00. год.. Пећ сачињена од три грејача отпорности =0Ω, везана у звезду, напаја се са мреже 3x380V, 50Hz, преко три фазна регулатора, као на слици. Угао паљења тиристора је α=90,
Microsoft Word - 4.Ucenik razlikuje direktno i obrnuto proporcionalne velicine, zna linearnu funkciju i graficki interpretira n
 4. UČENIK RAZLIKUJE DIREKTNO I OBRNUTO PROPORCIONALNE VELIČINE, ZNA LINEARNU FUNKCIJU I GRAFIČKI INTERPRETIRA NJENA SVOJSTVA U fajlu 4. iz srednjeg nivoa smo se upoznali sa postupkom rada kada je u pitanju
4. UČENIK RAZLIKUJE DIREKTNO I OBRNUTO PROPORCIONALNE VELIČINE, ZNA LINEARNU FUNKCIJU I GRAFIČKI INTERPRETIRA NJENA SVOJSTVA U fajlu 4. iz srednjeg nivoa smo se upoznali sa postupkom rada kada je u pitanju
Microsoft Word - GRAFICI TRIGONOMETRIJSKIH FUNKCIJA-II deo.doc
 GRAFICI TRIGONOMETRIJSKIH FUNKCIJA (II deo U prethodnom fajlu ( grafici trigonometrijskih funkcija I deo smo proučili kako se crtaju grafici u zavisnosti od brojeva a,b i c. Sada možemo sklopiti i ceo
GRAFICI TRIGONOMETRIJSKIH FUNKCIJA (II deo U prethodnom fajlu ( grafici trigonometrijskih funkcija I deo smo proučili kako se crtaju grafici u zavisnosti od brojeva a,b i c. Sada možemo sklopiti i ceo
Рачунарска интелигенција
 Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
PowerPoint Presentation
 Prof. dr Pere Tumbas Prof. dr Predrag Matkovid Identifikacija i izbor projekata Održavanje sistema Inicijalizacija projekata i planiranje Implementacija sistema Dizajn sistema Analiza sistema Faze životnog
Prof. dr Pere Tumbas Prof. dr Predrag Matkovid Identifikacija i izbor projekata Održavanje sistema Inicijalizacija projekata i planiranje Implementacija sistema Dizajn sistema Analiza sistema Faze životnog
Microsoft Word - KVADRATNA FUNKCIJA.doc
 KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b+ c Gde je R, a i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b+ c je parabola. Najpre ćemo naučiti kako izgleda
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b+ c Gde je R, a i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b+ c je parabola. Najpre ćemo naučiti kako izgleda
KATALOG ZNANJA IZ INFORMATIKE
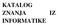 KATALOG ZNANJA IZ INFORMATIKE Nacionalni savjet za obrazovanje je na 27. sjednici održanoj 17. marta 2014. godine utvrdio izmjene predmetnoga programa INFORMATIKA za I razred gimnazije. Na zahtijev Pedagoško-psihološke
KATALOG ZNANJA IZ INFORMATIKE Nacionalni savjet za obrazovanje je na 27. sjednici održanoj 17. marta 2014. godine utvrdio izmjene predmetnoga programa INFORMATIKA za I razred gimnazije. Na zahtijev Pedagoško-psihološke
Алгебарски изрази 1. Запиши пет произвољних бројевних израза. 2. Израчунај вредност израза: а) : ; б) : (
 Алгебарски изрази 1. Запиши пет произвољних бројевних израза. 2. Израчунај вредност израза: а) 5 3 4 : 2 1 2 + 1 1 6 2 3 4 ; б) 5 3 4 : ( 2 1 2 + 1 1 6 ) 2 3 4 ; в) ( 5 3 4 : 2 1 2 + 1 1 6 ) 2 3 4 ; г)
Алгебарски изрази 1. Запиши пет произвољних бројевних израза. 2. Израчунај вредност израза: а) 5 3 4 : 2 1 2 + 1 1 6 2 3 4 ; б) 5 3 4 : ( 2 1 2 + 1 1 6 ) 2 3 4 ; в) ( 5 3 4 : 2 1 2 + 1 1 6 ) 2 3 4 ; г)
(Microsoft Word - Dr\236avna matura - studeni osnovna razina - rje\232enja)
 1. C. Imamo redom: I. ZADATCI VIŠESTRUKOGA IZBORA 9 + 7 6 9 + 4 51 = = = 5.1 18 4 18 8 10. B. Pomoću kalkulatora nalazimo 10 1.5 = 63.45553. Četvrta decimala je očito jednaka 5, pa se zaokruživanje vrši
1. C. Imamo redom: I. ZADATCI VIŠESTRUKOGA IZBORA 9 + 7 6 9 + 4 51 = = = 5.1 18 4 18 8 10. B. Pomoću kalkulatora nalazimo 10 1.5 = 63.45553. Četvrta decimala je očito jednaka 5, pa se zaokruživanje vrši
Школа Ј. Ј. Змај Свилајнац МЕСЕЧНИ ПЛАН РАДА ЗА СЕПТЕМБАР Школска 2018 /2019. Назив предмета: Информатика и рачунарство Разред: 5. Недељни број часова
 Школа Ј. Ј. Змај Свилајнац МЕСЕЧНИ ПЛАН РАДА ЗА СЕПТЕМБАР јединице 1. 1. Увод у информатику и рачунарство 1. 2. Oрганизација података на рачунару 1. 3. Рад са текстуалним документима 1. 4. Форматирање
Школа Ј. Ј. Змај Свилајнац МЕСЕЧНИ ПЛАН РАДА ЗА СЕПТЕМБАР јединице 1. 1. Увод у информатику и рачунарство 1. 2. Oрганизација података на рачунару 1. 3. Рад са текстуалним документима 1. 4. Форматирање
No Slide Title
 Statistika je skup metoda za uređivanje, analiziranje i grafičko prikazivanje podataka. statistika???? Podatak je kvantitativna ili kvalitativna vrijednost kojom je opisano određeno obilježje (svojstvo)
Statistika je skup metoda za uređivanje, analiziranje i grafičko prikazivanje podataka. statistika???? Podatak je kvantitativna ili kvalitativna vrijednost kojom je opisano određeno obilježje (svojstvo)
1. GRUPA Pismeni ispit iz MATEMATIKE Prezime i ime broj indeksa 1. (15 poena) Rexiti matriqnu jednaqinu 3XB T + XA = B, pri qemu
 1. GRUPA Pismeni ispit iz MATEMATIKE 1 0.0.01. Prezime i ime broj indeksa 1. (15 poena) Rexiti matriqnu jednaqinu XB T + XA = B, 1 4 pri qemu je A = 6 9 i B = 1 1 0 1 1. 4 4 4 8 1. Data je prava q : {
1. GRUPA Pismeni ispit iz MATEMATIKE 1 0.0.01. Prezime i ime broj indeksa 1. (15 poena) Rexiti matriqnu jednaqinu XB T + XA = B, 1 4 pri qemu je A = 6 9 i B = 1 1 0 1 1. 4 4 4 8 1. Data je prava q : {
POSLOVNI INFORMACIONI SISTEMI I RA^UNARSKE
 ZNAČAJ RAČUNARSKIH KOMUNIKACIJA U BANKARSKOM POSLOVANJU RAČUNARSKE MREŽE Računarske mreže su nastale kombinacijom računara i telekomunikacija dve tehnologije sa veoma različitom tradicijom i istorijom.
ZNAČAJ RAČUNARSKIH KOMUNIKACIJA U BANKARSKOM POSLOVANJU RAČUNARSKE MREŽE Računarske mreže su nastale kombinacijom računara i telekomunikacija dve tehnologije sa veoma različitom tradicijom i istorijom.
Vjezbe 1.dvi
 Matematia I Elvis Baraović 0 listopada 08 Prirodno-matematiči faultet Univerziteta u Tuzli, Odsje matematia, Univerzitetsa 75000 Tuzla;http://pmfuntzba/staff/elvisbaraovic/ Sadržaj Sup realnih brojeva
Matematia I Elvis Baraović 0 listopada 08 Prirodno-matematiči faultet Univerziteta u Tuzli, Odsje matematia, Univerzitetsa 75000 Tuzla;http://pmfuntzba/staff/elvisbaraovic/ Sadržaj Sup realnih brojeva
Microsoft Word - 13pavliskova
 ПОДЗЕМНИ РАДОВИ 4 (5) 75-8 UDK 6 РУДАРСКО-ГЕОЛОШКИ ФАКУЛТЕТ БЕОГРАД YU ISSN 5494 ИЗВОД Стручни рад УПОТРЕБА ОДВОЈЕНОГ МОДЕЛА РЕГЕНЕРАЦИЈЕ ЗА ОДРЕЂИВАЊЕ ПОУЗДАНОСТИ ТРАНСПОРТНЕ ТРАКЕ Павлисковá Анна, Марасовá
ПОДЗЕМНИ РАДОВИ 4 (5) 75-8 UDK 6 РУДАРСКО-ГЕОЛОШКИ ФАКУЛТЕТ БЕОГРАД YU ISSN 5494 ИЗВОД Стручни рад УПОТРЕБА ОДВОЈЕНОГ МОДЕЛА РЕГЕНЕРАЦИЈЕ ЗА ОДРЕЂИВАЊЕ ПОУЗДАНОСТИ ТРАНСПОРТНЕ ТРАКЕ Павлисковá Анна, Марасовá
Microsoft Word - AIDA2kolokvijumRsmerResenja.doc
 Konstrukcija i analiza algoritama 2 (prvi kolokvijum, smer R) 1. a) Konstruisati AVL stablo od brojeva 100, 132, 134, 170, 180, 112, 188, 184, 181, 165 (2 poena) b) Konkatenacija je operacija nad dva skupa
Konstrukcija i analiza algoritama 2 (prvi kolokvijum, smer R) 1. a) Konstruisati AVL stablo od brojeva 100, 132, 134, 170, 180, 112, 188, 184, 181, 165 (2 poena) b) Konkatenacija je operacija nad dva skupa
Slide 1
 Merni sistemi u računarstvu, http://automatika.etf.rs/sr/13e053msr Merna nesigurnost tipa A doc. dr Nadica Miljković, kabinet 68, nadica.miljkovic@etf.rs Prezentacija za ovo predavanje je skoro u potpunosti
Merni sistemi u računarstvu, http://automatika.etf.rs/sr/13e053msr Merna nesigurnost tipa A doc. dr Nadica Miljković, kabinet 68, nadica.miljkovic@etf.rs Prezentacija za ovo predavanje je skoro u potpunosti
УНИВЕРЗИТЕТ У НИШУ ПРИРОДНО-МАТЕМАТИЧКИ ФАКУЛТЕТ Департман за рачунарске науке Писмени део испита из предмета Увод у рачунарство 1. [7 пое
 УНИВЕРЗИТЕТ У НИШУ ПРИРОДНО-МАТЕМАТИЧКИ ФАКУЛТЕТ Департман за рачунарске науке 30.06.2018. Писмени део испита из предмета Увод у рачунарство 1. [7 поена] Методом МакКласкија минимизарити систем прекидачких
УНИВЕРЗИТЕТ У НИШУ ПРИРОДНО-МАТЕМАТИЧКИ ФАКУЛТЕТ Департман за рачунарске науке 30.06.2018. Писмени део испита из предмета Увод у рачунарство 1. [7 поена] Методом МакКласкија минимизарити систем прекидачких
Динамика крутог тела
 Динамика крутог тела. Задаци за вежбу 1. Штап масе m и дужине L се крајем А наслања на храпаву хоризонталну раван, док на другом крају дејствује сила F константног интензитета и правца нормалног на штап.
Динамика крутог тела. Задаци за вежбу 1. Штап масе m и дужине L се крајем А наслања на храпаву хоризонталну раван, док на другом крају дејствује сила F константног интензитета и правца нормалног на штап.
ФАКУЛТЕТ ОРГАНИЗАЦИОНИХ НАУКА
 Питања за усмени део испита из Математике 3 I. ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ 1. Појам диференцијалне једначине. Пикарова теорема. - Написати општи и нормални облик диференцијалне једначине првог реда. - Дефинисати:
Питања за усмени део испита из Математике 3 I. ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ 1. Појам диференцијалне једначине. Пикарова теорема. - Написати општи и нормални облик диференцијалне једначине првог реда. - Дефинисати:
P9.1 Dodela resursa, Bojenje grafa
 Фаза доделе ресурса Ова фаза се у литератури назива и фазом доделе регистара, при чему се под регистрима подразумева скуп ресурса истог типа. Додела регистара променљивама из графа сметњи се обавља тзв.
Фаза доделе ресурса Ова фаза се у литератури назива и фазом доделе регистара, при чему се под регистрима подразумева скуп ресурса истог типа. Додела регистара променљивама из графа сметњи се обавља тзв.
PITANJA I ZADACI ZA II KOLOKVIJUM IZ MATEMATIKE I Pitanja o nizovima Nizovi Realni niz i njegov podniz. Tačka nagomilavanja niza i granična vrednost(l
 PITANJA I ZADACI ZA II KOLOKVIJUM IZ MATEMATIKE I Pitanja o nizovima Nizovi Realni niz i njegov podniz. Tačka nagomilavanja niza i granična vrednost(limes) niza. Svojstva konvergentnih nizova, posebno
PITANJA I ZADACI ZA II KOLOKVIJUM IZ MATEMATIKE I Pitanja o nizovima Nizovi Realni niz i njegov podniz. Tačka nagomilavanja niza i granična vrednost(limes) niza. Svojstva konvergentnih nizova, posebno
Београд, МАТРИЧНА АНАЛИЗА КОНСТРУКЦИЈА ЗАДАТАК 1 За носач приказан на слици: а) одредити дужине извијања свих штапова носача, ако на носач
 Београд, 30.01.2016. а) одредити дужине извијања свих штапова носача, ако на носач делују само концентрисане силе, б) ако је P = 0.8P cr, и на носач делује расподељено оптерећење f, одредити моменат савијања
Београд, 30.01.2016. а) одредити дужине извијања свих штапова носача, ако на носач делују само концентрисане силе, б) ако је P = 0.8P cr, и на носач делује расподељено оптерећење f, одредити моменат савијања
Konstrukcija i analiza algoritama Nina Radojičić februar Analiza algoritama, rekurentne relacije 1 Definicija: Neka su f i g dve pozitivne fun
 Konstrukcija i analiza algoritama Nina Radojičić februar 2018. 1 Analiza algoritama, rekurentne relacije 1 Definicija: Neka su f i g dve pozitivne funkcije od argumenta n iz skupa N prirodnih brojeva.
Konstrukcija i analiza algoritama Nina Radojičić februar 2018. 1 Analiza algoritama, rekurentne relacije 1 Definicija: Neka su f i g dve pozitivne funkcije od argumenta n iz skupa N prirodnih brojeva.
PRIRODNO-MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA MATEMATIKU I INFORMATIKU ZADACI SA REŠENJIMA SA PRIJEMNOG ISPITA IZ MATEMATIKE, JUN Odrediti
 PRIRODNO-MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA MATEMATIKU I INFORMATIKU ZADACI SA REŠENJIMA SA PRIJEMNOG ISPITA IZ MATEMATIKE, JUN 0. Odrediti moduo kompleksnog broja Rešenje: Uočimo da važi z = + i00
PRIRODNO-MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA MATEMATIKU I INFORMATIKU ZADACI SA REŠENJIMA SA PRIJEMNOG ISPITA IZ MATEMATIKE, JUN 0. Odrediti moduo kompleksnog broja Rešenje: Uočimo da važi z = + i00
PROMENLJIVE, TIPOVI PROMENLJIVIH
 PROMENLJIVE, TIPOVI PROMENLJIVIH Šta je promenljiva? To je objekat jezika koji ima ime i kome se mogu dodeljivati vrednosti. Svakoj promenljivoj se dodeljuje registar (memorijska lokacija) operativne memorije
PROMENLJIVE, TIPOVI PROMENLJIVIH Šta je promenljiva? To je objekat jezika koji ima ime i kome se mogu dodeljivati vrednosti. Svakoj promenljivoj se dodeljuje registar (memorijska lokacija) operativne memorije
УНИВЕРЗИТЕТ У БЕОГРАДУ МАШИНСКИ ФАКУЛТЕТ Предмет: КОМПЈУТЕРСКА СИМУЛАЦИЈА И ВЕШТАЧКА ИНТЕЛИГЕНЦИЈА Задатак број: Лист/листова: 1/1 Задатак 5.1 Pостоје
 Лист/листова: 1/1 Задатак 5.1 Pостоје софтвери за препознавање бар кодова који знатно олакшавају велики број операција које захтевају препознавање објеката. Слика 1: Приказ свих слова за које је ART-1
Лист/листова: 1/1 Задатак 5.1 Pостоје софтвери за препознавање бар кодова који знатно олакшавају велики број операција које захтевају препознавање објеката. Слика 1: Приказ свих слова за које је ART-1
ALIP1_udzb_2019.indb
 Razmislimo Kako u memoriji računala prikazujemo tekst, brojeve, slike? Gdje se spremaju svi ti podatci? Kako uopće izgleda memorija računala i koji ju elektronički sklopovi čine? Kako biste znali odgovoriti
Razmislimo Kako u memoriji računala prikazujemo tekst, brojeve, slike? Gdje se spremaju svi ti podatci? Kako uopće izgleda memorija računala i koji ju elektronički sklopovi čine? Kako biste znali odgovoriti
Microsoft Word - Novi proizvod - Sistem za komunikaciju 720 v1.doc
 ТЕХНИЧКО РЕШЕЊЕ Нови производ: Једносмерна дистрибуција напона као оптимално решење коришћења енергије алтернативних извора Руководилац пројекта: Живанов Љиљана Одговорно лице: Лазић Мирослав Аутори: Лазић
ТЕХНИЧКО РЕШЕЊЕ Нови производ: Једносмерна дистрибуција напона као оптимално решење коришћења енергије алтернативних извора Руководилац пројекта: Живанов Љиљана Одговорно лице: Лазић Мирослав Аутори: Лазић
Kvadrupolni maseni analizator, princip i primena u kvali/kvanti hromatografiji
 Kvadrupolni maseni analizator, princip i primena u kvali/kvanti hromatografiji doc dr Nenad Vuković, Institut za hemiju, Prirodno-matematički fakultet u Kragujevcu JONIZACIJA ELEKTRONSKIM UDAROM Joni u
Kvadrupolni maseni analizator, princip i primena u kvali/kvanti hromatografiji doc dr Nenad Vuković, Institut za hemiju, Prirodno-matematički fakultet u Kragujevcu JONIZACIJA ELEKTRONSKIM UDAROM Joni u
EНЕРГЕТСКИ ПРЕТВАРАЧИ 1 јануар Трофазни једнострани исправљач прикључен је на круту мрежу 3x380V, 50Hz преко трансформатора у спрези Dy, као
 EНЕРГЕТСКИ ПРЕТВАРАЧИ 1 јануар 017. 1. Трофазни једнострани исправљач прикључен је на круту мрежу x80, 50Hz преко трансформатора у спрези Dy, као на слици 1. У циљу компензације реактивне снаге, паралелно
EНЕРГЕТСКИ ПРЕТВАРАЧИ 1 јануар 017. 1. Трофазни једнострани исправљач прикључен је на круту мрежу x80, 50Hz преко трансформатора у спрези Dy, као на слици 1. У циљу компензације реактивне снаге, паралелно
Microsoft Word - pitalice.doc
 NAPOMENA!!! Ako su ponuđeni odgovori na neke od pitalica, molim sve da to ne uzimaju zdravo za gotovo, nego da provere. Sve duplikate pitalica ignorišite! :) 3. Diskretizacija signala u vremenu. Teorema
NAPOMENA!!! Ako su ponuđeni odgovori na neke od pitalica, molim sve da to ne uzimaju zdravo za gotovo, nego da provere. Sve duplikate pitalica ignorišite! :) 3. Diskretizacija signala u vremenu. Teorema
ЗАДАЦИ ИЗ МАТЕМАТИКЕ ЗА ПРИПРЕМАЊЕ ЗАВРШНОГ ИСПИТА
 ЗАДАЦИ ИЗ МАТЕМАТИКЕ ЗА ПРИПРЕМАЊЕ ЗАВРШНОГ ИСПИТА p m m m Дат је полином ) Oдредити параметар m тако да полином p буде дељив са б) Одредити параметар m тако да остатак при дељењу p са буде једнак 7 а)
ЗАДАЦИ ИЗ МАТЕМАТИКЕ ЗА ПРИПРЕМАЊЕ ЗАВРШНОГ ИСПИТА p m m m Дат је полином ) Oдредити параметар m тако да полином p буде дељив са б) Одредити параметар m тако да остатак при дељењу p са буде једнак 7 а)
Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]
![Microsoft PowerPoint - 03-Slozenost [Compatibility Mode] Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]](/thumbs/102/154806426.jpg) Сложеност алгоритама (Програмирање 2, глава 3, глава 4-4.3) Проблем: класа задатака истог типа Велики број различитих (коректних) алгоритама Величина (димензија) проблема нпр. количина података које треба
Сложеност алгоритама (Програмирање 2, глава 3, глава 4-4.3) Проблем: класа задатака истог типа Велики број различитих (коректних) алгоритама Величина (димензија) проблема нпр. количина података које треба
Microsoft Word - ASIMPTOTE FUNKCIJE.doc
 ASIMPTOTE FUNKCIJE (PONAŠANJE FUNKCIJE NA KRAJEVIMA OBLASTI DEFINISANOSTI) Ovo je jedna od najznačajnijih tačaka u ispitivanju toka funkcije. Neki profesori zahtevaju da se asimptote rade kao. tačka u
ASIMPTOTE FUNKCIJE (PONAŠANJE FUNKCIJE NA KRAJEVIMA OBLASTI DEFINISANOSTI) Ovo je jedna od najznačajnijih tačaka u ispitivanju toka funkcije. Neki profesori zahtevaju da se asimptote rade kao. tačka u
Microsoft PowerPoint - DAC.ppt [Compatibility Mode]
![Microsoft PowerPoint - DAC.ppt [Compatibility Mode] Microsoft PowerPoint - DAC.ppt [Compatibility Mode]](/thumbs/100/145818915.jpg) Analogne i digitalne velicine Analogne veličine su kontinualne po vremenu i amplitudi. Digitalne veličine se predstavljaju nizom brojeva. Svaki broj predstavlja jedan odbirak u vremenu. Odbirak ima konačnu
Analogne i digitalne velicine Analogne veličine su kontinualne po vremenu i amplitudi. Digitalne veličine se predstavljaju nizom brojeva. Svaki broj predstavlja jedan odbirak u vremenu. Odbirak ima konačnu
My_P_Trigo_Zbir_Free
 Штa треба знати пре почетка решавања задатака? ТРИГОНОМЕТРИЈА Ниво - Основне формуле које произилазе из дефиниција тригонометријских функција Тригонометријске функције се дефинишу у правоуглом троуглу
Штa треба знати пре почетка решавања задатака? ТРИГОНОМЕТРИЈА Ниво - Основне формуле које произилазе из дефиниција тригонометријских функција Тригонометријске функције се дефинишу у правоуглом троуглу
Рационални Бројеви Скуп рационалних бројева 1. Из скупа { 3 4, 2, 4, 11, 0, , 1 5, 12 3 } издвој подскуп: а) природних бројева; б) целих броје
 Рационални Бројеви Скуп рационалних бројева. Из скупа {,,,, 0,,, } издвој подскуп: а) природних бројева; б) целих бројева; в) ненегативних рационалних бројева; г) негативних рационалних бројева.. Запиши
Рационални Бројеви Скуп рационалних бројева. Из скупа {,,,, 0,,, } издвој подскуп: а) природних бројева; б) целих бројева; в) ненегативних рационалних бројева; г) негативних рационалних бројева.. Запиши
