Microsoft PowerPoint - SamoorganizirajuceNN_2
|
|
|
- Francka Zupan
- пре 5 година
- Прикази:
Транскрипт
1 Neformaln uvod Samoorganzrajuće neuronske mreže Prof. dr.sc. Bojana Dalbelo-Bašć Marko Čupć, dpl. ng. FER Zagreb Kako uče neuronske mreže? Učenje s učteljem (supervsed learnng) Tpčan prmjer je FF-ANN Backpropagaton algortam učenja Karakterstke: poznat su ulaz odgovarajuć zlaz; mreža uč preslkavanje ulaz-zlaz Učenje bez učtelja (unsupervsed learnng) U suprotnost s konceptom učenja? Zapravo ne. Evo deje Neformaln uvod X X Malo dete nalaz se na pustom otoku Vd oko sebe razlčte žvotnje uč Y Y X Z Z 3 4 Neformaln uvod Što dete uč? Postoj X koj ma sljedeće karakterstke: Malo je, let Postoj Y koj ma sljedeće karakterstke: Zadržava se na kopnu, hoda l poskakuje, Postoj Z koj ma sljedeće karakterstke: Malo je, plva, ne napušta vodu Neformaln uvod Dete obavlja klasterranje; uč bez učtelja M znamo da zapravo vred: X je ptca Y je kopnena žvotnja Z je rba Učenje bez učtelja samoorganzaca: vrlo čest u prrod 5 6
2 Mehanzam natjecanja (S. Grossberg) optmzaca funkca elemenata dstrburanog sustava (društvo, bologa, računarsk sustav,...) Natjecanje - vod do optmzace na lokalnoj razn bez potrebe za globalnom kontrolom vrlo česta pojava u bolog Sv PE mreže dobvaju dentčan nput, al se natječu: Lateralnm vezama Formulacom prncpa učenja Specalzaca PE za određena područja ulaznog prostora oslkavanje strukture nputa Kod učenja NN specalzraju se PE na određen načn (tako da smanju pogrešku). Backpropagaton pogreške kod nelnearnh mreža vod specalzac neurona, al ndrektno uz velke troškove sporu konvergencu RBF se po svojoj prrod specalzraju, al područje se određuje unapred Kompettvne mreže specalzraju se postupkom natjecanja! 7 8 Četr zahtjeva na samoorganzrajuće NN Četr zahtjeva na samoorganzrajuće NN. Težnsk faktor u neuronu moraju bt predstavnc klase uzoraka, tako da svak neuron predstavlja drugu klasu.. Ulazn uzorak predstavlja se svm neuronma, svak neuron je zlazn. Vrednost zlaza je mjera slčnost zmeđu ulaznog uzorka uzorka pohranjenog u neuronu. 3. Korst se natjecateljska stratega učenja (engl. compettve learnng strategy) koja odabre neuron s najvećm zlazom. 4. Postoje metode potcanja najvećeg zlaza. 9 0 Podjele obzrom na tp natjecanja: Čvrsto natjecanje (eng. hard competto postoj samo jedan pobjednk, samo on uč Meko natjecanje (eng. soft competto postoj samo jedan pobjednk, al u određenoj mjer uče njegov susjed Tpčn predstavnk kompettvne NN sloj PE gdje sv dobvaju ste ulazne podatke PE sa najvećm (najmanjm) zlazom proglašava se pobjednkom Trvalna zvedba kod dgtalnh računala Nepoželjno: Treba postojat globaln nadzornk Preskupo za dstrburane sustave
3 mreža rješenje problema + y y y n + + N procesnh elemenata Samo onaj element PE za kojega x >x j j na zlazu daje, sv ostal 0 Postoj jednčna poztvna povratna veza elementa na samog sebe Postoje negatvne lateralne veze velčne ε (0 < ε < /N) na sve ostale procesne elemente Nakon prelaznog razdoblja zlaz se stablzra y y y n x x Čvrsto natjecanje Prmjer... 4 x x Mrež se u prvom trenutku predoč ulazn uzorak, zatm se makne Lateralne negatvne veze sve zlaze tjeraju eksponencalno prema nul PE s najvećm ulaznm uzorkom sve manje osjeća -ε veze, počnje ponovno rast (zbog + veze), još vše zaguš preostale procesne elemente Prmjer odzva dstrburane zvedbe WTA -sv PE rade ažurranje snkrono (postoje asnkrone verze) -Postoj prelazna pojava: 5 6 Prmjer mreže koja prmjenjuje kompettvno učenje Svak neuron specalzra se za jedno područje Korst se za klasfkacu, jer su zlaz y mreže bnarn (0/), tj. y = ako net >net j, za svak j, j y =0 nače 7 8 3
4 x x PE net y Metoda učenja (Grossberg) učenje bez učtelja (modfkaca Hebbovog učenja): w ( n + ) = w ( + η y ( ( x ( w ( ) j PE net y Odnosno vektorsk: w ( n + ) = w ( + η y ( ( x( w ( ) PE m net m y m Kohonenovo pravlo Ovaj član osgurava da uč samo pobjednk! 9 0 geometrska nterpretaca w ( n + ) = w ( + η y ( ( x( w ( ) 0 x r w r r x r w η x w ) ( Težnsk faktor postaju slčn ulaznm vrednostma! Na koj načn procesn element računa zlaz? Izlaz mora bt mjera slčnost sa predočenm uzorkom! Rješenje: računat mjeru kuta zmeđu uzorka na ulazu pohranjenog uzorka. ϕ x r w r cos ϕ = x w x w x w Komplcran račun (ako se ne aproksmra skalarnm produktom) Ako se korst aproksmaca, moguće pogreške Oba načna smanjuju mogućnost klasfkace uzoraka jer sve uzorke smještaju na obod jednčne hperkugle 3 Rješenje korstt udaljenost Eukldska udaljenost se korst češće r x r w = ( x k wk ) Pobjednk je onaj PE koj je najblž k prmjer 4 4
5 - prmjer Dva procesna elementa Kompettvna stratega učenja PE (plav) Uzorc za učenje (crne točkce) -generraju se u dva klastera Ukolko je nek PE daleko od klastera, nkada neće pobedt u natjecanju podest svoje težnske faktore mrtav PE! Rješenje problema: savjest Svak element udaljenost od ulaznog uzorka procjenjuje subjektvno Ako PE prečesto pobjeđuje, grze ga savjest pa mu se čn da je dalje, nego što stvarno jest. PE (crve 5 6 OUTSTAR mreža Savjest: udaljenost se povećava D( w, x) D( w, x) b b : duljna usled savjest (/N pravedn udo pobjede) b γ 0, 0 = γ c N c : procjena postotka pobjeđvanja c ( n + ) = c ( + β o ( c (, β 0.00 ( ) o : za pobjedu, 0 za poraz Onlne zvedba procjene svak PE računa zasebno prmjer 7 Slčna INSTAR mrež, međutm: Ulaz mreže su bnarn, to samo jedan ulaz može bt u. Na zlaze mreže se ne postavlja ogrančenje Izlaz je net Služ za replcranje pohranjenh uzoraka Za svak aktvan ulaz može se odredt što treba dat na zlazu 8 OUTSTAR mreža OUTSTAR mreža x x PE net y Pravlo učenja učenje s učteljem: w = w + η ( y w ) x Težnsk faktor postaju slčn zlaznm vrednostma! PE net y Poznato kao: Grossbergovo pravlo Vektorsk oblk: w = w + η j j r ( y w ) x j PE m net m y m Uč samo -t PE zbog x
6 INSTAR-OUTSTAR mreža INSTAR-OUTSTAR mreža Ovakav spoj mreže pokazuje vrlo zanmljvo svojstvo asocatvnost: z podataka sa šumom prepozna kojoj klas uzorak dosta prpada OUTSTAR mreža zatm na zlazu generra savršenog predstavnka te klase (odnosno uklanja šum) x x I N S T A R m r e ž a O U T S T A R m r e ž a net PE net PE net PE net PE y y net m net m y m PE m PE m 3 3 Meko natjecanje Čvrsto natjecanje uvek daje jednog pobjednka Kod mekog natjecanja zna se pobjednk, al uč njegova okolna Moguća također dstrburana zvedba Veze prema blskm susjedma su poztvne Veze prema daljm susjedma su negatve Meko natjecanje Meko natjecanje grad svojstvo susjednost Susjedn PE predstavljaju klastere koj su nače blzu Stvara se topološko mapranje Ako se dva ulaza preslkaju u PE koj su blzu, tada su ulazn uzorc blzu Čuva se dstrbuca podataka Najpoznat prmjer: Kohonenove samoorganzrajuće mape (SOM) Kohonenova SOM je potpuno povezana, lnearna jednoslojna mreža PE se tpčno povezuju u D lanac, l D polje X PE, PE, PE,3 PE,4 PE, PE, PE,3 PE,4 PE 3, PE 3, PE 3,3 PE 3,4 PE 4, PE 4, PE 4,3 PE 4,
7 Učenje SOMa: Funkca susjednost: ( x( w ( )) w ( n + ) = w ( + Λ * ( η( n, Λ d *, = exp σ ( * (, 37 Dve faze učenja:. Incalna faza. Stvara se grub poredak PEa. Stopu učenja treba držat vsokom, postupno smanjvat, od npr. 0.5 do 0.0, kroz N 0 =000 teraca n η( =η0( ) N + K 0 K je prozvoljna konst.- defnra krajnj η; broj terace n =, N 0 Susjedstvo treba smanjvat od pola mape prema samo jednom elementu n σ ( = σ 0 N0 38 Faze učenja:. Faza konvergence. Fno se podešavaju PE. Susjedstvo treba ogrančt na najblže, l čak na sam PE, a stopu učenja treba smanjvat od 0.0 prema 0. Trajanje je 0-00 puta dulje od ncalne faze. - prmjer Klasčn pogled na procesne elemente generrane uzorke. Prmjer KohD, KohD prmjer Lnama su povezan susjedn procesn element. Što je zlaz ove mreže? Dva skupa težna jedan za natjecanje, a drug za određvanje zlaza Postupak natjecanja provod grupranje (clusterng) a ne klasfkacu! 4 4 7
8 Counterpropagaton mreža Prmjer uporabe SOM-a Općent nazv za blo koju mrežu sastavljenu z dva dela:. Kompettvnog ulaznog dela koj vrš klasterranje. Izlaznog dela koj se uč metodom učenja s učteljem INSTAR-OUTSTAR mreža je mreža ovog tpa Učenje tpčno u dve faze:. faza: učenje samoorganzrajućeg dela (učenje bez učtelja). faza: učenje feedforward mreže (učenje s učteljem) 43 Prepoznavanje govora Kohonen: Phonetc typewrter for the Fnnsh language Ulaz: govor Izlaz: psan tekst Arhtektura: D polje od 96 PE-a Svak PE dobva na 5 ulaza delove spektra govora Nakon procesa samoorganzace uočava se grupranje slčnh verza stog fonema Prepoznavanje: praćenje trajektore 44 Lteratura Prncpe, Lefebvre, and Eulano: Neural Systems: Fundamentals Through Smulatons N. K. Bose, P. Lang: Neural Network Fundamentals wth Graphs, Algorthms, and Applcatons, McGraw-Hll,
1. KOLOKVIJ IZ MATEMATIKE I, PRVI DIO - GRUPA A 24. listopada (i) Napi²ite formulu za determinantu i inverz op e matrice drugog reda, te nave
 1 KOLOKVIJ IZ MATEMATIKE I, PRVI DIO - GRUPA A 4 lstopada 011 1 () Nap²te formulu a determnantu nver op e matrce drugog reda, te navedte uvjet ( ) 3 7 1 11 1 3 () Provjerte je l matrca B = 1 3 1 5 nverna
1 KOLOKVIJ IZ MATEMATIKE I, PRVI DIO - GRUPA A 4 lstopada 011 1 () Nap²te formulu a determnantu nver op e matrce drugog reda, te navedte uvjet ( ) 3 7 1 11 1 3 () Provjerte je l matrca B = 1 3 1 5 nverna
MARKOVLJEVI LANCI Prvi kolokvij 28. studenog Zadatak 1. (a) (5 bodova) Za Markovljev lanac (X n ) i njegovo stanje i S neka T (n) i u stanje i.
 Zadatak. (a) (5 bodova) Za Markovljev lanac (X n ) njegovo stanje S neka T (n) u stanje. Dokaºte da za svak n N vrjed P (T (n) < ) = f n, ozna ava n-to vrjeme povratka pr emu je f := P (T () < ). (Napomena:
Zadatak. (a) (5 bodova) Za Markovljev lanac (X n ) njegovo stanje S neka T (n) u stanje. Dokaºte da za svak n N vrjed P (T (n) < ) = f n, ozna ava n-to vrjeme povratka pr emu je f := P (T () < ). (Napomena:
УНИВЕРЗИТЕТ У БЕОГРАДУ МАШИНСКИ ФАКУЛТЕТ Предмет: КОМПЈУТЕРСКА СИМУЛАЦИЈА И ВЕШТАЧКА ИНТЕЛИГЕНЦИЈА Задатак број: Лист/листова: 1/1 Задатак 5.1 Pостоје
 Лист/листова: 1/1 Задатак 5.1 Pостоје софтвери за препознавање бар кодова који знатно олакшавају велики број операција које захтевају препознавање објеката. Слика 1: Приказ свих слова за које је ART-1
Лист/листова: 1/1 Задатак 5.1 Pостоје софтвери за препознавање бар кодова који знатно олакшавају велики број операција које захтевају препознавање објеката. Слика 1: Приказ свих слова за које је ART-1
Microsoft Word Q19-078
 . Naučno-stručn skup sa međunarodnm učešćem QUALIY 209, Neum, B&H, 4-6 jun 209. SEPENI MODEL REGRESIJE: ODREĐIVANJE KOEFICIJENAA MODELA POWER REGRESSION MODEL: PARAMEERS DEERMINAION Alma Žga, Dr. Sc. Anel
. Naučno-stručn skup sa međunarodnm učešćem QUALIY 209, Neum, B&H, 4-6 jun 209. SEPENI MODEL REGRESIJE: ODREĐIVANJE KOEFICIJENAA MODELA POWER REGRESSION MODEL: PARAMEERS DEERMINAION Alma Žga, Dr. Sc. Anel
Microsoft Word - Trigonometrijski oblik kompleksnog broja.doc
 Trgonometrjsk oblk kompleksnog broja Da se podsetmo: Kompleksn broj je oblka je realn deo, je magnarn deo kompleksnog broja, - je magnarna jednca, ( Dva kompleksna broja su jednaka ako je Za broj _ je
Trgonometrjsk oblk kompleksnog broja Da se podsetmo: Kompleksn broj je oblka je realn deo, je magnarn deo kompleksnog broja, - je magnarna jednca, ( Dva kompleksna broja su jednaka ako je Za broj _ je
POSLOVNI INFORMACIONI SISTEMI I RA^UNARSKE
 ZNAČAJ RAČUNARSKIH KOMUNIKACIJA U BANKARSKOM POSLOVANJU RAČUNARSKE MREŽE Računarske mreže su nastale kombinacijom računara i telekomunikacija dve tehnologije sa veoma različitom tradicijom i istorijom.
ZNAČAJ RAČUNARSKIH KOMUNIKACIJA U BANKARSKOM POSLOVANJU RAČUNARSKE MREŽE Računarske mreže su nastale kombinacijom računara i telekomunikacija dve tehnologije sa veoma različitom tradicijom i istorijom.
Klasifikacija slika kucnih brojeva dubokim konvolucijskim modelima
 Klasifikacija slika kućnih brojeva dubokim konvolucijskim modelima Ivan Šego 4. srpnja 2018. Sadržaj 1 Uvod 2 Konvolucijske neuronske mreže Konvolucijski sloj Sloj sažimanja Potpuno povezani sloj 3 Ispitni
Klasifikacija slika kućnih brojeva dubokim konvolucijskim modelima Ivan Šego 4. srpnja 2018. Sadržaj 1 Uvod 2 Konvolucijske neuronske mreže Konvolucijski sloj Sloj sažimanja Potpuno povezani sloj 3 Ispitni
Microsoft Word - STO_VALJA_ZAPAMTITI_11.doc
 EHANIKA FLUIDA I Što valja zapamtt 40 Zaon očuvanja momenta olčne gbanja Dencja zaona očuvanja momenta olčne gbanja za materjaln volumen: Brzna promjene momenta olčne gbanja materjalnog volumena jednaa
EHANIKA FLUIDA I Što valja zapamtt 40 Zaon očuvanja momenta olčne gbanja Dencja zaona očuvanja momenta olčne gbanja za materjaln volumen: Brzna promjene momenta olčne gbanja materjalnog volumena jednaa
Microsoft Word - diplomski1.doc
 SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA DIPLOMSKI RAD br. 1633 Zaštta teksta dgtalnm vodenm žgom Thana Poljak Vodtelj: Marn Golub Zagreb, studen, 2007 1. Uvod U današnje vrjeme postoj
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA DIPLOMSKI RAD br. 1633 Zaštta teksta dgtalnm vodenm žgom Thana Poljak Vodtelj: Marn Golub Zagreb, studen, 2007 1. Uvod U današnje vrjeme postoj
ПА-4 Машинско учење-алгоритми машинског учења
 ПА-4 Машинско учење-алгоритми машинског учења Машинско учење увод и основни појмови Деф: the desgn and development of algorthms that allow computers to mprove ther performance over tme based on data sensor
ПА-4 Машинско учење-алгоритми машинског учења Машинско учење увод и основни појмови Деф: the desgn and development of algorthms that allow computers to mprove ther performance over tme based on data sensor
Sveučilište u Zagrebu
 SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA SEMINAR Osnovna svojstva kompleksnh mreža njhova prmjena Đan Glavnć 1.02 Vodtelj: Mr.sc. Mle Škć Zagreb, 05, 2007. Sadržaj 1. Uvod...1 2. Uvod
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA SEMINAR Osnovna svojstva kompleksnh mreža njhova prmjena Đan Glavnć 1.02 Vodtelj: Mr.sc. Mle Škć Zagreb, 05, 2007. Sadržaj 1. Uvod...1 2. Uvod
Microsoft Word - 3. G Markovic D Teodorovic.doc
 XXVII Smpozjum o novm tehnologjama u poštanskom telekomunkaconom saobraćaju PosTel 29, Beograd, 5.. decembar 29. PROBLEM LOCIRANJA ČVOROVA SA KONVERZIJOM TALASNIH DUŽINA U OPTIČKIM TRANSPORTNIM MREŽAMA
XXVII Smpozjum o novm tehnologjama u poštanskom telekomunkaconom saobraćaju PosTel 29, Beograd, 5.. decembar 29. PROBLEM LOCIRANJA ČVOROVA SA KONVERZIJOM TALASNIH DUŽINA U OPTIČKIM TRANSPORTNIM MREŽAMA
DIGITALNA OBRADA SIGNALA
 DIGITALNA OBRADA GOVORA U MOBILNOJ TELEFONIJI Parametr dgtalnh audo-sgnala Zvuk predstavlja brze promene vazdušnog prtska Ove promene regstrujemo ako su dovoljnog ntenzteta u odgovarajudem frekvencjskom
DIGITALNA OBRADA GOVORA U MOBILNOJ TELEFONIJI Parametr dgtalnh audo-sgnala Zvuk predstavlja brze promene vazdušnog prtska Ove promene regstrujemo ako su dovoljnog ntenzteta u odgovarajudem frekvencjskom
I колоквијум из Основа рачунарске технике I СИ- 2017/2018 ( ) Р е ш е њ е Задатак 1 Тачка А Потребно је прво пронаћи вредности функција f(x
 I колоквијум из Основа рачунарске технике I СИ- / (...) Р е ш е њ е Задатак Тачка А Потребно је прво пронаћи вредности функција f(x, x, x ) и g(x, x, x ) на свим векторима. f(x, x, x ) = x x + x x + x
I колоквијум из Основа рачунарске технике I СИ- / (...) Р е ш е њ е Задатак Тачка А Потребно је прво пронаћи вредности функција f(x, x, x ) и g(x, x, x ) на свим векторима. f(x, x, x ) = x x + x x + x
P9.1 Dodela resursa, Bojenje grafa
 Фаза доделе ресурса Ова фаза се у литератури назива и фазом доделе регистара, при чему се под регистрима подразумева скуп ресурса истог типа. Додела регистара променљивама из графа сметњи се обавља тзв.
Фаза доделе ресурса Ова фаза се у литератури назива и фазом доделе регистара, при чему се под регистрима подразумева скуп ресурса истог типа. Додела регистара променљивама из графа сметњи се обавља тзв.
Microsoft Word - SIORT1_2019_K1_resenje.docx
 I колоквијум из Основа рачунарске технике I СИ- 208/209 (24.03.209.) Р е ш е њ е Задатак f(x, x 2, x 3 ) = (x + x x ) x (x x 2 + x ) + x x 2 x 3 f(x, x 2, x 3 ) = (x + x x ) (x x + (x )) 2 + x + x x 2
I колоквијум из Основа рачунарске технике I СИ- 208/209 (24.03.209.) Р е ш е њ е Задатак f(x, x 2, x 3 ) = (x + x x ) x (x x 2 + x ) + x x 2 x 3 f(x, x 2, x 3 ) = (x + x x ) (x x + (x )) 2 + x + x x 2
Microsoft Word Potkorica.doc
 PREGLEDNI ČLANCI REVIEW PAPERS RADIO-LOCIRANJE MOBILNE STANICE U MREŽAMA TREĆE GENERACIJE Mlan M. Šunjevarć, Insttut za ssteme zasnovane na računarma RT-RK, Nov Sad, Srbja Mladen B. Veletć, Elektrotehnčk
PREGLEDNI ČLANCI REVIEW PAPERS RADIO-LOCIRANJE MOBILNE STANICE U MREŽAMA TREĆE GENERACIJE Mlan M. Šunjevarć, Insttut za ssteme zasnovane na računarma RT-RK, Nov Sad, Srbja Mladen B. Veletć, Elektrotehnčk
ELEKTRONIKA
 МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА РЕПУБЛИКЕ СРБИЈЕ ЗАЈЕДНИЦА ЕЛЕКТРОТЕХНИЧКИХ ШКОЛА РЕПУБЛИКЕ СРБИЈЕ ДВАДЕСЕТ ДРУГО РЕГИОНАЛНО ТАКМИЧЕЊЕ ЗАДАЦИ ИЗ ЕЛЕКТРОНИКЕ ЗА УЧЕНИКЕ ТРЕЋЕГ РАЗРЕДА
МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА РЕПУБЛИКЕ СРБИЈЕ ЗАЈЕДНИЦА ЕЛЕКТРОТЕХНИЧКИХ ШКОЛА РЕПУБЛИКЕ СРБИЈЕ ДВАДЕСЕТ ДРУГО РЕГИОНАЛНО ТАКМИЧЕЊЕ ЗАДАЦИ ИЗ ЕЛЕКТРОНИКЕ ЗА УЧЕНИКЕ ТРЕЋЕГ РАЗРЕДА
Увод у организацију и архитектуру рачунара 1
 Увод у организацију и архитектуру рачунара 2 Александар Картељ kartelj@matf.bg.ac.rs Напомена: садржај ових слајдова је преузет од проф. Саше Малкова Увод у организацију и архитектуру рачунара 2 1 Секвенцијалне
Увод у организацију и архитектуру рачунара 2 Александар Картељ kartelj@matf.bg.ac.rs Напомена: садржај ових слајдова је преузет од проф. Саше Малкова Увод у организацију и архитектуру рачунара 2 1 Секвенцијалне
Elektroenergetski sustav je zajedništvo: generatora, transformatora, vodova i trošila (potrošača)
 SEUČLŠTE U SPLTU Sveučlšn studjsk centar za stručne studje PREDNJ ZŠTT U ELETROENERGETSOM SUSTU Dr. sc. Petar Sarajčev, doc. Robert osor, dpl.ng. Sadržaj SDRŽJ 1. UOD... 1 1.1. ratak osvrt na elektroenergetsk
SEUČLŠTE U SPLTU Sveučlšn studjsk centar za stručne studje PREDNJ ZŠTT U ELETROENERGETSOM SUSTU Dr. sc. Petar Sarajčev, doc. Robert osor, dpl.ng. Sadržaj SDRŽJ 1. UOD... 1 1.1. ratak osvrt na elektroenergetsk
Projektovanje informacionih sistema i baze podataka
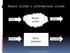 Realni sistem i informacioni sistem Ulaz Realni sistem Izlaz Unos Baza podataka Izveštaji Realni sistem i informacioni sistem Sistem se definiše kao skup objekata (entiteta) i njihovih međusobnih veza
Realni sistem i informacioni sistem Ulaz Realni sistem Izlaz Unos Baza podataka Izveštaji Realni sistem i informacioni sistem Sistem se definiše kao skup objekata (entiteta) i njihovih međusobnih veza
AV3-OE2-stručni PRIJELAZNE POJAVE Dr.sc. Venco Ćorluka 3. PRIJELAZNE POJAVE 3.1.Prijelazne pojave u mreži s otporom i induktivitetom Serijski spoj otp
 3. PIJAZN POJAV 3.1.Prjelazne pojave u mrež s oporom ndukveom Serjsk spoj opora ndukvea: Naponska jednadžba: ; d u u (3.1) Sruja kroz : 1e (3.) Napon na ndukveu: d u e (3.3) Napon na oporu: u u 1 e nergja
3. PIJAZN POJAV 3.1.Prjelazne pojave u mrež s oporom ndukveom Serjsk spoj opora ndukvea: Naponska jednadžba: ; d u u (3.1) Sruja kroz : 1e (3.) Napon na ndukveu: d u e (3.3) Napon na oporu: u u 1 e nergja
Poučak 56 Osnovna svojstva stabala i primjena na problem spajanja Jan Berger 1 i Mario Krnić 2 Prema bolonjskom načinu studiranja, studenti Fakulteta
 Poučak 56 Osnovna svojstva stabala prmjena na problem spajanja Jan Berger 1 Maro Krnć 2 Prema bolonjskom načnu studranja, student Fakulteta elektrotehnke računarstva završavaju preddplomsk studj takozvanm
Poučak 56 Osnovna svojstva stabala prmjena na problem spajanja Jan Berger 1 Maro Krnć 2 Prema bolonjskom načnu studranja, student Fakulteta elektrotehnke računarstva završavaju preddplomsk studj takozvanm
GEOMETRIJSKE KARAKTERISTIKE PRESEKA POPREČNOG PRESEKA GREDE PRIMERI
 OM V9 V0 me reme: ndex br: 8.6. EKSCENTRČNO NPREZNJE GREDE EKSCENTRČNO NPREZNJE GREDE PRMER PRMER. Za reseke rkaane na skc, nacrtat jegro reseka. ravougaon resek kružn resek OM V9 V0 me reme: ndex br:
OM V9 V0 me reme: ndex br: 8.6. EKSCENTRČNO NPREZNJE GREDE EKSCENTRČNO NPREZNJE GREDE PRMER PRMER. Za reseke rkaane na skc, nacrtat jegro reseka. ravougaon resek kružn resek OM V9 V0 me reme: ndex br:
MV Merchandise visibility sistem
 MV Merchandise visibility sistem Pomoć maloprodajnim lancima u smanjenju troškova usled nedostatka robe u prodajnom prostoru, smanjenju troškova i vremena za popis robe i povećanje prodaje Maloprodaje
MV Merchandise visibility sistem Pomoć maloprodajnim lancima u smanjenju troškova usled nedostatka robe u prodajnom prostoru, smanjenju troškova i vremena za popis robe i povećanje prodaje Maloprodaje
VIK-01 opis
 Višenamensko interfejsno kolo VIK-01 Višenamensko interfejsno kolo VIK-01 (slika 1) služi za povezivanje različitih senzora: otpornog senzora temperature, mernih traka u mostnoj vezi, termopara i dr. Pored
Višenamensko interfejsno kolo VIK-01 Višenamensko interfejsno kolo VIK-01 (slika 1) služi za povezivanje različitih senzora: otpornog senzora temperature, mernih traka u mostnoj vezi, termopara i dr. Pored
12-7 Use of the Regression Model for Prediction
 P r c e Pojam Aalza treda Sezoska cklča kompoeta Ideks brojev Vremeske serje Pojam Vremeske serje predstavljaju z mjereja jede promjeljve kroz vrjeme. Aalza vremeskh serja astoj da otkrje razumje regularost
P r c e Pojam Aalza treda Sezoska cklča kompoeta Ideks brojev Vremeske serje Pojam Vremeske serje predstavljaju z mjereja jede promjeljve kroz vrjeme. Aalza vremeskh serja astoj da otkrje razumje regularost
Logičke izjave i logičke funkcije
 Logičke izjave i logičke funkcije Građa računala, prijenos podataka u računalu Što su logičke izjave? Logička izjava je tvrdnja koja može biti istinita (True) ili lažna (False). Ako je u logičkoj izjavi
Logičke izjave i logičke funkcije Građa računala, prijenos podataka u računalu Što su logičke izjave? Logička izjava je tvrdnja koja može biti istinita (True) ili lažna (False). Ako je u logičkoj izjavi
Primjena neodredenog integrala u inženjerstvu Matematika 2 Erna Begović Kovač, Literatura: I. Gusić, Lekcije iz Matematike 2
 Primjena neodredenog integrala u inženjerstvu Matematika 2 Erna Begović Kovač, 2019. Literatura: I. Gusić, Lekcije iz Matematike 2 http://matematika.fkit.hr Uvod Ako su dvije veličine x i y povezane relacijom
Primjena neodredenog integrala u inženjerstvu Matematika 2 Erna Begović Kovač, 2019. Literatura: I. Gusić, Lekcije iz Matematike 2 http://matematika.fkit.hr Uvod Ako su dvije veličine x i y povezane relacijom
Stručno usavršavanje
 TOPLINSKI MOSTOVI IZRAČUN PO HRN EN ISO 14683 U organizaciji: TEHNIČKI PROPIS O RACIONALNOJ UPORABI ENERGIJE I TOPLINSKOJ ZAŠTITI U ZGRADAMA (NN 128/15, 70/18, 73/18, 86/18) dalje skraćeno TP Čl. 4. 39.
TOPLINSKI MOSTOVI IZRAČUN PO HRN EN ISO 14683 U organizaciji: TEHNIČKI PROPIS O RACIONALNOJ UPORABI ENERGIJE I TOPLINSKOJ ZAŠTITI U ZGRADAMA (NN 128/15, 70/18, 73/18, 86/18) dalje skraćeno TP Čl. 4. 39.
Neodreeni integrali - Predavanje III
 Neodredeni integrali Predavanje III Ines Radošević inesr@math.uniri.hr Odjel za matematiku Sveučilišta u Rijeci Neodredeni integrali Neodredeni integral Tablični integrali Metoda supstitucije Metoda parcijalne
Neodredeni integrali Predavanje III Ines Radošević inesr@math.uniri.hr Odjel za matematiku Sveučilišta u Rijeci Neodredeni integrali Neodredeni integral Tablični integrali Metoda supstitucije Metoda parcijalne
RED VOŽNJE ZA BESPLATAN PREVOZ LINIJA 1 UŠĆE TRG REPUBLIKE Polazno stajalište za ULAZ 6 kaplara za linije 16, 75, u smeru ka Zelenom vencu Krajn
 LINIJA 1 UŠĆE TRG REPUBLIKE Polazno stajalište za ULAZ za linije 16, 75, 83... u smeru ka Zelenom vencu Krajnje ULAZNO-IZLAZNO stajalište Trg Republike za linije 43, 96, 32E... SMER TRG REPUBLIKE - UŠĆE
LINIJA 1 UŠĆE TRG REPUBLIKE Polazno stajalište za ULAZ za linije 16, 75, 83... u smeru ka Zelenom vencu Krajnje ULAZNO-IZLAZNO stajalište Trg Republike za linije 43, 96, 32E... SMER TRG REPUBLIKE - UŠĆE
PROPISNIK O KALENDARU NATJECANJA
 PRAVILNIK O KALENDARU NATJECANJA HRVATSKOG SPORTSKOG PLESNOG SAVEZA U Zagrebu 18.01.2018 godine. SADRŽAJ I. OPĆE ODREDBE... 2 II. UPIS SPORTSKIH PLESNIH NATJECANJA U KALENDAR NATJECANJA... 3 III. PRIJAVE
PRAVILNIK O KALENDARU NATJECANJA HRVATSKOG SPORTSKOG PLESNOG SAVEZA U Zagrebu 18.01.2018 godine. SADRŽAJ I. OPĆE ODREDBE... 2 II. UPIS SPORTSKIH PLESNIH NATJECANJA U KALENDAR NATJECANJA... 3 III. PRIJAVE
CIJELI BROJEVI 1.) Kako još nazivamo pozitivne cijele brojeve? 1.) Za što je oznaka? 2.) Ispiši skup prirodnih brojeva! 3.) Kako označavamo skup priro
 CIJELI BROJEVI 1.) Kako još nazivamo pozitivne cijele brojeve? 1.) Za što je oznaka? 2.) Ispiši skup prirodnih brojeva! 3.) Kako označavamo skup prirodnih brojeva? 4.) Pripada li 0 skupu prirodnih brojeva?
CIJELI BROJEVI 1.) Kako još nazivamo pozitivne cijele brojeve? 1.) Za što je oznaka? 2.) Ispiši skup prirodnih brojeva! 3.) Kako označavamo skup prirodnih brojeva? 4.) Pripada li 0 skupu prirodnih brojeva?
KORELISANOST REZULTATA MERENJA
 Grđevsk fkultet Osek geoeju geoformtku PROSTIRANJE SLUČAJNIH GREŠAKA U MODELIMA MERENJA Teorj grešk geoetsk merej Verj 00409 Prof r Brko Božć, plgeož SADRŽAJ ZAKONI PRENOSA GREŠAKA MERENJA grešk fukcje
Grđevsk fkultet Osek geoeju geoformtku PROSTIRANJE SLUČAJNIH GREŠAKA U MODELIMA MERENJA Teorj grešk geoetsk merej Verj 00409 Prof r Brko Božć, plgeož SADRŽAJ ZAKONI PRENOSA GREŠAKA MERENJA grešk fukcje
My_P_Red_Bin_Zbir_Free
 БИНОМНА ФОРМУЛА Шт треба знати пре почетка решавања задатака? I Треба знати биному формулу која даје одговор на питање чему је једнак развој једног бинома када га степенујемо са бројем 0 ( ) или ( ) 0!,
БИНОМНА ФОРМУЛА Шт треба знати пре почетка решавања задатака? I Треба знати биному формулу која даје одговор на питање чему је једнак развој једног бинома када га степенујемо са бројем 0 ( ) или ( ) 0!,
Microsoft Word - Svrha projekta.doc
 S V E U Č I L I Š T E U Z A G R E B U FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA Zavod za elektroničke sustave i obradbu informacija FER 2 program, 1. godina diplomskog studija Kolegij: Sustavi za praćenje
S V E U Č I L I Š T E U Z A G R E B U FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA Zavod za elektroničke sustave i obradbu informacija FER 2 program, 1. godina diplomskog studija Kolegij: Sustavi za praćenje
IZBORNO NATJECANJE ZA IMC - RJEŠENJA Zadatak 1. Odredite sve polinome f i g s realnim koeficijentima koji zadovoljavaju jednakost (f(x))
 IZBORNO NATJECANJE ZA IMC - RJEŠENJA 7. 06. 017. Zadata 1. Odredte sve polnome f g s realnm oefcjentma oj zadovoljavaju jednaost (f(x)) 3 (g(x)) = 1, x R. Rješenje. Pretpostavmo da je deg f = n > 0, tada
IZBORNO NATJECANJE ZA IMC - RJEŠENJA 7. 06. 017. Zadata 1. Odredte sve polnome f g s realnm oefcjentma oj zadovoljavaju jednaost (f(x)) 3 (g(x)) = 1, x R. Rješenje. Pretpostavmo da je deg f = n > 0, tada
UDC: : / STRUČNI RAD PRIMENA METODE VIKOR ZA IZBOR STRATEGIJE ODRŽAVANJA THE APPLICATION OF VIKOR METHOD FOR SELECTION OF MAINTEN
 UDC: 620.7:62.79./982.540 STRUČNI RAD PRIMENA METODE VIKOR ZA IZBOR STRATEGIJE ODRŽAVANJA THE APPLICATION OF VIKOR METHOD FOR SELECTION OF MAINTENANCE STRATEGIES Prof. dr Mlan Nkolć, e-mal: mkaczr@sbb.rs
UDC: 620.7:62.79./982.540 STRUČNI RAD PRIMENA METODE VIKOR ZA IZBOR STRATEGIJE ODRŽAVANJA THE APPLICATION OF VIKOR METHOD FOR SELECTION OF MAINTENANCE STRATEGIES Prof. dr Mlan Nkolć, e-mal: mkaczr@sbb.rs
Odreivanje neodreenosti hadronske strukture metodama strojnog ucenja
 Odredivanje neodredenosti hadronske strukture metodama strojnog učenja Ivan Ćorić 1 Mentor: prof. Krešimir Kumerički 1 1 Prirodoslovno matematički fakultet, Fizički odsjek Sveučilište u Zagrebu 29. siječnja
Odredivanje neodredenosti hadronske strukture metodama strojnog učenja Ivan Ćorić 1 Mentor: prof. Krešimir Kumerički 1 1 Prirodoslovno matematički fakultet, Fizički odsjek Sveučilište u Zagrebu 29. siječnja
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br Autonomno kretanje virtualnih objekata Marin Hrkec Zagreb, lipanj 201
 SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br. 6404 Autonomno kretanje virtualnih objekata Marin Hrkec Zagreb, lipanj 2019. iii SADRŽAJ 1. Uvod 1 2. Korišteni alati i tehnologije
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br. 6404 Autonomno kretanje virtualnih objekata Marin Hrkec Zagreb, lipanj 2019. iii SADRŽAJ 1. Uvod 1 2. Korišteni alati i tehnologije
MAT-KOL (Banja Luka) XXIV (3)(2018), DOI: /МК A ISSN (o) ISSN (o) ZAŠTO K
 AT-KOL (Banja Luka) XXIV ()(018) 147-151 http://wwwmvblrg/dmbl/dmblhtm DOI: 10751/МК180147A ISSN 054-6969 () ISSN 1986-588 () ZAŠTO KOPLIKOVANO KADA OŢE JEDNOSTAVNO Dr Šefket Arslanagć Sarajev 1 Saţetak
AT-KOL (Banja Luka) XXIV ()(018) 147-151 http://wwwmvblrg/dmbl/dmblhtm DOI: 10751/МК180147A ISSN 054-6969 () ISSN 1986-588 () ZAŠTO KOPLIKOVANO KADA OŢE JEDNOSTAVNO Dr Šefket Arslanagć Sarajev 1 Saţetak
Ukupno bodova:
 Agencija za odgoj i obrazovanje Hrvatska zajednica tehničke kulture 56. ŽUPANIJSKO NATJECANJE MLADIH TEHNIČARA 204. PISANA PROVJERA ZNANJA 8. RAZRED Zaporka učenika: ukupan zbroj bodova pisanog uratka
Agencija za odgoj i obrazovanje Hrvatska zajednica tehničke kulture 56. ŽUPANIJSKO NATJECANJE MLADIH TEHNIČARA 204. PISANA PROVJERA ZNANJA 8. RAZRED Zaporka učenika: ukupan zbroj bodova pisanog uratka
Microsoft Word - Vezba 3_Stilometrija-uputstvo za vezbu (Repaired).doc
 СПЕКТРОСКОПСКО ОДРЕЂИВАЊЕ САСТАВА ЛЕГУРЕ Табела 1: Области таласних дужина у видљивом делу спектра за сваку боју појединачно Боја Област таласних дужина nm Љубичаста 400 420 Индиго 420 440 Плава 440 490
СПЕКТРОСКОПСКО ОДРЕЂИВАЊЕ САСТАВА ЛЕГУРЕ Табела 1: Области таласних дужина у видљивом делу спектра за сваку боју појединачно Боја Област таласних дужина nm Љубичаста 400 420 Индиго 420 440 Плава 440 490
Microsoft Word - 13-Mreze.doc
 MREŽE RAČUNALA Mreža (engl. network) skup (sustav) povezanih računala i njihovih perifernih uređaja koji omogućava brzu razmjenu podataka među njima neovisno o njihovoj udaljenosti te zajedničku upotrebu
MREŽE RAČUNALA Mreža (engl. network) skup (sustav) povezanih računala i njihovih perifernih uređaja koji omogućava brzu razmjenu podataka među njima neovisno o njihovoj udaljenosti te zajedničku upotrebu
oae_10_dom
 ETF U BEOGRADU, ODSEK ZA ELEKTRONIKU Milan Prokin Radivoje Đurić domaći zadaci - 2010 1. Domaći zadatak 1.1. a) [4] Nacrtati direktno spregnut pojačavač (bez upotrebe sprežnih kondenzatora) sa NPN tranzistorima
ETF U BEOGRADU, ODSEK ZA ELEKTRONIKU Milan Prokin Radivoje Đurić domaći zadaci - 2010 1. Domaći zadatak 1.1. a) [4] Nacrtati direktno spregnut pojačavač (bez upotrebe sprežnih kondenzatora) sa NPN tranzistorima
SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE ZAVRŠNI RAD Mario Svačina Zagreb, 2014.
 SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE ZAVRŠNI RAD Mario Svačina Zagreb, 2014. SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE ZAVRŠNI RAD Mentor: Prof. dr. sc. Dubravko Majetić
SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE ZAVRŠNI RAD Mario Svačina Zagreb, 2014. SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE ZAVRŠNI RAD Mentor: Prof. dr. sc. Dubravko Majetić
Рачунарска интелигенција
 Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Microsoft Word - ETF Journal - Maja
 PERFORMANSE DUAL-DIVERSITY SISTEMA U USLOVIMA KORELISANIH I NEIDENTIČNIH FEDINGA U GRANAMA Maja Ilć-Delbašć, Mlca Pejanovć-Đuršć Ključne rječ: korelacja,ber, dversty Sažetak: U radu su analzrane BER (Bt
PERFORMANSE DUAL-DIVERSITY SISTEMA U USLOVIMA KORELISANIH I NEIDENTIČNIH FEDINGA U GRANAMA Maja Ilć-Delbašć, Mlca Pejanovć-Đuršć Ključne rječ: korelacja,ber, dversty Sažetak: U radu su analzrane BER (Bt
Konacne grupe, dizajni i kodovi
 Konačne grupe, dizajni i kodovi Andrea Švob (asvob@math.uniri.hr) 1. veljače 2011. Andrea Švob (asvob@math.uniri.hr) () Konačne grupe, dizajni i kodovi 1. veljače 2011. 1 / 36 J. Moori, Finite Groups,
Konačne grupe, dizajni i kodovi Andrea Švob (asvob@math.uniri.hr) 1. veljače 2011. Andrea Švob (asvob@math.uniri.hr) () Konačne grupe, dizajni i kodovi 1. veljače 2011. 1 / 36 J. Moori, Finite Groups,
OpenDNS Family Shield CERT.hr-PUBDOC
 OpenDNS Family Shield CERT.hr-PUBDOC-2019-6-381 Sadržaj 1 UVOD... 3 2 INSTALACIJA USLUGE OPENDNS FAMILY SHIELD... 5 2.1 KONFIGURACIJA NA OPERACIJSKOM SUSTAVU WINDOWS 10... 5 2.2 KONFIGURACIJA NA KUĆNOM/UREDSKOM
OpenDNS Family Shield CERT.hr-PUBDOC-2019-6-381 Sadržaj 1 UVOD... 3 2 INSTALACIJA USLUGE OPENDNS FAMILY SHIELD... 5 2.1 KONFIGURACIJA NA OPERACIJSKOM SUSTAVU WINDOWS 10... 5 2.2 KONFIGURACIJA NA KUĆNOM/UREDSKOM
ALIP1_udzb_2019.indb
 Razmislimo Kako u memoriji računala prikazujemo tekst, brojeve, slike? Gdje se spremaju svi ti podatci? Kako uopće izgleda memorija računala i koji ju elektronički sklopovi čine? Kako biste znali odgovoriti
Razmislimo Kako u memoriji računala prikazujemo tekst, brojeve, slike? Gdje se spremaju svi ti podatci? Kako uopće izgleda memorija računala i koji ju elektronički sklopovi čine? Kako biste znali odgovoriti
JMBAG IME I PREZIME BROJ BODOVA MJERA I INTEGRAL 2. kolokvij 29. lipnja (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni!) 1. (
 MJERA I INTEGRAL. kolokvij 9. lipnja 018. (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni! 1. (ukupno 6 bodova Neka je (, F, µ prostor s mjerom, neka je (f n n1 niz F-izmjerivih funkcija
MJERA I INTEGRAL. kolokvij 9. lipnja 018. (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni! 1. (ukupno 6 bodova Neka je (, F, µ prostor s mjerom, neka je (f n n1 niz F-izmjerivih funkcija
ŠTO ZNAČI ZAHTIJEV ZA KROV ODNOSNO KROVNI POKROV, BROOF (t1), I KAKO SE TO SVOJSTVO ISPITUJE I DOKAZUJE Tomislav Skušić, dipl.ing. Laboratorij za topl
 ŠTO ZNAČI ZAHTIJEV ZA KROV ODNOSNO KROVNI POKROV, BROOF (t1), I KAKO SE TO SVOJSTVO ISPITUJE I DOKAZUJE Tomislav Skušić, dipl.ing. Laboratorij za toplinska mjerenja d.o.o. Laboratorij djeluje u području
ŠTO ZNAČI ZAHTIJEV ZA KROV ODNOSNO KROVNI POKROV, BROOF (t1), I KAKO SE TO SVOJSTVO ISPITUJE I DOKAZUJE Tomislav Skušić, dipl.ing. Laboratorij za toplinska mjerenja d.o.o. Laboratorij djeluje u području
PROJEKTOVANJE I PRIMENA WEB PORTALA Snežana Laketa Osnovna škola Vuk Karadžić, Vlasenica kontakt telefon:
 PROJEKTOVANJE I PRIMENA WEB PORTALA Snežana Laketa Osnovna škola Vuk Karadžić, Vlasenica e-mail: snezalaketa@yahoo.com kontakt telefon: 99387 56 733 307 Sažetak Ovaj rad razmatra korišćenje Web portala
PROJEKTOVANJE I PRIMENA WEB PORTALA Snežana Laketa Osnovna škola Vuk Karadžić, Vlasenica e-mail: snezalaketa@yahoo.com kontakt telefon: 99387 56 733 307 Sažetak Ovaj rad razmatra korišćenje Web portala
Sveučilište J.J. Strossmayera Fizika 2 FERIT Predložak za laboratorijske vježbe Određivanje relativne permitivnosti sredstva Cilj vježbe Određivanje r
 Sveučilište J.J. Strossmayera Fizika 2 Predložak za laboratorijske vježbe Cilj vježbe Određivanje relativne permitivnosti stakla, plastike, papira i zraka mjerenjem kapaciteta pločastog kondenzatora U-I
Sveučilište J.J. Strossmayera Fizika 2 Predložak za laboratorijske vježbe Cilj vježbe Određivanje relativne permitivnosti stakla, plastike, papira i zraka mjerenjem kapaciteta pločastog kondenzatora U-I
Matrice. Algebarske operacije s matricama. - Predavanje I
 Matrice.. Predavanje I Ines Radošević inesr@math.uniri.hr Odjel za matematiku Sveučilišta u Rijeci Matrice... Matrice... Podsjeti se... skup, element skupa,..., matematička logika skupovi brojeva N,...,
Matrice.. Predavanje I Ines Radošević inesr@math.uniri.hr Odjel za matematiku Sveučilišta u Rijeci Matrice... Matrice... Podsjeti se... skup, element skupa,..., matematička logika skupovi brojeva N,...,
PowerPoint Presentation
 Факултет организационих наука Центар за пословно одлучивање Системи за препоруку П8: Системи за препоруку Закључивање на основу случајева Системи за препоруку 2 Закључивање на основу случајева ПРОНАЂЕНО
Факултет организационих наука Центар за пословно одлучивање Системи за препоруку П8: Системи за препоруку Закључивање на основу случајева Системи за препоруку 2 Закључивање на основу случајева ПРОНАЂЕНО
ŽUPANIJSKO NATJECANJE IZ MATEMATIKE 28. veljače razred - rješenja OVDJE SU DANI NEKI NAČINI RJEŠAVANJA ZADATAKA. UKOLIKO UČENIK IMA DRUGAČIJI
 ŽUANIJSKO NATJECANJE IZ MATEMATIKE 8. veljače 09. 8. razred - rješenja OVDJE SU DANI NEKI NAČINI RJEŠAVANJA ZADATAKA. UKOLIKO UČENIK IMA DRUGAČIJI OSTUAK RJEŠAVANJA, ČLAN OVJERENSTVA DUŽAN JE I TAJ OSTUAK
ŽUANIJSKO NATJECANJE IZ MATEMATIKE 8. veljače 09. 8. razred - rješenja OVDJE SU DANI NEKI NAČINI RJEŠAVANJA ZADATAKA. UKOLIKO UČENIK IMA DRUGAČIJI OSTUAK RJEŠAVANJA, ČLAN OVJERENSTVA DUŽAN JE I TAJ OSTUAK
Verovatnoća - kolokvijum 17. decembar Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je
 Verovatnoća - kolokvijum 17. decembar 2016. 1. Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je 0.8. Ako je ispit težak, verovatnoća da se prvo pitanje
Verovatnoća - kolokvijum 17. decembar 2016. 1. Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je 0.8. Ako je ispit težak, verovatnoća da se prvo pitanje
XIII. Hrvatski simpozij o nastavi fizike Istraživački usmjerena nastava fizike na Bungee jumping primjeru temeljena na analizi video snimke Berti Erja
 Istraživački usmjerena nastava fizike na Bungee jumping primjeru temeljena na analizi video snimke Berti Erjavec Institut za fiziku, Zagreb Sažetak. Istraživački usmjerena nastava fizike ima veću učinkovitost
Istraživački usmjerena nastava fizike na Bungee jumping primjeru temeljena na analizi video snimke Berti Erjavec Institut za fiziku, Zagreb Sažetak. Istraživački usmjerena nastava fizike ima veću učinkovitost
Nastavna cjelina: 1. Jezik računala Kataloška tema: 1.1. Bit 1.2. Brojevi zapisani četvorkom bitova Nastavna jedinica: 1.1. Bit 1.2. Brojevi zapisan
 Nastavna cjelina: 1. Osnove IKT-a Kataloška tema: 1.6. Paralelni i slijedni ulazno-izlazni pristupi računala 1.7. Svojstva računala Unutar računala podatci su prikazani električnim digitalnim signalima
Nastavna cjelina: 1. Osnove IKT-a Kataloška tema: 1.6. Paralelni i slijedni ulazno-izlazni pristupi računala 1.7. Svojstva računala Unutar računala podatci su prikazani električnim digitalnim signalima
Microsoft PowerPoint - fakultet - Gajić.ppt [Način kompatibilnosti]
![Microsoft PowerPoint - fakultet - Gajić.ppt [Način kompatibilnosti] Microsoft PowerPoint - fakultet - Gajić.ppt [Način kompatibilnosti]](/thumbs/101/149035780.jpg) PROZORI adekvatna postavka dozvoljene vrijednosti U-koeficijenta Doc. dr Darija Gajić, dipl. ing. arh. Arhitektonsko-građevinsko-geodetski fakultet Univerziteta u Banjoj Luci ENERGETSKI INTENZITET PPE/BDP
PROZORI adekvatna postavka dozvoljene vrijednosti U-koeficijenta Doc. dr Darija Gajić, dipl. ing. arh. Arhitektonsko-građevinsko-geodetski fakultet Univerziteta u Banjoj Luci ENERGETSKI INTENZITET PPE/BDP
CRNOGORSKI KOMITET MEĐUNARODNOG VIJEĆA
 CRNOGORSKI KOMITET CIGRE Senda Grboć, dpl.el.ng JU Sredna elektro-ekonomska škola, Belo ole senda_grboc@hotmal.com prof. Emertus dr Ila Vuošeć, dpl.el.ng Elektrotehnčk fakultet, odgorca la@ac.me prof.dr
CRNOGORSKI KOMITET CIGRE Senda Grboć, dpl.el.ng JU Sredna elektro-ekonomska škola, Belo ole senda_grboc@hotmal.com prof. Emertus dr Ila Vuošeć, dpl.el.ng Elektrotehnčk fakultet, odgorca la@ac.me prof.dr
Algoritmi SŠ P1
 Državno natjecanje iz informatike Srednja škola Prvi dan natjecanja 2. ožujka 219. ime zadatka BADMINTON SJEME MANIPULATOR vremensko ograničenje 1 sekunda 1 sekunda 3 sekunde memorijsko ograničenje 512
Državno natjecanje iz informatike Srednja škola Prvi dan natjecanja 2. ožujka 219. ime zadatka BADMINTON SJEME MANIPULATOR vremensko ograničenje 1 sekunda 1 sekunda 3 sekunde memorijsko ograničenje 512
Državno natjecanje / Osnove informatike Srednje škole Zadaci U sljedećim pitanjima na odgovore odgovaraš upisivanjem slova koji se nalazi ispred
 Zadaci. 8. U sljedećim pitanjima na odgovore odgovaraš upisivanjem slova koji se nalazi ispred točnog odgovora, u za to predviđen prostor. Odgovor Ako želimo stvoriti i pohraniti sliku, ali tako da promjenom
Zadaci. 8. U sljedećim pitanjima na odgovore odgovaraš upisivanjem slova koji se nalazi ispred točnog odgovora, u za to predviđen prostor. Odgovor Ako želimo stvoriti i pohraniti sliku, ali tako da promjenom
U trotjednom istraživanju „Kako mršavimo“ provedenom na portalu Ordinacija
 ISTRAŽIVANJE PORTALA ORDINACIJA.HR: Hrvati pola života provedu na dijeti! Za idealnu liniju spremni smo narušiti svoje zdravlje! U trotjednom istraživanju (kolovoz/rujan 2010.) portala Ordinacija.hr Kako
ISTRAŽIVANJE PORTALA ORDINACIJA.HR: Hrvati pola života provedu na dijeti! Za idealnu liniju spremni smo narušiti svoje zdravlje! U trotjednom istraživanju (kolovoz/rujan 2010.) portala Ordinacija.hr Kako
Planovi prijema za numeričke karakteristike kvaliteta
 U N I V E Z I T E T U B E O G A D U F A K U L T E T O G A N I Z A C I O N I H N A U K A Kontrola valteta (osnovne aademse studje) Stablnost procesa numerče ontrolne arte 1. U određenm vremensm ntervalma
U N I V E Z I T E T U B E O G A D U F A K U L T E T O G A N I Z A C I O N I H N A U K A Kontrola valteta (osnovne aademse studje) Stablnost procesa numerče ontrolne arte 1. U određenm vremensm ntervalma
Microsoft PowerPoint - 18 Rapid prototyping.ppt
 Rapid Prototyping doc.dr. Samir Lemeš Rapid Prototyping Osnovni pojmovi i upotreba Fused Deposition Modeling Selektivno lasersko sinterovanje Laminated Object Manufacturing Laser Engineered
Rapid Prototyping doc.dr. Samir Lemeš Rapid Prototyping Osnovni pojmovi i upotreba Fused Deposition Modeling Selektivno lasersko sinterovanje Laminated Object Manufacturing Laser Engineered
LAB PRAKTIKUM OR1 _ETR_
 UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA, TELEKOMUNIKACIJE I RAČUNARI PREDMET: OSNOVE RAČUNARSTVA 1 FOND ČASOVA: 2+1+1 LABORATORIJSKA VJEŽBA BROJ 1 NAZIV: REALIZACIJA
UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA, TELEKOMUNIKACIJE I RAČUNARI PREDMET: OSNOVE RAČUNARSTVA 1 FOND ČASOVA: 2+1+1 LABORATORIJSKA VJEŽBA BROJ 1 NAZIV: REALIZACIJA
Microsoft Word - 24ms241
 Zadatak (Branko, srednja škola) Parabola zadana jednadžbom = p x prolazi točkom tangente na tu parabolu u točki A? A,. A. x + = 0 B. x 8 = 0 C. x = 0 D. x + + = 0 Rješenje b a b a b a =, =. c c b a Kako
Zadatak (Branko, srednja škola) Parabola zadana jednadžbom = p x prolazi točkom tangente na tu parabolu u točki A? A,. A. x + = 0 B. x 8 = 0 C. x = 0 D. x + + = 0 Rješenje b a b a b a =, =. c c b a Kako
Slide 1
 Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
Prof. dr. sc. Aleksandra Čižmešija, izv. prof., PMF MO, Sveučilište u Zagrebu Prof. dr. sc. Hrvoje Šikić, red. prof., PMF MO, Sveučilište u Zagrebu Pr
 Prof. dr. sc. Aleksandra Čižmešija, izv. prof., PMF MO, Sveučilište u Zagrebu Prof. dr. sc. Hrvoje Šikić, red. prof., PMF MO, Sveučilište u Zagrebu Prof. dr. sc. Neven Elezović, red. prof., FER, Sveučilište
Prof. dr. sc. Aleksandra Čižmešija, izv. prof., PMF MO, Sveučilište u Zagrebu Prof. dr. sc. Hrvoje Šikić, red. prof., PMF MO, Sveučilište u Zagrebu Prof. dr. sc. Neven Elezović, red. prof., FER, Sveučilište
Kriteriji ocjenjivanja 6razred
 Kriteriji ocjenjivanja 6razred Nastavne cjeline: 1. Obrada teksta 2. Računalne mreže 3. Internet 4. Multimediji 5. Izrada prezentacija 12 Nastavna cjelina: OBRADA TEKSTA Dobar (3) Dovoljan (2). prepoznaje
Kriteriji ocjenjivanja 6razred Nastavne cjeline: 1. Obrada teksta 2. Računalne mreže 3. Internet 4. Multimediji 5. Izrada prezentacija 12 Nastavna cjelina: OBRADA TEKSTA Dobar (3) Dovoljan (2). prepoznaje
CJENIK STOLCI - HR (Kn).xlsx
 Uredski i konferencijski stolci Tapeciranje u tkaninu po izboru Za plaćanje po predračunu odobravamo DODATN POPUST. Omogućujemo oblik financiranja putem operativnog najma na period od 12-60 mjeseci. DOSTAVA
Uredski i konferencijski stolci Tapeciranje u tkaninu po izboru Za plaćanje po predračunu odobravamo DODATN POPUST. Omogućujemo oblik financiranja putem operativnog najma na period od 12-60 mjeseci. DOSTAVA
ЗБИРКА АЛАТКИ за планирање индивидуализованог образовања Изабране алатке из Водич кроз ресурсе за наставнике Британска ( Колумбија, 2009) Садржај Прил
 ЗБИРКА АЛАТКИ за планрање ндвдуалзованог образовања Изабране алатке з Водч кроз ресурсе за наставнке Бртанска ( Колумбја, 2009) Садржај Прлог 2 : Алатке за сарадњу са родтељма 2А: Псмо родтељма Опс процеса
ЗБИРКА АЛАТКИ за планрање ндвдуалзованог образовања Изабране алатке з Водч кроз ресурсе за наставнке Бртанска ( Колумбја, 2009) Садржај Прлог 2 : Алатке за сарадњу са родтељма 2А: Псмо родтељма Опс процеса
Uvod u računarstvo 2+2
 Programiranje 2 doc.dr.sc. Goranka Nogo PMF Matematički odsjek, Zagreb Kontakt ured: 228, drugi kat e-mail: nogo@math.hr konzultacije: četvrtak, 12:00-14:00 petak, 11:00-12:00 neki drugi termin, uz prethodni
Programiranje 2 doc.dr.sc. Goranka Nogo PMF Matematički odsjek, Zagreb Kontakt ured: 228, drugi kat e-mail: nogo@math.hr konzultacije: četvrtak, 12:00-14:00 petak, 11:00-12:00 neki drugi termin, uz prethodni
Microsoft Word - Kruno Kantoci-NDU.doc
 Zavod za robotku automatzacju prozvodnh sustava Katedra za strojarsku automatku Semnarsk rad z kolegja NEZRAZTO DGTALNO UPRAVLJANJE Snteza P regulatora estmatora varjabl stanja elektromotornog pogona s
Zavod za robotku automatzacju prozvodnh sustava Katedra za strojarsku automatku Semnarsk rad z kolegja NEZRAZTO DGTALNO UPRAVLJANJE Snteza P regulatora estmatora varjabl stanja elektromotornog pogona s
ANALIZA RAČUNOVODSTVENIH POLITIKA PRIZNAVANJA I PROCJENJIVANJA KRATKOTRAJNE IMOVINE Imovina Kratkotrajna imovina Dugotrajna imovina Imovin
 ANALIZA RAČUNOVODSTVENIH POLITIKA PRIZNAVANJA I PROCJENJIVANJA KRATKOTRAJNE IMOVINE Imovina Kratkotrajna imovina Dugotrajna imovina Imovina za koju se očekuje da će biti prodana ili upotrijebljena tijekom
ANALIZA RAČUNOVODSTVENIH POLITIKA PRIZNAVANJA I PROCJENJIVANJA KRATKOTRAJNE IMOVINE Imovina Kratkotrajna imovina Dugotrajna imovina Imovina za koju se očekuje da će biti prodana ili upotrijebljena tijekom
Microsoft PowerPoint - Teorija kretanja vozila-predavanje 3.1.ppt
 ТЕОРИЈА КРЕТАЊА ВОЗИЛА Предавање. гусенична возила, површински притисак ослањања, гусеница на подлогу ослањања G=mg p p гусеница на подлогу ослањања G=mg средњи стварни p тврда подлога средњи стварни p
ТЕОРИЈА КРЕТАЊА ВОЗИЛА Предавање. гусенична возила, површински притисак ослањања, гусеница на подлогу ослањања G=mg p p гусеница на подлогу ослањања G=mg средњи стварни p тврда подлога средњи стварни p
NAZIV PREDMETA UNUTARNJETRGOVINSKO POSLOVANJE II Kod Godina studija 2. Nositelj/i predmeta dr.sc. Ivana Plazibat, prof. Bodovna vrijednost 6 ECTS v.š.
 NAZIV PREDMETA UNUTARNJETRGOVINSKO POSLOVANJE II Kod Godina studija 2. Nositelj/i predmeta dr.sc. Ivana Plazibat, prof. Bodovna vrijednost 6 ECTS v.š. (ECTS) Suradnici nema Način izvođenja nastave P S
NAZIV PREDMETA UNUTARNJETRGOVINSKO POSLOVANJE II Kod Godina studija 2. Nositelj/i predmeta dr.sc. Ivana Plazibat, prof. Bodovna vrijednost 6 ECTS v.š. (ECTS) Suradnici nema Način izvođenja nastave P S
(Microsoft PowerPoint - U\310INKOVITA PREVENCIJA OVISNOSTI-josip_jankovic.pptx)
 Putovi učinkovitog suočavanja s pojavom zloporabe psihoaktivnih supstanci djece i mladih Josip Janković OSNOVNE POSTAVKE Ovisnosti su segment pojave poremećaja u ponašanju a ne posebna kategorija! Suočavanje
Putovi učinkovitog suočavanja s pojavom zloporabe psihoaktivnih supstanci djece i mladih Josip Janković OSNOVNE POSTAVKE Ovisnosti su segment pojave poremećaja u ponašanju a ne posebna kategorija! Suočavanje
Drugi kolokvij iz predmeta Operacijski sustavi 2. srpnja Napomene: PISATI ČITKO! Zadatke 7-10 rješavati na ovom papiru ili uz njih napisati "na
 Drugi kolokvij iz predmeta Operacijski sustavi 2. srpnja 2019. Napomene: PISATI ČITKO! Zadatke 7-10 rješavati na ovom papiru ili uz njih napisati "na papirima". 1. (2) Opisati pristupni sklop za izravni
Drugi kolokvij iz predmeta Operacijski sustavi 2. srpnja 2019. Napomene: PISATI ČITKO! Zadatke 7-10 rješavati na ovom papiru ili uz njih napisati "na papirima". 1. (2) Opisati pristupni sklop za izravni
ULOGA KONTROLE KVALITETE U STVARANJU INFRASTRUKTURE PROSTORNIH PODATAKA Vladimir Baričević, dipl.ing.geod. Dragan Divjak, dipl.ing.geod.
 ULOGA KONTROLE KVALITETE U STVARANJU INFRASTRUKTURE PROSTORNIH PODATAKA Vladimir Baričević, dipl.ing.geod. Dragan Divjak, dipl.ing.geod. Sadržaj NIPP STANDARDI KONCEPT KONTROLE KVALITETE PROCES KONTROLE
ULOGA KONTROLE KVALITETE U STVARANJU INFRASTRUKTURE PROSTORNIH PODATAKA Vladimir Baričević, dipl.ing.geod. Dragan Divjak, dipl.ing.geod. Sadržaj NIPP STANDARDI KONCEPT KONTROLE KVALITETE PROCES KONTROLE
+ Usluge kućne njege za osobe mlađe od 65 godina kroatiska + 1. Opći dojam o službi kućne njege Iznimno sam nezadovoljan/na Prilično sam nezadovoljan/
 Usluge kućne njege za osobe mlađe od 65 godina kroatiska 1. Opći dojam o službi kućne njege Iznimno sam Prilično sam Ni zadovoljan/na niti Prilično sam zadovoljan/na Veoma sam zadovoljan/na a. Koliko ste
Usluge kućne njege za osobe mlađe od 65 godina kroatiska 1. Opći dojam o službi kućne njege Iznimno sam Prilično sam Ni zadovoljan/na niti Prilično sam zadovoljan/na Veoma sam zadovoljan/na a. Koliko ste
knjiga.dvi
 1. Vjerojatnost 1. lgebra dogadaja......................... 1 2. Vjerojatnost............................. 9 3. Klasični vjerojatnosni prostor................. 14 4. eskonačni vjerojatnosni prostor...............
1. Vjerojatnost 1. lgebra dogadaja......................... 1 2. Vjerojatnost............................. 9 3. Klasični vjerojatnosni prostor................. 14 4. eskonačni vjerojatnosni prostor...............
Microsoft PowerPoint - Prvi tjedan [Compatibility Mode]
![Microsoft PowerPoint - Prvi tjedan [Compatibility Mode] Microsoft PowerPoint - Prvi tjedan [Compatibility Mode]](/thumbs/99/139589070.jpg) REAKTORI I BIOREAKTORI PODJELA I OSNOVNI TIPOVI KEMIJSKIH REAKTORA Vanja Kosar, izv. prof. KEMIJSKI REAKTOR I KEMIJSKO RAKCIJSKO INŽENJERSTVO PODJELA REAKTORA I OPĆE BILANCE TVARI i TOPLINE 2 Kemijski
REAKTORI I BIOREAKTORI PODJELA I OSNOVNI TIPOVI KEMIJSKIH REAKTORA Vanja Kosar, izv. prof. KEMIJSKI REAKTOR I KEMIJSKO RAKCIJSKO INŽENJERSTVO PODJELA REAKTORA I OPĆE BILANCE TVARI i TOPLINE 2 Kemijski
STONEX S5 GNSS prijemnik GNSS prijemnik visoke točnosti za prikupljanje podataka za GIS
 STOX S5 GSS prijemnik GSS prijemnik visoke točnosti za prikupljanje podataka za GIS STOX S5 GSS prijemnik rezultat je višegodišnjeg razvoja i iskustva u izradi svestranih prijemnika. Zahvaljujući njegovoj
STOX S5 GSS prijemnik GSS prijemnik visoke točnosti za prikupljanje podataka za GIS STOX S5 GSS prijemnik rezultat je višegodišnjeg razvoja i iskustva u izradi svestranih prijemnika. Zahvaljujući njegovoj
Programski jezici i strukture podataka 2018/2019. Programski jezici i strukture podataka Računarske vežbe vežba 10 Zimski semestar 2018/2019. Studijsk
 Programski jezici i strukture podataka Računarske vežbe vežba 10 Zimski semestar 2018/2019. Studijski program: Informacioni inženjering Informacioni inženjering 1 Rekurzivne funkcije Binarna stabla Informacioni
Programski jezici i strukture podataka Računarske vežbe vežba 10 Zimski semestar 2018/2019. Studijski program: Informacioni inženjering Informacioni inženjering 1 Rekurzivne funkcije Binarna stabla Informacioni
Microsoft Word - VEROVATNOCA II deo.doc
 VEROVATNOĆA - ZADAI (II DEO) Klasična definicija verovatnoće Verovatnoća dogañaja A jednaka je količniku broja povoljnih slučajeva za dogañaj A i broja svih mogućih slučajeva. = m n n je broj svih mogućih
VEROVATNOĆA - ZADAI (II DEO) Klasična definicija verovatnoće Verovatnoća dogañaja A jednaka je količniku broja povoljnih slučajeva za dogañaj A i broja svih mogućih slučajeva. = m n n je broj svih mogućih
Istraživanje turističkog tržišta
 ISTRAŽIVANJE TURISTIČKOG TRŽIŠTA asistent:branislava Hristov Stančić branislava@ekof.bg.ac.rs Suština i sadržaj istraživanja tržišta Istraživanje tržišta istraživanje marketinga Istraživanje marketinga
ISTRAŽIVANJE TURISTIČKOG TRŽIŠTA asistent:branislava Hristov Stančić branislava@ekof.bg.ac.rs Suština i sadržaj istraživanja tržišta Istraživanje tržišta istraživanje marketinga Istraživanje marketinga
Univerzitet u Beogradu Elektrotehnički fakultet Katedra za energetske pretvarače i pogone ISPIT IZ SINHRONIH MAŠINA (13E013SIM) 1. Poznati su podaci o
 Univerzitet u Beogradu Elektrotehnički akultet Katedra za energetske pretvarače i pogone ISPIT IZ SINHRONIH MAŠINA (13E013SIM) 1. Poznati su podaci o namotaju statora sinhronog motora sa stalnim magnetima
Univerzitet u Beogradu Elektrotehnički akultet Katedra za energetske pretvarače i pogone ISPIT IZ SINHRONIH MAŠINA (13E013SIM) 1. Poznati su podaci o namotaju statora sinhronog motora sa stalnim magnetima
χ2 test
 χ es uporebljava se kada želimo uvrdii odsupaju li dobivene - opažene rekvencije ( o ) od eoreskih ili očekivanih rekvencija uz određene hipoeze ( ). χ es o spada u neparamerijsku saisiku, primjenjiv i
χ es uporebljava se kada želimo uvrdii odsupaju li dobivene - opažene rekvencije ( o ) od eoreskih ili očekivanih rekvencija uz određene hipoeze ( ). χ es o spada u neparamerijsku saisiku, primjenjiv i
Microsoft Word - 4.Ee1.AC-DC_pretvaraci.10
 AC-DC ПРЕТВАРАЧИ (ИСПРАВЉАЧИ) Задатак 1. Једнофазни исправљач са повратном диодом, са слике 1, прикључен на напон 1 V, 5 Hz напаја потрошач велике индуктивности струјом од 1 А. Нацртати таласне облике
AC-DC ПРЕТВАРАЧИ (ИСПРАВЉАЧИ) Задатак 1. Једнофазни исправљач са повратном диодом, са слике 1, прикључен на напон 1 V, 5 Hz напаја потрошач велике индуктивности струјом од 1 А. Нацртати таласне облике
ANALIZE MASENOM SPEKTROMETRIJOM SEKUNDARNIH MOLEKULARNIH IONA ZA PRIMJENE U FORENZICI
 ANALIZE MASENOM SPEKTROMETRIJOM SEKUNDARNIH MOLEKULARNIH IONA ZA PRIMJENE U FORENZICI Marko Crnac Fizički odsjek, PMF Mentor: dr. sc. Iva Bogdanović Radović Laboratorij za interakcije ionskih snopova Institut
ANALIZE MASENOM SPEKTROMETRIJOM SEKUNDARNIH MOLEKULARNIH IONA ZA PRIMJENE U FORENZICI Marko Crnac Fizički odsjek, PMF Mentor: dr. sc. Iva Bogdanović Radović Laboratorij za interakcije ionskih snopova Institut
Microsoft Word - 01-NASLOVNA.doc
 I. polavle UVOD 1. OPĆENITO 1.1. Mehana čvrsto deformablno tela Teora elastčnost plastčnost e dscplna oa prpada znanost o čvrstom deformablnom telu, al e sto tao do mehane ontnuuma u onom delu o se odnos
I. polavle UVOD 1. OPĆENITO 1.1. Mehana čvrsto deformablno tela Teora elastčnost plastčnost e dscplna oa prpada znanost o čvrstom deformablnom telu, al e sto tao do mehane ontnuuma u onom delu o se odnos
Microsoft Word - PusenjeNaRadnomMjestu.doc
 Zagreb, prosinac 2008. Sadržaj 1. Uvod... 1 2. Struktura ispitanika istraživanja... 1 3. Struktura (ne)pušača... 2 4.... 4 4.1...4 4.2...8 5. Novi zakon o zabrani pušenja... 9 Popis grafikona Grafikon
Zagreb, prosinac 2008. Sadržaj 1. Uvod... 1 2. Struktura ispitanika istraživanja... 1 3. Struktura (ne)pušača... 2 4.... 4 4.1...4 4.2...8 5. Novi zakon o zabrani pušenja... 9 Popis grafikona Grafikon
