Klaster analiza
|
|
|
- Милан Радовић
- пре 5 година
- Прикази:
Транскрипт
1 Klaster analiza Nenad Mitić Matematički fakultet
2 Šta je klaster analiza? Pronalaženje grupa objekata takvih da su objekti u grupi medjusobno slični (ili povezani), i da su objekti u različitim grupama medjusobno različiti (ili nepovezani) snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.2
3 Šta nije klaster analiza? snovani na Klasifikacija pod nadzorom Jednostavna podela (npr. podela studenata po prvom slovu prezimena) Rezultat upita Podela grafa sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.3
4 Dvosmislenost pojma snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.4
5 Tipovi Klasterovanje je postupak dobijanja Particiono - podela skupa u nepreklapajuće podskupove (klastere) takve da je svaki podatak tačno u jednom podskupu Hijerarhijsko - skup ugnježdenih organizovan u obliku hijerarhijskog drveta snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.5
6 Particiono snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.6
7 Hijerarhijsko snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.7
8 Tipovi Eksluzivno/neeksluzivno. U neeksluzivnom klasterovanju tačke mogu da se nalaze u više. Mogu da predstavljaju više klasa ili graničnih tačaka Rasplinuto/nerasplinuto. U rasplinutom klasterovanju tačka pripada svakom klasteru sa nekom težinom izmedju 0 i 1 (zbir svih težina je jednak 1) Delimično/kompletno (klasteruje se samo deo ) Heterogeno/homogeno (klasteri različite veličine, oblika i gustine) snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.8
9 Tipovi Dobro razdvojeni klasteri (eng. well-separated) snovani na Klaster je skup tačaka takvih da je bilo koja tačka u klasteru bliže (ili više slična) ostalim tačkama u klasteru nego tačkama koje nisu u klasteru Klasteri zasnovani na centru (eng. center-based, prototype-based) sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi Klaster je skup objekata takvih da je bilo koji objekat u klasteru bliže (ili više sličan) prototipu ( centru ) u odnosu na prototipove (centre) ostalih. Centar je često centroid (prosek svih tačaka u klasteru) ili medoid (najreprezentativnija tačka u klasteru) 6.9
10 Tipovi (nastavak) Klasteri zasnovani na susedstvu (eng. contiguous) snovani na Klaster je skup tačaka takvih da je tačka u klasteru bliža (ili više slična) jednoj ili više tačaka u klasteru nego bilo kojoj tački koja nije u klasteru Klasteri zasnovani na gustini (eng. density-based) sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi Klasteri su oblasti sa velikom gustinom tačaka koje su razdvojene oblastima sa malom gustinom tačaka. Koriste se kada su klasteri nepravilni ili isprepleteni, i kada je prisutan šum ili elementi van granica 6.10
11 Tipovi (nastavak) snovani na Klasteri zasnovani na grafovima Konceptualni klasteri/ na osnovu zajedničkih osobina (eng. conceptual) sakupljajućeg razdvajajućeg snovani na Opisani ciljnom funkcijom (eng. described by an objective function) Spoljašnji kriterijumi 6.11
12 Cilj: uklanjanje elemenata van granica Modeli sa filtriranjem: svakoj karakteristici se dodeli odredjena vrednost koja predstavlja granicu za isključivanje Modeli sa omotačem: algoritam za se koristi da bi se odredila važnost skupa karakteristika Neke karakteristike : tip podatka, dimenzionalnost, tip atributa, tip raspodele, raštrkasnost, gustina,... snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.12
13 Vrste algoritama za zasnovani na (prototipovima) hijerarhijskog zasnovani na zasnovani na verovatnosnim modelima zasnovani na grafovima snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.13
14 snovani na Osnovni princip: uzima se k reprezentativnih predstavnika Y 1, Y 2,... Y k, gde je k broj traženih i računa rastojanje tačaka X 1, X 2,..., X n do njih. Cilj je tako odrediti reprezentativne predstavnike koji minimizuju funkciju snovani na sakupljajućeg razdvajajućeg O = n [min j Dist(X i, Y j )] i=1 snovani na Funkcije rastojanja i reprezentativni predstavnici mogu da se biraju na različite načine. Spoljašnji kriterijumi 6.14
15 snovani na podacima snovani na /* Skup : D, Broj reprezent. : k */ _sa (D, k) begin inicijalni izbor skupa reprezentativnih predstavnika S; repeat Formiraj klastere (C1,...Ck) dodelom svake tacke iz D najblizem predstavniku iz S koristeci funkciju rastojanja Dist(x,x); Ponovo formiraj S odredjivanjem novog predstavnika Yj za svaki Cj koji minimizuje prethodnu funkciju O until doslo je do konvergencije; return (C1,..., Ck); end sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.15
16 Pristup particionim m, model sa prototipom Svakom klasteru je pridružen centroid (centralna tačka) K broj koji mora da se navede Svaka tačka je dodeljena klasteru sa najbližim centroidom. Na primer, pripadnost klasteru se odredjuje pomoću zbira kvadarata Euklidskog rastojanja (kosinusnog rastojanja,...) do najbližeg reprezentativnih predstavnika Dist(X, Y ) = X i Y 2 snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.16
17 : primer snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.17
18 : primer snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.18
19 : primer snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.19
20 : primer snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.20
21 : primer snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.21
22 : primer snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.22
23 : primer snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.23
24 snovani na Različite mere rastojanja. Varijacija algoritma k-sredina je odredjivanje lokalnog Mahalanobisovog rastojanja Početni centroid se često bira na slučajan način Klasteri mogu da se razlikuju - loši rezultati!! Uobičajeno je da je centroid srednja vrednost tačaka u klasteru sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.24
25 snovani na Algoritam konvergira za pomenute mere. Najveći deo konvergencije se dešava u prvih nekoliko iteracija Uslov zaustavljanja - broj tačaka koji promeni klaster Složenost: vremenska O(n K I d), prostorna O((n + K ) d) (n = broj tačaka, K = broj, I = broj iteracija, d = broj atributa) sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.25
26 Evaluacija metode K-sredina Za podatke u Euklidskom prostoru se najčešće se kao mera koristi zbir kvadrata grešaka (eng. sum of squared errors, SSE) Za svaku tačku, greška je rastojanje do najbližeg centroida () Formalno SSE = K i=1 x C i dist(c i, x) 2 gde je x je tačka u klasteru C i i, c i je reprezentativna tačka u klasteru C i i snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.26
27 Evaluacija metode K-sredina Od dva moguća bira se onaj sa manjom SSE Različite mere rastojanja. Varijacija algoritma k-sredina je odredjivanje lokalnog Mahalanobisovog rastojanja Jedan od načina za smanjenje SSE je povećanje broja K Dobro sa malim K može da ima manju SSE grešku od lošeg sa velikim K snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.27
28 Evaluacija metode K-sredina Za dokumente se kao mera koristi kosinusno rastojanje Podaci se predstavljaju preko matrice termova Kohezija - stepen sličnosti dokumentata u klasteru sa centroidom Ukupna kohezija = K i=1 x C i cosinus(c i, x) snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.28
29 snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi Optimalno i suboptimalno 6.29
30 Važnost izbora početnog centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.30
31 Važnost izbora početnog centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.31
32 Važnost izbora početnog centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.32
33 Važnost izbora početnog centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.33
34 Važnost izbora početnog centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.34
35 Važnost izbora početnog centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.35
36 Važnost izbora početnog centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.36
37 Važnost izbora početnog centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.37
38 Važnost izbora početnog centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.38
39 Važnost izbora početnog centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.39
40 Važnost izbora početnog centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.40
41 Važnost izbora početnog centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.41
42 Važnost izbora početnog centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.42
43 Izbor početnih centroida Ako postoji K realnih tada je verovatnoća da se izabere po jedan centroid u svakom od njih relativno mala Ako je K veliko šansa za dobar izbor je mala Ako klasteri imaju istu veličinu n, tada važi P = broj nacina za izbor centroida u svakom klasteru broj nacina za izbor K centroida P = K!nK (Kn) K = K! K K Na primer, za K=10, verovatnoća je 10!/10 1 0= Ponekad se inicijalni centroidi sami poravnaju na pravi redosled, a ponekad ne snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.43
44 Izbor početnih centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.44
45 Izbor početnih centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.45
46 Izbor početnih centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.46
47 Izbor početnih centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.47
48 Izbor početnih centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.48
49 Izbor početnih centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.49
50 Izbor početnih centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.50
51 Izbor početnih centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.51
52 Izbor početnih centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.52
53 Izbor početnih centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.53
54 Izbor početnih centroida Uzastopna izvršavanja Svaki sa npr. slučajno izabranim centroidima Izme du njih se izabere klaster sa najmanjim SSE Nad uzorcima se primeni hijerarhijsko i izaberu početni centroidi Izabere se više od K početnih centroida i bira se izme du njih Potrebno je da obuhvate što širi prostor Postprocesiranje Bisekcija K-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.54
55 Preprocesiranje i postprocesiranje Preprocesiranje Normalizacija Eliminacija elemenata van granica (ne važi za svaku aplikaciju, npr. kompresija) Postprocesiranje Eliminacija malih sa elementima van granica Podela sa visokim SSE Integracija koji su blizu i imaju relativno mali SSE Ovi koraci mogu da se koriste u procesu klasterizacije snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.55
56 Rad sa praznim klasterima Osnovni algoritam može da proizvede praznne klastere snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi Strategije za eliminaciju: zamenjuje se centroid 6.56
57 Algoritam bisekcije K-sredina Varijanta K-sredine koja može da proizvede particiono ili hijerarhijsko Osnovna ideja: za dobijanje K podeli se skup svih tačaka u dva, izabere se jedan od njih za podelu, uz ponavljanje postupka sve dok se ne dobije K Različiti načini podele najveći klaster klaster sa najvećim SSE kriterijum zasnovan i na veličini i na veličini SSE-a Često se dobijeni centroidi koriste za ulaz u osnovni K-sredina algoritam snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.57
58 Algoritam bisekcije K-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.58
59 Algoritam bisekcije K-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.59
60 Algoritam bisekcije K-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.60
61 Algoritam bisekcije K-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.61
62 Algoritam bisekcije K-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.62
63 Algoritam bisekcije K-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.63
64 Algoritam bisekcije K-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.64
65 Algoritam bisekcije K-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.65
66 Algoritam bisekcije K-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.66
67 Algoritam bisekcije K-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.67
68 Najbolje radi sa globularnim podacima Nedostaci: ne funkcioniše za klastere proizvoljnog oblika ne funkcioniše za klastere različitih gustina osetljvost na elemente van granica. Mogu da dovedu do jediničnih ili praznih Rastojanje: Mahalanobis k-sredina prepoznaje klastere različitih gustina Problem: odredjivanje reprezentativnih predstavnika i k broja snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.68
69 Ograničenja algoritma k-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.69
70 Ograničenja algoritma k-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.70
71 Ograničenja algoritma k-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.71
72 Prevazilaženje ograničenja alg. k-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.72
73 Prevazilaženje ograničenja alg. k-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.73
74 Prevazilaženje ograničenja alg. k-sredina snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.74
75 Algoritam kernel k-sredina snovani na Kernel trik: transformacija tako da klaster proizvoljnog oblika u novom okruženju postaje pogodan za korišćenje Euklidskog rastojanja sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.75
76 snovani na Koristi se rastojanje taksi blok, odnosno Menhetn. Pokazuje se da reprezentativni predstavnik medijana po svakoj dimenziji C j. Manja osetljivost na elemente van granica sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.76
77 snovani na Koristi se rastojanje taksi blok, odnosno Menhetn. Razlog - uticaj elemenata van granica na medijanu Ponekad je teško da se izračuna centar za odredjene (složene) tipove sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.77
78 /* Skup : D, Broj reprezent. : k */ _sa (D, k) begin inicijalni izbor skupa reprezentativnih predstavnika S izborom iz D; repeat Formiraj klastere (C1,...Ck) dodelom svake tacke iz D najblizem predstavniku iz S koristeci funkciju rastojanja Dist(x,x); Odrediti par Xi iz D i Yj iz S tako da zamena Yj sa Xi daje najbolje moguce povecanje ciljne funkcije O; Izvrsiti zamenu Xi i Yj samo ako je povecanje pozitivno; until nema poboljsanja vrednosti funkcije; return (C1,..., Ck); end snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.78
79 Formiraju skup ugnježdenih organizovanih u obliku hijerahijskog drveta Vizuelizuju se u obliku dendograma ili dijagrama sa ugnejždenim klasterima snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.79
80 Odozdo/naviše - sakupljajuće (eng. aglomerativno). Odozgo/naniže - razdvajajuće (eng. divisive) U oba slučaja formira se hijerahija Tradicionalni hijerarhijski algoritmi koriste matrice sličnosti ili matrice rastojanja Dele ili spajaju po jedan klaster u jednom koraku Inicijalno se ne navodi broj snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.80
81 sakupljajućeg snovani na U početku je svaka tačka jedan klaster U svakom koraku se sakuplja najbliži par u novi klaster sve dok ne ostane jedan (ili k) Glavna razlika izmedju algoritama ovog tipa je izbor funkcije na osnovu koje se vrši spajanje dva Problem - čuvanje matrice rastojanja sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.81
82 sakupljajućeg snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.82
83 sakupljajućeg snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.83
84 sakupljajućeg /* Podatak: D*/ Sakupljajuce_(D) begin inicijalizacija matrice rastojanja M dimenzije n x n na osnovu D; repeat Uzeti najblizi par i i j koristeci M; Kombinovati klastere i i j; Obrisati redove i kolone i i j iz M i formirati novi red i kolonu u M za novodobijeni klaster; Uneti novi red i kolonu u M; until kriterijum izlaska; return tekuci skup ; end snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.84
85 sakupljajućeg snovani na Odredjivanje rastojanja izmedju dva sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.85
86 sakupljajućeg snovani na Odredjivanje rastojanja izmedju dva sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.86
87 sakupljajućeg Najbolja (najmanja, pojedinačna) veza snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.87
88 sakupljajućeg Pogodnost najbolje veze: može da obradi ne-eliptičke klastere snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.88
89 sakupljajućeg Nedostaci najbolje veze: osetljivost na šum i elemente van granica snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.89
90 sakupljajućeg Najgora (najduža, kompletna) veza snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.90
91 sakupljajućeg Pogodnost najgore veze: otpornost na šum i elemente van granica snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.91
92 sakupljajućeg Nedostatak najgore veze: tendencija razbijanja velikih i naginjanje globularnim klasterima snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.92
93 sakupljajućeg Sličnost : prosek rastojanja parova elemenata iz dva snovani na sakupljajućeg razdvajajućeg snovani na slicnost(x, y) x C i,y C j slicnost(c i, C j ) = m i m j Spoljašnji kriterijumi m i, m j broj elemenata C i, C j 6.93
94 sakupljajućeg Prosek rastojanja parova elemenata iz dva Kompromis izme du pojedinačne i kompletne veze Pogodnost: manje je osetljiva na šum i elemente van granica Nedostaci: naklonost ka globularnim klasterima snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.94
95 sakupljajućeg Sličnost : rastojanje centroida snovani na Ward-ova metoda sličnost - povećanje kvadrata greške pri spajanju dva slično proseku rastojanja parova elemenata ako je mera rastojanja kvadrat greške manje je osetljiva na šum i elemente van granica naklonost ka globularnim klasterima Hijerarhijski analogon K-sredina; može da se korsiti za inicijalizaciju K-sredina sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.95
96 sakupljajućeg Rezultati različitim metodama snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.96
97 sakupljajućeg snovani na Vremenska i prostorna složenost Prostorna O(N 2 ) gde je N broj tačaka (zbog matrice sličnosti) Vremenska O(N 3 ): N koraka u kojima se računaju elemenati mastrice sličnosti (O(N 2 )) Može da se smanji na O(N 2 log(n)) sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.97
98 sakupljajućeg Nedostaci sakupljajućeg hijerarhijskog Posle kombinovanja klasteri ne mogu da se razfvoje Ne postoji globalna funkcija koja se direktno minimizuje U zavisnosti od računanja rastojanja javljaju se osetljivost na šum i elemente van granica teškoće u obradi različitih veličina teškoće u obradi neglobularnih tendencija ka razbijanju velikih snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.98
99 Lance-Williams-ova formula za sličnost Neka je klaster R dobijen spajanjem A i B, i neka je p(.,.) funkcija sličnosti. Sličnost R i Q je jednaka p(r, Q) = α A p(a, Q)+α B p(b, Q)+βp(A, B)+γ p(a, Q) p(b, Q) Sve tehnike sakupljajućeg koje mogu da se predstave Lance-Williams-ovom formulom ne moraju da čuvaju originalne tačke, već je moguće da se matrica sličnosti ažurira kod svakog spajanja. snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.99
100 Lance-Williams-ova formula za sličnost p(r, Q) = α A p(a, Q)+α B p(b, Q)+βp(A, B)+γ p(a, Q) p(b, Q) Metoda α A α B β γ Pojedinačna veza 1/2 1/2 0-1/2 Kompletna veza 1/2 1/2 0 1/2 m Prosek grupe A m B m A +m B m A +m B 0 0 m Centroid A m B m A m B m A +m B m A +m Q m A +m B +m Q m A +m B m B +m Q m A +m B +m Q (m A +m B ) 2 0 m Q m A +m B +m Q 0 Ward-ova metoda gde su m A, m B i m Q brojevi elementara u klasterima A, B i Q snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.100
101 razdvajajućeg Počinje se sa jednim klasterom koji uključuje sve tačke U svakom koraku se klaster deli sve dok se ne dodje do toga da svaki klaster sadrži samo jednu tačku ili dok se ne javi k Za deobu može da posluži bilo koji algoritam (na ravnom skupu ) Algoritam bisekcije k-sredina (podela se uvek vrši na 2 ) snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.101
102 razdvajajućeg snovani na /* Podatak: D, Klasterovanje ravnih : A*/ Sakupljajuce_(D, A) begin inicijalizovati drvo T tako da koren sadrzi D; repeat Izabrati list drveta L u T na osnovu predefinisane strategije; Koristeci algoritam A razdvojiti L na L1,..., Lk; Dodati L1,..., Lk kao decu cvora L u T; until kriterijum izlaska; end sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.102
103 snovani na snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.103
104 snovni na mrežama snovani na /* Podatak: D, Gustina tacaka: t, Gustina mreze: p */ Klasterovanje_mreze(D, p, t) begin Diskretizovati svaku dimenziju podatka D u p vrednosti; Odrediti gustinu celija mreze za gustinu tacaka t; Napraviti grafik u kome su guste celije povezane ako su susedne; Odrediti veze delova grafa return tacke u svakoj povezanoj komponenti kao klaster; end sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.104
105 Za zadatu vrednost Eps i broj t, tacka se klasifikuje kao Tacka jezgra ako se u krugu poluprecnika Eps nalazi bar t drugih tacaka Tacka na granici ako se u krugu poluprecnika Eps nalazi manje od t druhih tacaka, ali se nalazi bar jedna tačka jezgra Šum ako nije niti u jezgru niti na granici. Konstruiše se graf povezivanjem svih tačaka u jezgru Svaka povezana celina predstavlja jedan klaster. snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.105
106 snovani na /* Podatak: D, Poluprecnik: eps, Gustina tacaka: t */ (D, p, t) begin Odrediti jezgro, granicu i sum tacaka iz D za par (Eps, t); Formirati graf u kome su povezane tacke koje pripadaju jezgru ako su medjusobno unutar Eps; Odrediti povezane komponente grafa; Svaku tacku na granici dodeliti povezanoj komponenti sa kojom je najbolje povezana; return tacke svake povezane komponenti kao klaster; end sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.106
107 snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.107
108 snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.108
109 Pogodnost algoritma snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.109
110 Nedostatak algoritma snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.110
111 Odre divanje Eps i k Posmatra se ponašanje rastojanja od tačke do suseda za različito k Za tačke iz istog rastojanje je malo ako k nije veće od veličine Varijacije rastojanja nisu velike ako se gustina znatno ne menja Ako tačke nisu u klasteru (npr. šum) rastojanje je znatno veće Računaju se rastojanja za sve snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.111
112 Težak zadatak u realnom okruženju - nenadgledana klasifikacija Interni (unutrašnji) kriterijum jako zavisi od korišćenog algoritma U opštem slučaju nema spoljašnjeg kriterijuma koji je na raspolaganju za proveru Delimično, moguća je provera preko spoljašnjeg kriterijuma ako postoje sintetički generisani podaci za testiranje postoje oznake klasa snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.112
113 Zbir kvadrata rastojanja do centroida Pogodniji za algoritme sa računanjem rastojanja sa mrežama i gustinom? Kohezija i razdvajanje snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.113
114 (nastavak) Kohezija - zbir rastojanja svih veza u klasteru Razdvajanje - zbir rastojanja izme du elemenata u klasteru i elemenata van Odnos rastojanja u klasteru/van : manja vrednost - bolje Uzorak od r parova tačaka: P pripadaju istom klasteru, Q ostale Prosečna rastojanja u i van U klasteru = Van = (X i,x j ) P (X i,x j ) Q dist(x i, X j )/ P dist(x i, X j )/ Q snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.114
115 (nastavak) Senka koeficijent, eng. Silhouette coefficient AvgDisti in prosečno rastojanje X i do tačaka unutar kome pripapda x i ; AvgDisti out prosečno rastojanje X i do tačaka kome ne pripapda x i ; MinDisti out = min{avgdisti out } Koeficijent senke S i u odnosu na i-ti objekat S i = out MinDisti AvgDisti in max{mindist out i, AvgDist in i } Vrednosti bliske 1 - dobro razdvojeni klasteri; negativne vrednost - mešavina u klasterima Dobra osobina - apsolutna vrednost nosi informaciju o kvalitetu snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.115
116 (nastavak) Verovatnosna mera Model sa pomešanim podacima za procenu kvaliteta pojedinačnog Pretpostavka: centroid mešanih je centroid nadjenih Ostali parametri se računaju koristeći metodu sličnu EM (eng. expectation-maximization) algoritmu Korisno kada se znada klasteri trebaju da imaju specifičan oblik snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.116
117 Spoljašnji kriterijumi snovani na Spoljašnji kriterijum Moguć u slučaju sintetički generisanih Matrica konfuzije Različite mere - najčešće Ginijev indeks sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.117
118 Napredni koncepti snovani na Različite vrste za Kategorički podaci Diskretni podaci Višedimenzioni podaci Massivni (po količini) podaci sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.118
119 Napredni koncepti snovani na Odredjivanje kvaliteta Polunadgledano Interaktivno i vizuelno Meta(?) (eng. ensemble) celinom, bez obzira na pojedinačne vredosti sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.119
120 Klasterovanje kategoričkih Jedan način konverzija u binarne podatke Odredjivanje centroida za kategoričke podatke histogram verovatnoća za svaki atribut centroid - kategorička vrednost koja se javlja u najvećem procentu Računanje sličnosti kategoričkih Različiti algoritmi. Npr. ROCK (RObust Clustering using links) je zasnovan na sakupljajućem pristupu gde se klasteri kombinuju koristeći kriterijum sličnosti. snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.120
121 Klasterovanje kategoričkih K-modalno Za svaki od atributa se odredjuje modalna vrednost (vrednost sa najvećom frekvencijom) Modalna vrednost svakog od atributa se odredjuje nezavisno u odnosu na vrednosti drugih atributa zbog čega odabrana reprezentativna vrednost ( centroid ) ne mora da pripada skupu k-modalno može efektivno da se koristi ako su vrednosti kategoričkih atributa ravnomerno rasporedjene Ako vrednosti kategoričkih atributa nisu ravnomerno rasporedjene vrši se normalizacija deobom frekvencije u klasteru sa frekvencijom u kompletnom skupu K-medoid - reprezentativna tačka je iz materijala snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.121
122 Klasterovanje skalabilnih Kompletni podaci ne mogu da se smeste u memoriju snovani na različitim metodama CLARA (Clustering Large Applications) i CLARANS (Clustering Large Applications on RANdomized Search) su zasnovani na uopštenju pristupa klasterovanju pomoću k-medoida CURE (Clustering Using REpresentatives) je sakupljajući algoritam za hijerarhijsko BIRCH (Balanced Iterative Reducing and Clustering using Hiearchies) predstavlja uopštenje algoritma k-sredina na hijerarhijsku metodu odozgo-naniže snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.122
123 Pogodne za (i za klasifikaciju) Slične KNN Uključuju topografsku organizaciju centroida (neurona) Svaki centroid je odre den parom koordinata Pri radu ažuriraju se tekući centroid i centroidi koji su mu u blizini po topografskoj orijentaciji snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.123
124 snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.124
125 Osnovni algoritam Osnovni algoritam snovani na Inicijalizovati centroide repeat Izabrati sledeci objekat Odrediti najblizi centroid izabranom objektu Azurirati centroid i susedne centroide (centroide koji su u blizini) until Centroidi se ne menjaju /dostignut je prag Dodeliti svaki objekat najblizem centroidu i vratiti centroide i klastere sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.125
126 Osnovni algoritam - koraci Incijalizacija slučajan izbor centroida u intervalu posmatranih vrednosti slučajan izbor tačaka za centroide Izbor objekta ako je broj objekata jako veliki, ne koriste se svi Odre divanje najbližeg centroida metrike rastojanja (euklidsko/kosinusno rastojanje) Ažuriranje centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi Terminiranje 6.126
127 snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.127
128 Ažuriranje centroida Neka su m 1,..., m k centroidi Neka je p(t) tekući objekat u trenutku t i neka je njemu najbliži centroid m j U trenutku t + 1 j-ti centroid se ažurira m j (t + 1) = m j (t) + h j (t)(p(t) m j (t)) h(t) odre duje efekat razlike i obično se bira ili dist(r j,r k ) 2 h j (t) = α(t)e 2σ 2 (t) h j (t) = (Gausova funkcija) { α(t) ako dist(r j, r k ) prag 0 inace gde je 0 < α(t) < 1, r k = (x k, y k ) su koordinate centroida, a dist(r j, r k ) je Euklidsko rastojanje izme du dva centroida snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.128
129 snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.129
130 Prednosti i ograničenja Prednosti Susedni klasteri su više u relaciji od nesusednih Pogodno za vizuelizaciju odre duje strukturu Nedostaci Potreban odabir parametara, funkcije za računaje susedstva i izbor centroida klaster ne odgovara prirodnom klasteru (može da sadrži više prirodnih ali i jedan prirodni klaster može da se razbije na više ) Nedostaje specifična funkcija objekta kojom može da se izrazi postupak Nema garancije za konvergenciju, mada u praksi često konvergira snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.130
131 snovani na sakupljajućeg razdvajajućeg snovani na Spoljašnji kriterijumi 6.131
Mere slicnosti
Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
Drveta odlucivanja - algoritmi
Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Uvod Algoritmi (Iterative Dichotomiser 3) C5.0 (Classification And Regression Trees) (CHi-squared Automatic Interaction Detection) Exhaustive (Quick,
PowerPoint Presentation
Факултет организационих наука Центар за пословно одлучивање Системи за препоруку П8: Системи за препоруку Закључивање на основу случајева Системи за препоруку 2 Закључивање на основу случајева ПРОНАЂЕНО
08 RSA1
Преглед ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције RSA алгоритам Биће објашњено: RSA алгоритам алгоритам прорачунски аспекти ефикасност коришћењем јавног кључа генерисање кључа сигурност проблем
Uvod u statistiku
Uvod u statistiku Osnovni pojmovi Statistika nauka o podacima Uključuje prikupljanje, klasifikaciju, prikaz, obradu i interpretaciju podataka Staistička jedinica objekat kome se mjeri neko svojstvo. Svi
Verovatnoća - kolokvijum 17. decembar Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je
Verovatnoća - kolokvijum 17. decembar 2016. 1. Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je 0.8. Ako je ispit težak, verovatnoća da se prvo pitanje
P11.3 Analiza zivotnog veka, Graf smetnji
Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
PowerPoint Presentation
Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Classroom Expectations
АТ-8: Терминирање производно-технолошких ентитета Проф. др Зоран Миљковић Садржај Пројектовање флексибилних ; Математички модел за оптимизацију флексибилних ; Генетички алгоритми у оптимизацији флексибилних
PRIRODNO MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA RAČUNARSKE NAUKE Utorak, godine PRIJEMNI ISPIT IZ INFORMATIKE 1. Koja od navedenih ekste
PRIRODNO MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA RAČUNARSKE NAUKE Utorak, 5.06.019. godine PRIJEMNI ISPIT IZ INFORMATIKE 1. Koja od navedenih ekstenzija se najčešće koristi za tekstualne datoteke? a)
PowerPoint Presentation
Nedjelja 6 - Lekcija Projiciranje Postupci projiciranja Projiciranje je postupak prikazivanja oblika nekog, u opštem slučaju trodimenzionalnog, predmeta dvodimenzionalnim crtežom. Postupci projiciranja
Рачунарска интелигенција
Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
ТЕОРИЈА УЗОРАКА 2
ТЕОРИЈА УЗОРАКА 2 12. 04. 13. ВЕЖБАЊА Написати функције за бирање елемената популације обима N у узорак обима n, код простог случајног узорка, користећи алгоритме: Draw by draw procedure for SRS/SRSWOR
Slide 1
Statistička analiza u hidrologiji Uvod Statistička analiza se primenjuje na podatke osmatranja hidroloških veličina (najčešće: protoka i kiša) Cilj: opisivanje veze između veličine i verovatnoće njene
P9.1 Dodela resursa, Bojenje grafa
Фаза доделе ресурса Ова фаза се у литератури назива и фазом доделе регистара, при чему се под регистрима подразумева скуп ресурса истог типа. Додела регистара променљивама из графа сметњи се обавља тзв.
Tеорија одлучивања
Tеорија одлучивања Аналитички хијерархијски процес Циљ предавања Упознавање са АХП медотом Врсте АХП методе Предности и недостаци АХП методе Софтвери АХП Expert Choice MakeItRational (.com) Пример АХП
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Драган Пејић, Бојан Вујичић, Небојша Пјевалица,
Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odr
Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odrediti njene krajeve. b) Odrediti sledeće skupove: -
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аут
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Иван Жупунски, Небојша Пјевалица, Марјан Урекар,
Tutoring System for Distance Learning of Java Programming Language
Niz (array) Nizovi Niz je lista elemenata istog tipa sa zajedničkim imenom. Redosled elemenata u nizovnoj strukturi je bitan. Konkretnom elementu niza pristupa se preko zajedničkog imena niza i konkretne
Slide 1
Merni sistemi u računarstvu, http://automatika.etf.rs/sr/13e053msr Merna nesigurnost tipa A doc. dr Nadica Miljković, kabinet 68, nadica.miljkovic@etf.rs Prezentacija za ovo predavanje je skoro u potpunosti
PowerPoint Presentation
Data mining kocepti i tehnike Udžbenik: Data Mining: Concepts and Techniques, Jiawei Han, Micheline Kamber Introduction to Data Mining, Pang-Ning Tan, Michael Steinbach, Vipin Kumar Ocjenjivanje: kolokvijumi
Metode izbora lokacije
Metode izbora lokacije Metode ocenjivanja lokacija Metod bodovnog ocenjivanja Metod ponderisanja faktora Center of gravity metod Break-even analiza lokacija Transportni model Metod bodovnog ocenjivanja
Рационални Бројеви Скуп рационалних бројева 1. Из скупа { 3 4, 2, 4, 11, 0, , 1 5, 12 3 } издвој подскуп: а) природних бројева; б) целих броје
Рационални Бројеви Скуп рационалних бројева. Из скупа {,,,, 0,,, } издвој подскуп: а) природних бројева; б) целих бројева; в) ненегативних рационалних бројева; г) негативних рационалних бројева.. Запиши
Programiranje u C-u ili C++-u Pseudo-slučajni brojevi; Dinamička alokacija memorije 1 ZADACI SA ČASA Zadatak 1 Napraviti funkciju koja generišlučajan
Programiranje u C-u ili C++-u Pseudo-slučajni brojevi; Dinamička alokacija memorije 1 ZADACI SA ČASA Zadatak 1 Napraviti funkciju koja generišlučajan realan broj od 0 i 1. Na standardni izlaz ispisati
Техничко решење: Софтвер за симулацију стохастичког ортогоналног мерила сигнала, његовог интеграла и диференцијала Руководилац пројекта: Владимир Вуји
Техничко решење: Софтвер за симулацију стохастичког ортогоналног мерила сигнала, његовог интеграла и диференцијала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Велибор
Funkcije predavač: Nadežda Jakšić
Funkcije predavač: Nadežda Jakšić funkcije delovi programa koji izvršavaju neki zadatak, celinu; dele na ugrađene, korisničke i main funkciju ugrađene funkcije printf,scanf... da bi se one izvršile potrebno
Funkcije predavač: Nadežda Jakšić
Funkcije predavač: Nadežda Jakšić do sada su korišćene "gotove" funkcije iz standardnih biblioteka (cin, cout...) one su pozivane iz main funkcije koja je glavna funkcija u programu jer izvršavanje programa
Microsoft Word - ETH2_EM_Amperov i generalisani Amperov zakon - za sajt
Полупречник унутрашњег проводника коаксијалног кабла је Спољашњи проводник је коначне дебљине унутрашњег полупречника и спољашњег Проводници кабла су начињени од бакра Кроз кабл протиче стална једносмерна
PowerPoint Presentation
Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Sa stanovišta pristupa problemu korišćenja kapaciteta, razlikuju se metode
Microsoft PowerPoint - vezbe 4. Merenja u telekomunikacionim mrežama
Merenja u telekomunikacionim mrežama Merenja telefonskog saobraćaja Primer 1 - TCBH Na osnovu najviših vrednosti intenziteta saobraćaja datih za 20 mernih dana (tabela), pomoću metode TCBH, pronaći čas
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
Slide 1
Анализа електроенергетских система -Прорачун кратких спојева- Кратак спој представља поремећено стање мреже, односно поремећено стање система. За време трајања кратког споја напони и струје се мењају са
DUBINSKA ANALIZA PODATAKA
DUBINSKA ANALIZA PODATAKA () ASOCIJACIJSKA PRAVILA (ENGL. ASSOCIATION RULE) Studeni 2018. Mario Somek SADRŽAJ Asocijacijska pravila? Oblici učenja pravila Podaci za analizu Algoritam Primjer Izvođenje
Ravno kretanje krutog tela
Ravno kretanje krutog tela Brzine tačaka tela u reprezentativnom preseku Ubrzanja tačaka u reprezentativnom preseku Primer određivanja brzina i ubrzanja kod ravnog mehanizma Ravno kretanje krutog tela
Microsoft Word - AIDA2kolokvijumRsmerResenja.doc
Konstrukcija i analiza algoritama 2 (prvi kolokvijum, smer R) 1. a) Konstruisati AVL stablo od brojeva 100, 132, 134, 170, 180, 112, 188, 184, 181, 165 (2 poena) b) Konkatenacija je operacija nad dva skupa
untitled
ОСНА СИМЕТРИЈА 1. Заокружи слово испред цртежа на коме су приказане две фигуре које су осносиметричне у односу на одговарајућу праву. 2. Нацртај фигуре које су осносиметричне датим фигурама у односу на
PowerPoint Presentation
Podaci za Data Mining Glava _. Sadržaj Skupovi podataka Atributi i tipovi atributa Tipovi skupova podataka Kvalitet podataka Mjerenje sličnosti u skupu podataka Analiza na osnovu veza u podacima 10 Skupovi
Kombinatorno testiranje
Kombinatorno testiranje Uvod Na ponašanje aplikacije utiče puno faktora, npr. ulazne vrednosti, konfiguracije okruženja. Tehnike kao što je podela na klase ekvivalencije ili analiza graničnih vrednosti
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Nina Šunjo VIŠESTRUKA REGRESIJA I PROGNOZA UKUPNE AKCIJSKE PRODAJE Diploms
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Nina Šunjo VIŠESTRUKA REGRESIJA I PROGNOZA UKUPNE AKCIJSKE PRODAJE Diplomski rad Zagreb, rujan, 2014. Voditelj rada: prof.dr.sc.miljenko
Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]
![Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]](/thumbs/102/154806426.jpg "Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]")
Сложеност алгоритама (Програмирање 2, глава 3, глава 4-4.3) Проблем: класа задатака истог типа Велики број различитих (коректних) алгоритама Величина (димензија) проблема нпр. количина података које треба
Математика основни ниво 1. Одреди елементе скупова A, B, C: a) б) A = B = C = 2. Запиши елементе скупова A, B, C на основу слике: A = B = C = 3. Броје
1. Одреди елементе скупова A, B, C: a) б) A = B = C = 2. Запиши елементе скупова A, B, C на основу слике: A = B = C = 3. Бројеве записане римским цифрама запиши арапским: VIII LI XXVI CDXLIX MDCLXVI XXXIX
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe, očekuje se da su koordinate celobrojne. U slučaju
Microsoft PowerPoint - jkoren10.ppt
Dickey-Fuller-ov test jediničnog korena Osnovna ideja Različite determinističke komponente Izračunavanje test-statistike Pravilo odlučivanja Određivanje broja jediničnih korena Algoritam testiranja Prošireni
1
Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Microsoft Word - 13pavliskova
ПОДЗЕМНИ РАДОВИ 4 (5) 75-8 UDK 6 РУДАРСКО-ГЕОЛОШКИ ФАКУЛТЕТ БЕОГРАД YU ISSN 5494 ИЗВОД Стручни рад УПОТРЕБА ОДВОЈЕНОГ МОДЕЛА РЕГЕНЕРАЦИЈЕ ЗА ОДРЕЂИВАЊЕ ПОУЗДАНОСТИ ТРАНСПОРТНЕ ТРАКЕ Павлисковá Анна, Марасовá
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K.
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K. Elementi a k K su koeficijenti polinoma P (x). Ako
Р273 Пројектовање база података Примери питања за колоквијум 1. Навести најважније моделе података кроз историју рачунарства до данас. 2. Објаснити ос
Р273 Пројектовање база података Примери питања за колоквијум 1. Навести најважније моделе података кроз историју рачунарства до данас. 2. Објаснити основне концепте мрежног модела 3. Објаснити основне
Microsoft PowerPoint - C-4-1
Pregled iskaza u C-u Izraz; Iskaz dodele, serijski komponovani iskaz; blok Uslovni iskazi i izrazi; složeno grananje Iterativni iskazi Iskaz dodele Promena vrednosti a = Ψ; Izračunava vrednost izraza Ψ,
Analiticka geometrija
Analitička geometrija Predavanje 3 Konusni preseci (krive drugog reda, kvadratne krive) Novi Sad, 2018. Milica Žigić (PMF, UNS 2018) Analitička geometrija predavanje 3 1 / 22 Ime s obzirom na karakteristike
Matematka 1 Zadaci za vežbe Oktobar Uvod 1.1. Izračunati vrednost izraza (bez upotrebe pomoćnih sredstava): ( ) [ a) : b) 3 3
Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
РЕШЕЊА 1. (2) Обележја статистичких јединица посматрања су: а) особине које су заједничке за јединице посматрања б) особине које се проучавају, а подр
РЕШЕЊА. () Обележја статистичких јединица посматрања су: а) особине које су заједничке за јединице посматрања б) особине које се проучавају, а подразумевају различите вредности по јединицама посматрања
My_ST_FTNIspiti_Free
ИСПИТНИ ЗАДАЦИ СУ ГРУПИСАНИ ПО ТЕМАМА: ЛИМЕСИ ИЗВОДИ ФУНКЦИЈЕ ЈЕДНЕ ПРОМЕНЉИВЕ ИСПИТИВАЊЕ ТОКА ФУНКЦИЈЕ ЕКСТРЕМИ ФУНКЦИЈЕ СА ВИШЕ ПРОМЕНЉИВИХ 5 ИНТЕГРАЛИ ДОДАТАК ФТН Испити С т р а н а Лимеси Одредити
2015_k2_z12.dvi
OBLIKOVANJE I ANALIZA ALGORITAMA 2. kolokvij 27. 1. 2016. Skice rješenja prva dva zadatka 1. (20) Zadano je n poslova. Svaki posao je zadan kao vremenski interval realnih brojeva, P i = [p i,k i ],zai
Model podataka
Fakultet organizacionih nauka Uvod u informacione sisteme Doc. Dr Ognjen Pantelić Modeliranje podataka definisanje strategije snimanje postojećeg stanja projektovanje aplikativno modeliranje implementacija
The Contemporary Systems Development Project Landscape
Budući projektni ciklusi u Evropi Horizon Europe, nakon Horizon 2020 Program za period 2021-2027 Oko 100 milijardi ulaganja u istraživanja i inovativne programe Glavne osobine: Jačanje nauke i tehnologije
Algoritmi
Projektovanje algoritama L09.1. Topološko sortiranje Današnje teme Topološko sortiranje Povezanost grafa jako povezane komponente Minimum Spanning Trees (razapinjuće stablo) Lektira: 22. Elementary Graph
Projektovanje informacionih sistema i baze podataka
Realni sistem i informacioni sistem Ulaz Realni sistem Izlaz Unos Baza podataka Izveštaji Realni sistem i informacioni sistem Sistem se definiše kao skup objekata (entiteta) i njihovih međusobnih veza
QFD METODA – PRIMER
QFD METODA - PRIMER PROBLEM: U kompaniji X koja se bavi izradom kompjuterskih softvera uočen je pad prodaje konkretnog softvera - Softver za vođenje knjigovodstva. Kompanija X je raspolagala sa jednom
Osnovni pojmovi teorije verovatnoce
Osnovni pojmovi teorije verovatnoće Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2019 Milan Merkle Osnovni pojmovi ETF Beograd 1 / 13 Verovatnoća i statistika:
VEŽBA 5: KLASE I OBJEKTI U C# Cilj ove vežbe je upoznavanje sa osnovama rada sa klasama i objektima u programskom jeziku C#. Pored toga, bide demonstr
VEŽBA 5: KLASE I OBJEKTI U C# Cilj ove vežbe je upoznavanje sa osnovama rada sa klasama i objektima u programskom jeziku C#. Pored toga, bide demonstrirana upotreba konstruktora, svojstava, metoda klase,
Problemi zadovoljavanja ogranicenja.
I122 Osnove umjetne inteligencije Tema:. 7.1.2016. predavač: Darija Marković asistent: Darija Marković 1 I122 Osnove umjetne inteligencije. 2/26 (PZO) Problem zadovoljavanja ograničenja sastoji se od 3
STABILNOST SISTEMA
STABILNOST SISTEMA Najvaznija osobina sistema automatskog upravljanja je stabilnost. Generalni zahtev koji se postavlja pred projektanta jeste da projektovani i realizovani sistem automatskog upravljanja
NAPOMENA: Studenti na ispit donose kod urađenog zadatka
Пројекат из предмета Интернет програмирање за августовски и септембарски испитни рок школске 2018/19. године Коришћењем PHP технологије, технологије AJAX и MySQL базе података, реализовати следећу веб
Konstrukcija i analiza algoritama vežbe 10 Nina Radojičić 15. decembar Algoritamske strategije - podeli pa vladaj (divide and conquer) Ova stra
Konstrukcija i analiza algoritama vežbe 10 Nina Radojičić 15. decembar 2016 1 Algoritamske strategije - podeli pa vladaj (divide and conquer) Ova strategija rekurzivno razbija problem na 2 ili više potproblema
MIP-heuristike (Matheuristike) Hibridi izmedu metaheurističkih i egzaktnih metoda Tatjana Davidović Matematički institut SANU
MIP-heuristike (Matheuristike) Hibridi izmedu metaheurističkih i egzaktnih metoda Tatjana Davidović Matematički institut SANU http://www.mi.sanu.ac.rs/ tanjad (tanjad@mi.sanu.ac.rs) 21. januar 2013. Tatjana
Прва економска школа Београд РЕПУБЛИЧКО ТАКМИЧЕЊЕ ИЗ СТАТИСТИКЕ март године ОПШТЕ ИНФОРМАЦИЈЕ И УПУТСТВО ЗА РАД Укупан број такмичарских
Прва економска школа Београд РЕПУБЛИЧКО ТАКМИЧЕЊЕ ИЗ СТАТИСТИКЕ 9-30. март 019. године ОПШТЕ ИНФОРМАЦИЈЕ И УПУТСТВО ЗА РАД Укупан број такмичарских задатака је 10. Број поена за сваки задатак означен је
Slide 1
Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
Microsoft PowerPoint - Ekoloska (city) logistika 8.3
ЕКОЛОШКА (CITY) ЛОГИСТИКА Осмо предавање управљање отпадом,, пример Познато: Капацитет смећара које врши опслугу је: q m =8 t Количина отпада коју треба скупити на местима (чворова),,,,6 и 7, дат је у
Математика 1. Посматрај слику и одреди елементе скуупова: а) б) в) средњи ниво А={ } B={ } А B={ } А B={ } А B={ } B А={ } А={ } B={ } А B={ } А B={ }
1. Посматрај слику и одреди елементе скуупова: а) б) в) А={ } B={ } А B={ } А B={ } А B={ } B А={ } А={ } B={ } А B={ } А B={ } А B={ } B А={ } А={ } B={ } А B={ } А B={ } А B={ } B А={ } 2. Упиши знак
DR DRAGOŚ CVETKOVIC DR SLOBODAN SIMIC DISKRETNA MATEMATIKA MATEMATIKA ZA KOMPJUTERSKE NAUKĘ DRUGO ISPRAYLJENO I PROSIRENO IZDANJE HMUJ
DR DRAGOŚ CVETKOVIC DR SLOBODAN SIMIC DISKRETNA MATEMATIKA MATEMATIKA ZA KOMPJUTERSKE NAUKĘ DRUGO ISPRAYLJENO I PROSIRENO IZDANJE HMUJ Sadrżaj Predgovor Iz predgovora prvoni izdanju knjige "Diskretne mateiuatićke
Орт колоквијум
II колоквијум из Основа рачунарске технике I - 27/28 (.6.28.) Р е ш е њ е Задатак На улазе x, x 2, x 3, x 4 комбинационе мреже, са излазом z, долази четворобитни BCD број. Ако број са улаза при дељењу
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 018/019. година ТЕСТ МАТЕМАТИКА
Microsoft Word - Matematika_kozep_irasbeli_javitasi_0802.doc
Matematika szerb nyelven középszint 080 ÉRETTSÉGI VIZSGA 009. május 5. MATEMATIKA SZERB NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Важне
Maksimalni protok kroz mrežu - Ford-Fulkerson, Edmonds-Karp
Maksimalni protok kroz mrežu - Ford-Fulkerson, Edmonds-Karp PMF-MO Seminar iz kolegija Oblikovanje i analiza algoritama 22.1.2019. mrežu - Ford-Fulkerson, Edmonds-Karp 22.1.2019. 1 / 35 Uvod - definicije
DISKRETNA MATEMATIKA
DISKRETNA MATEMATIKA Kombinatorika Permutacije, kombinacije, varijacije, binomna formula Ivana Milosavljević - 1 - 1. KOMBINATORIKA PRINCIPI PREBROJAVANJA Predmet kombinatorike je raspoređivanje elemenata
СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за векто
![СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за векто](/thumbs/102/155791469.jpg "СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за векто")
СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за вектор a (коjи може бити и дужине нула) и неке изометриjе
Microsoft Word - CAD sistemi
U opštem slučaju, se mogu podeliti na 2D i 3D. 2D Prvo pojavljivanje 2D CAD sistema se dogodilo pre više od 30 godina. Do tada su inženjeri koristili table za crtanje (kulman), a zajednički jezik komuniciranja
Broj indeksa:
putstvo za 5. laboratorijsku vežbu Napomena: svakoj brojnoj vrednosti fizičkih veličina koje se nalaze u izveštaju obavezno pridružiti odgovarajuće jedinice, uključujući i oznake na graficima u tabelama
MATEMATIKA EKSTERNA PROVJERA ZNANJA UČENIKA NA KRAJU III CIKLUSA OSNOVNE ŠKOLE UPUTSTVO VRIJEME RJEŠAVANJA TESTA: 70 MINUTA Pribor: grafitna olovka i
MATEMATIKA EKSTERNA PROVJERA ZNANJA UČENIKA NA KRAJU III CIKLUSA OSNOVNE ŠKOLE UPUTSTVO VRIJEME RJEŠAVANJA TESTA: 70 MINUTA Pribor: grafitna olovka i gumica, hemijska olovka, geometrijski pribor. Upotreba
Postojanost boja
Korištenje distribucije osvjetljenja za ostvaranje brzih i točnih metode za postojanost boja Nikola Banić 26. rujna 2014. Sadržaj Postojanost boja Ubrzavanje lokalnog podešavanja boja Distribucija najčešćih
Microsoft PowerPoint - Predavanje3.ppt
Фрактална геометрија и фрактали у архитектури функционални системи Улаз Низ правила (функција F) Излаз Фрактална геометрија и фрактали у архитектури функционални системи Функционални систем: Улаз Низ правила
(Microsoft Word - LOCIRANJE ROBE U SKLADI\212TU-vezbe doc)
LOCIRANJE ROBE U SKLADIŠTU Skladištenje je centralna funkcija skladišta Sa aspekta ove funkcije,za robu koja se pojavljuje u skladištu, bitne su tri odluke: Koliko zaliha Koliko često i kada ove zalihe
Veeeeeliki brojevi
Matematička gimnazija Nedelja informatike 3 12. decembar 2016. Uvod Postoji 10 tipova ljudi na svetu, oni koji razumeju binarni sistem, oni koji ne razumeju binarni sistem i oni koji nisu očekivali šalu
Microsoft PowerPoint - Topic02 - Serbian.ppt
Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
Inženjering informacionih sistema
Fakultet tehničkih nauka, Novi Sad Inženjering informacionih sistema Dr Ivan Luković Dr Slavica Kordić Nikola Obrenović Milanka Bjelica Dr Jelena Borocki Dr Milan Delić UML UML (Unified Modeling Language)
EFIKASNO MODELIRANJE REALNIH OPTIMIZACIONIH PROBLEMA Tatjana Davidović Matematički institut SANU tanjad
EFIKASNO MODELIRANJE REALNIH OPTIMIZACIONIH PROBLEMA Tatjana Davidović Matematički institut SANU http://www.mi.sanu.ac.rs/ tanjad (tanjad@mi.sanu.ac.rs) VII Simpozijum,,Matematika i primene 4. novembar
Microsoft PowerPoint - Topic02 - Serbian.ppt
Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
Numeričke metode u fizici 1, Projektni zadataci 2018./ Za sustav običnih diferencijalnih jednadžbi, koje opisuju kretanje populacije dviju vrs
Numeričke metode u fizici, Projektni zadataci 8./9.. Za sustav običnih diferencijalnih jednadžbi, koje opisuju kretanje populacije dviju vrsta životinja koje se nadmeću za istu hranu, dx ( dt = x x ) xy
Sadržaj 1 Diskretan slučajan vektor Definicija slučajnog vektora Diskretan slučajan vektor
Sadržaj Diskretan slučajan vektor Definicija slučajnog vektora 2 Diskretan slučajan vektor Funkcija distribucije slučajnog vektora 2 4 Nezavisnost slučajnih vektora 2 5 Očekivanje slučajnog vektora 6 Kovarijanca
06 Poverljivost simetricnih algoritama1
ЗАШТИТА ПОДАТАКА Симетрични алгоритми заштите поверљивост симетричних алгоритама Преглед биће објашњено: коришћење симетричних алгоритама заштите како би се заштитила поверљивост потреба за добрим системом
Tutoring System for Distance Learning of Java Programming Language
Deklaracija promenljivih Inicijalizacija promenljivih Deklaracija promenljive obuhvata: dodelu simboličkog imena promenljivoj i određivanje tipa promenljive (tip određuje koja će vrsta memorijskog registra
ФАКУЛТЕТ ОРГАНИЗАЦИОНИХ НАУКА
Питања за усмени део испита из Математике 3 I. ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ 1. Појам диференцијалне једначине. Пикарова теорема. - Написати општи и нормални облик диференцијалне једначине првог реда. - Дефинисати:
УНИВЕРЗИТЕТ У НИШУ ПРИРОДНО-МАТЕМАТИЧКИ ФАКУЛТЕТ Департман за рачунарске науке Писмени део испита из предмета Увод у рачунарство 1. [7 пое
УНИВЕРЗИТЕТ У НИШУ ПРИРОДНО-МАТЕМАТИЧКИ ФАКУЛТЕТ Департман за рачунарске науке 30.06.2018. Писмени део испита из предмета Увод у рачунарство 1. [7 поена] Методом МакКласкија минимизарити систем прекидачких
OOP1 - domaci 2 (2004/05)
ЕЛЕКТРОТЕХНИЧКИ ФАКУЛТЕТ Одсеци ИР, ОС и ОФ Београд, 05.04.2019. Први домаћи задатак из Објектно оријентисаног програмирања 2 У сваком задатку: Грешке пријављивати изузецима типа класа које садрже текст
(Microsoft Word - Dr\236avna matura - studeni osnovna razina - rje\232enja)
1. C. Imamo redom: I. ZADATCI VIŠESTRUKOGA IZBORA 9 + 7 6 9 + 4 51 = = = 5.1 18 4 18 8 10. B. Pomoću kalkulatora nalazimo 10 1.5 = 63.45553. Četvrta decimala je očito jednaka 5, pa se zaokruživanje vrši
Technology management performance indicators in global country rankings
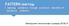PATTERN метод (Planning Assistance Through Technical Evaluation of Relevance Numbers) Менаџмент технологије и развоја 2018/19 PATTERN метод Метод нормативног предвиђања Метод стабла значајности Стабло
Paper Title (use style: paper title)
Статистичка анализа коришћења електричне енергије која за последицу има примену повољнијег тарифног става Аутор: Марко Пантовић Факултет техничких наука, Чачак ИАС Техника и информатика, 08/09 e-mal адреса:
Profajliranje ivica: Knutov algoritam i njegova unapredenja Seminarski rad u okviru kursa Verifikacija softvera Matematički fakultet Nevena Nikolić, 1
Profajliranje ivica: Knutov algoritam i njegova unapredenja Seminarski rad u okviru kursa Verifikacija softvera Matematički fakultet Nevena Nikolić, 1021/2018 nevena134@hotmail.com 9. decembar 2018 Sažetak