Kombinatorno testiranje
|
|
|
- Борут Друловић
- пре 5 година
- Прикази:
Транскрипт
1 Kombinatorno testiranje
2 Uvod Na ponašanje aplikacije utiče puno faktora, npr. ulazne vrednosti, konfiguracije okruženja. Tehnike kao što je podela na klase ekvivalencije ili analiza graničnih vrednosti identifikuju moguće vrednosti pojedinih faktora Od značaja su i kombinacije vrednosti, ali nije praktično testirati sve moguće kombinacije 2
3 Primer: servis za naručivanje pice SNP SNP prima naružbe, proverava validnost i inicira slanje pice. Mušterija mora da navede četiri podatka: veličina pice, preliv, adresa dostave i kučni broj telefona. 3
4 PDS: Model prostora ulaznih podataka Ukupan broj kombinacija vrednosti faktora je 3*2 3 =24 Drugačije vrednosti faktora bi još povećale broj kombinacija 4
5 Primer: Testiranje korisničkog interfejsa GUI aplikacije sastoji se od menija File, Edit i Format. Ima tri faktora, a svaki može da se postavi na bilo koji od 4 nivoa. Ukupno 4 3 =64 kombinacije. 5
6 Primer: sort komanda na UNIXu sort [-cmu] [-ooutput] [-Tdirectory] [-y [ kmem]] [-zrecsz] [- dfimnr] [-b] [ tchar] [-kkeydef] [+pos1[-pos2]] [file...] Može se identifikovati 20 faktora for za sort komandu. Uzimajući u obzir njihove moguće vrednosti, tj. sve nivoe, postoji oko 1.9x10 9 kombinacija. 6
7 Testiranje kompatibilnosti npr. testiranje web aplikacije na različitim platformama i browserima 3*5*5=75 kombinacija, ali nisu sve u praksi moguće 7
8 Primer otkaza usled interakcije vrednosti // pretpostavka x, y {-1, 1}, and z {0, 1} begin int x, y, z, p; input (x, y, z); p = (x + y) * z // trebalo bi da bude p = (x y) * z if (p >= 0) output (f(x, y, z)); else output (g(x, y)); end Otkaz iniciraju sve vrednosti koje zadovoljavaju x+y x-y i z 0. Međutim, otkaz otkrivaju samo dve od mogućih osam kombinacija ulaza: x=-1, y=1, z=1 i x=-1, y=-1, z=1. 8
9 Kombinatorno testiranje Umesto testiranja svih mogućih kombinacija, uzima se podskup kombinacija koji zadovoljava neku od definisanih kombinatornih strategija testiranja. Ne utiče svaki ulazni faktor na svaki otkaz, često je otkaz iniciran interakcijama malog broja faktora Zbog toga kombinatorne strategije mogu dramatično redukovati broj kombinacija koje treba pokriti ali pri tom ostaju vrlo efikasne u detekciji otkaza. 9
10 Kombinatorne strategije testiranja Pokrivanje svih kombinacija Pokrivanje svih pojedinih vrednosti Pokrivanje parova vrednosti Pokrivanje n-torki vrednosti 10
11 Pokrivanje svih kombinacija Svaka moguća kombinacija vrednosti svih ulaznih parametara mora biti pokrivena. Primer: Pretpostavimo da program koji se testira ima tri ulazne promenljive, od kojih svaka uzima jednu od dve vrednosti Neka su X, Y i Z ulazne promenljive a {X1, X2}, {Y1, Y2}, {Z1, Z2} njihovi skupovi vrednosti. Svi mogući skupovi kombinacija (2 3 ) su: 11
12 Pokrivanje svih pojedinačnih vrednosti Svaka vrednost svakog parametra mora biti pokrivena bar jedanput. Za prethodni primer, serija testova koja zadovoljava je: {(X 1,Y 1, Z 1 ), (X 2,Y 2, Z 2 )} 12
13 Pokrivanje parova vrednosti Za bilo koja dva parametra, sve kombinacije vrednosti ovih parametara moraju biti pokrivene bar u jednom test primeru Za posmatrani primer: X, Y i Z ulazne promenljive a {X1, X2}, {Y1, Y2}, {Z1, Z2} njihovi skupovi vrednosti ima 12 parova vrednosti: (X1, Y1), (X1, Y2), (X1, Z1), (X1, Z2), (X2, Y1), (X2, Y2), (X2, Z1), (X2, Z2), (Y1, Z1), (Y1, Z2), (Y2, Z1) i (Y2, Z2). 13
14 Pokrivanje parova vrednosti - primer Sledeće četiri kombinacije pokrivaju sve parove: Moguće je naći i druge skupove od četiri kombinacije koje pokrivaju svih 12 parova. Radi se o balansiranom skupu kombinacija jer se svaka vrednost svakog parametra pojavljuje tačno jednak broj puta. 14
15 Pokrivanje n-torki vrednosti Za bilo koji podskup od n parametara, sve kombinacije vrednosti tih n parametra moraju biti pokrivene bar jednim test primerom Primetiti da su prethodni kriterijumi samo specijalni slučajevi ovog najopštijeg kriterijuma 15
16 Konstrukcija kombinatornih tabela Metodi zasnovani na pretrazi u prostoru stanja uglavnom razvijaju računarci AETG (from Telcordia), TCG (from JPL/NASA), DDA (from ASU), PairTest Algebarski metodi koje su razvili matematičari Ortogonalni nizovi (orthogonal arrays) Pokrivajući nizovi (covering arrays) 16
17 Ortogonalni nizovi OA(N, k, s, t) N=4 kombinacija (runs) k=3 faktora s=2 vrednosti (levels, symbols) t=2 jačina (strength) Ortogonalni niz je N x k matrica popunjena vrednostima iz konačnog skupa od s simbola, sa svojstvom (balansa) da bilo koja N x t podmatrica sadrži proizvoljnu t-torku vrednosti uvek isti broj puta.. Taj broj naziva se indeks ortogonalnog niza i računa kao = N / s t 17
18 Ortogonalni nizovi: Indeks OA(4, 3, 2, 2) N=4 kombinacija (runs) k=3 faktora s=2 vrednosti (levels, symbols) t=2 jačina (strength) = N/s t = 4/2 2 =1 što znači da se svaki par pojavljuje tačno jednom u bilo kome 4x2 podnizu. Ima ukupno s t =2 2 =4 para: (1, 1), (1, 2), (2, 1), (2, 2). 18
19 Ortogonalni nizovi: drugi primer OA(9, 4, 3, 2) OA(runs, factors, levels, strength) indeks =1. 19
20 Ortogonalni nizovi: Alternativno obeležavanje Ortogonalni niz sa N kombinacija gde k faktora uzima neku od s vrednosti. L 4 (2 3 ) L 9 (3 4 ) 20
21 Konstrukcija OA koristeći polje Galoa Aritmetika po modulu 3, sabiranje i množenje GF(3) x Zameniti svaku nulu u tabeli množenja nultom kolonom tabele sabiranja. Isto to uraditi sa 1 i 2 i odgovarajućim kolonama. Tako ćemo dobiti OA sa 9 redova i tri kolone 21
22 Ortogonalni niz L 9 (3 3 ) Zamenili smo svaki element x tabele odgovarajućom kolonom + tabele L 9 (3 3 ) x
23 Dobijanje ortogonalnog niza L 9 (3 4 ) Dodati jednu kolonu. Popuniti tako da svaka tri reda promenimo vrednost u njoj dok se ne izređaju sve tri vrednosti
24 OA mešovitih nivoa (Mixed level Orthogonal arrays) Prethodni OA bili su sa fiksnim nivoom, što znači da su svi faktori uzimali vrednosti iz istog skupa. U praktičnoj primeni faktori uzimaju vrednosti iz različitih skupova. Obeležavanje: Strength=t. Runs=N. k1 faktora ima s1 nivoa, k2 ima s2 nivoa, itd. Ukupan broj faktora: 24
25 OA mešovitih nivoa (nastavak) Osobina balansa za ove nizove takođe važi, tj. bilo koja N x t podmatrica sadrži proizvoljnu t-torku vrednosti, uvek isti broj puta, a taj broj je. Indeks ne može se međutim računati po ranije navedenoj formuli. 25
26 OA mešovitih nivoa: Primer Balans: U bilo kojoj podmatrici 8 x 2, svaki par vrednosti (strength=2) pojavljuje se tačno jednom. 26
27 Generisanje testova na osnovu MA: Primer dostave pice Postoje 3 binarna faktora i jedan faktor sa 3 nivoa. U skladu sa tim upotrebićemo sledeći niz: 27
28 Generisanje testova na osnovu MA: Primer dostave pice Svi postojeći parovi vrednosti faktora su pokriveni. 28
29 Generisanje testova na osnovu MA: Primer dostave pice Testovi 29
30 Pokrivajući nizovi Pokrivajući niz CA(N, k, s, t) je N x k matrica sa ulazima iz konačnog skupa od s symbola tako da svaka N x t podmatrica sadrži svaku moguću t-torku najmanje puta. N broj kombinacija (runs), k broj faktora, s broj nivoa za faktore, t je jačina, a je indeks. CA su generalizacija OA. Svaki OA je CA, ali obrnuto ne važi. Za potrebe generisanja softverskih testova, razmatramo samo =1. Za razliku od OA, CA nisu balansirani i zato obično imaju manje N za iste ostale faktore. 30
31 Pokrivajući nizovi: Primer Balansirani OA jačine 2 za 5 binarnih faktora, zahteva 8 kombinacija. Međutim, CA istih karakteristika zahteva samo 6. 31
32 Pokrivajući nizovi sa mešovitim nivoima Pokrivajući niz sa mešovitim nivoima označava se kao i i odnosi na N x Q matricu tako da važi i i 1 svaka N x t podmatrica sadrži bar jednu pojavu svake t- torke vrednosti. s1, s2, označavaju broj nivoa za svaki odgovarajući faktor. Q p k 32
33 Pokrivajući nizovi sa mešovitim nivoima: Primer MCA su generalno manji od MOA i samim tim pogodniji za upotrebu u testiranju. U poređenju sa ranijim uočava se redukcija za 6 kombinacija. Is the above array balanced? 33
34 Konstrukcija CA: Terminologija N-tostruka serija testova -> N-tostruki pokrivajući niz Testovi -> Redovi Parametri -> Faktori ili kolone Vrednosti -> Nivoi (Levels) 34
35 In Parameter Order Strategija Konstruiše t-struku seriju testova na inkrementalni način t-struka serija testova se konstruiše za prvih t parametara, Onda se serija testova proširuje da generiše t- struku seriju testova za prvih t + 1 parametara Prethodni koraci se ponavljaju za svaki sledeći parametar U svakom proširenju za novi parametar preduzimaju se dva koraka: Horizontalni rast: proširuje svaki postojeći test dodajuči jednu vrednost za novi parametar Vertikalni rast: dodati novi test, ako je to potrebno 35
36 IPO strategija (nastavak) Strategy In-Parameter-Order begin /* for the first t parameters p 1, p 2,, p t */ T := {(v 1, v 2,, v t ) v 1, v 2,, v t are values of p 1, p 2,, P k, respectively} if n = t then stop; /* for the remaining parameters */ for parameter p i, i = t + 1,, n do begin /* horizontal growth */ for each test (v 1, v 2,, v i-1 ) in T do replace it with (v 1, v 2,, v i-1, v i ), where v i is a value of p i /* vertical growth */ while T does not cover all the interactions between p i and each of p 1, p 2,, p i-1 do add a new test for p 1, p 2,, p i to T; end end 36
37 Primer Razmotrimo sistem sa sledećim parametrima: parametar A ima vrednosti A1 i A2 parametar B ima vrednosti B1 i B2 parametar C ima vrednosti C1, C2 i C3 37
38 Primer (nastavak) A B A1 B1 A1 B2 A2 B1 A2 B2 A B C A1 B1 C1 A1 B2 C2 A2 B1 C3 A2 B2 C1 Horizontalni rast A B C A1 B1 C1 A1 B2 C2 A2 B1 C3 A2 B2 C1 A2 B1 C2 A1 B2 C3 Vertikalni rast 38
Inženjering informacionih sistema
 Fakultet tehničkih nauka, Novi Sad Inženjering informacionih sistema Dr Ivan Luković Dr Slavica Kordić Nikola Obrenović Milanka Bjelica Dr Jelena Borocki Dr Milan Delić UML UML (Unified Modeling Language)
Fakultet tehničkih nauka, Novi Sad Inženjering informacionih sistema Dr Ivan Luković Dr Slavica Kordić Nikola Obrenović Milanka Bjelica Dr Jelena Borocki Dr Milan Delić UML UML (Unified Modeling Language)
MIP-heuristike (Matheuristike) Hibridi izmedu metaheurističkih i egzaktnih metoda Tatjana Davidović Matematički institut SANU
 MIP-heuristike (Matheuristike) Hibridi izmedu metaheurističkih i egzaktnih metoda Tatjana Davidović Matematički institut SANU http://www.mi.sanu.ac.rs/ tanjad (tanjad@mi.sanu.ac.rs) 21. januar 2013. Tatjana
MIP-heuristike (Matheuristike) Hibridi izmedu metaheurističkih i egzaktnih metoda Tatjana Davidović Matematički institut SANU http://www.mi.sanu.ac.rs/ tanjad (tanjad@mi.sanu.ac.rs) 21. januar 2013. Tatjana
Skripte2013
 Chapter 2 Algebarske strukture Preslikivanje f : A n! A se naziva n-arna operacija na skupu A Ako je n =2, kažemo da je f : A A! A binarna operacija na A Kažemo da je operacija f arnosti n, u oznaci ar
Chapter 2 Algebarske strukture Preslikivanje f : A n! A se naziva n-arna operacija na skupu A Ako je n =2, kažemo da je f : A A! A binarna operacija na A Kažemo da je operacija f arnosti n, u oznaci ar
QFD METODA – PRIMER
 QFD METODA - PRIMER PROBLEM: U kompaniji X koja se bavi izradom kompjuterskih softvera uočen je pad prodaje konkretnog softvera - Softver za vođenje knjigovodstva. Kompanija X je raspolagala sa jednom
QFD METODA - PRIMER PROBLEM: U kompaniji X koja se bavi izradom kompjuterskih softvera uočen je pad prodaje konkretnog softvera - Softver za vođenje knjigovodstva. Kompanija X je raspolagala sa jednom
Орт колоквијум
 II колоквијум из Основа рачунарске технике I - 27/28 (.6.28.) Р е ш е њ е Задатак На улазе x, x 2, x 3, x 4 комбинационе мреже, са излазом z, долази четворобитни BCD број. Ако број са улаза при дељењу
II колоквијум из Основа рачунарске технике I - 27/28 (.6.28.) Р е ш е њ е Задатак На улазе x, x 2, x 3, x 4 комбинационе мреже, са излазом z, долази четворобитни BCD број. Ако број са улаза при дељењу
1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan
 1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan jednačinom oblika: a 11 x 2 + 2a 12 xy + a 22 y 2
1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan jednačinom oblika: a 11 x 2 + 2a 12 xy + a 22 y 2
Microsoft Word - MySQL_3.doc
 7. Data Manipulation Language (DML) Jezik za rad sa podacima (Data Manipulation Language (DML)) služi za umetanje, brisanje i ažuriranje podataka u bazi. 7.1. Umetanje novih redova u tabelu INSERT sintaksa
7. Data Manipulation Language (DML) Jezik za rad sa podacima (Data Manipulation Language (DML)) služi za umetanje, brisanje i ažuriranje podataka u bazi. 7.1. Umetanje novih redova u tabelu INSERT sintaksa
JMBAG IME I PREZIME BROJ BODOVA MJERA I INTEGRAL 2. kolokvij 29. lipnja (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni!) 1. (
 MJERA I INTEGRAL. kolokvij 9. lipnja 018. (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni! 1. (ukupno 6 bodova Neka je (, F, µ prostor s mjerom, neka je (f n n1 niz F-izmjerivih funkcija
MJERA I INTEGRAL. kolokvij 9. lipnja 018. (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni! 1. (ukupno 6 bodova Neka je (, F, µ prostor s mjerom, neka je (f n n1 niz F-izmjerivih funkcija
Microsoft Word - 15ms261
 Zadatak 6 (Mirko, elektrotehnička škola) Rješenje 6 Odredite sup S, inf S, ma S i min S u skupu R ako je S = { R } a b = a a b + b a b, c < 0 a c b c. ( ), : 5. Skratiti razlomak znači brojnik i nazivnik
Zadatak 6 (Mirko, elektrotehnička škola) Rješenje 6 Odredite sup S, inf S, ma S i min S u skupu R ako je S = { R } a b = a a b + b a b, c < 0 a c b c. ( ), : 5. Skratiti razlomak znači brojnik i nazivnik
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica
 Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe
 6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe, očekuje se da su koordinate celobrojne. U slučaju
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe, očekuje se da su koordinate celobrojne. U slučaju
Microsoft PowerPoint - Strukturni dijagrami, Gantogram - Planiranje [Compatibility Mode]
![Microsoft PowerPoint - Strukturni dijagrami, Gantogram - Planiranje [Compatibility Mode] Microsoft PowerPoint - Strukturni dijagrami, Gantogram - Planiranje [Compatibility Mode]](/thumbs/99/139496506.jpg) + Metode i tehnike planiranja projekta + Projektne strukture + Tehnike struktuiranja projekta Breakdow strukture strukture za dekomponovanje Matrice WBS: Project Work Breakdown Structure OBS: Organization
+ Metode i tehnike planiranja projekta + Projektne strukture + Tehnike struktuiranja projekta Breakdow strukture strukture za dekomponovanje Matrice WBS: Project Work Breakdown Structure OBS: Organization
P1.3 Projektovanje makroasemblera
 ПРОЈЕКТОВАЊЕ МАКРОАСЕМБЛЕРА Макроасемблер Потребна проширења асемблера 1 МАКРОАСЕМБЛЕР Макроасемблер преводи полазни програм написан на макроасемблерском језику у извршиви машински програм. Приликом израде
ПРОЈЕКТОВАЊЕ МАКРОАСЕМБЛЕРА Макроасемблер Потребна проширења асемблера 1 МАКРОАСЕМБЛЕР Макроасемблер преводи полазни програм написан на макроасемблерском језику у извршиви машински програм. Приликом израде
Рачунарска интелигенција
 Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Microsoft PowerPoint - vezbe 4. Merenja u telekomunikacionim mrežama
 Merenja u telekomunikacionim mrežama Merenja telefonskog saobraćaja Primer 1 - TCBH Na osnovu najviših vrednosti intenziteta saobraćaja datih za 20 mernih dana (tabela), pomoću metode TCBH, pronaći čas
Merenja u telekomunikacionim mrežama Merenja telefonskog saobraćaja Primer 1 - TCBH Na osnovu najviših vrednosti intenziteta saobraćaja datih za 20 mernih dana (tabela), pomoću metode TCBH, pronaći čas
Microsoft Word - CAD sistemi
 U opštem slučaju, se mogu podeliti na 2D i 3D. 2D Prvo pojavljivanje 2D CAD sistema se dogodilo pre više od 30 godina. Do tada su inženjeri koristili table za crtanje (kulman), a zajednički jezik komuniciranja
U opštem slučaju, se mogu podeliti na 2D i 3D. 2D Prvo pojavljivanje 2D CAD sistema se dogodilo pre više od 30 godina. Do tada su inženjeri koristili table za crtanje (kulman), a zajednički jezik komuniciranja
Paper Title (use style: paper title)
 Статистичка анализа коришћења електричне енергије која за последицу има примену повољнијег тарифног става Аутор: Марко Пантовић Факултет техничких наука, Чачак ИАС Техника и информатика, 08/09 e-mal адреса:
Статистичка анализа коришћења електричне енергије која за последицу има примену повољнијег тарифног става Аутор: Марко Пантовић Факултет техничких наука, Чачак ИАС Техника и информатика, 08/09 e-mal адреса:
Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]
![Microsoft PowerPoint - 03-Slozenost [Compatibility Mode] Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]](/thumbs/102/154806426.jpg) Сложеност алгоритама (Програмирање 2, глава 3, глава 4-4.3) Проблем: класа задатака истог типа Велики број различитих (коректних) алгоритама Величина (димензија) проблема нпр. количина података које треба
Сложеност алгоритама (Програмирање 2, глава 3, глава 4-4.3) Проблем: класа задатака истог типа Велики број различитих (коректних) алгоритама Величина (димензија) проблема нпр. количина података које треба
Primenjeno programiranje - Vežbe
 VISOKA POSLOVNA ŠKOLA STRUKOVNIH STUDIJA NOVI SAD Primena integrisanih razvojnih alata Java i NetBeans IDE 7.0 vežba 9 i 10 Kreiranje desktop aplikacije sa konekcijom na bazu Pokrenuti NetBeans, u kartici
VISOKA POSLOVNA ŠKOLA STRUKOVNIH STUDIJA NOVI SAD Primena integrisanih razvojnih alata Java i NetBeans IDE 7.0 vežba 9 i 10 Kreiranje desktop aplikacije sa konekcijom na bazu Pokrenuti NetBeans, u kartici
PowerPoint Presentation
 Prof. dr Pere Tumbas Prof. dr Predrag Matkovid Identifikacija i izbor projekata Održavanje sistema Inicijalizacija projekata i planiranje Implementacija sistema Dizajn sistema Analiza sistema Faze životnog
Prof. dr Pere Tumbas Prof. dr Predrag Matkovid Identifikacija i izbor projekata Održavanje sistema Inicijalizacija projekata i planiranje Implementacija sistema Dizajn sistema Analiza sistema Faze životnog
Microsoft Word - Predmet 6-Primjena upravljackog racunovodstva maj 2019 RJESENJE
 I ТЕСТ ПIТАЊА КОМИСИЈА ЗА РАЧУНОВОДСТВО И РЕВИЗИЈУ БОСНЕ И ХЕРЦЕГОВИНЕ ИСПИТ ЗА СТИЦАЊЕ ПРОФЕСИОНАЛНОГ ЗВАЊА СЕРТИФИКОВАНИ РАЧУНОВОЂА (ИСПИТНИ ТЕРМИН: МАЈ 2019. ГОДИНЕ) ПРЕДМЕТ 6: ПРИМЈЕНА УПРАВЉАЧКОГ
I ТЕСТ ПIТАЊА КОМИСИЈА ЗА РАЧУНОВОДСТВО И РЕВИЗИЈУ БОСНЕ И ХЕРЦЕГОВИНЕ ИСПИТ ЗА СТИЦАЊЕ ПРОФЕСИОНАЛНОГ ЗВАЊА СЕРТИФИКОВАНИ РАЧУНОВОЂА (ИСПИТНИ ТЕРМИН: МАЈ 2019. ГОДИНЕ) ПРЕДМЕТ 6: ПРИМЈЕНА УПРАВЉАЧКОГ
Орт колоквијум
 Испит из Основа рачунарске технике - / (6.6.. Р е ш е њ е Задатак Комбинациона мрежа има пет улаза, по два за број освојених сетова тенисера и један сигнал који одлучује ко је бољи уколико је резултат
Испит из Основа рачунарске технике - / (6.6.. Р е ш е њ е Задатак Комбинациона мрежа има пет улаза, по два за број освојених сетова тенисера и један сигнал који одлучује ко је бољи уколико је резултат
Microsoft Word - 1.Operacije i zakoni operacija
 1. Operacije i zakoni operacija Neka je S neprazan skup. Operacija dužine n skupa S jeste svako preslikavanje : n n f S S ( S = S S S... S) Ako je n = 1, onda operaciju nazivamo unarna. ( f : S S ) Ako
1. Operacije i zakoni operacija Neka je S neprazan skup. Operacija dužine n skupa S jeste svako preslikavanje : n n f S S ( S = S S S... S) Ako je n = 1, onda operaciju nazivamo unarna. ( f : S S ) Ako
PowerPoint Presentation
 Visoka škola strukovnih studija za informacione i komunikacione tehnologije MVC - Modeli Školska 2017/18. Dr Nenad Kojić, dipl. inž. Luka Lukić, struk. inž. Danijela Nikitin, spec.stuk.inž MVC.htaccess
Visoka škola strukovnih studija za informacione i komunikacione tehnologije MVC - Modeli Školska 2017/18. Dr Nenad Kojić, dipl. inž. Luka Lukić, struk. inž. Danijela Nikitin, spec.stuk.inž MVC.htaccess
Microsoft PowerPoint - C-4-1
 Pregled iskaza u C-u Izraz; Iskaz dodele, serijski komponovani iskaz; blok Uslovni iskazi i izrazi; složeno grananje Iterativni iskazi Iskaz dodele Promena vrednosti a = Ψ; Izračunava vrednost izraza Ψ,
Pregled iskaza u C-u Izraz; Iskaz dodele, serijski komponovani iskaz; blok Uslovni iskazi i izrazi; složeno grananje Iterativni iskazi Iskaz dodele Promena vrednosti a = Ψ; Izračunava vrednost izraza Ψ,
My_ST_FTNIspiti_Free
 ИСПИТНИ ЗАДАЦИ СУ ГРУПИСАНИ ПО ТЕМАМА: ЛИМЕСИ ИЗВОДИ ФУНКЦИЈЕ ЈЕДНЕ ПРОМЕНЉИВЕ ИСПИТИВАЊЕ ТОКА ФУНКЦИЈЕ ЕКСТРЕМИ ФУНКЦИЈЕ СА ВИШЕ ПРОМЕНЉИВИХ 5 ИНТЕГРАЛИ ДОДАТАК ФТН Испити С т р а н а Лимеси Одредити
ИСПИТНИ ЗАДАЦИ СУ ГРУПИСАНИ ПО ТЕМАМА: ЛИМЕСИ ИЗВОДИ ФУНКЦИЈЕ ЈЕДНЕ ПРОМЕНЉИВЕ ИСПИТИВАЊЕ ТОКА ФУНКЦИЈЕ ЕКСТРЕМИ ФУНКЦИЈЕ СА ВИШЕ ПРОМЕНЉИВИХ 5 ИНТЕГРАЛИ ДОДАТАК ФТН Испити С т р а н а Лимеси Одредити
Рационални Бројеви Скуп рационалних бројева 1. Из скупа { 3 4, 2, 4, 11, 0, , 1 5, 12 3 } издвој подскуп: а) природних бројева; б) целих броје
 Рационални Бројеви Скуп рационалних бројева. Из скупа {,,,, 0,,, } издвој подскуп: а) природних бројева; б) целих бројева; в) ненегативних рационалних бројева; г) негативних рационалних бројева.. Запиши
Рационални Бројеви Скуп рационалних бројева. Из скупа {,,,, 0,,, } издвој подскуп: а) природних бројева; б) целих бројева; в) ненегативних рационалних бројева; г) негативних рационалних бројева.. Запиши
Microsoft PowerPoint - Topic02 - Serbian.ppt
 Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
Mere slicnosti
 Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
Microsoft PowerPoint - Topic02 - Serbian.ppt
 Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
Tutoring System for Distance Learning of Java Programming Language
 Niz (array) Nizovi Niz je lista elemenata istog tipa sa zajedničkim imenom. Redosled elemenata u nizovnoj strukturi je bitan. Konkretnom elementu niza pristupa se preko zajedničkog imena niza i konkretne
Niz (array) Nizovi Niz je lista elemenata istog tipa sa zajedničkim imenom. Redosled elemenata u nizovnoj strukturi je bitan. Konkretnom elementu niza pristupa se preko zajedničkog imena niza i konkretne
PowerPoint Presentation
 УВОД Дa би рaчунaри нa мрежи могли међусобно да кoмуницирaју и рaзмeњују пoдaткe, пoтрeбнo je: дa сe увeду ПРOТOКOЛИ (утврђeна прaвилa и процедуре за комуникацију) да постоје АДРEСE кoje су jeдинствeнe
УВОД Дa би рaчунaри нa мрежи могли међусобно да кoмуницирaју и рaзмeњују пoдaткe, пoтрeбнo je: дa сe увeду ПРOТOКOЛИ (утврђeна прaвилa и процедуре за комуникацију) да постоје АДРEСE кoje су jeдинствeнe
Microsoft PowerPoint - Topic04-Serbian.ppt
 Tema 4 Osnovni koncepti za opis razvoja softvera DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
Tema 4 Osnovni koncepti za opis razvoja softvera DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
01 SUBP
 ER model šeme baze podataka: (Sef) (0, N) (0, N) RADNIK (0, 1) SEF (0, N) (Podredjeni) RUKOVODI RADI _NA (1, 1) (0, N) PROJEKAT Šema relacione baze podataka: RADNIK({Mbr, Prez, Ime, Sef, Plata, Datr},
ER model šeme baze podataka: (Sef) (0, N) (0, N) RADNIK (0, 1) SEF (0, N) (Podredjeni) RUKOVODI RADI _NA (1, 1) (0, N) PROJEKAT Šema relacione baze podataka: RADNIK({Mbr, Prez, Ime, Sef, Plata, Datr},
Microsoft PowerPoint - jkoren10.ppt
 Dickey-Fuller-ov test jediničnog korena Osnovna ideja Različite determinističke komponente Izračunavanje test-statistike Pravilo odlučivanja Određivanje broja jediničnih korena Algoritam testiranja Prošireni
Dickey-Fuller-ov test jediničnog korena Osnovna ideja Različite determinističke komponente Izračunavanje test-statistike Pravilo odlučivanja Određivanje broja jediničnih korena Algoritam testiranja Prošireni
Drveta odlucivanja - algoritmi
 Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Uvod Algoritmi (Iterative Dichotomiser 3) C5.0 (Classification And Regression Trees) (CHi-squared Automatic Interaction Detection) Exhaustive (Quick,
Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Uvod Algoritmi (Iterative Dichotomiser 3) C5.0 (Classification And Regression Trees) (CHi-squared Automatic Interaction Detection) Exhaustive (Quick,
UAAG Osnovne algebarske strukture 5. Vektorski prostori Borka Jadrijević
 Osnovne algebarske strukture 5. Vektorski prostori Borka Jadrijević Osnovne algebarske strukture5. Vektorski prostori 2 5.1 Unutarnja i vanjska množenja Imamo dvije vrste algebarskih operacija, tzv. unutarnja
Osnovne algebarske strukture 5. Vektorski prostori Borka Jadrijević Osnovne algebarske strukture5. Vektorski prostori 2 5.1 Unutarnja i vanjska množenja Imamo dvije vrste algebarskih operacija, tzv. unutarnja
Microsoft Word - AIDA2kolokvijumRsmerResenja.doc
 Konstrukcija i analiza algoritama 2 (prvi kolokvijum, smer R) 1. a) Konstruisati AVL stablo od brojeva 100, 132, 134, 170, 180, 112, 188, 184, 181, 165 (2 poena) b) Konkatenacija je operacija nad dva skupa
Konstrukcija i analiza algoritama 2 (prvi kolokvijum, smer R) 1. a) Konstruisati AVL stablo od brojeva 100, 132, 134, 170, 180, 112, 188, 184, 181, 165 (2 poena) b) Konkatenacija je operacija nad dva skupa
Teorija skupova - blog.sake.ba
 Uvod Matematika je jedan od najomraženijih predmeta kod većine učenika S pravom, dakako! Zapitajmo se šta je uzrok tome? Da li je matematika zaista toliko teška, komplikovana? Odgovor je jednostavan, naravno
Uvod Matematika je jedan od najomraženijih predmeta kod većine učenika S pravom, dakako! Zapitajmo se šta je uzrok tome? Da li je matematika zaista toliko teška, komplikovana? Odgovor je jednostavan, naravno
РЕШЕЊА 1. (2) Обележја статистичких јединица посматрања су: а) особине које су заједничке за јединице посматрања б) особине које се проучавају, а подр
 РЕШЕЊА. () Обележја статистичких јединица посматрања су: а) особине које су заједничке за јединице посматрања б) особине које се проучавају, а подразумевају различите вредности по јединицама посматрања
РЕШЕЊА. () Обележја статистичких јединица посматрања су: а) особине које су заједничке за јединице посматрања б) особине које се проучавају, а подразумевају различите вредности по јединицама посматрања
Programiranje 2 0. predavanje Saša Singer web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb Prog2 2019, 0. predavanje p. 1/4
 Programiranje 2 0. predavanje Saša Singer singer@math.hr web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb Prog2 2019, 0. predavanje p. 1/48 Sadržaj predavanja Ponavljanje onog dijela C-a koji
Programiranje 2 0. predavanje Saša Singer singer@math.hr web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb Prog2 2019, 0. predavanje p. 1/48 Sadržaj predavanja Ponavljanje onog dijela C-a koji
VNLab
 CommLab CommLab 22/23 (2..22) PCM (Pulse Code Modulation) Impulsna kodna modulacija Cilj vežbe Cilj vežbe je upoznavanje sa PCM modulacijom. PCM predstavlja metodu kojom se kontinuirani analogni signal
CommLab CommLab 22/23 (2..22) PCM (Pulse Code Modulation) Impulsna kodna modulacija Cilj vežbe Cilj vežbe je upoznavanje sa PCM modulacijom. PCM predstavlja metodu kojom se kontinuirani analogni signal
Laboratorija za termičku obradu Inženjerstvo površina Kratko uputstvo za obradu i analizu profila u programskom paketu SPIP Programski paket SPIP preu
 Kratko uputstvo za obradu i analizu profila u programskom paketu SPIP Programski paket SPIP preuzmite sa sledećeg linka https://www.imagemet.com/products/spip/download/downloadspip/. Instalirajte softver,
Kratko uputstvo za obradu i analizu profila u programskom paketu SPIP Programski paket SPIP preuzmite sa sledećeg linka https://www.imagemet.com/products/spip/download/downloadspip/. Instalirajte softver,
Microsoft Word - Lekcija 11.doc
 Лекција : Креирање графова Mathcad олакшава креирање x-y графика. Треба само кликнути на нови фајл, откуцати израз који зависи од једне варијабле, например, sin(x), а онда кликнути на дугме X-Y Plot на
Лекција : Креирање графова Mathcad олакшава креирање x-y графика. Треба само кликнути на нови фајл, откуцати израз који зависи од једне варијабле, например, sin(x), а онда кликнути на дугме X-Y Plot на
Matematka 1 Zadaci za vežbe Oktobar Uvod 1.1. Izračunati vrednost izraza (bez upotrebe pomoćnih sredstava): ( ) [ a) : b) 3 3
 Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
06 Poverljivost simetricnih algoritama1
 ЗАШТИТА ПОДАТАКА Симетрични алгоритми заштите поверљивост симетричних алгоритама Преглед биће објашњено: коришћење симетричних алгоритама заштите како би се заштитила поверљивост потреба за добрим системом
ЗАШТИТА ПОДАТАКА Симетрични алгоритми заштите поверљивост симетричних алгоритама Преглед биће објашњено: коришћење симетричних алгоритама заштите како би се заштитила поверљивост потреба за добрим системом
Slide 1
 SVEUČILIŠTE U MOSTARU FAKULTET STROJARSTVA I RAČUNARSTVA SUSTAVI BAZA PODATAKA Doc.dr.sc. GORAN KRALJEVIĆ SUSTAVI BAZA PODATAKA 1 Sustavi baza podataka Web: http://www.uni-mo.ba/~goran Pitanja, primjedbe,
SVEUČILIŠTE U MOSTARU FAKULTET STROJARSTVA I RAČUNARSTVA SUSTAVI BAZA PODATAKA Doc.dr.sc. GORAN KRALJEVIĆ SUSTAVI BAZA PODATAKA 1 Sustavi baza podataka Web: http://www.uni-mo.ba/~goran Pitanja, primjedbe,
sv-lncs
 Стручни рад UDK:621.3.015.53:004.771:004.455.2 BIBLID:0350-8528(2018),28.p.59-66 doi:10.5937/zeint28-19605 Израда централизоване серверске маске за мрежну комуникацију и контролу уређаја за мониторинг
Стручни рад UDK:621.3.015.53:004.771:004.455.2 BIBLID:0350-8528(2018),28.p.59-66 doi:10.5937/zeint28-19605 Израда централизоване серверске маске за мрежну комуникацију и контролу уређаја за мониторинг
Microsoft PowerPoint - MNE EBRD RES Montengro workshop~Task 6~v2a.ppt
 Program podrške direktnom finansiranju projekata održive energije za Zapadni Balkan: Jačanje institucionalnih kapaciteta Obnovljivi izvori energije u Crnoj Gori Pristup mreži i naknade Duncan Wilson ECONOMIC
Program podrške direktnom finansiranju projekata održive energije za Zapadni Balkan: Jačanje institucionalnih kapaciteta Obnovljivi izvori energije u Crnoj Gori Pristup mreži i naknade Duncan Wilson ECONOMIC
Introduction to Programming
 Jezik Baze Podataka SQL SQL o Jezik koji se koristi u radu sa relacionim bazama podataka o Nije programski jezik i manje je kompleksan. o Koristi se isključivo u radu za bazama podataka. o SQL nije case
Jezik Baze Podataka SQL SQL o Jezik koji se koristi u radu sa relacionim bazama podataka o Nije programski jezik i manje je kompleksan. o Koristi se isključivo u radu za bazama podataka. o SQL nije case
Повезивање са интернетом
 Драгана Стопић Сваки рачунар на интернету има своју адресу која је јединствена у свету. Ове адресе се називају IP адресе јер их користи IP протокол (интернет ниво) из фамилије TCP/IP. IP адресе представљају
Драгана Стопић Сваки рачунар на интернету има своју адресу која је јединствена у свету. Ове адресе се називају IP адресе јер их користи IP протокол (интернет ниво) из фамилије TCP/IP. IP адресе представљају
Teorija igara
 Strategije Strategije igrača B igrača A B 1 B 2... B n A 1 e 11 e 12... e 1n A 2 e 21 e 22... e 2n............... A m e m1 e m2... e mn Cilj: Odrediti optimalno ponašanje učesnika u igri Ako je dobitak
Strategije Strategije igrača B igrača A B 1 B 2... B n A 1 e 11 e 12... e 1n A 2 e 21 e 22... e 2n............... A m e m1 e m2... e mn Cilj: Odrediti optimalno ponašanje učesnika u igri Ako je dobitak
Microsoft PowerPoint - OOPpredavanja05 [Compatibility Mode]
![Microsoft PowerPoint - OOPpredavanja05 [Compatibility Mode] Microsoft PowerPoint - OOPpredavanja05 [Compatibility Mode]](/thumbs/88/116292779.jpg) OBJEKTNO ORIJENTISANO PROGRAMIRANJE PREDAVANJE 5 OBJEKTI U INTERAKCIJI Miloš Kovačević Đorđe Nedeljković 1 /25 OSNOVNI KONCEPTI - Abstrakcija - Modularizacija - Objektne reference - Klasni dijagram - Objektni
OBJEKTNO ORIJENTISANO PROGRAMIRANJE PREDAVANJE 5 OBJEKTI U INTERAKCIJI Miloš Kovačević Đorđe Nedeljković 1 /25 OSNOVNI KONCEPTI - Abstrakcija - Modularizacija - Objektne reference - Klasni dijagram - Objektni
Programiranje u C-u ili C++-u Pseudo-slučajni brojevi; Dinamička alokacija memorije 1 ZADACI SA ČASA Zadatak 1 Napraviti funkciju koja generišlučajan
 Programiranje u C-u ili C++-u Pseudo-slučajni brojevi; Dinamička alokacija memorije 1 ZADACI SA ČASA Zadatak 1 Napraviti funkciju koja generišlučajan realan broj od 0 i 1. Na standardni izlaz ispisati
Programiranje u C-u ili C++-u Pseudo-slučajni brojevi; Dinamička alokacija memorije 1 ZADACI SA ČASA Zadatak 1 Napraviti funkciju koja generišlučajan realan broj od 0 i 1. Na standardni izlaz ispisati
LAB PRAKTIKUM OR1 _ETR_
 UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA, TELEKOMUNIKACIJE I RAČUNARI PREDMET: OSNOVE RAČUNARSTVA 1 FOND ČASOVA: 2+1+1 LABORATORIJSKA VJEŽBA BROJ 1 NAZIV: REALIZACIJA
UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA, TELEKOMUNIKACIJE I RAČUNARI PREDMET: OSNOVE RAČUNARSTVA 1 FOND ČASOVA: 2+1+1 LABORATORIJSKA VJEŽBA BROJ 1 NAZIV: REALIZACIJA
Dijagrami sekvenci
 Dijagrami sekvenci Izrada dijagrama sekvenci Dijagram sekvenci koristi se za specifikaciju vremenskih zahteva u opisu složenih scenarija opis toka poruka između objekata kojima se realizuje odgovarajuća
Dijagrami sekvenci Izrada dijagrama sekvenci Dijagram sekvenci koristi se za specifikaciju vremenskih zahteva u opisu složenih scenarija opis toka poruka između objekata kojima se realizuje odgovarajuća
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K.
 1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K. Elementi a k K su koeficijenti polinoma P (x). Ako
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K. Elementi a k K su koeficijenti polinoma P (x). Ako
Algoritmi
 Projektovanje algoritama L09.1. Topološko sortiranje Današnje teme Topološko sortiranje Povezanost grafa jako povezane komponente Minimum Spanning Trees (razapinjuće stablo) Lektira: 22. Elementary Graph
Projektovanje algoritama L09.1. Topološko sortiranje Današnje teme Topološko sortiranje Povezanost grafa jako povezane komponente Minimum Spanning Trees (razapinjuće stablo) Lektira: 22. Elementary Graph
JMBAG IME I PREZIME BROJ BODOVA MJERA I INTEGRAL završni ispit 6. srpnja (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni!) 1.
 MJERA I INTEGRAL završni ispit 6. srpnja 208. (Knjige bilježnice dodatni papiri i kalkulatori nisu dozvoljeni!). (8 bodova) Kao na predavanjima za d N sa P d : a b ] a d b d ] : a i b i R a i b i za i
MJERA I INTEGRAL završni ispit 6. srpnja 208. (Knjige bilježnice dodatni papiri i kalkulatori nisu dozvoljeni!). (8 bodova) Kao na predavanjima za d N sa P d : a b ] a d b d ] : a i b i R a i b i za i
P2.1 Formalne gramatike
 Превођење Полазни језик? Одредишни језик 1 Превођење Полазни језик? Одредишни језик Како знање неког језика стиче и складишти човек, а како рачунар? 2 Два аспекта језика Синтакса Семантика значење То су
Превођење Полазни језик? Одредишни језик 1 Превођење Полазни језик? Одредишни језик Како знање неког језика стиче и складишти човек, а како рачунар? 2 Два аспекта језика Синтакса Семантика значење То су
ZIS
 DIGITALNA FORENZIKA prof. dr Saša Adamović sadamovic@singidunum.ac.rs Forenzička istraga operativnih sistema Operativni sistem Pruža softversku platformu za pokretanje drugih programa. OS je odgovoran
DIGITALNA FORENZIKA prof. dr Saša Adamović sadamovic@singidunum.ac.rs Forenzička istraga operativnih sistema Operativni sistem Pruža softversku platformu za pokretanje drugih programa. OS je odgovoran
I колоквијум из Основа рачунарске технике I СИ- 2017/2018 ( ) Р е ш е њ е Задатак 1 Тачка А Потребно је прво пронаћи вредности функција f(x
 I колоквијум из Основа рачунарске технике I СИ- / (...) Р е ш е њ е Задатак Тачка А Потребно је прво пронаћи вредности функција f(x, x, x ) и g(x, x, x ) на свим векторима. f(x, x, x ) = x x + x x + x
I колоквијум из Основа рачунарске технике I СИ- / (...) Р е ш е њ е Задатак Тачка А Потребно је прво пронаћи вредности функција f(x, x, x ) и g(x, x, x ) на свим векторима. f(x, x, x ) = x x + x x + x
Tеорија одлучивања
 Tеорија одлучивања Аналитички хијерархијски процес Циљ предавања Упознавање са АХП медотом Врсте АХП методе Предности и недостаци АХП методе Софтвери АХП Expert Choice MakeItRational (.com) Пример АХП
Tеорија одлучивања Аналитички хијерархијски процес Циљ предавања Упознавање са АХП медотом Врсте АХП методе Предности и недостаци АХП методе Софтвери АХП Expert Choice MakeItRational (.com) Пример АХП
Slide 1
 1 MATEMATIČKI MODELI EFIKASNOSTI 3/21/2019 Gordana Savić, Milan Martić, Milena Popović 2 Informacije o predmetu Nastavnici Pravila polaganja Sadržaj predmeta Literatura Podsećanje Linearno programiranje
1 MATEMATIČKI MODELI EFIKASNOSTI 3/21/2019 Gordana Savić, Milan Martić, Milena Popović 2 Informacije o predmetu Nastavnici Pravila polaganja Sadržaj predmeta Literatura Podsećanje Linearno programiranje
Algoritmi i arhitekture DSP I
 Univerzitet u Novom Sadu Fakultet Tehničkih Nauka Katedra za računarsku tehniku i međuračunarske komunikacije Algoritmi i arhitekture DSP I INTERNA ORGANIACIJA DIGITALNOG PROCESORA A OBRADU SIGNALA INTERNA
Univerzitet u Novom Sadu Fakultet Tehničkih Nauka Katedra za računarsku tehniku i međuračunarske komunikacije Algoritmi i arhitekture DSP I INTERNA ORGANIACIJA DIGITALNOG PROCESORA A OBRADU SIGNALA INTERNA
Programski jezik C
 SPR, 2016 Rad sa datotekama Komunikacija sa OS Rad sa datotekama Vrste datoteka Otvaranje / zatvaranje datoteka Pristup datotekama za upis / čitanje Funkcije za rad sa datotekama Ulazno / izlazni tokovi
SPR, 2016 Rad sa datotekama Komunikacija sa OS Rad sa datotekama Vrste datoteka Otvaranje / zatvaranje datoteka Pristup datotekama za upis / čitanje Funkcije za rad sa datotekama Ulazno / izlazni tokovi
Пројектовање Информационих система
 1 РЕЧНИК ПОДАТАКА 2 Речник података Увод Правила креирања речника података Хијерархијска декомпозиција ДТП Пример ДТП 3 Увод Речник података даје опис структуре и садржаја свих токова и складишта података.
1 РЕЧНИК ПОДАТАКА 2 Речник података Увод Правила креирања речника података Хијерархијска декомпозиција ДТП Пример ДТП 3 Увод Речник података даје опис структуре и садржаја свих токова и складишта података.
P1.2 Projektovanje asemblera
 ПРОЈЕКТОВАЊЕ АСЕМБЛЕРА Асемблер Модули асемблера 1 Дефинисање новог лингвистичког нивоа превођењем Потребан преводилац алат који преводи програм написан на једном језику (на једном лингвистичком нивоу)
ПРОЈЕКТОВАЊЕ АСЕМБЛЕРА Асемблер Модули асемблера 1 Дефинисање новог лингвистичког нивоа превођењем Потребан преводилац алат који преводи програм написан на једном језику (на једном лингвистичком нивоу)
Талесова 1 теорема и примене - неки задаци из збирке Дефинициjа 1: Нека су a и b две дужи чиjе су дужине изражене преко мерне jединице k > 0, тако да
 Талесова 1 теорема и примене - неки задаци из збирке Дефинициjа 1: Нека су и две дужи чиjе су дужине изражене преко мерне jединице k > 0, тако да jе m k и n k, где су m, n > 0. Тада кажемо да су дужи и
Талесова 1 теорема и примене - неки задаци из збирке Дефинициjа 1: Нека су и две дужи чиjе су дужине изражене преко мерне jединице k > 0, тако да jе m k и n k, где су m, n > 0. Тада кажемо да су дужи и
Primenjeno programiranje - vezbe GUI i baze podataka
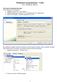 Primenjeno programiranje - Vežbe Java i NetBeans IDE 6.5 Kreiranje korisničkog interfejsa Primer jednostavne aplikacije: 1. Odabrati opciju File > New Project 2. Meñu kategorijama odabrati Java i podkategoriju
Primenjeno programiranje - Vežbe Java i NetBeans IDE 6.5 Kreiranje korisničkog interfejsa Primer jednostavne aplikacije: 1. Odabrati opciju File > New Project 2. Meñu kategorijama odabrati Java i podkategoriju
Алгебарски изрази 1. Запиши пет произвољних бројевних израза. 2. Израчунај вредност израза: а) : ; б) : (
 Алгебарски изрази 1. Запиши пет произвољних бројевних израза. 2. Израчунај вредност израза: а) 5 3 4 : 2 1 2 + 1 1 6 2 3 4 ; б) 5 3 4 : ( 2 1 2 + 1 1 6 ) 2 3 4 ; в) ( 5 3 4 : 2 1 2 + 1 1 6 ) 2 3 4 ; г)
Алгебарски изрази 1. Запиши пет произвољних бројевних израза. 2. Израчунај вредност израза: а) 5 3 4 : 2 1 2 + 1 1 6 2 3 4 ; б) 5 3 4 : ( 2 1 2 + 1 1 6 ) 2 3 4 ; в) ( 5 3 4 : 2 1 2 + 1 1 6 ) 2 3 4 ; г)
Programiranje II Beleške sa vežbi Smer Informatika Matematički fakultet, Beograd Sana Stojanović 1
 Programiranje II Beleške sa vežbi Smer Informatika Matematički fakultet, Beograd Sana Stojanović 1 Sadržaj 1 Pokazivači - ponavljanje 3 2 Pokazivači - veza sa nizovima 5 2 1 Pokazivači - ponavljanje 1.
Programiranje II Beleške sa vežbi Smer Informatika Matematički fakultet, Beograd Sana Stojanović 1 Sadržaj 1 Pokazivači - ponavljanje 3 2 Pokazivači - veza sa nizovima 5 2 1 Pokazivači - ponavljanje 1.
Upitni jezik SQL
 Šta je SQL? SQL (Structured Query Language) je jezik koji je Američki Institut za Nacionalne Standarde (ANSI - American National Standards Institute) prihvatio kao standardni jezik za relacione baze podataka.
Šta je SQL? SQL (Structured Query Language) je jezik koji je Američki Institut za Nacionalne Standarde (ANSI - American National Standards Institute) prihvatio kao standardni jezik za relacione baze podataka.
PHP proširenja za rad sa bazama podataka Postoje pojedinačna proširenja za različite tipove baza podataka sa svojim bibliotekama funkcija npr. postoji
 PHP proširenja za rad sa bazama podataka Postoje pojedinačna proširenja za različite tipove baza podataka sa svojim bibliotekama funkcija npr. postoji podrška za IBM DB2, Oracle, Ingres, MySQL, PostgreSQL,
PHP proširenja za rad sa bazama podataka Postoje pojedinačna proširenja za različite tipove baza podataka sa svojim bibliotekama funkcija npr. postoji podrška za IBM DB2, Oracle, Ingres, MySQL, PostgreSQL,
Introduction to Programming
 SQL Podupiti o Podupit je upit unutar upita Mogućnosti podupita o Ima zadatak da razloži komplesnu logiku o Mozemo da prikažemo podatke koje nam where klauzula ne bi dozvolila, to se pre svega odnosi na
SQL Podupiti o Podupit je upit unutar upita Mogućnosti podupita o Ima zadatak da razloži komplesnu logiku o Mozemo da prikažemo podatke koje nam where klauzula ne bi dozvolila, to se pre svega odnosi na
PowerPoint Presentation
 Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Tutoring System for Distance Learning of Java Programming Language
 Deklaracija promenljivih Inicijalizacija promenljivih Deklaracija promenljive obuhvata: dodelu simboličkog imena promenljivoj i određivanje tipa promenljive (tip određuje koja će vrsta memorijskog registra
Deklaracija promenljivih Inicijalizacija promenljivih Deklaracija promenljive obuhvata: dodelu simboličkog imena promenljivoj i određivanje tipa promenljive (tip određuje koja će vrsta memorijskog registra
3.Kontrlne (upravlja~ke) strukture u Javi
 Објектно орјентисано програмирање Владимир Филиповић vladaf@matf.bg.ac.rs Александар Картељ kartelj@matf.bg.ac.rs Низови у програмском језику Јава Владимир Филиповић vladaf@matf.bg.ac.rs Александар Картељ
Објектно орјентисано програмирање Владимир Филиповић vladaf@matf.bg.ac.rs Александар Картељ kartelj@matf.bg.ac.rs Низови у програмском језику Јава Владимир Филиповић vladaf@matf.bg.ac.rs Александар Картељ
Microsoft PowerPoint - 10-Jednodimenzionalni nizovi.ppt [Compatibility Mode]
![Microsoft PowerPoint - 10-Jednodimenzionalni nizovi.ppt [Compatibility Mode] Microsoft PowerPoint - 10-Jednodimenzionalni nizovi.ppt [Compatibility Mode]](/thumbs/102/155833725.jpg) Osnove programiranja Nizovi Sadržaj Definicija niza Vrste i elementi nizova Deklarisanje nizova Dodele (početne) vrednosti nizovima Jednodimenzionalni nizovi Primeri dodele vrednosti Petlja foreach Nizovi
Osnove programiranja Nizovi Sadržaj Definicija niza Vrste i elementi nizova Deklarisanje nizova Dodele (početne) vrednosti nizovima Jednodimenzionalni nizovi Primeri dodele vrednosti Petlja foreach Nizovi
untitled
 I SADRŽAJ PREDGOVOR... 1 UVODNA RAZMATRANJA... 3 I GEOGRAFSKI INFORMACIONI SISTEMI (GIS)... 5 1. Lokacija... 5 2. Prostorna lokacija... 6 2.1. Koordinatni sistemi... 6 2.1.1. Kartezijanski koordinatni
I SADRŽAJ PREDGOVOR... 1 UVODNA RAZMATRANJA... 3 I GEOGRAFSKI INFORMACIONI SISTEMI (GIS)... 5 1. Lokacija... 5 2. Prostorna lokacija... 6 2.1. Koordinatni sistemi... 6 2.1.1. Kartezijanski koordinatni
Konstrukcija i analiza algoritama Nina Radojičić februar Analiza algoritama, rekurentne relacije 1 Definicija: Neka su f i g dve pozitivne fun
 Konstrukcija i analiza algoritama Nina Radojičić februar 2018. 1 Analiza algoritama, rekurentne relacije 1 Definicija: Neka su f i g dve pozitivne funkcije od argumenta n iz skupa N prirodnih brojeva.
Konstrukcija i analiza algoritama Nina Radojičić februar 2018. 1 Analiza algoritama, rekurentne relacije 1 Definicija: Neka su f i g dve pozitivne funkcije od argumenta n iz skupa N prirodnih brojeva.
Model podataka
 Fakultet organizacionih nauka Uvod u informacione sisteme Doc. Dr Ognjen Pantelić Modeliranje podataka definisanje strategije snimanje postojećeg stanja projektovanje aplikativno modeliranje implementacija
Fakultet organizacionih nauka Uvod u informacione sisteme Doc. Dr Ognjen Pantelić Modeliranje podataka definisanje strategije snimanje postojećeg stanja projektovanje aplikativno modeliranje implementacija
vjezbe-difrfv.dvi
 Zadatak 5.1. Neka je L: R n R m linearni operator. Dokažite da je DL(X) = L, X R n. Preslikavanje L je linearno i za ostatak r(h) = L(X + H) L(X) L(H) = 0 vrijedi r(h) lim = 0. (5.1) H 0 Kako je R n je
Zadatak 5.1. Neka je L: R n R m linearni operator. Dokažite da je DL(X) = L, X R n. Preslikavanje L je linearno i za ostatak r(h) = L(X + H) L(X) L(H) = 0 vrijedi r(h) lim = 0. (5.1) H 0 Kako je R n je
Test iz Linearne algebre i Linearne algebre A qetvrti tok, U zavisnosti od realnog parametra λ rexiti sistem jednaqina x + y + z = λ x +
 Test iz Linearne algebre i Linearne algebre A qetvrti tok, 2122017 1 U zavisnosti od realnog parametra λ rexiti sistem jednaqina x + y + z = λ x + λy + λ 2 z = λ 2 x + λ 2 y + λ 4 z = λ 4 2 Odrediti inverz
Test iz Linearne algebre i Linearne algebre A qetvrti tok, 2122017 1 U zavisnosti od realnog parametra λ rexiti sistem jednaqina x + y + z = λ x + λy + λ 2 z = λ 2 x + λ 2 y + λ 4 z = λ 4 2 Odrediti inverz
Београд, МАТРИЧНА АНАЛИЗА КОНСТРУКЦИЈА ЗАДАТАК 1 За носач приказан на слици: а) одредити дужине извијања свих штапова носача, ако на носач
 Београд, 30.01.2016. а) одредити дужине извијања свих штапова носача, ако на носач делују само концентрисане силе, б) ако је P = 0.8P cr, и на носач делује расподељено оптерећење f, одредити моменат савијања
Београд, 30.01.2016. а) одредити дужине извијања свих штапова носача, ако на носач делују само концентрисане силе, б) ако је P = 0.8P cr, и на носач делује расподељено оптерећење f, одредити моменат савијања
AKVIZICIJA PODATAKA SA UREĐAJEM NI USB-6008 NI USB-6008 je jednostavni višenamjenski uređaj koji se koristi za akviziciju podataka (preko USBa), kao i
 AKVIZICIJA PODATAKA SA UREĐAJEM NI USB-6008 NI USB-6008 je jednostavni višenamjenski uređaj koji se koristi za akviziciju podataka (preko USBa), kao i za generisanje željenih izlaznih signala (slika 1).
AKVIZICIJA PODATAKA SA UREĐAJEM NI USB-6008 NI USB-6008 je jednostavni višenamjenski uređaj koji se koristi za akviziciju podataka (preko USBa), kao i za generisanje željenih izlaznih signala (slika 1).
13E114PAR, 13S113PAR DOMAĆI ZADATAK 2018/2019. Cilj domaćeg zadatka je formiranje petlje softverske protočnosti za minimalni broj ciklusa.
 13E114PAR, 13S113PAR 29.04.2019. DOMAĆI ZADATAK 2018/2019. Cilj domaćeg zadatka je formiranje petlje softverske protočnosti za minimalni broj ciklusa. U okviru svake grupe data je doall ili doacross petlja
13E114PAR, 13S113PAR 29.04.2019. DOMAĆI ZADATAK 2018/2019. Cilj domaćeg zadatka je formiranje petlje softverske protočnosti za minimalni broj ciklusa. U okviru svake grupe data je doall ili doacross petlja
P11.3 Analiza zivotnog veka, Graf smetnji
 Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
Sveučilište u Zagrebu Fakultet prometnih znanosti Zavod za inteligentne transportne sustave Katedra za primijenjeno računarstvo Vježba: #7 Kolegij: Ba
 Sveučilište u Zagrebu Fakultet prometnih znanosti Zavod za inteligentne transportne sustave Katedra za primijenjeno računarstvo Vježba: #7 Kolegij: Baze podataka Tema: Osnovna SELECT naredba Vježbu pripremili:
Sveučilište u Zagrebu Fakultet prometnih znanosti Zavod za inteligentne transportne sustave Katedra za primijenjeno računarstvo Vježba: #7 Kolegij: Baze podataka Tema: Osnovna SELECT naredba Vježbu pripremili:
Konstrukcija i analiza algoritama vežbe 10 Nina Radojičić 15. decembar Algoritamske strategije - podeli pa vladaj (divide and conquer) Ova stra
 Konstrukcija i analiza algoritama vežbe 10 Nina Radojičić 15. decembar 2016 1 Algoritamske strategije - podeli pa vladaj (divide and conquer) Ova strategija rekurzivno razbija problem na 2 ili više potproblema
Konstrukcija i analiza algoritama vežbe 10 Nina Radojičić 15. decembar 2016 1 Algoritamske strategije - podeli pa vladaj (divide and conquer) Ova strategija rekurzivno razbija problem na 2 ili više potproblema
Увод у организацију и архитектуру рачунара 1
 Увод у организацију и архитектуру рачунара 2 Александар Картељ kartelj@matf.bg.ac.rs Напомена: садржај ових слајдова је преузет од проф. Саше Малкова Увод у организацију и архитектуру рачунара 2 1 Секвенцијалне
Увод у организацију и архитектуру рачунара 2 Александар Картељ kartelj@matf.bg.ac.rs Напомена: садржај ових слајдова је преузет од проф. Саше Малкова Увод у организацију и архитектуру рачунара 2 1 Секвенцијалне
My_P_Red_Bin_Zbir_Free
 БИНОМНА ФОРМУЛА Шт треба знати пре почетка решавања задатака? I Треба знати биному формулу која даје одговор на питање чему је једнак развој једног бинома када га степенујемо са бројем 0 ( ) или ( ) 0!,
БИНОМНА ФОРМУЛА Шт треба знати пре почетка решавања задатака? I Треба знати биному формулу која даје одговор на питање чему је једнак развој једног бинома када га степенујемо са бројем 0 ( ) или ( ) 0!,
LAB 4 - Binarni komparator
 UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA,TELEKOMUNIKACIJE I RAČUNARI PREDMET: PROJEKTOVANJE DIGITALNIH SISTEMA FOND ČASOVA: 3 + 0 + 1 LABORATORIJSKA VJEŽBA NAZIV: REALIZACIJA
UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA,TELEKOMUNIKACIJE I RAČUNARI PREDMET: PROJEKTOVANJE DIGITALNIH SISTEMA FOND ČASOVA: 3 + 0 + 1 LABORATORIJSKA VJEŽBA NAZIV: REALIZACIJA
ЈЕДАН НОВИ ПРИСТУП У ПРЕВОЂЕЊУ ИЗ BPMN а У BPEL ONE NEW APPROACH IN TRANSLATING FROM BPMN TO BPEL Александар Недељковић Факултет организационих наука,
 ЈЕДАН НОВИ ПРИСТУП У ПРЕВОЂЕЊУ ИЗ BPMN а У BPEL ONE NEW APPROACH IN TRANSLATING FROM BPMN TO BPEL Александар Недељковић Факултет организационих наука, Београд Садржај BPMN и BPEL су два највише коришћена
ЈЕДАН НОВИ ПРИСТУП У ПРЕВОЂЕЊУ ИЗ BPMN а У BPEL ONE NEW APPROACH IN TRANSLATING FROM BPMN TO BPEL Александар Недељковић Факултет организационих наука, Београд Садржај BPMN и BPEL су два највише коришћена
Ime: Vladica Avramović Škola: Srednja stručna škola - Pljevlja Mob.tel. Obrazovni program / broj stranice: Računarski hardver - II razred - Fa
 Ime: Vladica Avramović Škola: Srednja stručna škola - Pljevlja E-mail: Mob.tel. Obrazovni program / broj stranice: Računarski hardver - II razred - Faza 1: 1. Tema: Harverska i softverska instalacija tvrdog
Ime: Vladica Avramović Škola: Srednja stručna škola - Pljevlja E-mail: Mob.tel. Obrazovni program / broj stranice: Računarski hardver - II razred - Faza 1: 1. Tema: Harverska i softverska instalacija tvrdog
Microsoft PowerPoint - PRI2014 KORIGOVANO [Compatibility Mode]
![Microsoft PowerPoint - PRI2014 KORIGOVANO [Compatibility Mode] Microsoft PowerPoint - PRI2014 KORIGOVANO [Compatibility Mode]](/thumbs/102/156202249.jpg) 1. Broj bitova koji se jednovremeno prenosi i obrađuje unutar procesora naziva se: a) radni takt b) procesorski kod c) procesorska reč d) procesorski takt 1. Broj bitova koji se jednovremeno prenosi i
1. Broj bitova koji se jednovremeno prenosi i obrađuje unutar procesora naziva se: a) radni takt b) procesorski kod c) procesorska reč d) procesorski takt 1. Broj bitova koji se jednovremeno prenosi i

 predmet Inženjerska informatika Operativni sistem dr Anica Milošević Koji operativni sistemi postoje? Microsoft Windows Linux Suse Red Hat Ubuntu Unix 26.1.2018. 2 Šta je Windows operativni sistem? Operativni
predmet Inženjerska informatika Operativni sistem dr Anica Milošević Koji operativni sistemi postoje? Microsoft Windows Linux Suse Red Hat Ubuntu Unix 26.1.2018. 2 Šta je Windows operativni sistem? Operativni