Microsoft Word Lj. Vasov.doc
|
|
|
- Вита Огњеновић
- пре 5 година
- Прикази:
Транскрипт
1 Docent dr Ljubiša Vasov, dipl. inž. Saobraćajni faultet, Beograd OCENA BEZOKAZNOG RADA VAZDUHOPLOVA UDC: Rezime: Pouzdanosao omplesni poazatelj valiteta funcionisanja sistema, zavisno od njegove osnovne namene i uslova procesa esploatacije, obuhvata različite arateristie sistema. Uzimajući u obzir specifične funcionalne zahteve vazduhoplova, oji se odnose, pre svega, na bezbednost leta, jedno od primarnih svojstava njihove pouzdanosti jeste bezoaznost. U ovom radu, razmatranjem arateristia stacionarnog procesa obnavljanja, ocenjena je verovatnoća bezoaznog rada vazduhoplova toom datog vremena trajanja leta i analizom funcije pouzdanosti utvrđene su donja i gornja granica verovatnoće bezoaznog rada. ime je poazana mogućnost pratične primene esponencijalne raspodele pri razmatranju bezoaznosti i priazan je način definisanja indiatora pouzdanosti vazduhoplova. Ključne reči: vazduhoplov, pouzdanost, bezoaznost, indiatori pouzdanosti. ESIMAION OF AIRCRAF FAILURE-FREE PERFORMANCE Summary: Reliability as complex indicator of system operation quality, in dependence on system basic purpose and conditions of exploitation process, involves different system characteristics. Regarding to the specific operational requirements of aircraft, mainly related to the flight safety, one of primary attributes of their reliability is failure-free performance. In this paper, by considering the stationary conditions characteristics of renewal process, estimation of probability for failure-free operation during a given flight time is done, and by analysis of reliability function, lower and upper limits of probability for failure-free operation are established. hereby, possibility for practical application of exponential distribution for failure-free performance consideration is shown, and method of aircraft reliability indicators determination is represented. Key words: aircraft, reliability, failure-free performance, reliability indicators. Uvod Savremena vazduhoplovna transportna sredstva, sa onstrutivnog i struturalnog aspeta, predstavljaju veoma složene tehniče sisteme specifične funcionalne namene, od ojih se zahteva veoma viso nivo pouzdanosti izvršenja zadaa. Posmatrano sa aspeta ocene pouzdanosti, osnovne arateristie procesa esploatacije vazduhoplova mogu se formulisati na sledeći način: pri razmatranju problematie pouzdanosti vazduhoplov se može posmatrati ao obnovljiv sistem raovremenog dejstva, odnosno sa raim intervalom vremena ispunjavanja zadaa u odnosu na alendarso vreme esploatacije; jedno od osnovnih svojstava pouzdanosti vazduhoplova jeste njegova VOJNOEHNI^KI GLASNIK 2/
2 bezoaznost, oja se vantitativno ocenjuje verovatnoćom bezoaznog rada vazduhoplova toom intervala orišćenja, odnosno trajanja leta; posmatrano roz vremensu sliu procesa esploatacije, vreme obnavljanja vazduhoplova je rao u poređenju sa vremenom njegovog bezoaznog rada, čime oeficijent gotovosti ne utiče bitno na nivo efetivnosti sistema. Efetivnost tavog sistema, u osnovi, zavisi od broja oaza toom datog perioda esploatacije, odnosno od bezoaznosti oja je izražena srednjim vremenom rada do oaza. Preduslovi za ostvarivanje prethodno navedenih arateristia jesu izrazito viso nivo pogodnosti održavanja i preventivni arater procesa održavanja vazduhoplova, ojim se obezbeđuje potpuno obnavljanje radne sposobnosti omponenti i sistema. Pri tome, izbor i analiza riterijuma efetivnosti određene omponente ili sistema vazduhoplova obično se vrši na osnovu uticaja oaza date omponente na bezbednost leta, i uupnih posledica događaja oji su izazvani njenom nepouzdanošću. Ocena verovatnoće bezoaznog rada vazduhoplova Vazduhoplov se može posmatrati ao obnovljiv sistem, čija se bezoaznost ocenjuje verovatnoćom bezoaznog rada toom vremena ispunjavanja letnog zadaa ( ) od trenua (τ), odnosno u intervalu vremena orišćenja sistema (τ, τ + ). Matematiči model ojim se opisuje proces obnavljanja vazduhoplova pri oceni bezoaznosti uljučuje sledeće pretpostave [1]: vreme potrebno za obnavljanje radne sposobnosti vazduhoplova može se izuzeti iz dalje analize, u ojoj se vremensi fator ne razmatra preo alendarsog vremena već preo naleta aviona, čime se posmatrani proces svodi na obnavljanje sa trenutnim vremenom obnavljanja. Ovaav slučaj je često zastupljen u prasi, jer od najvećeg broja tehničih sistema jedinica vremena rada sistema i jedinica vremena obnavljanja su različite [2]; intervali naleta vazduhoplova između oaza predstavljaju međusobno nezavisne slučajne veličine; posle obnavljanja vazduhoplov poseduje ista svojstva ao i pre oaza, odnosno zaon raspodele verovatnoće naleta do oaza ne zavisi od broja oaza. Momenti obnavljanja (τ 1, τ 2, τ 3,..., τ n ) formiraju taav niz događaja oji nastaju jedan za drugim (sl. 1) u momentima vremena slučajno raspoređenim u posmatranom periodu, odnosno obrazuju slučajan to događaja oji se naziva procesom obnavljanja [1]. t 1 t 2 t 3 t n t n+1 τ 0 τ 1 τ 2 τ 3 τ n τ τ + τ n+1 θ Sl. 1 Grafion toa događaja uprocesu obnavljanja 134 VOJNOEHNI^KI GLASNIK 2/2007.
3 Od početnog trenua (τ 0 ) posle naleta (t 1 ) vazduhoplova u trenuu (τ 1 ) dešava se prvi oaz, pri čemu, prema prethodno usvojenim pretpostavama, u istom momentu dolazi do obnavljanja radne sposobnosti vazduhoplova. Posle naleta (t 2 ) ponovo dolazi do oaza u trenuu (τ 2 ) i istovremeno do njegovog obnavljanja, itd. Sup momenata obnavljanja obrazuje proces obnavljanja sistema, pri čemu se u posmatranom slučaju potoci pojave oaza i obnavljanja međusobno podudaraju. Bezoaznost vazduhoplova u datom procesu određena je verovatnoćom da toom vremena ( ) orišćenja (leta) od trenua (τ) u intervalu (τ, τ + ), neće doći do pojave oaza. Prema usvojenim oznaama (sl. 1), tražena verovatnoća bezoaznog rada R(τ, τ + ) može se izraziti u sledećem obliu, oji uljučuje sve moguće ishode [1]: gde je: h(x) gustina obnavljanja. Posle veliog broja događaja, opisani proces obnavljanja postaje približno stacionaran, pri čemu je opravdano oristiti relacije asimptotsog procesa u ojem zaon raspodele vremena bezoaznog rada vazduhoplova ne zavisi od naleta već samo od trajanja leta [3]: 1 R( t ) = lim R( τ,τ +t ) = τ R(x)dx = (3) 1 = [ 1 F(x)] dx gde je: srednje vreme bezoaznog rada. Ispitivanje oblia funcije R( ) moguće je izvršiti određivanjem prvog i drugog izvoda na osnovu prethodne relacije (3), za oje se dobijaju sledeći izrazi: R(τ,τ +t ) = P(t <θ)= = P( τ < τ;τ +t > τ +t ) n= 0 n n n+ 1 (1) 2 dr( t ) 1 F( ) d R( ) f ( ) = ; = 0 2 d d (4) Uolio do momenta (τ) nije bilo oaza (n = 0), tada se gornji uslovi bezoaznog rada mogu izraziti nejednačinom: τ 1 >τ +. Uvođenjem promenljive (x) umesto (τ n ), dobija se: x + t n+1 τ + t n+1 τ + x, čime se jednačina (1) verovatnoće bezoaznog rada u datom intervalu (τ, τ + ), za nestacionarni poto obnavljanja može priazati u obliu [3]: R(τ,τ +t ) = R(τ +t )+ τ + R(τ +t x) h(x)dx 0 (2) Vrednost drugog izvoda uazuje na to da funcija R( ) ima onvesan obli u odnosu na pravac vremense (t) ose, odnosno funcija R( ) nalazi se iznad tangente u tači ( ) i samim tim iznad tangente u tači ( = 0). Koeficijent pravca tangente na rivu funcije R( ) u tači ( = 0), prema (4), jedna je: R(t = 0) = 1, čime je jednačina ove tangente data u obliu: R(t ) = 1. Dobijena jednačina tangente uazuje na veoma važnu ocenu donje granice vrednosti verovatnoće bezoaznog rada R( ): VOJNOEHNI^KI GLASNIK 2/
4 R( ) 1 (5) Gornja granica vrednosti pomenute funcije R( ) određena je na osnovu opšte relacije funcije pouzdanosti, za početa intervala (τ,τ + ), gde je λ( ) intenzitet oaza na intervalu (θ): λ( ) d 0 λ(0) R( ) = e e (6) Primenom relacije za intenzitet oaza i prema jednačinama (3) i (4), može se napisati: 1 λ( ) = R( t dr( t ) dt ) = [ 1 F( x) ] 1 F( t ) dx pri čemu se na počeu intervala (τ,τ + ) za ( = 0), prema prethodnoj relaciji, dobija: 1 1 λ (0) = = (7) dx 0 [ 1 F( x) ] Za većinu modela promene intenziteta oaza može se zaljučiti da funcija intenziteta oaza obično ne zavisi od vremena ili ima monotono rastući arater sa malim gradijentom, čime je potvrđena nejednačina (6). ime je, prema jednačini (7), određena gornja granica vrednosti verovatnoće bezoaznog rada R( ): R( t ) e (8) Prethodno datim nejednačinama (5) i (8) dobijena je dvostrana ocena verovatnoće bezoaznog rada vazduhoplova, čija se vrednost nalazi između tangente u tači ( = 0) i esponencijalne funcije: 1 R( ) e (9) Približna vrednost verovatnoće bezoaznog rada Na osnovu malog broja pojava oaza, ao reih događaja oji se mogu javiti toom određenog intervala esploatacije vazduhoplova i dovesti do gubia njegove radne sposobnosti, moguća je samo približna ocena parametara pouzdanosti. Određivanje zaonitosti raspodele verovatnoće bezoaznog vremena rada u razmatranom slučaju je pratično veoma tešo, čime dvostrana ocena tražene verovatnoće u inženjersim proračunima i procenama dobija velii značaj. Razvijanjem esponencijalne funcije u red, nejednačina (9) može se napisati u obliu: 1 1 R(t ) 1 + 1! ! 3! (10) ime je dobijena približna relacija za verovatnoću bezoaznog rada u obliu: R( ) 1 (11) čijom primenom se pravi greša (δ), oja ne prelazi vrednost: δ< t VOJNOEHNI^KI GLASNIK 2/2007.
5 Odnos vrednosti vremena orišćenja (trajanja leta) vazduhoplova ( ) sa srednjim vremenom između oaza (), oja su arateristična za savremena vazduhoplovna prevozna sredstva, uazuje na to da donja i gornja granica (9) ocene tražene funcije verovatnoće bezoaznog rada obrazuju vrlo usu oblast mogućih vrednosti. Drugim rečima, ada je esponent u funciji (8) približan ili manji od vrednosti (0,01) donja i gornja granica se pratično polapaju [4], i može se oristiti aprosimacija preo srednjeg vremena između oaza (MBF Mean ime Between Failure): R(t ) = e 1 F(t ) MBF MBF MBF (12) Pri analizi bezoaznosti i bezbednosti vazduhoplova uglavnom se radi sa veoma malim intenzitetima oaza i relativno raim intervalima orišćenja, čime je primena date metode određivanja R( ) i F( ) opravdana. Priazana ocena verovatnoće bezoaznog rada vazduhoplova pratično je svedena na primenu esponencijalne raspodele, oja se zbog svojstva odsustva posledica teorijsi tačno ostvaruje za sisteme u ojima nema procesa trošenja toom vremena. Međutim, esponencijalnu raspodelu je opravdano oristiti od svih složenih sistema oji se sastoje od veliog broja visoo pouzdanih elemenata [5], u ojima procesi trošenja i starenja protiču sporo i mogu se zanemariti u relativno raim intervalima orišćenja [1], posebno uolio je izražen uticaj profilatičog aratera održavanja, ao što je to slučaj sa vazduhoplovima. reba naglasiti da se prema dosadašnjim isustvima, stečenim na održavanju različitih mehaničih i eletronsih sistema, u prasi može javiti uupno šest različitih modela [6] promene intenziteta oaza toom vea trajanja sistema (sl. 2). Model (A) jeste lasičan model, poznat pod nazivom riva ade, oji sadrži soro sva arateristična područja promene intenziteta oaza toom vea trajanja sistema, prisutna u većini ostalih modela. Model (B) arateriše se soro onstantnim ili polao rastućim intenzitetom oaza na počeu esploatacije, a zatim završava povećanim intenzitetom usled istrošenosti i starenja, slično ao u modelu (A). Prema modelu (C) celoupni ve trajanja sistema je praćen laganim A D B E C F Sl. 2 Postojeći modeli promene intenziteta oaza toom vea trajanja sistema VOJNOEHNI^KI GLASNIK 2/
6 i postepenim povećanjem intenziteta oaza, oje nema posebno izražene intervale nagle promene gradijenta. Model (D) priazuje niza nivo intenziteta oaza sistema na počeu esploatacije, ada je sistem nov ili malo orišćen, oji postepeno raste do nee približno onstantne vrednosti. Model (E) ima približno onstantan nivo intenziteta oaza toom vea trajanja, što je tipična osobina slučajnih oaza. Model (F) počinje povećanim intenzitetom oaza sistema, slično modelu (A), oji se postepeno smanjuje do neog približno onstantnog ili blago rastućeg nivoa. Primera radi, istraživanja sprovedena na civilnim vazduhoplovima uazuju da se prema modelu (A) ponaša 4% omponenti, prema modelu (B) do 2%, modelu (C) oo 5%, prema modelu (D) do 7% omponenti, modelu (E) približno 14% i modelu (F) ne više od 68%. Ovava raspodela pojedinih oblia ponašanja sistema toom vea trajanja nije ista za druge vidove tehničih sistema. Međutim, može se uočiti opšta tendencija da sa povećanjem složenosti sistema sve veći doprinos pripada modelima (E) i (F). ime se, na osnovu modela promene intenziteta oaza (sl. 2), može uočiti da toom esploatacije najveći deo vremena pripada periodu sa približno onstantnim ili blago rastućim intenzitetom oaza, odnosno za dati interval može se usvojiti: λ(t) const. Koeficijenti pouzdanosti vazduhoplova Pri određivanju poazatelja pouzdanosti omponenti i sistema vazduhoplova početni ulazni podaci jesu uupno radno opterećenje razmatranog supa omponenti i uupan broj događaja (oaza) oji su vezani za dati sup i interesantni za pouzdanost, u posmatranom alendarsom periodu esploatacije. Jedan od osnovnih statističih poazatelja pouzdanosti jeste srednje vreme rada (j) po j-tom događaju: n t i i= j = 1 (13) N j gde je: n uupan broj omponenti u razmatranom supu (floti aviona), t i vreme rada i-te omponente u datom alendarsom periodu, i Nj broj j-tih događaja interesantnih za pouzdanost, u posmatranom periodu. Značenje srednjeg vremena (j) prema izrazu (13) približava se matematičom očeivanju vremena rada do pojave datog događaja, oje arateriše dati sup, samo pri analizi velie grupe istih omponenti. Prethodna činjenica uazuje na to da vreme (j) predstavlja srednju arateristiu pouzdanosti omponenti i sistema, sa različitim stepenima odrađenog resursa. Međutim, u mnogim pratičnim zadacima veličina (j) u potpunosti određuje poto događaja interesantnih za pouzdanost, oji su vezani za dati tip omponenti i mogu se tretirati ao obli oaza posmatrane omponente. Pomenuti način vantifiacije pouzdanosti, za određeni alendarsi period, često se u prasi realizuje preo odgovarajućih oeficijenata pouzdanosti (Kj), oji priazuju broj j-tih događaja oji, u stvari, predstavljaju ispoljavanje nepouzdanosti omponente toom procesa es- 138 VOJNOEHNI^KI GLASNIK 2/2007.
7 ploatacije, na 1000 odgovarajućih jedinica rada date omponente: K j 1000 = (14) j Smanjenje oeficijenta razmatranih događaja, datog prema prethodnoj relaciji (14), arateriše povećanje pouzdanosti omponente ili sistema, i obično se oristi promena (Kj) i (j) toom alendarsog vremena esploatacije, pri analizi dinamie promene pouzdanosti omponente. Priazani jednostavni statističi poazatelji omogućavaju rešavanje različitih zadataa povezanih sa problematiom određivanja verovatnoće ispunjavanja funcije cilja i ocene efetivnosti sistema vazduhoplova. reba napomenuti da se vantifiacija pouzdanosti u sličnom obliu, preo srednjeg ili godišnjeg intenziteta oaza (Average or Annual Failure Rate AFR), primenjuje i od drugih tipova tehničih sistema [7] [8]. Zaljuča Viso nivo pouzdanosti današnjih vazduhoplovnih prevoznih sredstava i činjenica da oazi oji dovode do gubia radne sposobnosti vazduhoplova predstavljaju ree događaje, uazuju na to da određivanje zaona raspodele vremena leta aviona do oaza predstavlja veoma teža zadata. ime dvostrana ocena funcije verovatnoće bezoaznog rada može imati velii značaj. Priazanom analizom funcije pouzdanosti i utvrđivanjem donje i gornje granice verovatnoće bezoaznog rada poazana je mogućnost pratične primene esponencijalne raspodele pri razmatranju bezoaznosti. Pored toga, dato je pratično značenje statističih poazatelja, oji se odnose na arateristične događaje vezane za pouzdanost i prate toom esploatacije vazduhoplova. Uobičajena prasa praćenja pouzdanosti flote, od većine vazduhoplovnih ompanija, sastoji se u sistematsom registrovanju podataa bitnih za pouzdanost, oji se obično priazuju u obliu mesečnih, polugodišnjih i godišnjih izveštaja. Sadržaj pomenutih podataa obuhvata događaje, ao što su: primedbe pilota i mehaničara, tehniči incidenti i ašnjenja, prevremena sidanja omponenti sa aviona, potvrđeni varovi, gašenje motora u letu, itd. Na osnovu broja registrovanih događaja u posmatranom alendarsom periodu i uupnog naleta flote aviona datog tipa u istom periodu, vrši se izračunavanje i praćenje onretnih indiatora (oeficijenata) pouzdanosti. Jedan od zadataa praćenja indiatora pouzdanosti jeste analiza trendova promene i registrovanje odstupanja stopa dešavanja događaja interesantnih za ocenu pouzdanosti flote, od normiranih vrednosti. Dobijeni izvorni podaci, ao omponente vremense serije oja obično obuhvata mali broj događaja, u reim slučajevima omogućavaju neposredan grafiči priaz pogodan za dalju analizu trendova promene. Veoma često, empirijsi podaci imaju viso stepen rasturanja vrednosti, ombinovan sa određenim periodičnim modelom promene, oji, uglavnom, zavisi od sezonse promene dinamie orišćenja flote. Radi smanjenja stepena rasturanja i ublažavanja na- VOJNOEHNI^KI GLASNIK 2/
8 glih slučajnih promena vrednosti indiatora pouzdanosti, pri izračunavanju datih indiatora obično se u prasi oristi metoda poretnih sredina. Literatura: [1] Анцелиович, Л. Л.: Надежность, безопасность и живучесть самолëта, Машиностроение, Москва, [2] Knežević, J.: Osnove teorije obnavljanja, Održavanje Mašina i Opreme OMO XXIV, Novinso-izdavača radna organizacija OMO, Beograd, broj 6 7, 1995, pp [3] Половко, А. М., Маликов, И. М., Жигарев, В. И., Зарудный, В. И.: Сборник задач по теории надежности, Советское радио, Москва, [4] raining Program for Reliability Probability and Safety Analysis, Volume I-II-III-IV, Prepared for the Federal Aviation Administration Under Contract No. DO FA75AC- 5123, Douglas Aircraft Company, August, [5] Смирнов, Н. Н., Андронов, А. М., Владиморов, А. М., Лемин Ю. И.: Эксплуатационная недежность и режимы технического обслуживания самолëтов, Транспорт, Москва, [6] Mourbay, J.: Reliability Centered Maintenance, Butterworth Heinemann, Oxford, Second edition, [7] Allmen, C. R., Lu M. W.: Sample size for Failure Detection and Reliability Demonstration, Proceedings Annual Reliability and Maintainability Symposium, IEEE Reliability Society, Atlanta, Georgia USA, January 26 28, 1993, pp [8] Elerath, J. G.: AFR: Problems of Definition, Calculation and Measurement in a Commercial Environment, Proceedings Annual Reliability and Maintainability Symposium, IEEE Reliability Society, Los Angeles, California USA, January 24 27, 2000, pp VOJNOEHNI^KI GLASNIK 2/2007.
Vjezbe 1.dvi
 Matematia I Elvis Baraović 0 listopada 08 Prirodno-matematiči faultet Univerziteta u Tuzli, Odsje matematia, Univerzitetsa 75000 Tuzla;http://pmfuntzba/staff/elvisbaraovic/ Sadržaj Sup realnih brojeva
Matematia I Elvis Baraović 0 listopada 08 Prirodno-matematiči faultet Univerziteta u Tuzli, Odsje matematia, Univerzitetsa 75000 Tuzla;http://pmfuntzba/staff/elvisbaraovic/ Sadržaj Sup realnih brojeva
ТЕОРИЈА УЗОРАКА 2
 ТЕОРИЈА УЗОРАКА 2 12. 04. 13. ВЕЖБАЊА Написати функције за бирање елемената популације обима N у узорак обима n, код простог случајног узорка, користећи алгоритме: Draw by draw procedure for SRS/SRSWOR
ТЕОРИЈА УЗОРАКА 2 12. 04. 13. ВЕЖБАЊА Написати функције за бирање елемената популације обима N у узорак обима n, код простог случајног узорка, користећи алгоритме: Draw by draw procedure for SRS/SRSWOR
Slide 1
 Statistička analiza u hidrologiji Uvod Statistička analiza se primenjuje na podatke osmatranja hidroloških veličina (najčešće: protoka i kiša) Cilj: opisivanje veze između veličine i verovatnoće njene
Statistička analiza u hidrologiji Uvod Statistička analiza se primenjuje na podatke osmatranja hidroloških veličina (najčešće: protoka i kiša) Cilj: opisivanje veze između veličine i verovatnoće njene
PI1_-_funkcije_i_srednja_log._temp._razlika
 lternativni način određivanja značaji istosjernog i protusjernog reuperatora U zadnje izdanju, ao i u prethodni izdanjia, udžbenia Terodinaia II, [], dano je analitičo rješenje značaji o ovisnosti o značajaa
lternativni način određivanja značaji istosjernog i protusjernog reuperatora U zadnje izdanju, ao i u prethodni izdanjia, udžbenia Terodinaia II, [], dano je analitičo rješenje značaji o ovisnosti o značajaa
Microsoft Word - TAcKA i PRAVA3.godina.doc
 TAČKA i PRAVA Najpre ćemo se upoznati sa osnovnim formulama i njihovom primenom.. Rastojanje izmeñu dve tače Ao su nam date tače A( x, y i B( x, y, onda rastojanje izmeñu njih računamo po formuli d( A,
TAČKA i PRAVA Najpre ćemo se upoznati sa osnovnim formulama i njihovom primenom.. Rastojanje izmeñu dve tače Ao su nam date tače A( x, y i B( x, y, onda rastojanje izmeñu njih računamo po formuli d( A,
PowerPoint Presentation
 Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Sa stanovišta pristupa problemu korišćenja kapaciteta, razlikuju se metode
Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Sa stanovišta pristupa problemu korišćenja kapaciteta, razlikuju se metode
Microsoft Word - 13pavliskova
 ПОДЗЕМНИ РАДОВИ 4 (5) 75-8 UDK 6 РУДАРСКО-ГЕОЛОШКИ ФАКУЛТЕТ БЕОГРАД YU ISSN 5494 ИЗВОД Стручни рад УПОТРЕБА ОДВОЈЕНОГ МОДЕЛА РЕГЕНЕРАЦИЈЕ ЗА ОДРЕЂИВАЊЕ ПОУЗДАНОСТИ ТРАНСПОРТНЕ ТРАКЕ Павлисковá Анна, Марасовá
ПОДЗЕМНИ РАДОВИ 4 (5) 75-8 UDK 6 РУДАРСКО-ГЕОЛОШКИ ФАКУЛТЕТ БЕОГРАД YU ISSN 5494 ИЗВОД Стручни рад УПОТРЕБА ОДВОЈЕНОГ МОДЕЛА РЕГЕНЕРАЦИЈЕ ЗА ОДРЕЂИВАЊЕ ПОУЗДАНОСТИ ТРАНСПОРТНЕ ТРАКЕ Павлисковá Анна, Марасовá
Paper Title (use style: paper title)
 Статистичка анализа коришћења електричне енергије која за последицу има примену повољнијег тарифног става Аутор: Марко Пантовић Факултет техничких наука, Чачак ИАС Техника и информатика, 08/09 e-mal адреса:
Статистичка анализа коришћења електричне енергије која за последицу има примену повољнијег тарифног става Аутор: Марко Пантовић Факултет техничких наука, Чачак ИАС Техника и информатика, 08/09 e-mal адреса:
MAZALICA DUŠKA.pdf
 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ELEKTROTEHNIČKI FAKULTET Sveučilišni studij OPTIMIRANJE INTEGRACIJE MALIH ELEKTRANA U DISTRIBUCIJSKU MREŽU Diplomski rad Duška Mazalica Osijek, 2014. SADRŽAJ
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ELEKTROTEHNIČKI FAKULTET Sveučilišni studij OPTIMIRANJE INTEGRACIJE MALIH ELEKTRANA U DISTRIBUCIJSKU MREŽU Diplomski rad Duška Mazalica Osijek, 2014. SADRŽAJ
FTN Novi Sad Katedra za motore i vozila Potrošnja goriva Teorija kretanja drumskih vozila Potrošnja goriva
 Ključni faktori: 1. ENERGIJA potrebna za kretanje vozila na određenoj deonici puta Povećanje E K pri ubrzavanju, pri penjanju, kompenzacija energetskih gubitaka usled dejstva F f i F W Zavisi od parametara
Ključni faktori: 1. ENERGIJA potrebna za kretanje vozila na određenoj deonici puta Povećanje E K pri ubrzavanju, pri penjanju, kompenzacija energetskih gubitaka usled dejstva F f i F W Zavisi od parametara
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K.
 1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K. Elementi a k K su koeficijenti polinoma P (x). Ako
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K. Elementi a k K su koeficijenti polinoma P (x). Ako
Slide 1
 Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
Slide 1
 Merni sistemi u računarstvu, http://automatika.etf.rs/sr/13e053msr Merna nesigurnost tipa A doc. dr Nadica Miljković, kabinet 68, nadica.miljkovic@etf.rs Prezentacija za ovo predavanje je skoro u potpunosti
Merni sistemi u računarstvu, http://automatika.etf.rs/sr/13e053msr Merna nesigurnost tipa A doc. dr Nadica Miljković, kabinet 68, nadica.miljkovic@etf.rs Prezentacija za ovo predavanje je skoro u potpunosti
Matematka 1 Zadaci za vežbe Oktobar Uvod 1.1. Izračunati vrednost izraza (bez upotrebe pomoćnih sredstava): ( ) [ a) : b) 3 3
 Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
18 1 DERIVACIJA 1.3 Derivacije višeg reda n-tu derivaciju funkcije f označavamo s f (n) ili u Leibnizovoj notaciji s dn y d x n. Zadatak 1.22 Nadite f
 8 DERIVACIJA.3 Derivacije višeg reda n-tu derivaciju funcije f označavamo s f (n) ili u Leibnizovoj notaciji s dn y d x n. Zadata. Nadite f (x) ao je (a) f(x) = ( + x ) arctg x (b) f(x) = e x cos x (a)
8 DERIVACIJA.3 Derivacije višeg reda n-tu derivaciju funcije f označavamo s f (n) ili u Leibnizovoj notaciji s dn y d x n. Zadata. Nadite f (x) ao je (a) f(x) = ( + x ) arctg x (b) f(x) = e x cos x (a)
ЗАДАЦИ ИЗ МАТЕМАТИКЕ ЗА ПРИПРЕМАЊЕ ЗАВРШНОГ ИСПИТА
 ЗАДАЦИ ИЗ МАТЕМАТИКЕ ЗА ПРИПРЕМАЊЕ ЗАВРШНОГ ИСПИТА p m m m Дат је полином ) Oдредити параметар m тако да полином p буде дељив са б) Одредити параметар m тако да остатак при дељењу p са буде једнак 7 а)
ЗАДАЦИ ИЗ МАТЕМАТИКЕ ЗА ПРИПРЕМАЊЕ ЗАВРШНОГ ИСПИТА p m m m Дат је полином ) Oдредити параметар m тако да полином p буде дељив са б) Одредити параметар m тако да остатак при дељењу p са буде једнак 7 а)
PRIRODNO-MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA MATEMATIKU I INFORMATIKU ZADACI SA REŠENJIMA SA PRIJEMNOG ISPITA IZ MATEMATIKE, JUN Odrediti
 PRIRODNO-MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA MATEMATIKU I INFORMATIKU ZADACI SA REŠENJIMA SA PRIJEMNOG ISPITA IZ MATEMATIKE, JUN 0. Odrediti moduo kompleksnog broja Rešenje: Uočimo da važi z = + i00
PRIRODNO-MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA MATEMATIKU I INFORMATIKU ZADACI SA REŠENJIMA SA PRIJEMNOG ISPITA IZ MATEMATIKE, JUN 0. Odrediti moduo kompleksnog broja Rešenje: Uočimo da važi z = + i00
Microsoft Word - 03_Stojkovic
 Eng. Rev. 30- (00) 7-36 7 UDK 6.37.54:6.39.8 OPTIMIZIRANI OTA-C NP FILTRI DRUGOG I ČETVRTOG REDA OPTIMIZED SECOND AND FOURTH-ORDER OTA-C LP FILTERS Nino STOJKOVIĆ Filip TOMLJENOVIĆ Saša VLAHINIĆ Sažeta:
Eng. Rev. 30- (00) 7-36 7 UDK 6.37.54:6.39.8 OPTIMIZIRANI OTA-C NP FILTRI DRUGOG I ČETVRTOG REDA OPTIMIZED SECOND AND FOURTH-ORDER OTA-C LP FILTERS Nino STOJKOVIĆ Filip TOMLJENOVIĆ Saša VLAHINIĆ Sažeta:
P1.1 Analiza efikasnosti algoritama 1
 Analiza efikasnosti algoritama I Asimptotske notacije Master metoda (teorema) 1 Asimptotske notacije (1/2) Služe za opis vremena izvršenja algoritma T(n) gde je n N veličina ulaznih podataka npr. br. elemenata
Analiza efikasnosti algoritama I Asimptotske notacije Master metoda (teorema) 1 Asimptotske notacije (1/2) Služe za opis vremena izvršenja algoritma T(n) gde je n N veličina ulaznih podataka npr. br. elemenata
Projektovanje tehnoloških procesa
 ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА Департман за производно машинство Пројектовање технолошких процеса Тема: Др Мијодраг Милошевић Технолошки процеси израде производа Део производног процеса у коме се врши измена
ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА Департман за производно машинство Пројектовање технолошких процеса Тема: Др Мијодраг Милошевић Технолошки процеси израде производа Део производног процеса у коме се врши измена
Matematicke metode fizike II - akademska 2012/2013.g.
 Besselove funkcije y(x) = m=0 a m x m+σ, x 2 y + xy + (x 2 ν 2 )y = 0 σ 2 = ν 2 (1 ± 2ν)a 1 = 0; n(n ± 2ν)a n + a n 2 = 0 za n 2. J ν (x) = n=0 Besselove funkcije prve vrste reda ν. ( 1) n ( x ) ν+2n n!γ(ν
Besselove funkcije y(x) = m=0 a m x m+σ, x 2 y + xy + (x 2 ν 2 )y = 0 σ 2 = ν 2 (1 ± 2ν)a 1 = 0; n(n ± 2ν)a n + a n 2 = 0 za n 2. J ν (x) = n=0 Besselove funkcije prve vrste reda ν. ( 1) n ( x ) ν+2n n!γ(ν
ЛИНЕАРНА ФУНКЦИЈА ЛИНЕАРНА ФУНКЦИЈА у = kх + n А утврди 1. Које од наведених функција су линеарне: а) у = 2х; б) у = 4х; в) у = 2х 7; г) у = 2 5 x; д)
 ЛИНЕАРНА ФУНКЦИЈА ЛИНЕАРНА ФУНКЦИЈА у = kх + n А утврди 1. Које од наведених функција су линеарне: а) у = х; б) у = 4х; в) у = х 7; г) у = 5 x; д) у = 5x ; ђ) у = х + х; е) у = x + 5; ж) у = 5 x ; з) у
ЛИНЕАРНА ФУНКЦИЈА ЛИНЕАРНА ФУНКЦИЈА у = kх + n А утврди 1. Које од наведених функција су линеарне: а) у = х; б) у = 4х; в) у = х 7; г) у = 5 x; д) у = 5x ; ђ) у = х + х; е) у = x + 5; ж) у = 5 x ; з) у
Microsoft Word - radnja_uvezivanje.doc
 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ELEKTROTEHNIČKI FAKULTET OSIJEK Tomislav Matić UTJECAJ KAŠNJENJA KOMPARATORA S HISTEREZOM NA SREDIŠNJU FREKVENCIJU ASINKRONOG SIGMA-DELTA MODULATORA Dotorsa
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ELEKTROTEHNIČKI FAKULTET OSIJEK Tomislav Matić UTJECAJ KAŠNJENJA KOMPARATORA S HISTEREZOM NA SREDIŠNJU FREKVENCIJU ASINKRONOG SIGMA-DELTA MODULATORA Dotorsa
1
 Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аут
 Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Иван Жупунски, Небојша Пјевалица, Марјан Урекар,
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Иван Жупунски, Небојша Пјевалица, Марјан Урекар,
Microsoft Word - rokovi_2019.docx
 4..019. pismeni ispit 1. Materijalna toča mase 0.5 miruje na hrapaoj osini (α=15 i μ=0.3), ad na nju počne djeloati osa sila (t) oja se mijenja prema priazanom dijaramu. Treba odrediti dijarame R(t), a(t)
4..019. pismeni ispit 1. Materijalna toča mase 0.5 miruje na hrapaoj osini (α=15 i μ=0.3), ad na nju počne djeloati osa sila (t) oja se mijenja prema priazanom dijaramu. Treba odrediti dijarame R(t), a(t)
Slide 1
 Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 1: Увод и историјски развој теорије система UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES Катедра за управљање системима Наставници:
Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 1: Увод и историјски развој теорије система UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES Катедра за управљање системима Наставници:
*ИЗВЈЕШТАЈ О ПРОВЕДЕНОЈ ПРЕВЕНТИВНОЈ АКТИВНОСТИ* "Возило након зимских услова 2015" АМС РС и ауто мото друштва у сарадњи са Министарством унутрашњих п
 *ИЗВЈЕШТАЈ О ПРОВЕДЕНОЈ ПРЕВЕНТИВНОЈ АКТИВНОСТИ* "Возило након зимских услова 2015" АМС РС и ауто мото друштва у сарадњи са Министарством унутрашњих послова Републике Српске и Министарством саобраћаја
*ИЗВЈЕШТАЈ О ПРОВЕДЕНОЈ ПРЕВЕНТИВНОЈ АКТИВНОСТИ* "Возило након зимских услова 2015" АМС РС и ауто мото друштва у сарадњи са Министарством унутрашњих послова Републике Српске и Министарством саобраћаја
Београд, МАТРИЧНА АНАЛИЗА КОНСТРУКЦИЈА ЗАДАТАК 1 За носач приказан на слици: а) одредити дужине извијања свих штапова носача, ако на носач
 Београд, 30.01.2016. а) одредити дужине извијања свих штапова носача, ако на носач делују само концентрисане силе, б) ако је P = 0.8P cr, и на носач делује расподељено оптерећење f, одредити моменат савијања
Београд, 30.01.2016. а) одредити дужине извијања свих штапова носача, ако на носач делују само концентрисане силе, б) ако је P = 0.8P cr, и на носач делује расподељено оптерећење f, одредити моменат савијања
Microsoft Word - IZVOD FUNKCIJE.doc
 IZVOD FUNKCIJE Predpotavimo da je funkcija f( definiana u nekom intervalu (a,b i da je tačka iz intervala (a,b fikirana. Uočimo neku proizvoljnu tačku iz tog intervala (a,b. Ova tačka može da e pomera
IZVOD FUNKCIJE Predpotavimo da je funkcija f( definiana u nekom intervalu (a,b i da je tačka iz intervala (a,b fikirana. Uočimo neku proizvoljnu tačku iz tog intervala (a,b. Ova tačka može da e pomera
Динамика крутог тела
 Динамика крутог тела. Задаци за вежбу 1. Штап масе m и дужине L се крајем А наслања на храпаву хоризонталну раван, док на другом крају дејствује сила F константног интензитета и правца нормалног на штап.
Динамика крутог тела. Задаци за вежбу 1. Штап масе m и дужине L се крајем А наслања на храпаву хоризонталну раван, док на другом крају дејствује сила F константног интензитета и правца нормалног на штап.
Microsoft Word - ROKI doc
 UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU Žarko M. Janković ODRŽAVANJE TEHNIČKIH SISTEMA Niš, 2017. ODRŽAVANJE TEHNIČKIH SISTEMA Autor Dr Žarko M. Janković, red. prof. Fakultet zaštite na radu
UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU Žarko M. Janković ODRŽAVANJE TEHNIČKIH SISTEMA Niš, 2017. ODRŽAVANJE TEHNIČKIH SISTEMA Autor Dr Žarko M. Janković, red. prof. Fakultet zaštite na radu
8. ( )
 8. Кинематика тачке (криволиниjско кретање) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj - Шта ћемо научити 1. Криволиниjско кретање Преглед
8. Кинематика тачке (криволиниjско кретање) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj - Шта ћемо научити 1. Криволиниjско кретање Преглед
СТЕПЕН појам и особине
 СТЕПЕН појам и особине Степен чији је изложилац природан број N R \ 0 изложилац (експонент) основа степен Особине: m m m m : m m : : Примери. 8 4 7 4 5 4 4 5 6 :5 Важно! 5 5 5 5 5 55 5 Основа је број -5
СТЕПЕН појам и особине Степен чији је изложилац природан број N R \ 0 изложилац (експонент) основа степен Особине: m m m m : m m : : Примери. 8 4 7 4 5 4 4 5 6 :5 Важно! 5 5 5 5 5 55 5 Основа је број -5
QFD METODA – PRIMER
 QFD METODA - PRIMER PROBLEM: U kompaniji X koja se bavi izradom kompjuterskih softvera uočen je pad prodaje konkretnog softvera - Softver za vođenje knjigovodstva. Kompanija X je raspolagala sa jednom
QFD METODA - PRIMER PROBLEM: U kompaniji X koja se bavi izradom kompjuterskih softvera uočen je pad prodaje konkretnog softvera - Softver za vođenje knjigovodstva. Kompanija X je raspolagala sa jednom
SIGURNOSNI NALOG BROJ: 2017/001 rev 01 SAFETY ORDER NUMBER: 2017/001 rev 01 Naslov: Sigurnosni nalog kojim se utvrđuju uslovi za upotrebu sistema besp
 SIGURNOSNI NALOG BROJ: 2017/001 rev 01 SAFETY ORDER NUMBER: 2017/001 rev 01 Naslov: Sigurnosni nalog kojim se utvrđuju uslovi za upotrebu sistema bespilotnih vazduhoplova i vazduhoplovnih modela u oblastima
SIGURNOSNI NALOG BROJ: 2017/001 rev 01 SAFETY ORDER NUMBER: 2017/001 rev 01 Naslov: Sigurnosni nalog kojim se utvrđuju uslovi za upotrebu sistema bespilotnih vazduhoplova i vazduhoplovnih modela u oblastima
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић
 Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Драган Пејић, Бојан Вујичић, Небојша Пјевалица,
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Драган Пејић, Бојан Вујичић, Небојша Пјевалица,
Microsoft Word - SIORT1_2019_K1_resenje.docx
 I колоквијум из Основа рачунарске технике I СИ- 208/209 (24.03.209.) Р е ш е њ е Задатак f(x, x 2, x 3 ) = (x + x x ) x (x x 2 + x ) + x x 2 x 3 f(x, x 2, x 3 ) = (x + x x ) (x x + (x )) 2 + x + x x 2
I колоквијум из Основа рачунарске технике I СИ- 208/209 (24.03.209.) Р е ш е њ е Задатак f(x, x 2, x 3 ) = (x + x x ) x (x x 2 + x ) + x x 2 x 3 f(x, x 2, x 3 ) = (x + x x ) (x x + (x )) 2 + x + x x 2
ИЗВЕШТАЈ О РЕЗУЛТАТИМА АНКЕТЕ О ИНФЛАЦИОНИМ OЧЕКИВАЊИМА Фебруар Београд, март 2019.
 ИЗВЕШТАЈ О РЕЗУЛТАТИМА АНКЕТЕ О ИНФЛАЦИОНИМ OЧЕКИВАЊИМА Фебруар 219. Београд, март 219. С А Д Р Ж А Ј Уводна напомена... 3 Резиме... 4 Инфлациона очекивања финансијског сектора... 5 Инфлациона очекивања
ИЗВЕШТАЈ О РЕЗУЛТАТИМА АНКЕТЕ О ИНФЛАЦИОНИМ OЧЕКИВАЊИМА Фебруар 219. Београд, март 219. С А Д Р Ж А Ј Уводна напомена... 3 Резиме... 4 Инфлациона очекивања финансијског сектора... 5 Инфлациона очекивања
PITANJA I ZADACI ZA II KOLOKVIJUM IZ MATEMATIKE I Pitanja o nizovima Nizovi Realni niz i njegov podniz. Tačka nagomilavanja niza i granična vrednost(l
 PITANJA I ZADACI ZA II KOLOKVIJUM IZ MATEMATIKE I Pitanja o nizovima Nizovi Realni niz i njegov podniz. Tačka nagomilavanja niza i granična vrednost(limes) niza. Svojstva konvergentnih nizova, posebno
PITANJA I ZADACI ZA II KOLOKVIJUM IZ MATEMATIKE I Pitanja o nizovima Nizovi Realni niz i njegov podniz. Tačka nagomilavanja niza i granična vrednost(limes) niza. Svojstva konvergentnih nizova, posebno
Републички педагошки завод Бања Лука Стручни савјетник за машинску групу предмета и практичну наставу Датум: године Тема: Елементи и начин
 Републички педагошки завод Бања Лука Стручни савјетник за машинску групу предмета и практичну наставу Датум:.06.2009. године Тема: Елементи и начин вредновања графичког рада из раванских носачи 1 Увод:
Републички педагошки завод Бања Лука Стручни савјетник за машинску групу предмета и практичну наставу Датум:.06.2009. године Тема: Елементи и начин вредновања графичког рада из раванских носачи 1 Увод:
PARCIJALNO MOLARNE VELIČINE
 PARCIJALNE MOLARNE VELIČINE ZATVOREN TERMODINAMIČKI SISTEM-konstantan sastav sistema Posmatra se neka termodinamička ekstenzivna veličina X X (V, U, H, G, A, S) X je u funkciji bilo kog para intenzivnih
PARCIJALNE MOLARNE VELIČINE ZATVOREN TERMODINAMIČKI SISTEM-konstantan sastav sistema Posmatra se neka termodinamička ekstenzivna veličina X X (V, U, H, G, A, S) X je u funkciji bilo kog para intenzivnih
My_ST_FTNIspiti_Free
 ИСПИТНИ ЗАДАЦИ СУ ГРУПИСАНИ ПО ТЕМАМА: ЛИМЕСИ ИЗВОДИ ФУНКЦИЈЕ ЈЕДНЕ ПРОМЕНЉИВЕ ИСПИТИВАЊЕ ТОКА ФУНКЦИЈЕ ЕКСТРЕМИ ФУНКЦИЈЕ СА ВИШЕ ПРОМЕНЉИВИХ 5 ИНТЕГРАЛИ ДОДАТАК ФТН Испити С т р а н а Лимеси Одредити
ИСПИТНИ ЗАДАЦИ СУ ГРУПИСАНИ ПО ТЕМАМА: ЛИМЕСИ ИЗВОДИ ФУНКЦИЈЕ ЈЕДНЕ ПРОМЕНЉИВЕ ИСПИТИВАЊЕ ТОКА ФУНКЦИЈЕ ЕКСТРЕМИ ФУНКЦИЈЕ СА ВИШЕ ПРОМЕНЉИВИХ 5 ИНТЕГРАЛИ ДОДАТАК ФТН Испити С т р а н а Лимеси Одредити
Ravno kretanje krutog tela
 Ravno kretanje krutog tela Brzine tačaka tela u reprezentativnom preseku Ubrzanja tačaka u reprezentativnom preseku Primer određivanja brzina i ubrzanja kod ravnog mehanizma Ravno kretanje krutog tela
Ravno kretanje krutog tela Brzine tačaka tela u reprezentativnom preseku Ubrzanja tačaka u reprezentativnom preseku Primer određivanja brzina i ubrzanja kod ravnog mehanizma Ravno kretanje krutog tela
9. : , ( )
 9. Динамика тачке: Енергиjа, рад и снага (први део) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj - Шта ћемо научити (1) 1. Преглед литературе
9. Динамика тачке: Енергиjа, рад и снага (први део) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj - Шта ћемо научити (1) 1. Преглед литературе
Microsoft PowerPoint - STABILNOST KONSTRUKCIJA 4_19 [Compatibility Mode]
![Microsoft PowerPoint - STABILNOST KONSTRUKCIJA 4_19 [Compatibility Mode] Microsoft PowerPoint - STABILNOST KONSTRUKCIJA 4_19 [Compatibility Mode]](/thumbs/99/141489570.jpg) Univerzitet u Beogradu Građevinski fakutet Katedra za tehničku mehaniku i teoriju konstrukcija STABILNOST KONSTRUKCIJA IV ČAS V. PROF. DR MARIJA NEFOVSKA DANILOVIĆ 3. SABILNOST KONSTRUKCIJA 1 Geometrijska
Univerzitet u Beogradu Građevinski fakutet Katedra za tehničku mehaniku i teoriju konstrukcija STABILNOST KONSTRUKCIJA IV ČAS V. PROF. DR MARIJA NEFOVSKA DANILOVIĆ 3. SABILNOST KONSTRUKCIJA 1 Geometrijska
PREDLOG ZAKON O IZMENAMA ZAKONA O FINANSIRANJU LOKALNE SAMOUPRAVE Član 1. U Zakonu o finansiranju lokalne samouprave ( Službeni glasnik RS, br. 62/06,
 PREDLOG ZAKON O IZMENAMA ZAKONA O FINANSIRANJU LOKALNE SAMOUPRAVE Član 1. U Zakonu o finansiranju lokalne samouprave ( Službeni glasnik RS, br. 6206, 4711, 9312, 9913, 12514 i 9515), u članu 35. stav 1.
PREDLOG ZAKON O IZMENAMA ZAKONA O FINANSIRANJU LOKALNE SAMOUPRAVE Član 1. U Zakonu o finansiranju lokalne samouprave ( Službeni glasnik RS, br. 6206, 4711, 9312, 9913, 12514 i 9515), u članu 35. stav 1.
ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 2006/2007 године I разред
 ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 006/007 године разред. Електрични систем се састоји из отпорника повезаних тако
ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 006/007 године разред. Електрични систем се састоји из отпорника повезаних тако
ПРИРОДА И ЗНАК РЕШЕЊА 2 b ax bx c 0 x1 x2 2 D b 4ac a ( сви задаци су решени) c b D xx 1 2 x1/2 a 2a УСЛОВИ Решења реална и различита D>0 Решења реалн
 ПРИРОДА И ЗНАК РЕШЕЊА ax x c 0 x x D 4ac a ( сви задаци су решени) c D xx x/ a a УСЛОВИ Решења реална и различита D>0 Решења реална D Двоструко решење (реална и једнака решења) D=0 Комплексна решења (нису
ПРИРОДА И ЗНАК РЕШЕЊА ax x c 0 x x D 4ac a ( сви задаци су решени) c D xx x/ a a УСЛОВИ Решења реална и различита D>0 Решења реална D Двоструко решење (реална и једнака решења) D=0 Комплексна решења (нису
Задатак 4: Центрифугална пумпа познате карактеристике при n = 2900 min -1 ради на инсталацији приказаној на слици и потискује воду из резервоара А у р
 Задатак 4: Центрифугална пумпа познате карактеристике при n = 900 min -1 ради на инсталацији приказаној на слици и потискује воду из резервоара А у резервоар B. Непосредно на излазу из пумпе постављен
Задатак 4: Центрифугална пумпа познате карактеристике при n = 900 min -1 ради на инсталацији приказаној на слици и потискује воду из резервоара А у резервоар B. Непосредно на излазу из пумпе постављен
STABILNOST SISTEMA
 STABILNOST SISTEMA Najvaznija osobina sistema automatskog upravljanja je stabilnost. Generalni zahtev koji se postavlja pred projektanta jeste da projektovani i realizovani sistem automatskog upravljanja
STABILNOST SISTEMA Najvaznija osobina sistema automatskog upravljanja je stabilnost. Generalni zahtev koji se postavlja pred projektanta jeste da projektovani i realizovani sistem automatskog upravljanja
Univerzitet u Beogradu Elektrotehnički fakultet Katedra za energetske pretvarače i pogone ISPIT IZ SINHRONIH MAŠINA (13E013SIM) 1. Poznati su podaci o
 Univerzitet u Beogradu Elektrotehnički akultet Katedra za energetske pretvarače i pogone ISPIT IZ SINHRONIH MAŠINA (13E013SIM) 1. Poznati su podaci o namotaju statora sinhronog motora sa stalnim magnetima
Univerzitet u Beogradu Elektrotehnički akultet Katedra za energetske pretvarače i pogone ISPIT IZ SINHRONIH MAŠINA (13E013SIM) 1. Poznati su podaci o namotaju statora sinhronog motora sa stalnim magnetima
Microsoft Word - Algebra i funkcije- napredni nivo doc
 Algebra i funkcije napredni nivo 01. Nenegativna znači da je vrednost izraza pozitivna ili je jednaka 0. ( 1) ( 1)( 1) 0 razlika kvadrata (( x) + x 1+ 1 ) (( x) 1 ) 0 ( + + 1) ( 1) 0 x x+ x x+ x x x +
Algebra i funkcije napredni nivo 01. Nenegativna znači da je vrednost izraza pozitivna ili je jednaka 0. ( 1) ( 1)( 1) 0 razlika kvadrata (( x) + x 1+ 1 ) (( x) 1 ) 0 ( + + 1) ( 1) 0 x x+ x x+ x x x +
PowerPoint Presentation
 Универзитет у Нишу Електронски факултет у Нишу Катедра за теоријску електротехнику ЛАБОРАТОРИЈСКИ ПРАКТИКУМ ОСНОВИ ЕЛЕКТРОТЕХНИКЕ Примена програмског пакета FEMM у електротехници ВЕЖБЕ 3 И 4. Електростатика
Универзитет у Нишу Електронски факултет у Нишу Катедра за теоријску електротехнику ЛАБОРАТОРИЈСКИ ПРАКТИКУМ ОСНОВИ ЕЛЕКТРОТЕХНИКЕ Примена програмског пакета FEMM у електротехници ВЕЖБЕ 3 И 4. Електростатика
Analiticka geometrija
 Analitička geometrija Predavanje 3 Konusni preseci (krive drugog reda, kvadratne krive) Novi Sad, 2018. Milica Žigić (PMF, UNS 2018) Analitička geometrija predavanje 3 1 / 22 Ime s obzirom na karakteristike
Analitička geometrija Predavanje 3 Konusni preseci (krive drugog reda, kvadratne krive) Novi Sad, 2018. Milica Žigić (PMF, UNS 2018) Analitička geometrija predavanje 3 1 / 22 Ime s obzirom na karakteristike
Испитни задаци - Задатак 1 Задатак 1 (23. септембар 2012.) а) Статичком методом конструисати утицајне линије за силе у штаповима V b и D 4. б) Одредит
 Испитни задаци - Задатак 1 Задатак 1 (23. септембар 2012.) а) Статичком методом конструисати утицајне линије за силе у штаповима V b и D 4. б) Одредити max D 4 услед задатог покретног система концентрисаних
Испитни задаци - Задатак 1 Задатак 1 (23. септембар 2012.) а) Статичком методом конструисати утицајне линије за силе у штаповима V b и D 4. б) Одредити max D 4 услед задатог покретног система концентрисаних
kvadratna jednačina - zadaci za vežbanje (Vladimir Marinkov).nb 1 Kvadratna jednačina 1. Rešiti jednačine: a x 2 81 b 2 x 2 50 c 4 x d x 1
 kvadratna jednačina - zadaci za vežbanje 0. (Vladimir Marinkov).nb Kvadratna jednačina. Rešiti jednačine: a x 8 b x 0 c x d x x x e x x x f x 8 x 6 x x 6 rešenje: a) x,, b x,, c x,,d x, 6, e x,, (f) x,.
kvadratna jednačina - zadaci za vežbanje 0. (Vladimir Marinkov).nb Kvadratna jednačina. Rešiti jednačine: a x 8 b x 0 c x d x x x e x x x f x 8 x 6 x x 6 rešenje: a) x,, b x,, c x,,d x, 6, e x,, (f) x,.
Republika e Kosovës Republika Kosovo Republic of Kosovo Autoriteti i Aviacionit Civil i Kosovës Autoritet Civilnog Vazduhoplovstva Kosova Civil Aviati
 Republika e Kosovës Republika Kosovo Republic of Kosovo Autoriteti i Aviacionit Civil i Kosovës Autoritet Civilnog Vazduhoplovstva Kosova Civil Aviation Authority of Kosovo Generalni direktor Autoriteta
Republika e Kosovës Republika Kosovo Republic of Kosovo Autoriteti i Aviacionit Civil i Kosovës Autoritet Civilnog Vazduhoplovstva Kosova Civil Aviation Authority of Kosovo Generalni direktor Autoriteta
Microsoft Word - 7. cas za studente.doc
 VII Диферeнцни поступак Користи се за решавање диференцијалних једначина. Интервал на коме је дефинисана тражена функција се издели на делова. Усвоји се да се непозната функција између сваке три тачке
VII Диферeнцни поступак Користи се за решавање диференцијалних једначина. Интервал на коме је дефинисана тражена функција се издели на делова. Усвоји се да се непозната функција између сваке три тачке
I колоквијум из Основа рачунарске технике I СИ- 2017/2018 ( ) Р е ш е њ е Задатак 1 Тачка А Потребно је прво пронаћи вредности функција f(x
 I колоквијум из Основа рачунарске технике I СИ- / (...) Р е ш е њ е Задатак Тачка А Потребно је прво пронаћи вредности функција f(x, x, x ) и g(x, x, x ) на свим векторима. f(x, x, x ) = x x + x x + x
I колоквијум из Основа рачунарске технике I СИ- / (...) Р е ш е њ е Задатак Тачка А Потребно је прво пронаћи вредности функција f(x, x, x ) и g(x, x, x ) на свим векторима. f(x, x, x ) = x x + x x + x
UNAPREĐENJE ENERGETSKE EFIKASNOSTI GRADSKOG SISTEMA ZA UPRAVLJANJE ČVRSTIM OTPADOM
 Univerzitet u Kragujevcu Mašinski fakultet Kragujevac University of Kragujevac Faculty of Mechanical Engineering Kragujevac IMPROVING MUNICIPAL SYSTEM FOR SOLID WASTE MANAGEMENT USING GIS-TEHNIQUES AND
Univerzitet u Kragujevcu Mašinski fakultet Kragujevac University of Kragujevac Faculty of Mechanical Engineering Kragujevac IMPROVING MUNICIPAL SYSTEM FOR SOLID WASTE MANAGEMENT USING GIS-TEHNIQUES AND
PowerPoint Presentation
 Matrica šansi-pretnji Matrica šansi-pretnji Matrica šansi-pretnji se bavi dijagnozom situacije u kojoj se preduzeće nalazi, kao i njenom projekcijom u budućnosti (dijagnoza + prognoza). Situaciona analiza,
Matrica šansi-pretnji Matrica šansi-pretnji Matrica šansi-pretnji se bavi dijagnozom situacije u kojoj se preduzeće nalazi, kao i njenom projekcijom u budućnosti (dijagnoza + prognoza). Situaciona analiza,
На основу члана 15. и члана 59. став 2. Закона о Агенцији за борбу против корупције ( Службени гласник РС, бр. 97/08, 53/10, 66/11 - одлука УС, 67/13
 На основу члана 15. и члана 59. став 2. Закона о Агенцији за борбу против корупције ( Службени гласник РС, бр. 97/08, 53/10, 66/11 - одлука УС, 67/13 - одлука УС, 112/13 - аутентично тумачење и 8/15 -
На основу члана 15. и члана 59. став 2. Закона о Агенцији за борбу против корупције ( Службени гласник РС, бр. 97/08, 53/10, 66/11 - одлука УС, 67/13 - одлука УС, 112/13 - аутентично тумачење и 8/15 -
ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ
 Универзитет у Београду, Електротехнички факултет, Катедра за енергетске претвараче и погоне ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ (3Е3ЕНТ) Јул 9. Трофазни уљни енергетски трансформатор са номиналним подацима: 4 V,
Универзитет у Београду, Електротехнички факултет, Катедра за енергетске претвараче и погоне ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ (3Е3ЕНТ) Јул 9. Трофазни уљни енергетски трансформатор са номиналним подацима: 4 V,
Microsoft PowerPoint - STABILNOST KONSTRUKCIJA 2_18 [Compatibility Mode]
![Microsoft PowerPoint - STABILNOST KONSTRUKCIJA 2_18 [Compatibility Mode] Microsoft PowerPoint - STABILNOST KONSTRUKCIJA 2_18 [Compatibility Mode]](/thumbs/99/140947091.jpg) 6. STABILNOST KONSTRUKCIJA II čas Marija Nefovska-Danilović 3. Stabilnost konstrukcija 1 6.2 Osnovne jednačine štapa 6.2.1 Linearna teorija štapa Važe pretpostavke o geometrijskoj (1), statičkoj (2) i
6. STABILNOST KONSTRUKCIJA II čas Marija Nefovska-Danilović 3. Stabilnost konstrukcija 1 6.2 Osnovne jednačine štapa 6.2.1 Linearna teorija štapa Važe pretpostavke o geometrijskoj (1), statičkoj (2) i
РЕШЕЊА 1. (2) Обележја статистичких јединица посматрања су: а) особине које су заједничке за јединице посматрања б) особине које се проучавају, а подр
 РЕШЕЊА. () Обележја статистичких јединица посматрања су: а) особине које су заједничке за јединице посматрања б) особине које се проучавају, а подразумевају различите вредности по јединицама посматрања
РЕШЕЊА. () Обележја статистичких јединица посматрања су: а) особине које су заједничке за јединице посматрања б) особине које се проучавају, а подразумевају различите вредности по јединицама посматрања
Секретаријат за заштиту животне средине града Београда – Прилагођавање климатским променама, Програма заштите животне средине и могућу утицај на урбан
 Град Београд Прилагођавање климатским променама - Програм заштите животне средине и могућу утицај на урбани развој Београда Др Сњежана Глумац Секретаријат за заштиту животне средине Београд 09.11.2015.
Град Београд Прилагођавање климатским променама - Програм заштите животне средине и могућу утицај на урбани развој Београда Др Сњежана Глумац Секретаријат за заштиту животне средине Београд 09.11.2015.
ОПШТИНЕ ВЕЛИКО ГРАДИШТЕ Година XV Број 12 ВЕЛИКО ГРАДИШТЕ 18. септембар На основу члана 64. став 3. Закона о пољопривредном земљишту («Сл.гласни
 ОПШТИНЕ ВЕЛИКО ГРАДИШТЕ Година XV Број 12 ВЕЛИКО ГРАДИШТЕ 18. септембар 2018. На основу члана 64. став 3. Заона о пољопривредном земљишту («Сл.гласни РС», број 62/06, 69/08-др заон, 41/09, 112/15 и 80/17),
ОПШТИНЕ ВЕЛИКО ГРАДИШТЕ Година XV Број 12 ВЕЛИКО ГРАДИШТЕ 18. септембар 2018. На основу члана 64. став 3. Заона о пољопривредном земљишту («Сл.гласни РС», број 62/06, 69/08-др заон, 41/09, 112/15 и 80/17),
PowerPoint Presentation
 Показатељи технолошког напретка Технолошки развој Резултира стварањем нових или побољшањем постојећих производа, процеса и услуга. Технолошки развој - део економског и друштвеног развоја. Научни и технолошки
Показатељи технолошког напретка Технолошки развој Резултира стварањем нових или побољшањем постојећих производа, процеса и услуга. Технолошки развој - део економског и друштвеног развоја. Научни и технолошки
Predavanje 8-TEMELJI I POTPORNI ZIDOVI.ppt
 1 BETONSKE KONSTRUKCIJE TEMELJI OBJEKATA Prof. dr Snežana Marinković Doc. dr Ivan Ignjatović Semestar: V ESPB: Temelji objekata 2 1.1. Podela 1.2. Temelji samci 1.3. Temeljne trake 1.4. Temeljne grede
1 BETONSKE KONSTRUKCIJE TEMELJI OBJEKATA Prof. dr Snežana Marinković Doc. dr Ivan Ignjatović Semestar: V ESPB: Temelji objekata 2 1.1. Podela 1.2. Temelji samci 1.3. Temeljne trake 1.4. Temeljne grede
Microsoft Word - Ispitivanje toka i grafik funkcije V deo
 . Ispitati tok i skicirati grafik funkcije y= arcsin + Oblast definisanosti (domen) Podsetimo se grafika elementarnih funkcija i kako izgleda arcsin funkcija: y - y=arcsin Funkcija je definisana za [,]
. Ispitati tok i skicirati grafik funkcije y= arcsin + Oblast definisanosti (domen) Podsetimo se grafika elementarnih funkcija i kako izgleda arcsin funkcija: y - y=arcsin Funkcija je definisana za [,]
АНАЛИЗА ПРОБЛЕМА ТЕРМИЧКЕ ДИЛАТАЦИЈЕ L КОМПЕНЗАТОРА ПРЕМА СТАНДАРДУ AD 2000 И ДРУГИМ МЕТОДАМА Милан Травица Иновациони центар Машински факултет Универ
 АНАЛИЗА ПРОБЛЕМА ТЕРМИЧКЕ ДИЛАТАЦИЈЕ L КОМПЕНЗАТОРА ПРЕМА СТАНДАРДУ AD 2000 И ДРУГИМ МЕТОДАМА Милан Травица Иновациони центар Машински факултет Универзитет у Београду Краљице Марије 16, 11000 Београд mtravica@mas.bg.ac.rs
АНАЛИЗА ПРОБЛЕМА ТЕРМИЧКЕ ДИЛАТАЦИЈЕ L КОМПЕНЗАТОРА ПРЕМА СТАНДАРДУ AD 2000 И ДРУГИМ МЕТОДАМА Милан Травица Иновациони центар Машински факултет Универзитет у Београду Краљице Марије 16, 11000 Београд mtravica@mas.bg.ac.rs
Na osnovu člana 43 stav 4 tačka 2 Zakona o energetici (''Službeni list CG'', broj 5/16 i 51/17) i člana 12 stav 1 tačka 1 Statuta Regulatorne agencije
 Na osnovu člana 43 stav 4 tačka 2 Zakona o energetici (''Službeni list CG'', broj 5/16 i 51/17) i člana 12 stav 1 tačka 1 Statuta Regulatorne agencije za energetiku (''Službeni list CG'', broj 36/17),
Na osnovu člana 43 stav 4 tačka 2 Zakona o energetici (''Službeni list CG'', broj 5/16 i 51/17) i člana 12 stav 1 tačka 1 Statuta Regulatorne agencije za energetiku (''Službeni list CG'', broj 36/17),
ASHRAE Region-At-Large Conference March , 2010
 2. Međunarodni stručni skup iz oblasti klimatizacije, grejanja i hlađenja, 22-23. sep. 2016. Budva, Crna Gora Sprega solarnog sistema sa toplotnim pumpama snage grejanja oko 1 MW - više od 30 godina u
2. Međunarodni stručni skup iz oblasti klimatizacije, grejanja i hlađenja, 22-23. sep. 2016. Budva, Crna Gora Sprega solarnog sistema sa toplotnim pumpama snage grejanja oko 1 MW - više od 30 godina u
Microsoft PowerPoint - Teorija kretanja vozila-predavanje 3.1.ppt
 ТЕОРИЈА КРЕТАЊА ВОЗИЛА Предавање. гусенична возила, површински притисак ослањања, гусеница на подлогу ослањања G=mg p p гусеница на подлогу ослањања G=mg средњи стварни p тврда подлога средњи стварни p
ТЕОРИЈА КРЕТАЊА ВОЗИЛА Предавање. гусенична возила, површински притисак ослањања, гусеница на подлогу ослањања G=mg p p гусеница на подлогу ослањања G=mg средњи стварни p тврда подлога средњи стварни p
PowerPoint Presentation
 Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Microsoft PowerPoint - DS-1-16 [Compatibility Mode]
![Microsoft PowerPoint - DS-1-16 [Compatibility Mode] Microsoft PowerPoint - DS-1-16 [Compatibility Mode]](/thumbs/102/155207709.jpg) Ekonometrija 1-D Analiza vremenskih serija Predavač: Zorica Mladenović, zorima@eunet.rs, http://avs.ekof.bg.ac.rs kabinet: 414 1 Struktura predmeta Izučavaju se dve oblasti: Analiza vremenskih serija Analiza
Ekonometrija 1-D Analiza vremenskih serija Predavač: Zorica Mladenović, zorima@eunet.rs, http://avs.ekof.bg.ac.rs kabinet: 414 1 Struktura predmeta Izučavaju se dve oblasti: Analiza vremenskih serija Analiza
Зборник радова 6. Међународне конференције о настави физике у средњим школама, Алексинац, март Одређивање коефицијента пригушења у ваздуху
 Одређивање коефицијента пригушења у ваздуху помоћу линеарног хармонијског осцилатора Соња Ковачевић 1, Милан С. Ковачевић 2 1 Прва крагујевачка гимназија, Крагујевац, Србија 2 Природно-математички факултет,
Одређивање коефицијента пригушења у ваздуху помоћу линеарног хармонијског осцилатора Соња Ковачевић 1, Милан С. Ковачевић 2 1 Прва крагујевачка гимназија, Крагујевац, Србија 2 Природно-математички факултет,
07jeli.DVI
 Osječki matematički list 1(1), 85 94 85 Primjena karakterističnih funkcija u statistici Slobodan Jelić Sažetak. U ovom radu odred ene su funkcije distribucije aritmetičke sredine slučajnog uzorka duljine
Osječki matematički list 1(1), 85 94 85 Primjena karakterističnih funkcija u statistici Slobodan Jelić Sažetak. U ovom radu odred ene su funkcije distribucije aritmetičke sredine slučajnog uzorka duljine
Slide 1
 Анализа електроенергетских система -Прорачун кратких спојева- Кратак спој представља поремећено стање мреже, односно поремећено стање система. За време трајања кратког споја напони и струје се мењају са
Анализа електроенергетских система -Прорачун кратких спојева- Кратак спој представља поремећено стање мреже, односно поремећено стање система. За време трајања кратког споја напони и струје се мењају са
oae_10_dom
 ETF U BEOGRADU, ODSEK ZA ELEKTRONIKU Milan Prokin Radivoje Đurić domaći zadaci - 2010 1. Domaći zadatak 1.1. a) [4] Nacrtati direktno spregnut pojačavač (bez upotrebe sprežnih kondenzatora) sa NPN tranzistorima
ETF U BEOGRADU, ODSEK ZA ELEKTRONIKU Milan Prokin Radivoje Đurić domaći zadaci - 2010 1. Domaći zadatak 1.1. a) [4] Nacrtati direktno spregnut pojačavač (bez upotrebe sprežnih kondenzatora) sa NPN tranzistorima
Microsoft PowerPoint - Teorija kretanja vozila-predavanje 4.1.ppt
 ТЕОРИЈА КРЕТАЊА ВОЗИЛА Предавање 4.1 гусенична возила, отпори кретања, Код дефинисања параметара функција кретања возила на гусеницама разматрају се следећи случајеви кретања: а) праволиниjско кретање
ТЕОРИЈА КРЕТАЊА ВОЗИЛА Предавање 4.1 гусенична возила, отпори кретања, Код дефинисања параметара функција кретања возила на гусеницама разматрају се следећи случајеви кретања: а) праволиниjско кретање
48. РЕПУБЛИЧКО ТАКМИЧЕЊЕ ИЗ ФИЗИКЕ УЧЕНИКА СРЕДЊИХ ШКОЛА ШКОЛСКЕ 2009/2010. ГОДИНЕ I РАЗРЕД Друштво Физичара Србије Министарство Просвете Републике Ср
 I РАЗРЕД Друштво Физичара Србије Министарство Просвете Републике Србије ЗАДАЦИ ГИМНАЗИЈА ВЕЉКО ПЕТРОВИЋ СОМБОР 7.0.00.. На слици је приказана шема електричног кола. Електромоторна сила извора је ε = 50
I РАЗРЕД Друштво Физичара Србије Министарство Просвете Републике Србије ЗАДАЦИ ГИМНАЗИЈА ВЕЉКО ПЕТРОВИЋ СОМБОР 7.0.00.. На слици је приказана шема електричног кола. Електромоторна сила извора је ε = 50
TEORIJA SIGNALA I INFORMACIJA
 Multiple Input/Multiple Output sistemi MIMO sistemi Ulazi (pobude) Izlazi (odzivi) u 1 u 2 y 1 y 2 u k y r Obrada=Matematički model Načini realizacije: fizički sistemi (hardware) i algoritmi (software)
Multiple Input/Multiple Output sistemi MIMO sistemi Ulazi (pobude) Izlazi (odzivi) u 1 u 2 y 1 y 2 u k y r Obrada=Matematički model Načini realizacije: fizički sistemi (hardware) i algoritmi (software)
Mere slicnosti
 Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
?? ????????? ?????????? ?????? ?? ????????? ??????? ???????? ?? ??????? ??????:
 РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 003 АСИНХРОНЕ МАШИНЕ Трофазни асинхрони мотор са намотаним ротором има податке: 380V 10A cos ϕ 08 Y 50Hz p отпор статора R s Ω Мотор је испитан
РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 003 АСИНХРОНЕ МАШИНЕ Трофазни асинхрони мотор са намотаним ротором има податке: 380V 10A cos ϕ 08 Y 50Hz p отпор статора R s Ω Мотор је испитан
My_P_Trigo_Zbir_Free
 Штa треба знати пре почетка решавања задатака? ТРИГОНОМЕТРИЈА Ниво - Основне формуле које произилазе из дефиниција тригонометријских функција Тригонометријске функције се дефинишу у правоуглом троуглу
Штa треба знати пре почетка решавања задатака? ТРИГОНОМЕТРИЈА Ниво - Основне формуле које произилазе из дефиниција тригонометријских функција Тригонометријске функције се дефинишу у правоуглом троуглу
ma??? - Primer 1 Spregnuta ploca
 Primer 1 - proračun spregnute ploče na profilisanom limu 1. Karakteristike spregnute ploče Spregnuta ploča je raspona 4 m. Predviđen je jedan privremeni oslonac u polovini raspona ploče u toku građenja.
Primer 1 - proračun spregnute ploče na profilisanom limu 1. Karakteristike spregnute ploče Spregnuta ploča je raspona 4 m. Predviđen je jedan privremeni oslonac u polovini raspona ploče u toku građenja.
Рационални Бројеви Скуп рационалних бројева 1. Из скупа { 3 4, 2, 4, 11, 0, , 1 5, 12 3 } издвој подскуп: а) природних бројева; б) целих броје
 Рационални Бројеви Скуп рационалних бројева. Из скупа {,,,, 0,,, } издвој подскуп: а) природних бројева; б) целих бројева; в) ненегативних рационалних бројева; г) негативних рационалних бројева.. Запиши
Рационални Бројеви Скуп рационалних бројева. Из скупа {,,,, 0,,, } издвој подскуп: а) природних бројева; б) целих бројева; в) ненегативних рационалних бројева; г) негативних рационалних бројева.. Запиши
CRNOGORSKI KOMITET CIGRE Fuštić Željko doc. dr Martin Ćalasan Elektrotehnički fakultet,ucg Simulacione i eksperim
 CRNOGORSKI KOMITET CIGRE Fuštić Željko zeljkofustic@gmail.com doc. dr Martin Ćalasan Elektrotehnički fakultet,ucg martinc@ac.me Simulacione i eksperimentalne karakteristike asinhronog generatora KRATAK
CRNOGORSKI KOMITET CIGRE Fuštić Željko zeljkofustic@gmail.com doc. dr Martin Ćalasan Elektrotehnički fakultet,ucg martinc@ac.me Simulacione i eksperimentalne karakteristike asinhronog generatora KRATAK
PRIRODNO MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA RAČUNARSKE NAUKE Utorak, godine PRIJEMNI ISPIT IZ INFORMATIKE 1. Koja od navedenih ekste
 PRIRODNO MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA RAČUNARSKE NAUKE Utorak, 5.06.019. godine PRIJEMNI ISPIT IZ INFORMATIKE 1. Koja od navedenih ekstenzija se najčešće koristi za tekstualne datoteke? a)
PRIRODNO MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA RAČUNARSKE NAUKE Utorak, 5.06.019. godine PRIJEMNI ISPIT IZ INFORMATIKE 1. Koja od navedenih ekstenzija se najčešće koristi za tekstualne datoteke? a)
Microsoft Word - NULE FUNKCIJE I ZNAK FUNKCIJE.doc
 NULE FUNKCIJE I ZNAK FUNKCIJE NULE FUNKCIJE su mesta gde grafik seče osu a dobijaju se kao rešenja jednačine y= 0 ( to jest f ( ) = 0 ) Mnogi profesori vole da se u okviru ove tačke nadje i presek sa y
NULE FUNKCIJE I ZNAK FUNKCIJE NULE FUNKCIJE su mesta gde grafik seče osu a dobijaju se kao rešenja jednačine y= 0 ( to jest f ( ) = 0 ) Mnogi profesori vole da se u okviru ove tačke nadje i presek sa y
Tабела А1 СТАЖ (СТАРОСТ) УКУПНО ЗАПОСЛЕНИХ ПРЕГЛЕД БРОЈА И СТРУКТУРЕ ЗАПОСЛЕНИХ СРБИЈА ВОЗ АД (на дан године) К В А Л И Ф И К А Ц И О Н А
 Tабела А1 СТАЖ (СТАРОСТ) УКУПНО ЗАПОСЛЕНИХ ПРЕГЛЕД БРОЈА И СТРУКТУРЕ ЗАПОСЛЕНИХ СРБИЈА ВОЗ АД (на дан 31.12.2015. године) К В А Л И Ф И К А Ц И О Н А С Т Р У К Т У Р А Прилог 1. НИЖА КВ СРЕДЊА ВКВ ВИША
Tабела А1 СТАЖ (СТАРОСТ) УКУПНО ЗАПОСЛЕНИХ ПРЕГЛЕД БРОЈА И СТРУКТУРЕ ЗАПОСЛЕНИХ СРБИЈА ВОЗ АД (на дан 31.12.2015. године) К В А Л И Ф И К А Ц И О Н А С Т Р У К Т У Р А Прилог 1. НИЖА КВ СРЕДЊА ВКВ ВИША
Slide 1
 Betonske konstrukcije 1 - vežbe 4 - Dijagram interakcije Građevinski fakultet Univerziteta u Beogradu Betonske konstrukcije 1 1 Građevinski fakultet Univerziteta u Beogradu Betonske konstrukcije 1 1 2
Betonske konstrukcije 1 - vežbe 4 - Dijagram interakcije Građevinski fakultet Univerziteta u Beogradu Betonske konstrukcije 1 1 Građevinski fakultet Univerziteta u Beogradu Betonske konstrukcije 1 1 2
Poštovani, U saopštenju Istraživanje i razvoj, godina broj 24, od 1. februara godine, uočena je greška, nastala iz pogrešno popunjenog upi
 Poštovani, U saopštenju Istraživanje i razvoj, 2011. godina broj 24, od 1. februara 2013. godine, uočena je greška, nastala iz pogrešno popunjenog upitnika izvještajne jedinice - Kliničko bolnički centar
Poštovani, U saopštenju Istraživanje i razvoj, 2011. godina broj 24, od 1. februara 2013. godine, uočena je greška, nastala iz pogrešno popunjenog upitnika izvještajne jedinice - Kliničko bolnički centar
06.ЈУЛ 2016 СЛУЖБЕНИ ЛИСТ општине Књажевац ГОДИНА X БРОЈ МАРТ 2017 БЕСПЛАТАН ПРИМЕРАК 1 На основу члана 81. Закона о буџетском систему ("Сл. гла
 06.ЈУЛ 2016 СЛУЖБЕНИ ЛИСТ општине Књажевац ГОДИНА X БРОЈ 03 17.МАРТ 2017 БЕСПЛАТАН ПРИМЕРАК 1 На основу члана 81. Закона о буџетском систему ("Сл. гласник РС", бр. 54/2009, 73/2010, 101/2010, 101/2011,
06.ЈУЛ 2016 СЛУЖБЕНИ ЛИСТ општине Књажевац ГОДИНА X БРОЈ 03 17.МАРТ 2017 БЕСПЛАТАН ПРИМЕРАК 1 На основу члана 81. Закона о буџетском систему ("Сл. гласник РС", бр. 54/2009, 73/2010, 101/2010, 101/2011,
Правилник o допунама Правилника о ограничењима и забранама производње, стављања у промет и коришћења хемикалија Члан 1. У Правилнику о ограничењима и
 Правилник o допунама Правилника о ограничењима и забранама производње, стављања у промет и коришћења хемикалија Члан 1. У Правилнику о ограничењима и забранама производње, стављања у промет и коришћења
Правилник o допунама Правилника о ограничењима и забранама производње, стављања у промет и коришћења хемикалија Члан 1. У Правилнику о ограничењима и забранама производње, стављања у промет и коришћења
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica
 Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
Projektovanje informacionih sistema i baze podataka
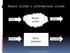 Realni sistem i informacioni sistem Ulaz Realni sistem Izlaz Unos Baza podataka Izveštaji Realni sistem i informacioni sistem Sistem se definiše kao skup objekata (entiteta) i njihovih međusobnih veza
Realni sistem i informacioni sistem Ulaz Realni sistem Izlaz Unos Baza podataka Izveštaji Realni sistem i informacioni sistem Sistem se definiše kao skup objekata (entiteta) i njihovih međusobnih veza
Microsoft PowerPoint - IS_G_predavanja_ [Compatibility Mode]
![Microsoft PowerPoint - IS_G_predavanja_ [Compatibility Mode] Microsoft PowerPoint - IS_G_predavanja_ [Compatibility Mode]](/thumbs/103/157511151.jpg) INŽENJERSKE SIMULACIJE Aleksandar Karač Kancelarija 1111 tel: 44 91 20, lok. 129 akarac@ptf.unze.ba Nermin Redžić Kancelarija 4202 tel: 44 91 20, lok.128 nermin.redzic@ptf.unze.ba www.ptf.unze.ba http://ptf.unze.ba/inzenjerske-simulacije
INŽENJERSKE SIMULACIJE Aleksandar Karač Kancelarija 1111 tel: 44 91 20, lok. 129 akarac@ptf.unze.ba Nermin Redžić Kancelarija 4202 tel: 44 91 20, lok.128 nermin.redzic@ptf.unze.ba www.ptf.unze.ba http://ptf.unze.ba/inzenjerske-simulacije
