Microsoft Word - Document1
|
|
|
- Ivanka Veselinović
- пре 6 година
- Прикази:
Транскрипт
1 10. Veza izeđu dva eleenta porojenja 110kV sa potporni izolatoria na nosačia izvedena je užadia Al/Fe 40/40 (slika ). Odrediti sile koje djeluju na ove potporne izolatore. Potrebni podaci za proračun su sljedeći: Oznaka Naziv Vrijedno σ nd,-0ºc atičko naprezanje užeta pri teperaturi -0 ºC 1.48 N/ σ nd,60ºc atičko naprezanje užeta pri teperaturi 60 ºC N/ " Efektivna vrijedno naizjenične koponente I k ruje KS u subtranzijentno periodu 19 ka a Razak izeđu centara provodnika l Raojanje izeđu nosača 8 k Vrijee trajanja kratkog spoja 0.5 s Masa provodnika po jedinici dužine kg/ E Jungov oduo elaičnoi N/ Slika. Veza izeđu dva eleenta u porojenju ovarena Al/Fe užeto Rješenje: Za vrijee trajanja i nakon završetka kratkog spoja na provodnike od Al/Fe užadi (bez provodnika u snopu) djeluju dvije vre sila: - sila zatezanja provodnika u sjeru otklona provodnika F t - sila usljed pada provodnika nakon kratkog spoja F f Kao jerodavna sila za nosače sa potporni izolatoria bira se veća sila od vrijednoi 1.5 F t i F f tj. Poupak proračuna ide sljedeći toko: F=ax{1.5 F t, F f } Sila po jedinici dužine užaog provodnika računa se po relaciji: " 0 Ik µ F' = 0.75 π a " I - efektivna vrijedno naizjenične koponente ukupne ruje KS u subtranzijentno periodu; l c l
2 a - razak izeđu centara provodnika; = za nosače sa potporni izolatoria ( ) " 7 0 I k l c 4 10 µ π F' = 0.75 = 0.75 = N/ π a l π Važan paraetar za dalji proračun sila na nosače je odnos elektroagnetne sile u uslovia kratkog spoja i gravitacione sile na provodnik dat kao: g ubrzanje Zeljine teže asa provodnika po jedinici dužine F' r= ' g F' r =.80 ' g = = Pravac rezultujuće sile na provodnik određen je uglo: δ 1= arctg() r = arctg(.80) = 70.4 Ekvivalentni atički ugib provodnika u sredini raspona je: ' g l bc = 8 F F atička sila zatezanja provodnika Odavde proračun treba sprovei za dvije sile zatezanja, i to pri teperaturi -0ºC i pri teperaturi 60 ºC. Pošto su data atička naprezanja provodnika pri ovi teperaturaa ia se: F =σ A = 1.48 (40+ 40) = 400 N, 0ºC, 0ºC s F =σ A = (40+ 40) = 73 N,60ºC,60ºC s A s ukupni presjek užeta Al/Fe 40/40 Sada se dobija: rana
3 ' g l bc, 0 = = = F ' g l bc,60 = = = F 8 73 Period oscilacija provodnika je: b = π 0.8 c g Zajeno brojnih podataka se dobija: bc, = π 0.8 = π 0.8 = s g 9.81 bc, = π 0.8 = π 0.8 = s g 9.81 Rezultujući period oscilacije provodnika res toko proticanja ruje kratkog spoja je dat kao: res= [s] 4 π δ 1 1+ r res, 0 = 0.5s = = π δ π 1+ r res,60 = 0.63s = = π δ π 1+ r Nora krutoi je data forulo: N= 1 1 S l + E A s s A s poprečni presjek provodnika S rezultantna opružna konanta za oba nosača u rasponu: za provodnike koji ispoljavaju silu na potporni izolatoria koji se nalaze na nosačia S= N/ Za provodnike na izolatorski lancia: S= N/ do N/ za nazivni napon 110 kv; S= N/ do N/ za nazivni napon 0 kv; S= N/ do N/ za nazivni napon 400 kv. rana 3
4 U zadatku su u pitanju provodnici poavljeni na potporni izolatoria pa se uzia S= N/. E s varni Jungov oduo elaičnoi koji se računa prea relaciji: E F E sin 90 za fin σ δ fin s= F E za > δfin F N δ = fin Zajeno brojnih podataka ia se: - za teperaturu -0ºC: F,-0 400N 6 N = = δ 6 A s ( ) F 73N N = = δ, ( ) 10 Sada je: F,-0 Es, 0 = E sin 90 = σ fin 9 N 400N 10 N = sin 90 = N fin fin F,60 Es,60 = E sin 90 σ = fin 9 N N = sin 90 = N Zajeno u noru krutoi dobija se: N 0 = S l + Es, 0 3 N 10 N = + = N rana 4
5 N60 = S l + Es,60 3 N 10 N = + = N Faktor naprezanja provodnika je dat relacijo: ( g ' ) l ξ= 4 F N 3 ( g ' l) ( ) ξ = = = F, 0 N ( g ' l) ( ) ξ = = = F,60 N oko ili na kraju djelovanja ruje kratkog spoja provodnici u rasponu će oscilovati u odnosu na početni položaj za ugao: k1 k1 δ 1 1 cos 360 za res res δ k= k1 δ1 za > 0.5 res U zadatku je: k1 0.5 = = > res,-0 k1 0.5 = = > res,60 Zajeno brojnih podataka ia se: δ =δ = δ = 70.4 = k, 0 k,60 1 Maksialni ugao otklona provodnika δ u rasponu u odnosu na početni položaj toko ili nakon djelovanja ruje kratkog spoja se računa na sledeći način: rana 5
6 ( ) 1 r sinδk za 0 δk 90 χ= 1 r zaδ k> 90 Zajeno brojnih podataka ia se: χ 0 = χ60 = 1 r= 1.80= 1.80 Sada je δ : 1.5 arccos(χ) za χ 1 δ = 10 + arccos(χ) za χ < zaχ< δ, 0 =δ,60 = 180 Sada se računaju potrebne sile na sljedeći način: Proračun sile zatezanja F t usljed otklona provodnika: Za proračun ove sile računa se prvo paraetar: 3 ( 1+ r 1) za φ = 3 (r sinδ + cosδ 1) za res k1 k k k1 Odnos: res, k1= 0.5 = = res, k1= 0.5 = = odakle se dobija: 4 < 4 res ( ) ϕ 0 =ϕ 60 = 3 ( 1+ r 1) = = Faktor ψ koji je potreban za proračun sile zatezanja usljed otklona provodnika dobija se sa grafika na slici kao funkcija paraetara φ i ξ. U naše slučaju se dobija: rana 6
7 ( ) ( ) ( ) ( ) ψ =ψϕ, ξ =ψ 5.953,.7915= ψ =ψϕ, ξ =ψ 5.953,8.759 = Sada se sila zatezanja usljed otklona provodnika F t ože izračunati po relaciji: t ( ) F= F 1+ϕ ψ ( ) ( ) ( ) ( ) F = F 1+ϕ ψ = = 18.1N t, 0, F = F 1+ϕ ψ = = 1486.N t,60, Veća od ovih sila uzia se kao jerodavna za silu zatezanja usljed otklona provodnika, tj. Ft= 18.1N Proračun sile usljed pada provodnika nakon kratkog spoja F f : Poslije kratkog spoja provodnik osciluje ili pada iz aksialnog otklona prea zelji. Ova sila se razatra u sao u slučaju kad je r>0.6 ako je δ >70. U ovo slučaju ova sila se računa po relaciji: δ Ff = 1. F 1+ 8 ξ 180 U naše slučaju je r=.80 i ugao δ, 0 =δ,60 = 180 što znači da je potrebno izračunati ovu silu: δ, Ff, 0 = 1. F, ξ 0 = = 318.6N δ, Ff,60 = 1. F, ξ60 = = 760.9N rana 7
8 Veća od ovih sila uzia se kao jerodavna za silu usljed pada provodnika nakon kratkog spoja, tj. Ff = 760.9N Konačno, kao jerodavna sila za nosače sa potporni izolatoria bira se veća sila od vrijednoi 1.5 F t i F f tj. F=ax{1.5 F t, F f }= ax{ , 760.9}= = ax{733.1, 760.9}= 760.9N rana 8
ТП 10д Прилог 3
 ЈП ЕЛЕКТРОПРИВРЕДА СРБИЈЕ Београд, Војводе Степе 412 ПРИЛОГ број 3 ТЕХНИЧКЕ ПРЕПОРУКЕ број 10 д ПРИМЕРИ СА КОМЕНТАРОМ МЕХАНИЧКОГ ПРОРАЧУНА ТЕЛЕКОМУНИКАЦИОНИХ КАБЛОВА ЗА ПОСТАВЉАЊЕ ПО СТУБОВИМА ЕЛЕКТРОДИСТРИБУТИВНИХ
ЈП ЕЛЕКТРОПРИВРЕДА СРБИЈЕ Београд, Војводе Степе 412 ПРИЛОГ број 3 ТЕХНИЧКЕ ПРЕПОРУКЕ број 10 д ПРИМЕРИ СА КОМЕНТАРОМ МЕХАНИЧКОГ ПРОРАЧУНА ТЕЛЕКОМУНИКАЦИОНИХ КАБЛОВА ЗА ПОСТАВЉАЊЕ ПО СТУБОВИМА ЕЛЕКТРОДИСТРИБУТИВНИХ
Microsoft Word - TP10v Prilog Deveta varijanta.doc
 ЈП ЕЛЕКТРОПРИВРЕДА СРБИЈЕ Дирекција за дистрибуцију електричне енергије ПРИЛОГ ТЕХНИЧКЕ ПРЕПОРУКЕ број 10 в МЕХАНИЧКИ ПРОРАЧУН СРЕДЊЕНАПОНСКИХ ДИСТРИБУТИВНИХ НАДЗЕМНИХ ВОДОВА ИЗВЕДЕНИХ СЛАБОИЗОЛОВАНИМ
ЈП ЕЛЕКТРОПРИВРЕДА СРБИЈЕ Дирекција за дистрибуцију електричне енергије ПРИЛОГ ТЕХНИЧКЕ ПРЕПОРУКЕ број 10 в МЕХАНИЧКИ ПРОРАЧУН СРЕДЊЕНАПОНСКИХ ДИСТРИБУТИВНИХ НАДЗЕМНИХ ВОДОВА ИЗВЕДЕНИХ СЛАБОИЗОЛОВАНИМ
PRIMER 1 ISPITNI ZADACI 1. ZADATAK Teret težine G = 2 [kn] vezan je užadima DB i DC. Za ravnotežni položaj odrediti sile u užadima. = 60 o, β = 120 o
![PRIMER 1 ISPITNI ZADACI 1. ZADATAK Teret težine G = 2 [kn] vezan je užadima DB i DC. Za ravnotežni položaj odrediti sile u užadima. = 60 o, β = 120 o PRIMER 1 ISPITNI ZADACI 1. ZADATAK Teret težine G = 2 [kn] vezan je užadima DB i DC. Za ravnotežni položaj odrediti sile u užadima. = 60 o, β = 120 o](/thumbs/102/155855156.jpg) PRIMER 1 ISPITNI ZADACI Teret težine G = 2 [kn] vezan je užadima DB i DC. Za ravnotežni položaj odrediti sile u užadima. = 60 o, β = 120 o Homogena pločica ACBD, težine G, sa težištem u tački C, dobijena
PRIMER 1 ISPITNI ZADACI Teret težine G = 2 [kn] vezan je užadima DB i DC. Za ravnotežni položaj odrediti sile u užadima. = 60 o, β = 120 o Homogena pločica ACBD, težine G, sa težištem u tački C, dobijena
Microsoft Word - TPLJ-januar 2017.doc
 Београд, 21. јануар 2017. 1. За дату кружну плочу која је еластично укљештена у кружни прстен и оптерећења према слици одредити максимални напон у кружном прстену. М = 150 knm/m p = 30 kn/m 2 2. За зидни
Београд, 21. јануар 2017. 1. За дату кружну плочу која је еластично укљештена у кружни прстен и оптерећења према слици одредити максимални напон у кружном прстену. М = 150 knm/m p = 30 kn/m 2 2. За зидни
Каталог електроматеријала и опреме ПРИЛОГ Ж. 1 ШИФРА: Двоструки, механички и електрично појачани, затезни изолаторски ланац са штапном изолаторс
 Каталог електроматеријала и опреме ПРИЛОГ Ж. 1 ШИФРА: 30635 Двоструки, механички и електрично појачани, затезни изолаторски ланац са штапном изолаторском јединицом назначеног напона 35kV - "DZp" 35kV,
Каталог електроматеријала и опреме ПРИЛОГ Ж. 1 ШИФРА: 30635 Двоструки, механички и електрично појачани, затезни изолаторски ланац са штапном изолаторском јединицом назначеног напона 35kV - "DZp" 35kV,
ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ
 Универзитет у Београду, Електротехнички факултет, Катедра за енергетске претвараче и погоне ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ (3Е3ЕНТ) Јул 9. Трофазни уљни енергетски трансформатор са номиналним подацима: 4 V,
Универзитет у Београду, Електротехнички факултет, Катедра за енергетске претвараче и погоне ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ (3Е3ЕНТ) Јул 9. Трофазни уљни енергетски трансформатор са номиналним подацима: 4 V,
Slide 1
 Завод за унапређивање образовања и васпитања Аутори: Наставни предмет: MилојеЂурић,професор,Техничка школа Шабац, Марија Пилиповић,професор, Техничка школа Шабац, Александар Ђурић,професор,Мачванска средња
Завод за унапређивање образовања и васпитања Аутори: Наставни предмет: MилојеЂурић,професор,Техничка школа Шабац, Марија Пилиповић,професор, Техничка школа Шабац, Александар Ђурић,професор,Мачванска средња
Microsoft Word - TAcKA i PRAVA3.godina.doc
 TAČKA i PRAVA Najpre ćemo se upoznati sa osnovnim formulama i njihovom primenom.. Rastojanje izmeñu dve tače Ao su nam date tače A( x, y i B( x, y, onda rastojanje izmeñu njih računamo po formuli d( A,
TAČKA i PRAVA Najpre ćemo se upoznati sa osnovnim formulama i njihovom primenom.. Rastojanje izmeñu dve tače Ao su nam date tače A( x, y i B( x, y, onda rastojanje izmeñu njih računamo po formuli d( A,
PowerPoint Presentation
 Keijsko tehnološki fakultet Sveučilišta u Splitu Stručni studij keijske tehnologije i aterijala Stručni studij prehrabene tehnologije Fizika uditorne vježbe 4 Rad i energija. Sudari. Ivica Sorić (Ivica.Soric@fesb.hr)
Keijsko tehnološki fakultet Sveučilišta u Splitu Stručni studij keijske tehnologije i aterijala Stručni studij prehrabene tehnologije Fizika uditorne vježbe 4 Rad i energija. Sudari. Ivica Sorić (Ivica.Soric@fesb.hr)
Pismeni ispit iz MEHANIKE MATERIJALA I - grupa A 1. Kruta poluga AB, oslonjena na oprugu BC i okačena o uže BD, nosi kontinuirano opterećenje, kao što
 Pismeni ispit iz MEHNIKE MTERIJL I - grupa 1. Kruta poluga, oslonjena na oprugu i okačena o uže D, nosi kontinuirano opterećenje, kao što je prikazano na slici desno. Odrediti: a) silu i napon u užetu
Pismeni ispit iz MEHNIKE MTERIJL I - grupa 1. Kruta poluga, oslonjena na oprugu i okačena o uže D, nosi kontinuirano opterećenje, kao što je prikazano na slici desno. Odrediti: a) silu i napon u užetu
Microsoft Word - Elektrijada_2008.doc
 I област. У колу сталне струје са слике познато је: а) када је E, E = и E = укупна снага 3 отпорника је P = W, б) када је E =, E и E = укупна снага отпорника је P = 4 W и 3 в) када је E =, E = и E укупна
I област. У колу сталне струје са слике познато је: а) када је E, E = и E = укупна снага 3 отпорника је P = W, б) када је E =, E и E = укупна снага отпорника је P = 4 W и 3 в) када је E =, E = и E укупна
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА школска 2017/2018. година ТЕС
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА школска 017/018. година ТЕСТ ФИЗИКА ПРИЈЕМНИ ИСПИТ ЗА УПИС УЧЕНИКА СА ПОСЕБНИМ СПОСОБНОСТИМА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА школска 017/018. година ТЕСТ ФИЗИКА ПРИЈЕМНИ ИСПИТ ЗА УПИС УЧЕНИКА СА ПОСЕБНИМ СПОСОБНОСТИМА
ЕНЕРГЕТСКИ ПРЕТВАРАЧИ септембар 2005
 ЕНЕРГЕТСКИ ПРЕТВАРАЧИ 1 фебруар 1. год. 1. Пећ сачињена од три грејача отпорности R=6Ω, везана у звезду, напаја се са мреже xv, 5Hz, преко три фазна регулатора, као на слици. Угао "паљења" тиристора је
ЕНЕРГЕТСКИ ПРЕТВАРАЧИ 1 фебруар 1. год. 1. Пећ сачињена од три грејача отпорности R=6Ω, везана у звезду, напаја се са мреже xv, 5Hz, преко три фазна регулатора, као на слици. Угао "паљења" тиристора је
Predavanje 8-TEMELJI I POTPORNI ZIDOVI.ppt
 1 BETONSKE KONSTRUKCIJE TEMELJI OBJEKATA Prof. dr Snežana Marinković Doc. dr Ivan Ignjatović Semestar: V ESPB: Temelji objekata 2 1.1. Podela 1.2. Temelji samci 1.3. Temeljne trake 1.4. Temeljne grede
1 BETONSKE KONSTRUKCIJE TEMELJI OBJEKATA Prof. dr Snežana Marinković Doc. dr Ivan Ignjatović Semestar: V ESPB: Temelji objekata 2 1.1. Podela 1.2. Temelji samci 1.3. Temeljne trake 1.4. Temeljne grede
9. : , ( )
 9. Динамика тачке: Енергиjа, рад и снага (први део) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj - Шта ћемо научити (1) 1. Преглед литературе
9. Динамика тачке: Енергиjа, рад и снага (први део) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj - Шта ћемо научити (1) 1. Преглед литературе
48. РЕПУБЛИЧКО ТАКМИЧЕЊЕ ИЗ ФИЗИКЕ УЧЕНИКА СРЕДЊИХ ШКОЛА ШКОЛСКЕ 2009/2010. ГОДИНЕ I РАЗРЕД Друштво Физичара Србије Министарство Просвете Републике Ср
 I РАЗРЕД Друштво Физичара Србије Министарство Просвете Републике Србије ЗАДАЦИ ГИМНАЗИЈА ВЕЉКО ПЕТРОВИЋ СОМБОР 7.0.00.. На слици је приказана шема електричног кола. Електромоторна сила извора је ε = 50
I РАЗРЕД Друштво Физичара Србије Министарство Просвете Републике Србије ЗАДАЦИ ГИМНАЗИЈА ВЕЉКО ПЕТРОВИЋ СОМБОР 7.0.00.. На слици је приказана шема електричног кола. Електромоторна сила извора је ε = 50
Microsoft Word - AM_SM_Samostalni_Rad.doc
 OG2EM Zadaci za saostalni u toku druge polovine kursa Tekst sadrži 1 zadataka koji predstavljaju varijaciju zadataka rađenih u toku časova računskih vežbi. Izenjene su brojne vrednosti, ni režii, i slično.
OG2EM Zadaci za saostalni u toku druge polovine kursa Tekst sadrži 1 zadataka koji predstavljaju varijaciju zadataka rađenih u toku časova računskih vežbi. Izenjene su brojne vrednosti, ni režii, i slično.
ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ
 Универзитет у Београду Електротехнички факултет Катедра за енергетске претвараче и погоне ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ (ЕЕНТ) Фебруар 8. Трофазни уљни енергетски трансформатор са номиналним подацима: S =
Универзитет у Београду Електротехнички факултет Катедра за енергетске претвараче и погоне ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ (ЕЕНТ) Фебруар 8. Трофазни уљни енергетски трансформатор са номиналним подацима: S =
Динамика крутог тела
 Динамика крутог тела. Задаци за вежбу 1. Штап масе m и дужине L се крајем А наслања на храпаву хоризонталну раван, док на другом крају дејствује сила F константног интензитета и правца нормалног на штап.
Динамика крутог тела. Задаци за вежбу 1. Штап масе m и дужине L се крајем А наслања на храпаву хоризонталну раван, док на другом крају дејствује сила F константног интензитета и правца нормалног на штап.
ТЕСТ ИЗ ФИЗИКЕ ИМЕ И ПРЕЗИМЕ 1. У основне величине у физици, по Међународном систему јединица, спадају и следеће три величине : а) маса, температура,
 ТЕСТ ИЗ ФИЗИКЕ ИМЕ И ПРЕЗИМЕ 1. У основне величине у физици, по Међународном систему јединица, спадају и следеће три величине : а) маса, температура, електрични отпор б) сила, запремина, дужина г) маса,
ТЕСТ ИЗ ФИЗИКЕ ИМЕ И ПРЕЗИМЕ 1. У основне величине у физици, по Међународном систему јединица, спадају и следеће три величине : а) маса, температура, електрични отпор б) сила, запремина, дужина г) маса,
ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 2006/2007 године I разред
 ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 006/007 године разред. Електрични систем се састоји из отпорника повезаних тако
ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 006/007 године разред. Електрични систем се састоји из отпорника повезаних тако
Rucka.dft
 Средња машинска школа РАДОЈЕ ДАКИЋ АУТОДИЗАЛИЦА ТАРА Милош Мајсторовић Средња машинска Прорачун: школа Аутодизалице " Тара " Пројекат РАДОЈЕ ДАКИЋ Лист ПРОРАЧУН НОСИВОСТИ АУТОДИЗАЛИЦЕ " ТАРА " ПОДАЦИ:
Средња машинска школа РАДОЈЕ ДАКИЋ АУТОДИЗАЛИЦА ТАРА Милош Мајсторовић Средња машинска Прорачун: школа Аутодизалице " Тара " Пројекат РАДОЈЕ ДАКИЋ Лист ПРОРАЧУН НОСИВОСТИ АУТОДИЗАЛИЦЕ " ТАРА " ПОДАЦИ:
ma??? - Primer 1 Spregnuta ploca
 Primer 1 - proračun spregnute ploče na profilisanom limu 1. Karakteristike spregnute ploče Spregnuta ploča je raspona 4 m. Predviđen je jedan privremeni oslonac u polovini raspona ploče u toku građenja.
Primer 1 - proračun spregnute ploče na profilisanom limu 1. Karakteristike spregnute ploče Spregnuta ploča je raspona 4 m. Predviđen je jedan privremeni oslonac u polovini raspona ploče u toku građenja.
Microsoft Word - Elektrijada_V2_2014_final.doc
 I област. У колу сталне струје са слике када је и = V, амперметар показује I =. Одредити показивање амперметра I када је = 3V и = 4,5V. Решење: а) I = ) I =,5 c) I =,5 d) I = 7,5 3 3 Слика. I област. Дата
I област. У колу сталне струје са слике када је и = V, амперметар показује I =. Одредити показивање амперметра I када је = 3V и = 4,5V. Решење: а) I = ) I =,5 c) I =,5 d) I = 7,5 3 3 Слика. I област. Дата
Analiticka geometrija
 Analitička geometrija Predavanje 4 Ekscentricitet konusnih preseka i klasifikacija kvadratnih krivih Novi Sad, 2018. Milica Žigić (PMF, UNS 2018) Analitička geometrija predavanje 4 1 / 15 Ekscentricitet
Analitička geometrija Predavanje 4 Ekscentricitet konusnih preseka i klasifikacija kvadratnih krivih Novi Sad, 2018. Milica Žigić (PMF, UNS 2018) Analitička geometrija predavanje 4 1 / 15 Ekscentricitet
Microsoft PowerPoint - ME_P1-Uvodno predavanje [Compatibility Mode]
![Microsoft PowerPoint - ME_P1-Uvodno predavanje [Compatibility Mode] Microsoft PowerPoint - ME_P1-Uvodno predavanje [Compatibility Mode]](/thumbs/103/157430298.jpg) MAŠINSKI ELEMENTI dr Miloš Ristić UVOD Mašinski elementi predstavljaju tehničkonaučnu disciplinu. Izučavanjem ove discipline stiču seteorijska i praktična znanja za proračun, izbor i primenu mašinskih
MAŠINSKI ELEMENTI dr Miloš Ristić UVOD Mašinski elementi predstavljaju tehničkonaučnu disciplinu. Izučavanjem ove discipline stiču seteorijska i praktična znanja za proračun, izbor i primenu mašinskih
ЕНЕРГЕТСКИ ПРЕТВАРАЧИ септембар 2005
 ЕНЕРГЕТСКИ ПРЕТВАРАЧИ јануар 0. год.. Потрошач чија је привидна снага S =500kVA и фактор снаге cosφ=0.8 (индуктивно) прикључен је на мрежу 3x380V, 50Hz. У циљу компензације реактивне снаге, паралелно са
ЕНЕРГЕТСКИ ПРЕТВАРАЧИ јануар 0. год.. Потрошач чија је привидна снага S =500kVA и фактор снаге cosφ=0.8 (индуктивно) прикључен је на мрежу 3x380V, 50Hz. У циљу компензације реактивне снаге, паралелно са
ЕНЕРГЕТСКИ ПРЕТВАРАЧИ септембар 2005
 ЕНЕРГЕТСКИ ПРЕТВАРАЧИ јануар 00. год.. Пећ сачињена од три грејача отпорности =0Ω, везана у звезду, напаја се са мреже 3x380V, 50Hz, преко три фазна регулатора, као на слици. Угао паљења тиристора је α=90,
ЕНЕРГЕТСКИ ПРЕТВАРАЧИ јануар 00. год.. Пећ сачињена од три грејача отпорности =0Ω, везана у звезду, напаја се са мреже 3x380V, 50Hz, преко три фазна регулатора, као на слици. Угао паљења тиристора је α=90,
Univerzitet u Beogradu Elektrotehnički fakultet Katedra za energetske pretvarače i pogone ISPIT IZ SINHRONIH MAŠINA (13E013SIM) 1. Poznati su podaci o
 Univerzitet u Beogradu Elektrotehnički akultet Katedra za energetske pretvarače i pogone ISPIT IZ SINHRONIH MAŠINA (13E013SIM) 1. Poznati su podaci o namotaju statora sinhronog motora sa stalnim magnetima
Univerzitet u Beogradu Elektrotehnički akultet Katedra za energetske pretvarače i pogone ISPIT IZ SINHRONIH MAŠINA (13E013SIM) 1. Poznati su podaci o namotaju statora sinhronog motora sa stalnim magnetima
Microsoft Word - ETH2_EM_Amperov i generalisani Amperov zakon - za sajt
 Полупречник унутрашњег проводника коаксијалног кабла је Спољашњи проводник је коначне дебљине унутрашњег полупречника и спољашњег Проводници кабла су начињени од бакра Кроз кабл протиче стална једносмерна
Полупречник унутрашњег проводника коаксијалног кабла је Спољашњи проводник је коначне дебљине унутрашњег полупречника и спољашњег Проводници кабла су начињени од бакра Кроз кабл протиче стална једносмерна
Slide 1
 Анализа електроенергетских система -Прорачун кратких спојева- Кратак спој представља поремећено стање мреже, односно поремећено стање система. За време трајања кратког споја напони и струје се мењају са
Анализа електроенергетских система -Прорачун кратких спојева- Кратак спој представља поремећено стање мреже, односно поремећено стање система. За време трајања кратког споја напони и струје се мењају са
Rešetkasti nosači
 Elementi opterećeni savijanjem - nosači Metalne konstrukcije 1 P6-1 Slučajevi naprezanja Savijanje dominantan vid naprezanja! Savijanje može biti posledica sledećih naprezanja: čisto pravo savijanje (M
Elementi opterećeni savijanjem - nosači Metalne konstrukcije 1 P6-1 Slučajevi naprezanja Savijanje dominantan vid naprezanja! Savijanje može biti posledica sledećih naprezanja: čisto pravo savijanje (M
5 - gredni sistemi
 Гредни системи бетонских мостова 1 БЕТОНСКИ МОСТОВИ ГРЕДНИ СИСТЕМИ Типови гредних система бетонских мостова Решетка Проста греда Греда с препустима Герберова греда Континуална греда Укљештена греда 2 Трајекторије
Гредни системи бетонских мостова 1 БЕТОНСКИ МОСТОВИ ГРЕДНИ СИСТЕМИ Типови гредних система бетонских мостова Решетка Проста греда Греда с препустима Герберова греда Континуална греда Укљештена греда 2 Трајекторије
mfb_jun_2018_res.dvi
 Универзитет у Београду Машински факултет Катедра за механику флуида МЕХАНИКА ФЛУИДА Б Писмени део испита Име и презиме:... Броj индекса:... Смена:... Напомене: Испит траjе 80 минута. Коришћење литературе
Универзитет у Београду Машински факултет Катедра за механику флуида МЕХАНИКА ФЛУИДА Б Писмени део испита Име и презиме:... Броj индекса:... Смена:... Напомене: Испит траjе 80 минута. Коришћење литературе
Microsoft PowerPoint - predavanje_sile_primena_2013
 Примене Њутнових закона Претпоставке Објекти представљени материјалном тачком занемарите ротацију (за сада) Масе конопаца су занемариве Заинтересовани смо само за силе које делују на објекат можемо да
Примене Њутнових закона Претпоставке Објекти представљени материјалном тачком занемарите ротацију (за сада) Масе конопаца су занемариве Заинтересовани смо само за силе које делују на објекат можемо да
Каталог електроматеријала и опреме ПРИЛОГ В. 16 ШИФРА: 2670 Р.бр. Опис јм Захтевано Понуђено 1. ОПШТЕ 1.1. Произвођач 1.2. Тип Трополни растављач 12 k
 Каталог електроматеријала и опреме ПРИЛОГ В. 16 ШИФРА: 2670 1.1. Произвођач Трополни растављач 12, MRT 12-630/75-210 или еквивалентан За унутрашњу монтажу Називни напон мреже 10 За чеону монтажу,сигналном
Каталог електроматеријала и опреме ПРИЛОГ В. 16 ШИФРА: 2670 1.1. Произвођач Трополни растављач 12, MRT 12-630/75-210 или еквивалентан За унутрашњу монтажу Називни напон мреже 10 За чеону монтажу,сигналном
Mister Door d.o.o. Bul. Despota Stefana Beograd tel/fax: 011/ mob: 069/ web: Cenovnik S
 Model C50 - ontaža na pod Donji nosači sa asko, Staklo kaljeni Panplex 88.2, bez rukohvata Visina Stakla = Visina ograde - 3c Nosač 40.00 /ko 3 ko 120.00 Maksialna širina stakla = 120c Unutr. Poklopac
Model C50 - ontaža na pod Donji nosači sa asko, Staklo kaljeni Panplex 88.2, bez rukohvata Visina Stakla = Visina ograde - 3c Nosač 40.00 /ko 3 ko 120.00 Maksialna širina stakla = 120c Unutr. Poklopac
Прикључење објекта произвођача Тачке као и тачке , и у постојећим Правилима о раду дистрибутивно
 Прикључење објекта произвођача Тачке 3.5.1. 3.5.6. као и тачке 3.5.7.14.6.1, 3.5.7.14.6.3. и 3.5.7.14.6.5. у постојећим Правилима о раду дистрибутивног система се мењају са оним које су наведене у тексту
Прикључење објекта произвођача Тачке 3.5.1. 3.5.6. као и тачке 3.5.7.14.6.1, 3.5.7.14.6.3. и 3.5.7.14.6.5. у постојећим Правилима о раду дистрибутивног система се мењају са оним које су наведене у тексту
Математика напредни ниво 1. Посматрај слике, па поред тачног тврђења стави слово Т, а поред нетачног Н. а) A B б) C D в) F E г) G F д) E F ђ) D C 2. О
 1. Посматрај слике, па поред тачног тврђења стави слово Т, а поред нетачног Н. а) A B б) C D в) F E г) G F д) E F ђ) D C 2. Одреди број елемената скупова: а) A = {x x N и x < 5} A = { } n(a) = б) B = {x
1. Посматрај слике, па поред тачног тврђења стави слово Т, а поред нетачног Н. а) A B б) C D в) F E г) G F д) E F ђ) D C 2. Одреди број елемената скупова: а) A = {x x N и x < 5} A = { } n(a) = б) B = {x
Microsoft Word - Domacii zadatak Vektori i analiticka geometrija OK.doc
 задатак. Вектор написати као линеарну комбинацију вектора.. }. } } }. }. } } }. }. } } }. }. } } 9}. }. } } }. }. } } }. }. } } } 9 8. }. } } } 9. }. } } }. }. } } }. }. } } }. }. } } }. }. } } }. }. }
задатак. Вектор написати као линеарну комбинацију вектора.. }. } } }. }. } } }. }. } } }. }. } } 9}. }. } } }. }. } } }. }. } } } 9 8. }. } } } 9. }. } } }. }. } } }. }. } } }. }. } } }. }. } } }. }. }
Microsoft Word - 4.Ee1.AC-DC_pretvaraci.10
 AC-DC ПРЕТВАРАЧИ (ИСПРАВЉАЧИ) Задатак 1. Једнофазни исправљач са повратном диодом, са слике 1, прикључен на напон 1 V, 5 Hz напаја потрошач велике индуктивности струјом од 1 А. Нацртати таласне облике
AC-DC ПРЕТВАРАЧИ (ИСПРАВЉАЧИ) Задатак 1. Једнофазни исправљач са повратном диодом, са слике 1, прикључен на напон 1 V, 5 Hz напаја потрошач велике индуктивности струјом од 1 А. Нацртати таласне облике
EНЕРГЕТСКИ ПРЕТВАРАЧИ 1 јануар Трофазни једнострани исправљач прикључен је на круту мрежу 3x380V, 50Hz преко трансформатора у спрези Dy, као
 EНЕРГЕТСКИ ПРЕТВАРАЧИ 1 јануар 017. 1. Трофазни једнострани исправљач прикључен је на круту мрежу x80, 50Hz преко трансформатора у спрези Dy, као на слици 1. У циљу компензације реактивне снаге, паралелно
EНЕРГЕТСКИ ПРЕТВАРАЧИ 1 јануар 017. 1. Трофазни једнострани исправљач прикључен је на круту мрежу x80, 50Hz преко трансформатора у спрези Dy, као на слици 1. У циљу компензације реактивне снаге, паралелно
6. TEHNIČKE MJERE SIGURNOSTI U IZVEDBI ELEKTROENERGETSKIH VODOVA
 SIGURNOST U PRIMJENI ELEKTRIČNE ENERGIJE 6. TEHNIČKE MJERE SIGURNOSTI U IZVEDBI ELEKTROENERGETSKIH VODOVA Izv.prof. dr.sc. Vitomir Komen, dipl.ing.el. 1/14 SADRŽAJ: 6.1 Sigurnosni razmaci i sigurnosne
SIGURNOST U PRIMJENI ELEKTRIČNE ENERGIJE 6. TEHNIČKE MJERE SIGURNOSTI U IZVEDBI ELEKTROENERGETSKIH VODOVA Izv.prof. dr.sc. Vitomir Komen, dipl.ing.el. 1/14 SADRŽAJ: 6.1 Sigurnosni razmaci i sigurnosne
Slide 1
 Грађевински факултет Универзитета у Београду МОСТОВИ Субструктура моста Вежбе 4 Програм предмета Датум бч. Предавања бч. Вежбе 1 22.02. 4 Уводно предавање - 2 01.03. 3 Дефиниције, системи, распони и материјали
Грађевински факултет Универзитета у Београду МОСТОВИ Субструктура моста Вежбе 4 Програм предмета Датум бч. Предавања бч. Вежбе 1 22.02. 4 Уводно предавање - 2 01.03. 3 Дефиниције, системи, распони и материјали
1. Vrednost izraza jednaka je: Rexenje Direktnim raqunom dobija se = 4 9, ili kra e S = 1 ( 1 1
 1. Vrednost izraza 1 1 + 1 5 + 1 5 7 + 1 7 9 jednaka je: Rexenje Direktnim raqunom dobija se 1 + 1 15 + 1 5 + 1 6 = 4 9, ili kra e S = 1 1 1 2 + 1 1 5 + 1 5 1 7 + 1 7 1 ) = 1 7 2 8 9 = 4 9. 2. Ako je fx)
1. Vrednost izraza 1 1 + 1 5 + 1 5 7 + 1 7 9 jednaka je: Rexenje Direktnim raqunom dobija se 1 + 1 15 + 1 5 + 1 6 = 4 9, ili kra e S = 1 1 1 2 + 1 1 5 + 1 5 1 7 + 1 7 1 ) = 1 7 2 8 9 = 4 9. 2. Ako je fx)
III разред ТАКМИЧЕЊЕ ИЗ ФИЗИКЕ УЧЕНИКА СРЕДЊИХ ШКОЛА ШКОЛСКА 2018/19. ГОДИНА Друштво физичара Србиjе и Министарство просвете, науке и технолошког разв
 ЗАДАЦИ ФЕРМИОНСКА КАТЕГОРИJА 1. Маjа се пење уз покретне степенице под углом од θ = 30 и дужине L = 10m. Ако jе линеарна брзина степеница v S = m s, а она се у односу на њих креће брзином v M = 1, m s,
ЗАДАЦИ ФЕРМИОНСКА КАТЕГОРИJА 1. Маjа се пење уз покретне степенице под углом од θ = 30 и дужине L = 10m. Ако jе линеарна брзина степеница v S = m s, а она се у односу на њих креће брзином v M = 1, m s,
Proračun i konstruisanje veza pod uglom
 Momentne veze Metalne konstrukcije 2 P5-1 Karekteristike momentnih veza Sposobne su da prenesu i momente savijanja; U ovu kategoriju spadaju: krute i polu-krute, odnosno potpuno ili delimično nosive veze;
Momentne veze Metalne konstrukcije 2 P5-1 Karekteristike momentnih veza Sposobne su da prenesu i momente savijanja; U ovu kategoriju spadaju: krute i polu-krute, odnosno potpuno ili delimično nosive veze;
III разред ТАКМИЧЕЊЕ ИЗ ФИЗИКЕ УЧЕНИКА СРЕДЊИХ ШКОЛА ШКОЛСКА 2018/19. ГОДИНА Друштво физичара Србиjе и Министарство просвете, науке и технолошког разв
 ЗАДАЦИ БОЗОНСКА КАТЕГОРИJА 1. Деjан и Jован играjу кошарку за два различита кошаркашка клуба. У току утакмице, Деjан шутира троjку са удаљености D = 7,5 m. Након што подигне руке при избачаjу, лопта jе
ЗАДАЦИ БОЗОНСКА КАТЕГОРИJА 1. Деjан и Jован играjу кошарку за два различита кошаркашка клуба. У току утакмице, Деjан шутира троjку са удаљености D = 7,5 m. Након што подигне руке при избачаjу, лопта jе
Proracun strukture letelica - Vežbe 6
 University of Belgrade Faculty of Mechanical Engineering Proračun strukture letelica Vežbe 6 15.4.2019. Mašinski fakultet Univerziteta u Beogradu Danilo M. Petrašinović Jelena M. Svorcan Miloš D. Petrašinović
University of Belgrade Faculty of Mechanical Engineering Proračun strukture letelica Vežbe 6 15.4.2019. Mašinski fakultet Univerziteta u Beogradu Danilo M. Petrašinović Jelena M. Svorcan Miloš D. Petrašinović
Sinhrone mašine Namotaji sinhronih mašina, reakcija indukta, reaktansa namotaja 27. februar 2019.
 Sinhrone mašine Namotaji sinhronih mašina, reakcija indukta, reaktansa namotaja 7. februar 019. Podsetnik osnovne veličine namotaja Nomenklatura: Q....................... p........................ q........................
Sinhrone mašine Namotaji sinhronih mašina, reakcija indukta, reaktansa namotaja 7. februar 019. Podsetnik osnovne veličine namotaja Nomenklatura: Q....................... p........................ q........................
Sveučilište J.J. Strossmayera Fizika 2 FERIT Predložak za laboratorijske vježbe Cilj vježbe Određivanje specifičnog naboja elektrona Odrediti specifič
 Cilj vježbe Određivanje specifičnog naboja elektrona Odrediti specifični naboja elektrona (omjer e/me) iz poznatog polumjera putanje elektronske zrake u elektronskoj cijevi, i poznatog napona i jakosti
Cilj vježbe Određivanje specifičnog naboja elektrona Odrediti specifični naboja elektrona (omjer e/me) iz poznatog polumjera putanje elektronske zrake u elektronskoj cijevi, i poznatog napona i jakosti
mfb_april_2018_res.dvi
 Универзитет у Београду Машински факултет Катедра за механику флуида МЕХАНИКА ФЛУИДА Б Писмени део испита Име и презиме:... Броj индекса:... Напомене: Испит траjе 80 минута. Коришћење литературе ниjе дозвољено!
Универзитет у Београду Машински факултет Катедра за механику флуида МЕХАНИКА ФЛУИДА Б Писмени део испита Име и презиме:... Броj индекса:... Напомене: Испит траjе 80 минута. Коришћење литературе ниjе дозвољено!
PRIRODNO-MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA MATEMATIKU I INFORMATIKU ZADACI SA REŠENJIMA SA PRIJEMNOG ISPITA IZ MATEMATIKE, JUN Odrediti
 PRIRODNO-MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA MATEMATIKU I INFORMATIKU ZADACI SA REŠENJIMA SA PRIJEMNOG ISPITA IZ MATEMATIKE, JUN 0. Odrediti moduo kompleksnog broja Rešenje: Uočimo da važi z = + i00
PRIRODNO-MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA MATEMATIKU I INFORMATIKU ZADACI SA REŠENJIMA SA PRIJEMNOG ISPITA IZ MATEMATIKE, JUN 0. Odrediti moduo kompleksnog broja Rešenje: Uočimo da važi z = + i00
Microsoft PowerPoint - fizika 9-oscilacije
 Предиспитне обавезе Шема прикупљања поена - измене Активност у току предавања = 5 поена (са више од 3 одсуствовања са предавања се не могу добити) Лабораторијске вежбе = 10 поена обавезни сви поени односно
Предиспитне обавезе Шема прикупљања поена - измене Активност у току предавања = 5 поена (са више од 3 одсуствовања са предавања се не могу добити) Лабораторијске вежбе = 10 поена обавезни сви поени односно
PowerPoint Presentation
 Анализа електроенергетских система -основни прорачуни- Падови напона и губици преноса δu, попречна компонента пада напона Δ U, попречна компонента пада напона U 1 U = Z I = R + jx Icosφ jisinφ = RIcosφ
Анализа електроенергетских система -основни прорачуни- Падови напона и губици преноса δu, попречна компонента пада напона Δ U, попречна компонента пада напона U 1 U = Z I = R + jx Icosφ jisinφ = RIcosφ
Microsoft Word - Resenja_ racunskih_vezbi_emp_mjss_2012.doc
 ELEKTRIČNE MAŠINE Rešenja računskih vežbi PRVI DEO 1 zadatak a) U provodniku koji se kreće u hoogeno agnetno polju postoji elektrootorna sila koja se ože izraziti kao skalarni proizvod vektora dužine provodnika
ELEKTRIČNE MAŠINE Rešenja računskih vežbi PRVI DEO 1 zadatak a) U provodniku koji se kreće u hoogeno agnetno polju postoji elektrootorna sila koja se ože izraziti kao skalarni proizvod vektora dužine provodnika
PowerPoint Presentation
 Анализа електроенергетских система -Временска промена струје кратког споја- Апериодична компонента (брзо се пригушује са T а, реда 5-1 ms, зависи од карактеристика ЕЕС-а и локације квара) Синусоидална
Анализа електроенергетских система -Временска промена струје кратког споја- Апериодична компонента (брзо се пригушује са T а, реда 5-1 ms, зависи од карактеристика ЕЕС-а и локације квара) Синусоидална
АНАЛИЗА ПРОБЛЕМА ТЕРМИЧКЕ ДИЛАТАЦИЈЕ L КОМПЕНЗАТОРА ПРЕМА СТАНДАРДУ AD 2000 И ДРУГИМ МЕТОДАМА Милан Травица Иновациони центар Машински факултет Универ
 АНАЛИЗА ПРОБЛЕМА ТЕРМИЧКЕ ДИЛАТАЦИЈЕ L КОМПЕНЗАТОРА ПРЕМА СТАНДАРДУ AD 2000 И ДРУГИМ МЕТОДАМА Милан Травица Иновациони центар Машински факултет Универзитет у Београду Краљице Марије 16, 11000 Београд mtravica@mas.bg.ac.rs
АНАЛИЗА ПРОБЛЕМА ТЕРМИЧКЕ ДИЛАТАЦИЈЕ L КОМПЕНЗАТОРА ПРЕМА СТАНДАРДУ AD 2000 И ДРУГИМ МЕТОДАМА Милан Травица Иновациони центар Машински факултет Универзитет у Београду Краљице Марије 16, 11000 Београд mtravica@mas.bg.ac.rs
18 1 DERIVACIJA 1.3 Derivacije višeg reda n-tu derivaciju funkcije f označavamo s f (n) ili u Leibnizovoj notaciji s dn y d x n. Zadatak 1.22 Nadite f
 8 DERIVACIJA.3 Derivacije višeg reda n-tu derivaciju funcije f označavamo s f (n) ili u Leibnizovoj notaciji s dn y d x n. Zadata. Nadite f (x) ao je (a) f(x) = ( + x ) arctg x (b) f(x) = e x cos x (a)
8 DERIVACIJA.3 Derivacije višeg reda n-tu derivaciju funcije f označavamo s f (n) ili u Leibnizovoj notaciji s dn y d x n. Zadata. Nadite f (x) ao je (a) f(x) = ( + x ) arctg x (b) f(x) = e x cos x (a)
ЛИНЕАРНА ФУНКЦИЈА ЛИНЕАРНА ФУНКЦИЈА у = kх + n А утврди 1. Које од наведених функција су линеарне: а) у = 2х; б) у = 4х; в) у = 2х 7; г) у = 2 5 x; д)
 ЛИНЕАРНА ФУНКЦИЈА ЛИНЕАРНА ФУНКЦИЈА у = kх + n А утврди 1. Које од наведених функција су линеарне: а) у = х; б) у = 4х; в) у = х 7; г) у = 5 x; д) у = 5x ; ђ) у = х + х; е) у = x + 5; ж) у = 5 x ; з) у
ЛИНЕАРНА ФУНКЦИЈА ЛИНЕАРНА ФУНКЦИЈА у = kх + n А утврди 1. Које од наведених функција су линеарне: а) у = х; б) у = 4х; в) у = х 7; г) у = 5 x; д) у = 5x ; ђ) у = х + х; е) у = x + 5; ж) у = 5 x ; з) у
broj 087_Layout 1
 СЛУЖБЕНИ ГЛАСНИК Језик српског народа ЈУ Службени гласник Републике Српске, Бања Лука, Вељка Млађеновића бб Телефон/факс: (051) 456-331, 456-341 E-mail: slglasnikrs@blic.net slgl.finanse@blic.net slgl.oglasi@blic.net
СЛУЖБЕНИ ГЛАСНИК Језик српског народа ЈУ Службени гласник Републике Српске, Бања Лука, Вељка Млађеновића бб Телефон/факс: (051) 456-331, 456-341 E-mail: slglasnikrs@blic.net slgl.finanse@blic.net slgl.oglasi@blic.net
Зборник радова 6. Међународне конференције о настави физике у средњим школама, Алексинац, март Одређивање коефицијента пригушења у ваздуху
 Одређивање коефицијента пригушења у ваздуху помоћу линеарног хармонијског осцилатора Соња Ковачевић 1, Милан С. Ковачевић 2 1 Прва крагујевачка гимназија, Крагујевац, Србија 2 Природно-математички факултет,
Одређивање коефицијента пригушења у ваздуху помоћу линеарног хармонијског осцилатора Соња Ковачевић 1, Милан С. Ковачевић 2 1 Прва крагујевачка гимназија, Крагујевац, Србија 2 Природно-математички факултет,
Rešetkasti nosači
 Kombinovana naprezanja etalne konstrukcije 1 P8-1 Kontrole graničnih stanja kod kombinovanih naprezanja Ekscentrično zatezanje ( t + ) ULS - kontrole nosivosti poprečnih preseka na pojedinačna dejstva
Kombinovana naprezanja etalne konstrukcije 1 P8-1 Kontrole graničnih stanja kod kombinovanih naprezanja Ekscentrično zatezanje ( t + ) ULS - kontrole nosivosti poprečnih preseka na pojedinačna dejstva
(Microsoft Word doma\346a zada\346a)
 1. Napišite (u sva tri oblika: eksplicitnom, implicitnom i segmentnom) jednadžbu tangente i jednadžbu normale povučene na graf funkcije f u točki T, te izračunajte njihove duljine (s točnošću od 10 5 )
1. Napišite (u sva tri oblika: eksplicitnom, implicitnom i segmentnom) jednadžbu tangente i jednadžbu normale povučene na graf funkcije f u točki T, te izračunajte njihove duljine (s točnošću od 10 5 )
Matematka 1 Zadaci za vežbe Oktobar Uvod 1.1. Izračunati vrednost izraza (bez upotrebe pomoćnih sredstava): ( ) [ a) : b) 3 3
 Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
Microsoft PowerPoint - Teorija kretanja vozila-predavanje 3.1.ppt
 ТЕОРИЈА КРЕТАЊА ВОЗИЛА Предавање. гусенична возила, површински притисак ослањања, гусеница на подлогу ослањања G=mg p p гусеница на подлогу ослањања G=mg средњи стварни p тврда подлога средњи стварни p
ТЕОРИЈА КРЕТАЊА ВОЗИЛА Предавање. гусенична возила, површински притисак ослањања, гусеница на подлогу ослањања G=mg p p гусеница на подлогу ослањања G=mg средњи стварни p тврда подлога средњи стварни p
Матрична анализа конструкција
 . 5 ПРИМЕР На слици. је приказан носач који је састављен од три штапа. Хоризонтални штапови су константног попречног пресека b/h=./.5 m, док је коси штап са линеарном променом висине. Одредити силе на
. 5 ПРИМЕР На слици. је приказан носач који је састављен од три штапа. Хоризонтални штапови су константног попречног пресека b/h=./.5 m, док је коси штап са линеарном променом висине. Одредити силе на
Microsoft Word - Molekuli-zadaci.doc
 Задаци Други колоквијум - Молекулски спектри Пример 1 Израчунајте апсорбанцију раствора, ако је познато да је транспаренција 89% на 00 nm. А 0,071 λ 00 nm таласна дужина на којој је мерена апсорбанција
Задаци Други колоквијум - Молекулски спектри Пример 1 Израчунајте апсорбанцију раствора, ако је познато да је транспаренција 89% на 00 nm. А 0,071 λ 00 nm таласна дужина на којој је мерена апсорбанција
ma??? - Primer 6 Proracun spregnute veze
 Primer 6 Proračun spregnute veze Odrediti proračunski moment nosivosti spregnute veze grede i stuba prikazane na skici. Stub je izrađen od vrućevaljanog profila HEA400, a greda od IPE500. Veza je ostvarena
Primer 6 Proračun spregnute veze Odrediti proračunski moment nosivosti spregnute veze grede i stuba prikazane na skici. Stub je izrađen od vrućevaljanog profila HEA400, a greda od IPE500. Veza je ostvarena
Microsoft Word - 6ms001
 Zadatak 001 (Anela, ekonomska škola) Riješi sustav jednadžbi: 5 z = 0 + + z = 14 4 + + z = 16 Rješenje 001 Sustav rješavamo Gaussovom metodom eliminacije (isključivanja). Gaussova metoda provodi se pomoću
Zadatak 001 (Anela, ekonomska škola) Riješi sustav jednadžbi: 5 z = 0 + + z = 14 4 + + z = 16 Rješenje 001 Sustav rješavamo Gaussovom metodom eliminacije (isključivanja). Gaussova metoda provodi se pomoću
Microsoft PowerPoint - fizika2-kinematika2012
 ФИЗИКА 1. Понедељак, 8. октобар, 1. Кинематика тачке у једној димензији Кинематикакретањаудведимензије 1 Кинематика кретање свејеустањукретања кретање промена положаја тела (уодносу на друга тела) три
ФИЗИКА 1. Понедељак, 8. октобар, 1. Кинематика тачке у једној димензији Кинематикакретањаудведимензије 1 Кинематика кретање свејеустањукретања кретање промена положаја тела (уодносу на друга тела) три
UNIVERZITET U ZENICI
 8 GRUPA A UNIVERZITET U ZENICI MAŠINSKI FAKULTET PISMENI ISPIT IZ MATEMATIKE Riješiti matriču jedačiu: ( A+ B) AX = A, gdje matrice A i B zadovoljavaju: A =, B = y + z Naći tačku simetriču tački M(,-,)
8 GRUPA A UNIVERZITET U ZENICI MAŠINSKI FAKULTET PISMENI ISPIT IZ MATEMATIKE Riješiti matriču jedačiu: ( A+ B) AX = A, gdje matrice A i B zadovoljavaju: A =, B = y + z Naći tačku simetriču tački M(,-,)
Konstr
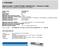 7. FTG10OM1 BEZHALOGENI VATROOTPORNI ENERGETSKI I SIGNALNI KABEL Izolirani gumom G10 i oplašteni termoplastičnim LSOH plaštem Tipska oznaka: FTG10OM1 E90 Norma: CEI 20-45 Nazivni napon: 0, 6 / 1 kv Ispitni
7. FTG10OM1 BEZHALOGENI VATROOTPORNI ENERGETSKI I SIGNALNI KABEL Izolirani gumom G10 i oplašteni termoplastičnim LSOH plaštem Tipska oznaka: FTG10OM1 E90 Norma: CEI 20-45 Nazivni napon: 0, 6 / 1 kv Ispitni
RG_V_05_Transformacije 3D
 Računarska grafika - vežbe 5 Transformacije u 3D grafici Transformacije u 3D grafici Slično kao i u D grafici, uz razlike: matrice su 4x4 postoji posebna matrica projekcije Konvencije: desni pravougli
Računarska grafika - vežbe 5 Transformacije u 3D grafici Transformacije u 3D grafici Slično kao i u D grafici, uz razlike: matrice su 4x4 postoji posebna matrica projekcije Konvencije: desni pravougli
КОНАЧНИ ЗАХТЕВ ЗА ПРИКЉУЧЕЊЕ ЕЛЕКТРОЕНЕРГЕТСКОГ ОБЈЕКТА НА ПРЕНОСНУ МРЕЖУ
 ЗАХТЕВ ЗА ПРИКЉУЧЕЊЕ НА ПРЕНОСНИ СИСТЕМ објекта а електричне енергије Напомена: У случају повлачења, односно одустанка од поднетог захтева, подносилац захтева је дужан да сноси све трошкове који су настали
ЗАХТЕВ ЗА ПРИКЉУЧЕЊЕ НА ПРЕНОСНИ СИСТЕМ објекта а електричне енергије Напомена: У случају повлачења, односно одустанка од поднетог захтева, подносилац захтева је дужан да сноси све трошкове који су настали
Primjena neodredenog integrala u inženjerstvu Matematika 2 Erna Begović Kovač, Literatura: I. Gusić, Lekcije iz Matematike 2
 Primjena neodredenog integrala u inženjerstvu Matematika 2 Erna Begović Kovač, 2019. Literatura: I. Gusić, Lekcije iz Matematike 2 http://matematika.fkit.hr Uvod Ako su dvije veličine x i y povezane relacijom
Primjena neodredenog integrala u inženjerstvu Matematika 2 Erna Begović Kovač, 2019. Literatura: I. Gusić, Lekcije iz Matematike 2 http://matematika.fkit.hr Uvod Ako su dvije veličine x i y povezane relacijom
1
 PROVOđENJE TOPLOTE ovođenje toplote ili kondukcija je način kretanja toplote koji je svojstven čvrsti aterijalia, iako se pojavljuje (ali sa anearljivi inteniteto) i kod luida. Karakteristika aterijala
PROVOđENJE TOPLOTE ovođenje toplote ili kondukcija je način kretanja toplote koji je svojstven čvrsti aterijalia, iako se pojavljuje (ali sa anearljivi inteniteto) i kod luida. Karakteristika aterijala
Microsoft PowerPoint - HG_1_2012
 JEŽBE 1 -STRUKTURA ODONOSNIKA - TEČENJE U PODZEMLJU Split, 28. ožujka 2012. Struktura odonosnika TRODIJELNA STRUKTURA TLA: POJAM POROZNOSTI: Totalna poroznost n oluen pora oluen uzorka 100 100 Efektina
JEŽBE 1 -STRUKTURA ODONOSNIKA - TEČENJE U PODZEMLJU Split, 28. ožujka 2012. Struktura odonosnika TRODIJELNA STRUKTURA TLA: POJAM POROZNOSTI: Totalna poroznost n oluen pora oluen uzorka 100 100 Efektina
Microsoft Word - 4.Ucenik razlikuje direktno i obrnuto proporcionalne velicine, zna linearnu funkciju i graficki interpretira n
 4. UČENIK RAZLIKUJE DIREKTNO I OBRNUTO PROPORCIONALNE VELIČINE, ZNA LINEARNU FUNKCIJU I GRAFIČKI INTERPRETIRA NJENA SVOJSTVA U fajlu 4. iz srednjeg nivoa smo se upoznali sa postupkom rada kada je u pitanju
4. UČENIK RAZLIKUJE DIREKTNO I OBRNUTO PROPORCIONALNE VELIČINE, ZNA LINEARNU FUNKCIJU I GRAFIČKI INTERPRETIRA NJENA SVOJSTVA U fajlu 4. iz srednjeg nivoa smo se upoznali sa postupkom rada kada je u pitanju
Tehnicko crtanje 2010-pitanja
 ПИТАЊА ИЗ ТЕХНИЧКОГ ЦРТАЊА 1. Нацртати трећу прејекцију 2 2. Нацртати трећу прејекцију 2 3. Нацртати трећу прејекцију 2 4. Нацртати сва три изгледа модела приказаног у изометрији 2 5. Нацртати сва три
ПИТАЊА ИЗ ТЕХНИЧКОГ ЦРТАЊА 1. Нацртати трећу прејекцију 2 2. Нацртати трећу прејекцију 2 3. Нацртати трећу прејекцију 2 4. Нацртати сва три изгледа модела приказаног у изометрији 2 5. Нацртати сва три
EMC doc
 ИСПИТ ИЗ ЕЛЕКТРОМАГНЕТСКЕ КОМПАТИБИЛНОСТИ 28. мај 2018. Напомена. Испит траје 120 минута. Дозвољена је употреба литературе и рачунара. Коначне одговоре уписати у одговарајуће кућице, уцртати у дате дијаграме
ИСПИТ ИЗ ЕЛЕКТРОМАГНЕТСКЕ КОМПАТИБИЛНОСТИ 28. мај 2018. Напомена. Испит траје 120 минута. Дозвољена је употреба литературе и рачунара. Коначне одговоре уписати у одговарајуће кућице, уцртати у дате дијаграме
Зборник радова 6. Међународне конференције о настави физике у средњим школама, Алексинац, март Нелинеарно еластично клатно Милан С. Коваче
 Нелинеарно еластично клатно Милан С. Ковачевић 1, Мирослав Јовановић 2 1 Природно-математички факултет, Крагујевац, Србија 2 Гимназија Јосиф Панчић Бајина Башта, Србија Апстракт. У овом раду је описан
Нелинеарно еластично клатно Милан С. Ковачевић 1, Мирослав Јовановић 2 1 Природно-математички факултет, Крагујевац, Србија 2 Гимназија Јосиф Панчић Бајина Башта, Србија Апстракт. У овом раду је описан
Microsoft PowerPoint - STABILNOST KONSTRUKCIJA 4_19 [Compatibility Mode]
![Microsoft PowerPoint - STABILNOST KONSTRUKCIJA 4_19 [Compatibility Mode] Microsoft PowerPoint - STABILNOST KONSTRUKCIJA 4_19 [Compatibility Mode]](/thumbs/99/141489570.jpg) Univerzitet u Beogradu Građevinski fakutet Katedra za tehničku mehaniku i teoriju konstrukcija STABILNOST KONSTRUKCIJA IV ČAS V. PROF. DR MARIJA NEFOVSKA DANILOVIĆ 3. SABILNOST KONSTRUKCIJA 1 Geometrijska
Univerzitet u Beogradu Građevinski fakutet Katedra za tehničku mehaniku i teoriju konstrukcija STABILNOST KONSTRUKCIJA IV ČAS V. PROF. DR MARIJA NEFOVSKA DANILOVIĆ 3. SABILNOST KONSTRUKCIJA 1 Geometrijska
My_P_Trigo_Zbir_Free
 Штa треба знати пре почетка решавања задатака? ТРИГОНОМЕТРИЈА Ниво - Основне формуле које произилазе из дефиниција тригонометријских функција Тригонометријске функције се дефинишу у правоуглом троуглу
Штa треба знати пре почетка решавања задатака? ТРИГОНОМЕТРИЈА Ниво - Основне формуле које произилазе из дефиниција тригонометријских функција Тригонометријске функције се дефинишу у правоуглом троуглу
Microsoft Word - DEPCONV.SERBO_CIR.doc
 1 СВИ ПОДАЦИ О КАБИНИ ЗА ЛАКОВАЊЕ КРАТКЕ УПУТЕ ЗА ИЗРАЧУН И ОДАБИР ФИЛТЕРА ЗА ЧЕСТИЦЕ БОЈЕ Економично и еколошки исправно управљање кабинама за лаковање распршивањем постиже се провером неких основних
1 СВИ ПОДАЦИ О КАБИНИ ЗА ЛАКОВАЊЕ КРАТКЕ УПУТЕ ЗА ИЗРАЧУН И ОДАБИР ФИЛТЕРА ЗА ЧЕСТИЦЕ БОЈЕ Економично и еколошки исправно управљање кабинама за лаковање распршивањем постиже се провером неких основних
Projektovanje analognih integrisanih kola Projektovanje analognih integrisanih kola Prof. Dr Predrag Petković, Dejan Mirković Katedra za elektroniku E
 Projektovanje analognih integrisanih kola Projektovanje analognih integrisanih kola Prof Dr Prerag Petković, Dejan Mirković Katera za elektroniku Elektronski fakultet Niš Saržaj: Uvo Lejaut analognih oula
Projektovanje analognih integrisanih kola Projektovanje analognih integrisanih kola Prof Dr Prerag Petković, Dejan Mirković Katera za elektroniku Elektronski fakultet Niš Saržaj: Uvo Lejaut analognih oula
Toplinska i električna vodljivost metala
 Električna vodljivost metala Cilj vježbe Određivanje koeficijenta električne vodljivosti bakra i aluminija U-I metodom. Teorijski dio Eksperimentalno je utvrđeno da otpor ne-ohmskog vodiča raste s porastom
Električna vodljivost metala Cilj vježbe Određivanje koeficijenta električne vodljivosti bakra i aluminija U-I metodom. Teorijski dio Eksperimentalno je utvrđeno da otpor ne-ohmskog vodiča raste s porastom
1 MATEMATIKA 1 (prva zadaća) Vektori i primjene 1. U trokutu ABC točke M i N dijele stranicu AB na tri jednaka dijela. O
 http://www.fsb.hr/matematika/ (prva zadać Vektori i primjene. U trokutu ABC točke M i N dijele stranicu AB na tri jednaka dijela. Označite CA= a, CB= b i izrazite vektore CM i CN pomoću vektora a i b..
http://www.fsb.hr/matematika/ (prva zadać Vektori i primjene. U trokutu ABC točke M i N dijele stranicu AB na tri jednaka dijela. Označite CA= a, CB= b i izrazite vektore CM i CN pomoću vektora a i b..
vjezbe-difrfv.dvi
 Zadatak 5.1. Neka je L: R n R m linearni operator. Dokažite da je DL(X) = L, X R n. Preslikavanje L je linearno i za ostatak r(h) = L(X + H) L(X) L(H) = 0 vrijedi r(h) lim = 0. (5.1) H 0 Kako je R n je
Zadatak 5.1. Neka je L: R n R m linearni operator. Dokažite da je DL(X) = L, X R n. Preslikavanje L je linearno i za ostatak r(h) = L(X + H) L(X) L(H) = 0 vrijedi r(h) lim = 0. (5.1) H 0 Kako je R n je
Univerzitet u Beogradu
 Univerzitet u Beogradu Elektrotehnički fakultet Odsek za energetiku Smer: Elektroenergetski sistemi Računarske vežbe: PROJEKTOVANJE POMOĆU RAČUNARA U ELEKTROENERGETICI -zaštita od udara groma- Dr Zlatan
Univerzitet u Beogradu Elektrotehnički fakultet Odsek za energetiku Smer: Elektroenergetski sistemi Računarske vežbe: PROJEKTOVANJE POMOĆU RAČUNARA U ELEKTROENERGETICI -zaštita od udara groma- Dr Zlatan
U N I V E R Z I T E T U Z E N I C I U N I V E R S I TA S S T U D I O R U M I C A E N S I S Z E N Univerzitet u Zenici Mašinski fakultet Aleksandar Kar
 U N I V E R Z I T E T U Z E N I C I U N I V E R S I T S S T U D I O R U M I C E N S I S Z E N Univerzitet u Zenici Mašinski fakultet leksandar Karač Riješeni ispitni zadaci iz Otpornosti materijala Zenica,
U N I V E R Z I T E T U Z E N I C I U N I V E R S I T S S T U D I O R U M I C E N S I S Z E N Univerzitet u Zenici Mašinski fakultet leksandar Karač Riješeni ispitni zadaci iz Otpornosti materijala Zenica,
Ефекти реолошких карактеристика бетона
 Смицање у спрегнутим бетонским пресецима 1 Смицање у споју спрегнутих пресека 2 Смицање у споју композитног бетонског пресека 3 Смицање и попречно савијање 4 Интеракција торзије и трансверзалних сила 5
Смицање у спрегнутим бетонским пресецима 1 Смицање у споју спрегнутих пресека 2 Смицање у споју композитног бетонског пресека 3 Смицање и попречно савијање 4 Интеракција торзије и трансверзалних сила 5
?? ????????? ?????????? ?????? ?? ????????? ??????? ???????? ?? ??????? ??????:
 РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 003 АСИНХРОНЕ МАШИНЕ Трофазни асинхрони мотор са намотаним ротором има податке: 380V 10A cos ϕ 08 Y 50Hz p отпор статора R s Ω Мотор је испитан
РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 003 АСИНХРОНЕ МАШИНЕ Трофазни асинхрони мотор са намотаним ротором има податке: 380V 10A cos ϕ 08 Y 50Hz p отпор статора R s Ω Мотор је испитан
1. GRUPA Pismeni ispit iz MATEMATIKE Prezime i ime broj indeksa 1. (15 poena) Rexiti matriqnu jednaqinu 3XB T + XA = B, pri qemu
 1. GRUPA Pismeni ispit iz MATEMATIKE 1 0.0.01. Prezime i ime broj indeksa 1. (15 poena) Rexiti matriqnu jednaqinu XB T + XA = B, 1 4 pri qemu je A = 6 9 i B = 1 1 0 1 1. 4 4 4 8 1. Data je prava q : {
1. GRUPA Pismeni ispit iz MATEMATIKE 1 0.0.01. Prezime i ime broj indeksa 1. (15 poena) Rexiti matriqnu jednaqinu XB T + XA = B, 1 4 pri qemu je A = 6 9 i B = 1 1 0 1 1. 4 4 4 8 1. Data je prava q : {
Analiticka geometrija
 Analitička geometrija Predavanje 8 Vektori u prostoru. Skalarni proizvod vektora Novi Sad, 2018. Milica Žigić (PMF, UNS 2018) Analitička geometrija predavanje 8 1 / 11 Vektori u prostoru i pravougli koordinatni
Analitička geometrija Predavanje 8 Vektori u prostoru. Skalarni proizvod vektora Novi Sad, 2018. Milica Žigić (PMF, UNS 2018) Analitička geometrija predavanje 8 1 / 11 Vektori u prostoru i pravougli koordinatni
Microsoft PowerPoint - Teorija kretanja vozila-predavanje 4.1.ppt
 ТЕОРИЈА КРЕТАЊА ВОЗИЛА Предавање 4.1 гусенична возила, отпори кретања, Код дефинисања параметара функција кретања возила на гусеницама разматрају се следећи случајеви кретања: а) праволиниjско кретање
ТЕОРИЈА КРЕТАЊА ВОЗИЛА Предавање 4.1 гусенична возила, отпори кретања, Код дефинисања параметара функција кретања возила на гусеницама разматрају се следећи случајеви кретања: а) праволиниjско кретање
Slide 1
 BETONSKE KONSTRUKCIJE 2 vježbe, 12.-13.12.2017. 12.-13.12.2017. DATUM SATI TEMATSKA CJELINA 10.- 11.10.2017. 2 17.-18.10.2017. 2 24.-25.10.2017. 2 31.10.- 1.11.2017. uvod ponavljanje poznatih postupaka
BETONSKE KONSTRUKCIJE 2 vježbe, 12.-13.12.2017. 12.-13.12.2017. DATUM SATI TEMATSKA CJELINA 10.- 11.10.2017. 2 17.-18.10.2017. 2 24.-25.10.2017. 2 31.10.- 1.11.2017. uvod ponavljanje poznatih postupaka
SADRŽAJ GLAVNOG PROJEKTA
 Izradio: Građevina: Mapa: Vrsta projekta (razina i struka): Zajednička oznaka projekta: INSTITUT IGH d.d. 10 000 Zagreb, Janka Rakuše 1 JUŽNA OBILAZNICA GRADA OSIJEKA, DOGRADNJA JUŽNOG KOLNIKA, DIONICA:
Izradio: Građevina: Mapa: Vrsta projekta (razina i struka): Zajednička oznaka projekta: INSTITUT IGH d.d. 10 000 Zagreb, Janka Rakuše 1 JUŽNA OBILAZNICA GRADA OSIJEKA, DOGRADNJA JUŽNOG KOLNIKA, DIONICA:
Jednadžbe - ponavljanje
 PRIMJENE NA PRAVOKUTNI TROKUT sin = sin β = cos = cos β = tg kuta tg = tg β = ctg kuta ctg = ctg β = c = p + q Ako su kutovi u trokutu 30 i 60 onda je hipotenuza dva puta veća od kraće katete (c = 2a ili
PRIMJENE NA PRAVOKUTNI TROKUT sin = sin β = cos = cos β = tg kuta tg = tg β = ctg kuta ctg = ctg β = c = p + q Ako su kutovi u trokutu 30 i 60 onda je hipotenuza dva puta veća od kraće katete (c = 2a ili
