Univerzitet u Ni²u PRIRODNO-MATEMATIƒKI FAKULTET Departman za informatiku Ugraživanje re i i fraza u vektorske prostore i polu-nadgledano otkrivanje s
|
|
|
- Marija Marjanović
- пре 6 година
- Прикази:
Транскрипт
1 Univerzitet u Ni²u PRIRODNO-MATEMATIƒKI FAKULTET Departman za informatiku Ugraživanje re i i fraza u vektorske prostore i polu-nadgledano otkrivanje semanti kih sli nosti Master rad Kandidat: Jelena Milovanovi Br. indeksa: 2 Ni², septembar Mentor: Prof. dr Branimir Todorovi
2
3 Veliku zahvalnost dugujem svim profesorima Prirodno-matemati kog fakulteta koji su moje oskudno znanje iz oblasti informatike strpljivo i sistemati no unapreživali i od mene stvorili ambicioznog i perspektivnog programera. Zahvaljujem se porodici, koja me podrºava u svemu ²to volim i mentoru koji me u i da volim prave stvari.
4
5 Sadrºaj 1 Uvod N ili jedan-od kodiranje (eng. One-hot) Modeli za ugraživanje re i u vektorske prostore(eng. Word embeddings) Distributivna hipoteza Ugradnja re i i fraza u vektorski prostor Detekcija fraza Modeli jezika bazirani na neuronskim mreºama sa jednosmernim prostiranjem signala(feed forward neural network language model-ffnnlm) Word2Vec modeli Model kontinualne grupe re i (eng.continuous bag of words -CBOW ) Kontekst duºine jedan Model Treniranje Kontekst od vi²e re i Model preskakanja jedinica (eng Skip-gram) Model Treniranje Optimizacija Hijerarhijski sloj izlaznih neurona(eng. Hierarchical softmax) Model Treniranje Konstrukcija hijerarhijskog stabla Uzimanje negativnih uzoraka (eng.negative sampling) Model Treniranje
6 SADRšAJ Performanse Vi²enitno treniranje Dimenzionalnost vektora Izbor arhitekture Veli ina prozora Eliminisanje re i sa velikom ili malom u estano² u Unapreženje Promenljiva veli ina prozora Nelinearni konteksti Klasterovanje Hibridni algoritam Ekasnost i efektivnost Klasterizacija metodom k-srednjih vrednosti (eng K- means) Ubrzanje Aglomerativno hijerarhijsko klasterovanje Lanac najbliºih suseda Sloºenost Obrada podataka Se enje stabla Vizuelizacija i rezultati Efektivnost Ekasnost Zaklju ak 44 Literatura 45 Biograja 47
7 Glava 1 Uvod U ovom radu predlaºe se i opisuje metod za polu-nadgledano dobijanje informacija bazirano na distributivnoj vektorskoj reprezentaciji re i i fraza, koriste i Word2Vec modele za dobijanje vektora i hijerarhijsko aglomerativno klasterovanje za izdvajanje informacija. Word2Vec [2] je skra enica kojom su predstavljeni modeli koji se koriste za ugraživanje re i u vi²edimenzione vektorske prostore. Ugraživanje se zasniva na Distributivnoj hipotezi da re i i fraze koje su se javljale u istim kontekstima imaju sli no zna enje. Ovakav pristup informacije bitne za zna enje re i ne crpi iz same re i vec iz konteksta. U dobijenom vektorskom prostoru, sintaksne i semanti ke relacije predstavljene su relativnim poloºajima vektora. Karakteristike dobijenog prostora su prou avane u radu [1]. Prvi korak vektorske ugradnje re i i fraza je detektovanje fraza koris enjem uzajamne informacije ta aka(eng, Pointwise Mutual Information) kao meru povezanosti. Zatim WordToVec model treniramo na korpusu sastavljenom od prijava za posao. Dobijeni vektorski prostor predstavljamo dendrogramom dobijenim odozdo-na gore(eng. bottom-up) hierarhijskim klasterovanjem. Uzimaju i poznate re i kao semena i se enjem stabla u voru koji je najbliºi zajedni ki predak ovih re i dobijaju se klasteri koji pored ovih re i sadrºe i re i koje su semanti ki vrlo sli ne njima. Time omogu avamo izdvajajne manje poznatih termina semanti ki sli nih semenima. U radu predstavljam na in nalaºenja pojmova koji se javljaju u korpusu a korisniku nisu poznati. U re²avanju problema WordToVec model i hierarhijsko klasterovanje igraju glavnu ulogu pa e biti detaljno obja²njeni. 4
8 GLAVA 1. UVOD N ili jedan-od kodiranje (eng. One-hot) Posmatrajmo proste vektorske modele, gde je dimenzija vektora jednaka duºini re nika. Svaka r c predstavljena je retkim vektorom koji ima jedinicu na jednom mestu i ostale nule. Slika 1.1: One-hot kodiranje re i Ovakva reprezentacija, osim ²to je memorijski zahtevna o igledno ne sadrºi nikakvu informaciju o re ima i njihovom mežusobnom odnosu. Za smanjenje dimenzionalnosti moºe se koristiti dekompozicija po sopstvenim vrednostima(eng. Singular value decomposition). Slika 1.2: X-matrica vektora re i. U-ortogaonalna matrica koja sadrºi sopstvene vektore matrice XX T D-je dijagonalna matrica koja sadrºi sopstvene vrednosti matrice XX T X T X ili Za matricu dimenzija d n sloºenost SVD je O(nd 2 ). Ovakva redukcija je nemogu a za veliki broj re i u dokumentu. Zato je najbolje direktno izra unavati vektore male dimenzionalnosti. 1.2 Modeli za ugraživanje re i u vektorske prostore(eng. Word embeddings) Sistemi za procesiranje jezika su re i tretirali kao atomske simbole tako da su npr. re i ovek i ºena predstavljeni potpuno proizvoljnim simbolima
9 GLAVA 1. UVOD 6 (npr. ºena id124 i ovek id392) koji nisu imali veze jedan sa drugim. Ovakav pristup ne pruºa korisne informacije o odnosu izmežu dve re i. Modeli za ugraživanje re i u vektorske prostore(eng. Word embeddings) projektuju (ugražuju) re i i fraze u vektorski prostor realnih brojeva tako da su re i semant icki sli nog zna enja u blizini. Metodi za mapiranje re i i fraza uklju- uju neuronske mreºe, redukciju dimenzija matrice uzajamnog pojavljivanja re i(eng. co-ocurence matrix), probabilisti ke modele... Svi metodi se, manje ili vi²e, baziraju na Distributivnoj hipotezi. Kod ovakvih modela token sam po sebi ne nosi nikakvu informaciju ve je njegov vektor uslovljen kontekstom u kom se nalazi. 1.3 Distributivna hipoteza Re i karakteri²e okruºenje u kojem se nalaze Dºon Rupert Fert U lingvistici distributivna hipoteza pripada oblast semantike i tvrdi da re i koje se nalaze u istom kontekstu teºe da imaju isto semanti ko zna enje. Ona je osnova semanti ke statistike, oblasti koja se bavi upotrebom statisti kih pravilnosti za razumevanje jezika. Njena na ela ²iroko se koriste u oblasti kognitivnih nauka pa i u oblasti ve²ta ke inteligencije. Postoje razli iti pristupi kori± enju ove hipoteze i moºemo ih svrstati u dva osnovna: metodi zasnovani na brojanju i metodi zasnovani na predvižanju. Metodi zasnovani na brojanju koriste statistiku pojavljivanja re i u okolini drugih re i u korpusu i tu informaciju koriste za stvaranje vektora, dok prediktivni metodi predvižaju re u zavisnosti od konteksta u kome se nalazi i vektore uzimaju kao parametre modela. Ovi metodi detaljnije su obraženi u radu [3].
10 Glava 2 Ugradnja re i i fraza u vektorski prostor 2.1 Detekcija fraza Za detekciju fraza koristi emo uzajamno pojavljivanje ta aka(eng. Pointvise Mutual Information) kao meru povezanosti re i. PMI je jedinica povezanosti dva dogažaja i dobija se: pmi(x; y) = log p(x, y) p(x)p(y) (2.1) Gde su x i y vrednosti diskretnih slu ajnih promenljivih X i Y,p(x, y) verovatno a zajedni kog a p(x),p(y) pojedina nih dogažaja. Ideja se zasniva na tome da na osnovu odnosa zajedni kog i pojedina og pojavljivanja dve re i dožemo do zaklju ka da su se re i javljale jedna do druge u tekstu zna ajno vi²e puta nego ²to o ekujemo na osnovu njihovog pojedina nog pojavljvanja. U algoritmu koristimo formulu score(w1, w2) = count(w1, w2) δ count(w1)count(w2) (2.2) Gde je count(x) broj pojavljivanja re i u tekstu. Parametar δ je uveden da bi se spre ilo formiranje velikog broja fraza od re i koje su se malo puta javile u tekstu. Fraze se detektuju pre treniranja i duºina je uslovljena brojem iteracija. U prvoj iteraciji pravimo bigrame, a zatim ponavljanjem postupka i smanjivanjem praga za izbor fraza, pravimo fraze koje se sastoje od ve eg broja re i. Pravljenje fraza obja²njeno je u radu [4] 7
11 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR Modeli jezika bazirani na neuronskim mre- ºama sa jednosmernim prostiranjem signala(feed forward neural network language model-ffnnlm) Za distribuiranu reprezenetaciju re i koriste se mnogi modeli. Pokazalo se da modeli neuronskih mreºa daju zna ajnije bolje rezultate u pogledu linearnih regularnosti izmežu re i. FFNNLM je n-gram model koji odrežuje raspodelu re i na osnovi n-1 re i koje su se javile pre nje koriste i neuronsku mreºu. Mreºa se sastoji ulaznog, projekscionog, skrivenog i izlaznog sloja. Slika 2.1: FFNNLM Kao ulaz u neuronsku mreºu imamo n-1 prethodnih re i predstavljenih retkim vektorom, dimenzije re nika (V) sa jedinicom na samo jednoj poziciji (one-hot kodiranje) koja zapravo, ozna ava indeks re i. Svaka ulazna re se projektuje na vektor realnih brojeva matricom VxP. Sloj dobijen nadovezivanjem ovih vektora je projekcioni sloj. Broj neurona u ovom sloju iznosi (n 1) P (n-1 broj re i na ulazu, P je duºina vektora (tj. broj karakteristika eng.feature) koje se koriste za reprezentaciju svake re i). Ista matrica teºina se koristi za projekcuju svake re i. Ako je M matrica koja predstavlja
12 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 9 teºinu sinapsi izmežu projekcionog i skrivenog sloja, c linearna aktivaciona funkcija projekcionog sloja, b pomeraj, tada je aktivaciona funkcija j-tog neurona skrivenog sloja: (n 1)P d j = tanh( i=1 c i M ji + b j ) (2.3) Broj neurona u izlaznom sloju odgovara veli ini re nika. Aktivaciona funkcija izlaznog sloja je softmax funkcija i predstavlja verovatno u pojavljivanja re i za dat ulaz (p(w i w i 1, w i 2,..., w i n+1 )) Neka je V matrica teºina izmežu skrivenog i izlaznog sloja, b pomeraj i H broj neurona u skrivenom sloju, tada je izlaz iz j-tog izlaznog neurona o j = H V ji d i + b j (2.4) i=1 p j = e o i V i=1 eo i (2.5) Ovakvi modeli imaju veliku kompleksnost izra unavanja(zbor nelineranog skrivenog sloja) ²to ih ini neprakti nim za velike koli ine podataka. Zato su istraºivanja krenula u pravcu modela koji daju manje precizne podatke ali mogu da treniraju na mnogo ve em korpusu sa ve om ekasno² u. Vi²e o ovome moºe se na i u radovima [5], [6] i [7] 2.3 Word2Vec modeli Word2Vec ine dva modela: kontinualna grupa re i (eng. Continuous bag of words) i preskakanje jedinica( eng. Skip- gram) koji se mogu trenirati metodom hijerarhijskog izlaznog sloja(eng.hierarchical softmax ) ili metodom negativnih uzoraka (eng.negative sampling) Ovo su prediktivni distributivni modeli koji su privukli veliku paºnju u oblasti Obrade prirodnih jezika(oblasti lingvistike i ve²ta ke iteligencije koja se bavi interakcijom prirodnih jezika i jezika koje koriste ra unari). Vektori re i dobijeni ovim modelima na apstraktnom nivou zapravo reprezentuju zna enje re i. Dimenzije vektora same po sebi ne nose nikakvu informaciju, ono ²to nam pruºa uvid u semanti ke i sintaksi ke osobine re i i lingvisti ke odnose mežu njima je mežusobni poloºaj vektora u prostoru dobijenim treniranjem Word2vec modela. Word2Vec daje vektore dimenzija nekoliko stotina (najbolji rezultati sa dimenzijamo oko 500) gde je re predstavljena rasporedom teºina po ovim
13 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 10 dimenzijama. Dakle, umesto 1-1 mapiranja izmežu elementa vektora i re i, reprezentacija re i je rasporežena duº svih koordinata i svaka koordinata doprinosi zna enju r ci. Treniranjem na velikim korpusima mogu e je dobiti vektore koji izuzetno ekasno reprezentuju odnose izmežu re i. Neke relacije dobijaju se prostim oduzimanjem vektora npr v(macke) v(macka) = v(ljudi) v(covek). Na slici su prikazane neke od sintaksi kih regularnosti. Slika 2.2: Dvodimenziona projekcija 1000-dimenzionih Skip-gram vektora dobijena metodom glavnih komponenti (eng Principal component analysis ) Mežutim vektori sadrºe i mnogo sloºenije informacije osim prostih sintaksi kih relacija. Ovako dobijen prostor daje odgovore i na pitanja poput king : man =? : woman Slika 2.3: Kompozicijom vektora otkrivaju se semanti ke relacije izmežu re i
14 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 11 Rezultati dobijeni prostim operacijama oduzimanja i sabiranja nad vektorima pokazuju izvanredne karakteristike ovog prostora. Testovi pokazuju uspe²no analogijsko povezivanje i na semanti kim zadacima sa frazama. Slika 2.4 Na primeru relacije izmežu gradova i drºava na slici 2.6 uo avamo da iako prilikom treniranja nismo dali nikakvu dodatnu informaciju o gradu ili drºavi, model je sposoban da samo na osnovu konteksta re i automatski organizuje koncepte i nau i vezu mežu njima. Slika 2.5: Dvodimenziona projekcija 1000-dimenzionih Skip-gram vektora dobijena metodom glavnih komponenti (eng Principal component analysis ) Za merenje kvaliteta dobijenih vektora koristi se i ta nost u re²avanju
15 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 12 semanti ki zahtevnih zadataka. U [2] koriste test skup koji se sastoji iz 5 tipova semanti kih i 9 tipova sintaksi kih pitanja. Na slici je dat primer analogija koje se koriste za testiranje. Slika 2.6: Primer semanti kih i sintaksi kih regularnosti koje ocenjuju kvalitet vektora Model kontinualne grupe re i (eng.continuous bag of words -CBOW ) CBOW arhitekruta predviža re u zavisnosti od konteksta. Duºinom prozora odrežuje se kontekst koji se posmatra i koji uklju uje re i koje su se javile pre i posle trenutne re i. Ovaj model dobio je ime grupa re i (eng. bag-of -words) jer redosled re i na ulazu ne uti e na ishod. Kod kontinualne grupe re i, re i su predstavljene kontinualnim gustim vektorima malih dimenzija za razliku od ne-kontilnualne, gde su re i predstavljene Onehot vektorima.
16 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 13 Slika 2.7: CBOW model Sli na je FFNNLM s tim ²to ne postoji skriveni sloj i projekcioni sloj je zajedni ki za sve re i. Nema nadovezivanja karakteristika, projekcija svih vektora je ista i predstavlja aritmeti ku sredinu vektora dobijenih mnoºenjem 1-N reprezentacija re i istom matricom W=VxP. Slika 2.8: CBOW model
17 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR Kontekst duºine jedan Model Za po etak, radi jednostavnosti, kao ulaz posmatramo kontekst duºine jedan, odnosno samo re koja se javila pre trenutne re i. Na slici je prikazana neuronska mreºa. Slika 2.9: CBOW model x k h i prestavlja sinapsu izmežu k-tog ulaznog neurona i i-tog skrivenog Ulaz u neuronsku mreºu je re kodirana 1-N vektorom sa jedinicom na mestu indeksa te re i u re niku, a izlaz su verovatno e pojavljivanja svake od re i u njenom kontekstu. Neuroni skrivenog sloja imaju lineranu aktivacionu funkciju dakle, izlaz je jednak potencijalu. Izlazni sloj je sloj softmax neurona. Sa w i predstavljam re na i-tom mestu u re niku. Veli ina ulaznog sloja jednaka je duºini re nika-v. Izlaz iz ulaznog sloja ozna ava u sa x. Veli ina skrivenog sloja je proizvoljna i ozna i u je sa p, a izlaz iz tog sloja ozna- i u vektorom h. Veli ina izlaznog sloja jednaka je duºini re nika i izlaz u ozna iti vektorom y. Potencijal izlaznog sloja ozna avam sa u. Svi slojevi su mežusobom potpuno povezani. Teºine sinapsi izmežu ulaznog i skrivenog sloja predstavi u matricom W = w ij.
18 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 15 weight(x 1 h 1 ) weight(x 1 h 2 )... weight(x 1 h p ) weight(x 2 h 1 ) weight(x 2 h 2 )... weight(x 2 h p ) W vxp = weight(x v h 1 ) weight(x v h 2 )... weight(x v h p ) (2.6) Gde je elija w ij jednaka teºini sinapse izmežu i-tog neurona ulaznog sloja i j-tog neurona skrivenog sloja. Tu vezu ozna i u sa x i h j. Prime ujemo da kolona i predstavlja teºine sinapsi izmežu i-tog neurona skrivenog sloja i neurona ulaznog sloja. Vrsta j predstavlja teºine sinapsi izmežu j-tog neurona ulaznog sloja i neurona skrivenog sloja. Ovaj vektor zovemo ulazni vektor re i w j i ozna avamo ga sa vj u. Vrste matrice su zapravo p-dimenziona reprezentacija re i. h j = v x i w ij (2.7) i=1 S obzirom da je x retki vektor sa jedinicom na mestu indeksa ulazne re i: h = x T W = W k: = v u k (2.8) Slika 2.10: Teºine sinapsi izmežu ulaznog i skrivenog sloja Teºine sinapsi izmežu skrivenog i izlaznog sloja predstavi u matricom W = w ij. k-ta kolona matrice predstavlja vektor teºina sinapsi izmežu i k-tog neurona izlaznog sloja i neurona skrivenog sloja, ozna ava u ga sa v k i zovemo ga izlazni vektor re i w k
19 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 16 weight(h 1 u 1 ) weight(h 1 u 2 )... weight(h 1 u v ) weight(h 2 u 1 ) weight(h 2 u 2 )... weight(h 2 u v ) W pxv = weight(h p u 1 ) weight(h p u 2 )... weight(h p u v ) (2.9) Izlaz iz j-tog izlaznog neurona predstavlja uslovnu verovatno u pojavljivanja re i w j u kontekstu ulazne re i w ulazna. u j = p h i w ij -potencijal j-tog izlaznog neurona (2.10) i=1 p(w j w ulazna ) = y j = Treniranje exp u j v i=1 exp u -izlaz j-tog izlaznog neurona (2.11) i p(w j w ulazna ) = y j = h = v u ulazna (2.12) W :j = v i j (2.13) u j = v ut ulaznav i j (2.14) exp vulazna ut vi j v k=1 exp vit k vu ulazna (2.15) Kriterijumska funkcija koju prilikom treniranja minimiziramo je negativni logaritam verodostojnosti. Dakle cilj treniranja je min( log(p(w p w u ; W, W )) gde je p(prava) indeks re i koja bi po trening primeru trebalo da bude u kontekstu ulazne, iji je indeks u. E = log(p(w p w u )) = (2.16) = log exp u p v i=1 exp u i = (2.17) = log exp u p + log = u p + log v exp u i = (2.18) i=1 v exp u i (2.19) i=1
20 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 17 Primer: Cats drink milk. Ako je drink ulazna re, kriterijumska funkcija je log(p(milk drink; W, W )). Za nalaºenje minimuma koristimo stohasti ki gradijentni spust.aºuriranje teºina predstavljeno je slede om jedna inom w (new) ij w new ij = w (old) ij = w old ij η w ij (2.20) η w ij (2.21) Pri emu je η > 0 korak u enja. Za nalaºenje gradijenta koristimo tehniku propagiranja gre²ke u nazad (eng.back propagation). Aºuriranje izlaznih vektora re i w ij = u j uj w ij (2.22) u j w ij = h i (2.23) = ( u p + log v i=1 exp u i) = (2.24) u j uj 1 = t j + v i=1 exp u exp u j = (2.25) i = y j t j = e j (2.26) { 1 j = p t j = (2.27) 0 j p t j je jednak jedinici samo ako je w j konteksna re iz trening primera.u drugom slu aju je 0. e j zapravo predstavlja funkciju gubitka w (new) ij e j = y j t j (2.28) w ij = e jh i (2.29) = w (old) ij ηe j h i (2.30)
21 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 18 v i(new) j = v i(old) j ηe j v u u (2.31) U jednoj iteraciji aºuriraju se svi izlazni vektori. Ukoliko je e j negativno (y j < t j ), ²to se de²ava kada je izlazna re w j prava re, a predvižena verovatno a odstupa od tih podataka, izlazni vektor re i w j pribliºava se ulaznom vektoru ulazne re i. U suprotnom se udaljava od njega. Ovom tehnikom ulazne i izlazne vektore re i iz istog konteksta pribliºavamo jedne drugima a vektore re i koje se nisu javile u istom kontekstu udaljavamo. Veli ina pomeraja zavisi od gre²ke predikcije, ²to je ve a ve i je i pomeraj. Aºuriranje ulaznih vektora re i = h j (2.32) w ij h j w ij h j = v x k w kj (2.33) k=1 Odakle je: h j = h j w ij = x i (2.34) v k=1 u k u k h j (2.35) u k = e k (2.36) u k = w jk h j (2.37) v = e k w jk h j (2.38) h = w ij = k=1 v e k vk i (2.39) k=1 v e k w jkx i (2.40) k=1 Za ulaznu re w i samo i-ta komponenta vektora x bi e jedan, ²to zna i da e samo i-ta vrsta matrice biti razli ita od nule. Podsetimo se da smo W vrste matrice W ozna ili kao ulazne vektore re i koje odgovaraju indeksu
22 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 19 vrste, ²to zna i da e u konkretnoj iteraciji biti aºuriran samo ulazni vektor ulazne re i. v vu u{new} = vu u{old} η e k vk i (2.41) Na promenu vrednosti ulaznog vektora uti u svi izlazni vektori, u meri koju odrežuje gre²ka predikcije njihovog izlaznog neurona. Ukoliko empirijski podaci pokazuju da se izlazna re w j ne nalazi kontekstu ulazne re i w i, a procenjena verovatno a pokazuje suprotno, ulazni vektor konteksne re i w i e se udaljavati od izlaznog vektora re i w j. U suprotnom e teºiti da mu se pribliºi. to je verovatno a ta nije predvižena manji e pomeraj biti. k=1 Prime ujemo da se u toku treniranja ulazni i izlazni vektori prakti no privla e ili odbijaju u zavisnosti od konteksta u kome se nalaze. Ovakav pristup o igledno postavlja re i iz istog konteksta blizu jedne drugima. Eksperimentalno je pokazano da te klastere ine semanti ki sli ne ili iste re i, ²to zapravo potvržuje Distributivnu hipotezu Kontekst od vi²e re i Model je prikazan na slici: Slika 2.11: CBOW model Vrlo je sli an modelu sa samo jednom ulaznom re i. Razlika je u izlazu iz skrivenog sloja koji je sada jednak aritmeti koj sredini ulaznih vektora re i
23 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 20 iz konteksta. Neka je C duºina konteksta.tada je izlaz iz skrivenog sloja: h = 1 C (vu u 1 + v u u v u u C ) (2.42) Izlaz iz i-tog izlanog neurona je verovatno a pojavljivanja re i u kontektsu ulaza: y i = p(w i w u1, w u2,..., w uc ) (2.43) Pri emu je vj u k ulazni vektor re i w j i k redni broj re i u kontekstu(koji je bitan samo zbog ozna avanja ina e re i mogu biti bilo kako porežane). Aºuriranje izlaznih vektora re i Potpuno identi no kao kod prozora duºine jedan : w ij = e jh i (2.44) w (new) ij v i(new) j = w (old) ij ηe j h i (2.45) = v i(old) j ηe j h (2.46) Jedina promena je u izra unavanju izlaza iz skrivenog sloja h. Aºuriranje ulaznih vektora re i Ponavljaju i postupak iz 2.30 dobijamo v = e k w w jkx i (2.47) ij k=1 Kod modela sa prozorom duºine jedan, u konkretnoj iteraciji aºurira se samo ulazni vektor ulazne re i, zbog toga ²to ulazni vektor ima jedinicu na samo jednom mestu. U ovom slu aju vektor x ima jedinicu na C mesta. Shodno tome C ulaznih vektora bi e aºurirano. v u(new) u c = v u(old) u c η v e k vk i (2.48) Model preskakanja jedinica (eng Skip-gram) Model Skip-gram arhitekura na osnovu date re i predviža re i koje je okruºuju. Za razliku od CBOW modela, sada je ciljna re ulaz a izlaz je kontekst. Model je dat na slici: k=1
24 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 21 Slika 2.12: Skip-gram model Neuronska mreºa, pa samim tim i treniranje je vrlo sli no kao kod CBOW arhitekrure. Slika 2.13: Skip-gram model Izlaz iz skrivenog sloja isti je kao kod CBOW-modela sa jednim ulazom i jednak je ulaznom vektoru ulazne re i. h = x T W = W k: = v i k (2.49) Matrice teºina izmežu skrivenog sloja i izlaza je ista za sve izlazne re i.
25 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 22 Shodno tome potencijal izlaznih neurona je: u kn = P w ikh i (2.50) i=1 Izlaz iz neurnoske mreze: u k m = P w ik h i (2.51) i=1 ako je k = k = u kn = u k m = u k (2.52) y ic = p(w ic w u ) = u k = hv i k (2.53) exp u ic v j=1 exp u j c (2.54) Pri emu je k n indeks k-tog neurona n-te konteksne re i izlaznog sloja. Za kriterijumsku funkciju, kao i kod CBOW, uzima se negativni logaritam verodostojnosti: E = log p(w p1, w p2,..., w pc w u ) = (2.55) = C exp u pc log v j=1 exp u = j c (2.56) = = c=1 c=1 C exp u pc log v j=1 exp u = (2.57) j c C log exp u pc + log c=1 = C u pc + log c=1 v exp u jc = (2.58) j=1 Pri emu je p c indeks pravog izlaza c-te konteksne re i. v exp u jc (2.59) i= Treniranje Postupak je identi an kao kod CBOW, dakle koristi se stohasti ki gradijenti spust i RBP.
26 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 23 aºuriranje izlaznih vektora re i w ij = C c=1 u jc u jc w ij (2.60) u jc w ij = h i (2.61) = ( C c=1 u p c + log v i=1 exp u i c ) = (2.62) u jc u jc = t jc + 1 v i=1 exp u i c exp u jc = (2.63) = y jc t jc = e jc (2.64) { 1 j c = p c t jc = (2.65) 0 j c p c t jc je jednak jedinici samo ako je w jc u korpusu c-ta rec u kontekstu ulazne re i. U drugom slu aju je 0. w new ij v i{new} j C w ij = e jc h i (2.66) = w old ij = v i{old} j c=1 η η C e jc h i (2.67) c=1 C e jc h (2.68) Aºuriranje ulaznih vektora re i Aºuriranje ulaznih vektora re i je identi no kao kod CBOW modela s tim ²to se sada sumiranje radi po svim kontekstnim re ima izlaznog sloja. c=1 w ij = h j h j w ij (2.69) h j = v x k w kj (2.70) k=1
27 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 24 h j = h j w ij = x i (2.71) C v c=1 k=1 u kc u kc h j (2.72) u kc = e kc (2.73) Odakle je: h j = u kc h j = w jk (2.74) C c=1 k=1 v e kc w jk (2.75) v u{new} u w ij = C c=1 k=1 C h = = v u{old} u c=1 k=1 v e kc w jkx i (2.76) v e kc vk i (2.77) η C c=1 k=1 v e kc vk i (2.78) O igledno je uzajamni uticaj ulaznih i izlaznih vektora r ci isti kao i kod CBOW modela s tim ²to je sada uslovjen gre²kama predikcije ve eg broja kontekstnih re i u izlaznom sloju Optimizacija O igledan nedostatak prethodno obja²njenih modela je sloºenost izra- unavanja. Naime, broj neurona u izlaznom sloju proporcionalan je duºini re nika. Ovi modeli prakti no su beskorisni za veliki trening skup i veliki re nik. U nastavku dajem detaljno obja²njenje optimizacionih re²enja koja se baziraju na redukciji broja izlaznih vektora koji se aºuriraju po jednoj iteraciji.
28 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR Hijerarhijski sloj izlaznih neurona(eng. Hierarchical softmax) Ideja je da umesto modelovanja verovatno e kori² enjem softmax izlaznog sloja koristimo hijerarhijski sloj gde se verovatno a pojavljivanja re i u datom kontekstu ra una na osnovu njene putanje od korena do lista kojim je predstavljena. Model koristi hijerarhijsko binarno stablo u kome su re i iz re nika predstavljene listovima. Izlazni sloj mreºe nam vi²e nije duºine re nika, sa softmax neuronima iji je izlaz jednak verovatno i pojavljvanja re i koju neuron reprezentuje, ve je jednak broju unutrasnjih cvorova stabla koji odgovaraju sigmoidalnim neuronima. Svakom unutra²njem voru pridruºena je verovatno a grananja u levo(moºe i u desno, ali kad se izabere mora da vaºi za sve neurone). Kod ovog modela vi²e nema izlazne vektorske reprezentacije re i.umesto toga svaki unutra²nji vor ima izlazni vektor v. Slika 2.14: Verovatno a pojavljivanja re i u kontekstu Iz primera vidimo da su nam za estimiranje verovatno e pojavljivanja re i potrebni samo oni neuroni koji su se na²li na putu od korena do lista kojim je predstavljena. Dakle, kompleksnost izra unavanja vi²e nije linearno proporcionalna duºini re nika ve logaritamski. O igledno je V i=1 p(w i context) = 1,gde je w j j-ta rec u re niku.
29 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR Model Slika 2.15: Hierarchical softmax model Skriveni sloj povezan je sa svim izlaznim vorovima i veze su prikazane matricom W px(v 1) gde je p veli ina skrivenog sloja. i-ta kolona matrice je jednaka izlaznom vektoru i-tog izlaznog neurona W : i = v i. Izlaz iz skrivenog sloja je h(kod CBOW h = vu u kod Skip gram h = 1 C C i=1 vu c ). Potencijal izlaznog neurona je u i = hv i.verovatno a grananja u levo u voru x p(leva grana vora x) = σ(u x ) = σ(hv i) (2.79) shodno tome, verovatno a grananja u desno je: p(desna grana vora x) = 1 σ(u x ) = σ( u x ) (2.80) Treniranje Ozna i u indeks vora na j-tom mestu na putu od korena do lista re i w sa n(w, j),sa d(w) dubinu lista,sa P (w) = {n(w, 0), n(w, 1),..., n(w, d(w) 1)}, sa levi(cvor) levo dete vora i sa [[ ]] funkciju { 1 x = tacno [[x]] = (2.81) 0 x = netacno
30 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 27 Uslovna verovatno a pojavljivanja r ci w p u datom kontekstu: p(w p kontekst) = σ([[n(w p, j + 1) = levi(n(w p, j))]]u j ) (2.82) j P (w) Radi jednostavnosti prvo emo posmatrati kontekst duºine jedan. Prelazak na vi²ekonteksni CBOW i Skip-gram je jednostavan. Za kriterijumsku funkciju uzimamo negativni logaritam verodostojnosti: E = logp(w p w u ) = log σ([[n(w p, j + 1) = levi(n(w p, j))]]u j ) j P (w) (2.83) Kao i kod CBOW i Skip-gram koristimo stohasti ki gradijent i RBP. Aºuriranje izlaznih vektora unutra²njih vorova Radi jednostavnosti [[n(w p, j + 1) = levi(n(w p, j))]] u zapisivati samo kao [[]] v j = u j u j v j (2.84) u j v j = hv j v j = h (2.85) Odakle je 1 = u j σ([[ ]]u j ) σ([[ ]]u j)(1 σ([[ ]]u j ))[[ ]] = (2.86) = (σ([[ ]]u j ) 1)[[ ]] = (2.87) { σ(u j ) 1 [[ ]] = 1 = 1 σ( u j ) = 1 (1 σ(u j )) = σ(u j ) [[ ]] = 1 = (2.88) = σ(u j ) t j (2.89) { 1 [[n(w p, j + 1) = levi(n(w p, j))]] t j = (2.90) 0 [[n(w p, j + 1) levi(n(w p, j))]] v (new) j v j = (σ(u j ) t j )h (2.91) = v (old) j η(σ(u j ) t j )h (2.92) Po jednom trening primeru aºuriraju se vektori izlaza svih vorova iji su indeksi i U(w p ), za razliku od neoptimizaovanih modela gde se aºuriraju izlazni vektori svih re i.kod Skip-gram modela postupak se ponavlja
31 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 28 za svaku re iz izlaznog konteksta. (σ(u j ) t j ) moºemo shvatiti kao gre²ku predikcije. Zadatak svakog unutra- ²njeg vora je da predvidi da li put iz njega treba da ide kroz levo ili desno dete. Ukoliko treba da ide kroz levo a on je predvideo suprotno, aºuriranjem e se njegov izlazni vektor pribliºavati vektoru h, u suprotnom e se udaljavati. Ukoliko je predikcija prili no precizna, pomeraj je mali. ºuriranje ulaznih vektora re i Kod aºuriranja ulaznih vektora razlika u odnosu na prethodne modele je samo u gradijentu izlaza skrivenog sloja, zbog sada druga ijeg izlaznog sloja. h = = log(v ) i=1 log(v ) u i u i h = (2.93) (σ(u i ) t i )v i (2.94) i= Konstrukcija hijerarhijskog stabla Postoje razli iti na ini da re nik predstavimo binarnim stablom. Kvalitet hijerarhijskog stabla uti e na ekasnost neuronske mreºe. Opisa u neke od njih: Human-ovo stablo U kome su este re i na manjoj dubini. Dokazano je da grupisanje re i iste u estanosti daje dobre rezultate u pogledu ubrzanja. Mikolov koristi ovo stablo. Slucajno generisano stablo. Generi²e se puno binarno stablo i listovi se nasumice dodeljuju re ima iz re nika. Ovakvim pristupom dobija se najmanje pobolj²anje u odnosu na softmax. Gotovo stablo. Koriste se neki gotovi lingvisti ki izvori(npr. WordNet)za dobijanje stabla. U radu [8] je obja²njeno kako se WordNet moºe iskoristiti za organizovanje re nika u hijerarhisko stablo. Tvrde da je postignuto 250x ubrzanje. Hijerarhijsko klasterovanje. Na neki na in dobijemo vektore re i, koje organizujemo u stablo algoritmom hijerarhijskog klasterovanja.
32 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR Uzimanje negativnih uzoraka (eng.negative sampling ) Ideja je da se problem estimacije verovatno a posmatra kao klasikacioni i re²ava se uz pomoc Logisti ke regresije. Radi jedostavnosti posmatramo kontekst duzine 1. Pretpostavimo da imamo skup D koji je skup svih parova (re, kontekst) koji su se javili u tekstu i skup D' parova koji se nisu javili u tekstu. D je skup pozitivnih primera a D' je skup negativnih. Cilj je da dobijemo klasikator koji paru (re,kontekst) dodeljuje labelu Z = 1 pripada skupu D i Z = 0 pripada skupu D'. Verovatno e modelujemo logisti kom funkcijom: p(z = 1 (w, c)) = exp v T wc c = (2.95) = σ(v T wc c ) (2.96) p(z = 0 (w, c)) = exp vwc T T c = (2.97) = σ( vwc T c ) (2.98) Slu ajna promenljiva Z uslovljena ulazom (w, c) ima raspodelu p(z = z (w, c)) = (σ(vwc T c ) z (1 σ(vwc T c )) 1 z (2.99) Gde su v i c vektor re i i vektor konteksta.za kriterijumsku funkciju uzimamo negativni logaritam verodostojnosti: E = log p(z = z (w, c); W, C) = (2.100) (w,c) D D = z log(σ(vwc T c )) + (2.101) (w,c) D D + (1 z) log(1 σ(vwv T c )) (2.102) = log(σ(vwc T c )) + (2.103) + (w,c) D log(1 σ(vwc T c )) (2.104) (w,c) D (2.105) Gde su W i C matrice ije su kolone redom vektori re i i vektori konteksta.
33 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR Model Na osnovu ove ideje redukuje se broj izlaznih vektora koji se aºuriraju po jednom trening primeru kod Skip-gram i CBOW modela. Ovde emo razmatrati treniranje CBOW modela (kontekst duºine jedan) kori² enjem NS. Kod Skip-grama uzorkuju se sve re i iz konteksta. U kriterijumskoj funkciji, skup pozitivnih primera sastoji se samo iz trening primera. Negativnih primera ima k i dobijaju se slu ajnim izborom ciljne re i, pod pretpostavkom da je mala verovatno a da se za tako dobijenu re par (w, c) nalazi u D. Kriterijumska funkcija je: E = log σ(vi T c c ) log σ( vwc T c ) (2.106) w W negative i je indeks ciljne re i iz trening primera c je indeks konteksta iz trening primera W negative je skup negativnih primera koji su dobijeni na osnovu empirijske 3 raspodele P (w) = freq(w) 4.Da stepenovanje daje bolje rezultate do²lo se D eksperimentalno. Neka je k broj negativnih primera. Eksperimentalno je pokazano da za male re nike k = 5do20 daje dobre rezultate a za velike k = 2do5. Minimizianjem kriterijumske funkcije maksimiziramo verovatno u da je trening par (w, c) D i da k-negativnih primera nije u skupu D. Iako je verovatno a da se nasumi no izabran primer nalazi u korpusu veoma mala, moºe se desiti da se ipak naže, zato se uzima ve i broj negativnih primera i zato broj negativnih primera opada sa veli inom re nika Treniranje Za treniranje se koristi SGD. Po jednom trening primeru aºurira se 1 konteksni vektor(konteksta iz trening primera) i k+1 vektora re i (vektor re i iz trening primera i k re i dobijenih negativnim semplovanjem). v T wc c = v w = v T wc c v T wc c v w (2.107) { σ(vwc T c ) 1 w = i (2.108) σ(vwc T c ) w W negative = σ(v T wc c ) t w (2.109)
34 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 31 t w = { 1 w = i 0 w W negative (2.110) v new w = v old w η(σ(v T wc c ) t w )c c (2.111) c c = w i W negative = (σ(v T i c c ) 1)v i + = c new c vwc T c = (2.112) vwc T c c c σ(vwc T c )v w = (2.113) w W negative w i W negative σ((v T wc c ) t w )v w (2.114) = c old c η w i W negative (σ(v T wc c ) t w )v w (2.115) O igledno je da se ovakvim treniranjem vektori re i i konteksta odbijaju i privla e u zavisnosti od toga da li je (w, c) D tj. da li su se u koprusu javili u istom kontekstu. Vi²e o ovome u radovima [9] i [10] Performanse Vi²enitno treniranje Paralelizacijom procesa treniranja postiºe se zna ajno ubrzanje. Problem je ²to moºe do i do kolizije tredova ukoliko istovremeno pristupaju vektoru iste re i. Sa pove anjem vokabulara ovakvi problemi se minimiziraju i uticaj na efektivnost je zanemarljiv Dimenzionalnost vektora Obi no oko 600 daje najbolje rezultate. Ve a dimenzionalnost uglavnom daje bolje rezultate ali to ne mora uvek da vaºi Izbor arhitekture CBOW usrednjava vrednost svih vektora iz konteksta pre nego ²to predvidi centralnu re konteksta. to ga ini manje pogodnim za nalaºenje vektora re i sa manjom u estani² u u odnosu na Skip-gram model. Ispostavilo se da model bolje nau i vektorske reprezentacije re i sa malom u estano² u ako se njihovi vektori ne usrednjavaju sa vektorima ostalih re i
35 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR 32 iz konteksta za dobijanje predikcije. Hierarchical softmax je bolji za dobijanje vektora re i male u estanosti. Razlog je ²to je kod Negative Sampling metode mala verovatno a da vektori tih re i užu u trening primere. S obzirom da se kao pozitivni primeri retko javljaju, oni e biti retko aºurirani. Kod Hierarchical softmax na vektore re i uti u svi vorovi od korena do lista, a oni e biti aºurirani svaki put kad se nažu na putu bilo koje druge re i. CBOW je brºi od Skip-gram modela i daje bolje rezultate kod velikih koprusa. Vi²e o ovome u radu [11] Veli ina prozora Konteksti manje duºine sadrºe informaciju fokusiranu na samu re, sli nost re i se bazira na sli noj funkcionalnosti. Kod ve ih prozora dobija se informacija koja se vi²e odnosi na op²tu temu, uporežuje re i sa onima koje su se javile u sli nim diskusijama. Kod Skip-gram modela naj e² e je veli ina prozora 10, kod CBOW oko Eliminisanje re i sa velikom ili malom u estano² u Re i koje su se javile zna ajno vi²e puta u korpusu u odnosu na neki prosek i duºinu korpusa, obi no daju malo informacija i to su uglavnom stopre i. Npr. lanovi u engleskom jeziku ne daju nikakvu korisnu informaciju kad se nažu u kontekstu neke re i. Zato se takve re i izbaciju iz korpusa i to pre treniranja. Mikolov koristi formulu t p(w i ) = 1 (2.116) freq(w i ) koja predstavlja verovatno u izbacivanja re i w i.t je prag, koji obi no iznosi 10 5 (dobijeno heuristi ki i daje dobre rezultate). Re i ija je u estanost pojavljivanja mala su obi no neke semanti ki nebitne re i ili je broj pojavljivanja nedovoljan za dobijanje vektorske reprezentacije re i. Mikolov izbacuje re i koje su se javile manje od pet puta. Neki eksperimenti pokazuju da ve i prag daje bolje rezultate. Re i se elimini²u pre generisanja konteksta. Izbacivanjem ovakvih re i, kontekst koji se koristi za treniranje sadrºi semanticki zna ajne re i koje nisu u okviru zadate duºine prozora ime se prakti no pove ava veli ina prozora.
36 GLAVA 2. UGRADNJA REƒI I FRAZA U VEKTORSKI PROSTOR Unapreženje Promenljiva veli ina prozora Deni²e se maksimalna duºina prozora. Zatim se za svaku re na slu- ajan na in bira veli ina prozora na osnovu diskretne uniformne raspodele U(1, max(veli ina prozora)) Nelinearni konteksti Word2vec i mnogi drugi modeli koriste liner bag of words kontekst. Postoje drugi na ini izbora konteksta. U radu [12] se predlaºe kori² enje dependecy-based konteksta (baziranih na sintaksnim relacijama mežu re- ima). Eksperimenti su pokazali da je ovakav pristup bolji za pronalaºenje funkcionalnih sli nosti dok je BOW kontekst bolji u kor² enju informacija vezanih za temu na koju se tekst odnosi. Dakle, dependecy-based konteksti se lo²e pokazuju u analogijskim testovima. Vi²e o ovome u radovima [12] i [13].
37 Glava 3 Klasterovanje Za klasterovanje dobijenih vektora je kori² en hibridni algoritam opisan u radu [14] i gotov softver. Detalji su dati u nastavku. Klasterovanje je tehnika istraºivanja podataka koja podatke deli u grupe (klastere) podataka sli nih osobina. Ovakvim postupkom skup podataka postaje pregledniji i jednostavniji za istraºivanje. Postoje mnoge metode klasterovanja i sve se, u su²tini, baziraju na tome da za ºeljeni broj klastera i funkciju za merenje rastojanja podaci podele u grupe tako da se minimizuje funkcija za merenje unutar klastera. Najve i problem kod klasterovanja je sloºenost izra unavanja i memorijskih zahteva koja je uglavnom mnogo ve a od linearne. Vektore dobijene Word2Vec modelom predstavljamo dendrogramom. Na osnovu dobijenog hijerarhijskog stabla mogu se dobiti klasteri razli ite veli ine odsecanjem stabla u odgovaraju em voru. Mežutim, zbog velikog broja vektora koje je potrebno klasterovati nemogu e je koristiti stadardan algoritam hijerarhijskog klasterovanja. Zato koristimo hibridni algritam baziran na k-means i algoritmu hijerarhisjkog klasterovanja. Naj e² e kori² ene metrike: Euklidova distanca x y 2 = i (x i y i ) 2 Pirsonov koecijent korelacije ρ x,y x.y Kosinusna sli nost ( x x )( y y ) Za algoritme klasterovanja gde se udruºuju dva supa podataka deni²e se kriterijuma povezivanja klastera, ²to predstavlja funkciju razdaljine izmežu klastera A i B: 34
38 GLAVA 3. KLASTEROVANJE 35 Maksimum ili potpuno-povezivanje max{d(x, y) : x A, y B} Minimum ili singl-povezivanje min{d(x, y) : x A, y B} 1 Sredina ili prose no povezivanje ili UPGMA A B (x,y);x A;y B d(x, y) Lance i Vilijams u radu [15] predstavljaju generalizovanu rekurentnu formulu za izra unavanje distanci izmežu novodobijenog i ostalih klastera. Neka je h klaster dobijen spajanjem klastera i i j. d(h, k) = α i d(i, k) + α j d(j, k) + βd(i, j) + γ d(i, k) d(j, k) (3.1) Parametri odrežuju kriterijum povezivanja. Vrednosti parametara za pomenute kriterijume: Kriterijum povezivanja α i α j β γ Maksimum 1/2 1/2 0 1/2 Minimum 1/2 1/2 0 1/2 n i n i UPGMA 0 0 n i + n j n i + n j n x kardinalnost klastera x. 3.1 Hibridni algoritam Ovaj algoritam sastoji se iz dva koraka. U prvom koraku, podaci se grupi²u k-mean algoritmom u klastere P i. Drugi korak se sastoji iz dva nivoa. U prvom nivou se podaci iz tako dobijenih klastera grupi²u aglomerativnim hijerarhijskim algoritmom (AHC) u stabla T i. Ukoliko je veli ina klastera >20000, hibridni algoritam se rekurzivno primenjuje na taj klaster. U drugom nivou se dobijena stabla tretiraju kao listovi i na njih se primenjuje AHC. Distance izmežu k-klastera dobijenih u prvom koraku se dobijaju: { d(c 1, C 2 ) (R 1, R 2 ) + d NN (P 1 ) + d NN (P 2 ) ako je d(c 1, C 2 ) (R 1, R 2 ) > 0 d(p 1, P 2 ) = max(d NN (P 1 ), d NN (P 2)) (3.2) Gde je C x centroid P x klastera, d nn (P i )je srednja vrednost najbliºih suseda unutar komponente P i,r i polupre nik klastera Formula je dobijena na osnovu ideje o data bubbles opisane u radu [16]. Intuitivno, funkcija razdaljine aproksimira udaljenost dve najbliºe ta ke para
39 GLAVA 3. KLASTEROVANJE 36 klastera. Ovakvim izra unavanjaem u situaciji u kojoj imamo parove požednako udaljenih klastera, gde prvi par ima mali precnik a drugi par veliki i klasteri se moºda poklapaju, drugi par se smatra blizim. Moºe da se desi da razdaljina izmežu dva klastera bude manja nego polupre nik neke od njih. Zato deni²emo okida r i tako da se sve ta ke klastera P i na rastojanju od centra daljem od r i izbacuju iz klastera i posmatraju kao zasebne komponente Ekasnost i efektivnost Sloºenost izra unavanja zavisi od sloºenosti k-mean algoritma i AHC algoritma. Standardni k-mean algoritam ima sloºenost o(kn L) pri emu je k-broj klastera, N broj podatak i L broj iteracija. Koriste i se radom [17], izra unavanje udaljenosti svih ta aka od svih centroida se izvr²ava u svega nekoliko iteracija. Zato je broj izra unavanja distanci blizi kn nego knl. Dakle sloºenost prvog koraka je o(knl )gde je L << L i moze biti estimirano eksperimentalno. Eksperimenti pokazuju da se L kre e od 2-5. Kao aglomerativni algortam hijerarhuskog klasterovanja koristimo,algoritam lanaca najbliºih suseda (Nearest-neighbor chain algorithm) ija je kompleksnost izra unavanja za N ulaznih podataka o(n 2 ). Prostorna sloºenost i iznosi o(n). Kompleksnost drugog koraka uklju uje kompleksnost hijerarhijskog klasterovanja k skupova od pribliºno N/k elemenata i kompleksnost hijerarhijskog klasterovanja k centroida. Dakle, o(k 2 +kn 2 /k 2 ) = o(k 2 +N 2 /k).knl dominira nad k 2 pa je sloºenost kompletnog algoritma o(n 2 /k+knl). Najbolji rezultati se postiºu za takvo k = (N) kada je kompleksnost o(n N). Sli na izra unavanja dovode do iste memorijske sloºenosti. Treba biti paºljiv pri izboru k, ukoliko je premalo, moze da se desi da se sli ni objekti odvoje u prvim fazama klasterovanja ²to dovodi do lo²e lokalne tacnosti. Ukoliko je preveliko, smanjuje se ekasnost algoritma i ta nost na globalnom nivou( svi klasteri se posmatraju kao listovi i udruºuju se samo koreni dobijenih stabala(ne moºe se desiti da se stabla nadoveºu). U pogledu brzine klastervanja, hibridni algoritam nadvladava AHC sa pove- anjem broja podataka. Za manje skupove podataka bolje je koristiti AHC. Na osnovu eksperimenata utvrženo je da daje pribliºno iste rezultate kao AHC.
40 GLAVA 3. KLASTEROVANJE Klasterizacija metodom k-srednjih vrednosti (eng K-means) K-mean je naj e² e kori² en algoritam klasterovanja zbog male sloºenosti. Naime nije potrebno izra unavati razdaljine izmežu svih podataka u svakom koraku. Kompleksnost izra unavanja je o(knl) gde je k broj klastera, n broj podataka i l broj iteracija Ubrzanje Algoritam je ražen na osnovu rada [17]. Ideja za ubrzanje leºi u tome da nije potrebno u svakoj iteraciji ra unati udaljenost svih ta aka od svih centara. Ako je ta ka jako udaljena od centra ili je mnogo bliºa nego drugim centrima, nema potrebe za izra unavanjem ta nih udaljenosti. Ovaj algoritam za proizvoljne inicijalne centre na kraju daje iste centre kao i k-means i radi sa proizvoljnom metrikom. Algoritam se bazira na nejednakosti trougla d(x, z) < d(x, y) + d(y, z) (3.3) Koristimo i dve leme iji se dokaz bazira na nejednakosti trougla. Lemma 1. Neka je x ta ka i c i c centri. Ako je d(c, c) >= 2d(x, c) onda je d(x, c ) d(x, c) Dokaz. Iz nejednakosti trougla znamo da je d(c, c ) d(c, x) + d(x, c) pa je d(c, c ) d(x, c) d(x, c ). Primenjuju i uslov dobijamo d(c, c ) d(c, x) 2d(x, c) d(x, c) = d(x, c) = d(x, c ) d(x, c) Lemma 2. Neka je x ta ka i c i m(c) centri. Onda je d(x, m(c)) >= max{0, d(x, c) d(c, m(c))} Dokaz. Iz nejednakosti trougla znamo da je d(x, m(c)) d(x, c) d(c, m(c)) takože je d(x, m(c)) 0 Koriste i ove dve leme, ve inu podataka iz jedne iteracije koristimo u narednoj ime smanjujemo sloºenost operacija. Takože, pre konkretnih izra unavanja razdaljina postavljamo uslove kojima elimini²emo ve inu podataka iz daljeg razmatranja. Uslovi se baziraju na razdaljinama izmežu centara, ²to znatno smanjuje broj izra unavanja u odnosu na algoritme koji se baziraju na razdaljinama izmežu podataka. Postupak je slede i: Na po etku se inicijalizuju centri c i svakoj ta ki x se dodeli najbliºi klaster c(x) = argmin c d(x, c). Koristimo lemu 1 da bismo smanjili izra unavanja.
41 GLAVA 3. KLASTEROVANJE 38 Sa l(x, c) = d(x, c), odnosno l(x, c) = 0 ako d(x, c) nije izra unato, ozna avamo donju granicu rastojanja ta ke x od centra c(sigurno znamo da nije na manjem rastojanju). Sa u(x) = d(x, c(x)) ozna avamo gornju granicu udaljenosti ta ke x od centra klastera kome pripada (sigurno nije na ve em rastojanju). U svakoj iteraciji se za svaki par centara c i c' izra una distanca d(c, c ) i minimalna distanca s(c) = 1min 2 c c d(c, c ). Koriste i lemu 1 elimini²emo sve ta ke za koje je u(x) < s(c) (jer je udaljenost tih ta aka od centra klastera kome pripada manja od udaljenosti od centara ostalih klastera) iz daljeg razmatranja u trenutnoj iteraciji. Za preostale podatke x: Ukoliko za klaster c c(x) je u(x) l(x, c) ili u(x) 1 d(c(x), c) zaklju- 2 ujemo da ta ka x ne pripada klasteru c i nastaviljamo proveru za druge klastere. Ukoliko nijedan uslov nije ispunjen, proveravamo uslove za pravu razdaljinu d(x,c(x))(koju tek sad ra unamo) umesto u(x). Ukoliko nijedan nije ispunjen kona no ra unamo d(x,c), uporežujemo sa d(x,c(x)) i x dodeljujemo klasteru c ako je potrebno. Na kraju svake iteracije ra unamo nove centre m(x) i aºuriramo gornje i donje granice. l(x, m(c)) = max(l(x, c) d(c, m(c)), 0)(lema 2.) (3.4) u(x) = u(x) + d(m(c(x)), c(x)) (3.5) Zbog izra unavanja funkcije l kompleksnost ostaje najmanje o(knl) iako je smanjena kompleksnost izra unavanja distanci na o(n). Ovaj algoritam toliko smanjuje broj izra unavanja distanci da se vi²e vremena tro²i na odr- ºavanje pomo nih podataka. I pored toga, ukupno vreme izvr²enja znatno je manje nego kod obi nog k-mean algoritma. Sa pove anjem k i L(broja iteracija) broj izra unavanja distanci raste vrlo malo, tako da je sloºenost prbliºnija O(n) nego O(knL). Algoritam ostaje efektivan i za podatke velike dimenzionalnosti Aglomerativno hijerarhijsko klasterovanje Svi metodi klasterovanja se baziraju na razdaljini izmežu podataka koji se klasteruju. Informacije o distanci izmežu podataka se dostavljaju na dva na ina. U prvom pristupu se koristi matrica distanci D, dimenzija nxn (n- broj podataka koji se klasteruju), gde je D x,y = d(x, y). d(x, y) je mera rastojanja izmdeju objekata x i y. Nakon svake iteracije u matricu se upisuju rastojanja od novog do ostalih klastera.
42 GLAVA 3. KLASTEROVANJE 39 U drugom pristupu je svaki objekat predstavljen kao ta ka u k-dimenzionom prostoru i denisana je metrika za uporeživanje ovih vektora. Koristi se centroidna strategija u kojoj se spojeni klasteri zamenjuju jednom ta kom. Najjednostavniji algoritmi se sastoje iz slede ih koraka: Za n ulaznih podataka izra unati matricu rastojanja D nxn zatim ponoviti korake 1 i 2 n puta: 1. Na i najmanje rastojanje d(i, j) u datoj matrici D 2. Izra unati potrebna rastojanja izmežu novog klastera i ostalih klastera i aºurirati matricu D Sloºenost prvog koraka je o igledno o(n 2 ), drugog o(n). Dakle, sloºenost izra unavanja ovakvog algoritma je o(n 3 ). Da bismo smanjili sloºenost, koristimo algoritam Lanaca najbliºih suseda (eng. Nearest-neighbor chain algorithm) Lanac najbliºih suseda Ideja algoritma je da se prati put najbliºih suseda i kada se dože do podataka koji su uzajamno najbliºi oni se klasteruju. Ovakvim algoritmom dobija se isto hijerarhisko stablo kao i standardnim algoritmom s tim ²to se klasteri spajaju u druga ijem redosledu. Neka je n broj ulaznih podataka koji pripadaju skupu D. Koristimo stek za uvanje putanje. Algoritam se sastoji iz slede ih koraka: 1. Uzeti element C sa vrha steka. Ukoliko je prazan uzeti proizvoljni element iz skupa D. 2. Na i najbliºi sused elementa C iz D. 3. Ukoliko je ve u steku, zna i da je C njegov najbliºi sused.u tom slu- aju podaci se izbacuju iz steka, klasteruju i vra aju u skup D. U suprotnom sused se ubacuje u stek. Kada je D = 1 prestaje se sa radom Sloºenost Klastera ima koliko listova i unutra²njih vorova stabla (koren se ne ra- una). Dakle 2n 2. Za pretragu najbliºih suseda izvr²eno je najvi²e n-1 operacija za svaki klaster ²to dovodi do ukupne slozenosti o(n 2 ).
43 Glava 4 Obrada podataka Za dobijanje podataka iz hijerarhijskog stabla koristimo dve re i(ili fraze) kao semena. Stablo se emo u njihovom najblizem pretku i dobijamo klaster koji ih sadrºi. Istraºuju i ovako dobijene skupove nalazimo re i koje su manje poznate korisnicima a semanti ki su sli ne ulazima(semenima). Postoje mnogi na ini za dobijanje podataka iz stabla ili iz semanti kog prostora. Mogu se koristiti osobine vektorskog prostora i ekstrakovati podaci operacijama nad vektorima, da se deni²e neka okolina vektora iz koje emo pokupiti podatke... Ovde primenjena tehnologija dala je dobre rezultate i radi vrlo brzo. Vrlo je povoljan alat za osveºavanje gotovih listi novim podacima. Npr. sistem moºe da dopunjava listu aktivnih programskih jezika, ve²tina, alata, da popunjava listu novih lmova, pesama tako ²to e da obražuje nove podatke koji se svakodnevno objavljuju na internetu Se enje stabla Rastojanja u stablu odgovaraju semanti kim sli nostima izmežu re i koje su predstavljene kao listovi. Prou avaju i veze u stablu prime uje se da se se enjem stabla u odgovaraju em voru dobija skup semanti ki sli nih re i ija sli nost opada sa visinom presecaju eg vora. Svaki vor stabla predstavljamo binarnim kodom koji predstavlja putanju od korena do njega(bit najve e teºine ozna ava skretanje u korenu)i dubinom d. Jedinica je indikator za grananje u levo, nula za desno. Za date ulazne re i (i,j) neka su (x i, x j ) njihovi binarni kodovi i (d i, d j ) dubine. Primenimo XOR operaciju na kodove koji sadrºe prvih d bitova najve e teºine,gde je d = min(d i, d j ) da dobijemo dubinu prvog zajedni kog pretka. Dubinu ozna avamo sa dp. Da bismo nasli prvog zajedni kog pretka kre emo se od korena po putanji x i ili x j do dubine dp. Binarne kodove 40
44 GLAVA 4. OBRADA PODATAKA 41 listova dobijenih odsecanjem stabla u nekom voru dobijamo kao sve mogu e kombinacije preostalih bitova od njega do kraja stabla Vizuelizacija i rezultati U korpusu rezimea i ponuda za posao smo, primenom PMI algoritma, detektovali smo fraze. Zatim smo dobijeni tekst trenirali CBOW modelom i dobili vektore re i i fraza koje smo klasterovali hibridnim algoritmom. Za vizuelizaciju koristimo program koji se moºe na i na adresi Program TreeView nam omogu ava manipulaciju stablom, uveli avanje i udaljavanje, odsecanje stabla u odgovaraju em voru kao i prikazivanje proizvoljnog broja najbliºih suseda neke re i, ²to daje brz uvid u kvalitet klasterovanja. Primer: Slika 4.1: Dendrogram
Univerzitet u Ni²u Prirodno - matemati ki fakultet Departman za matematiku KLASTER ANALIZA U STATISTIƒKOM ZAKLjUƒIVANjU Master rad Student: Katarina M
 Univerzitet u Ni²u Prirodno - matemati ki fakultet Departman za matematiku KLASTER ANALIZA U STATISTIƒKOM ZAKLjUƒIVANjU Master rad Student: Katarina M. Krsti Mentor: Prof. dr Aleksandar S. Nasti br. indeksa
Univerzitet u Ni²u Prirodno - matemati ki fakultet Departman za matematiku KLASTER ANALIZA U STATISTIƒKOM ZAKLjUƒIVANjU Master rad Student: Katarina M. Krsti Mentor: Prof. dr Aleksandar S. Nasti br. indeksa
LINEARNA ALGEBRA 2 Popravni kolokvij srijeda, 13. velja e Zadatak 1. ( 7 + 5=12 bodova) Zadan je potprostor L = {(x 1, x 2, x 3, x 4 ) C 4 : x 1
 Zadatak 1. ( 7 + 5=12 bodova) Zadan je potprostor L = {(x 1, x 2, x, x 4 ) C 4 : x 1 + x 2 + x = 0, x 1 = 2x 2 } unitarnog prostora C 4 sa standardnim skalarnim produktom i vektor v = (2i, 1, i, ) C 4.
Zadatak 1. ( 7 + 5=12 bodova) Zadan je potprostor L = {(x 1, x 2, x, x 4 ) C 4 : x 1 + x 2 + x = 0, x 1 = 2x 2 } unitarnog prostora C 4 sa standardnim skalarnim produktom i vektor v = (2i, 1, i, ) C 4.
3. Neprekinute funkcije U ovoj to ki deniramo neprekinute funkcije. Slikovito, graf neprekinute funkcije moºemo nacrtati a da ne diºemo olovku s papir
 3. Neprekinute funkcije U ovoj to ki deniramo neprekinute funkcije. Slikovito, graf neprekinute funkcije moºemo nacrtati a da ne diºemo olovku s papira. Neprekinute funkcije vaºne su u teoriji i primjenama.
3. Neprekinute funkcije U ovoj to ki deniramo neprekinute funkcije. Slikovito, graf neprekinute funkcije moºemo nacrtati a da ne diºemo olovku s papira. Neprekinute funkcije vaºne su u teoriji i primjenama.
Seminar peti i ²esti U sljede a dva seminara rije²avamo integrale postavljene u prosturu trostruke integrale. Studenti vjeºbom trebaju razviti sposobn
 Seminar peti i ²esti U sljede a dva seminara rije²avamo integrale postavljene u prosturu trostruke integrale. Studenti vjeºbom trebaju razviti sposobnost vizualizacije dijela prostora i skiciranja dvodimenzionalnih
Seminar peti i ²esti U sljede a dva seminara rije²avamo integrale postavljene u prosturu trostruke integrale. Studenti vjeºbom trebaju razviti sposobnost vizualizacije dijela prostora i skiciranja dvodimenzionalnih
Mere slicnosti
 Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
Seminar 13 (Tok funkcije) Obavezna priprema za seminar nalazi se na drugoj stranici ovog materijala. Ove materijale obražujemo na seminarima do kraja
 Seminar 13 (Tok funkcije) Obavezna priprema za seminar nalazi se na drugoj stranici ovog materijala. Ove materijale obražujemo na seminarima do kraja semestra. Potrebno predznanje Ovaj seminar saºima sva
Seminar 13 (Tok funkcije) Obavezna priprema za seminar nalazi se na drugoj stranici ovog materijala. Ove materijale obražujemo na seminarima do kraja semestra. Potrebno predznanje Ovaj seminar saºima sva
Univerzitet u Ni²u Prirodno - matemati ki fakultet Departman za matematiku Linearni regresioni modeli u nansijama Master rad Mentor: dr Aleksandar Nas
 Univerzitet u Ni²u Prirodno - matemati ki fakultet Departman za matematiku Linearni regresioni modeli u nansijama Master rad Mentor: dr Aleksandar Nasti Student: Aleksandra Cvetanovi Ni², 2015. Sadrºaj
Univerzitet u Ni²u Prirodno - matemati ki fakultet Departman za matematiku Linearni regresioni modeli u nansijama Master rad Mentor: dr Aleksandar Nasti Student: Aleksandra Cvetanovi Ni², 2015. Sadrºaj
PowerPoint Presentation
 Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica
 Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
TEORIJA SIGNALA I INFORMACIJA
 Multiple Input/Multiple Output sistemi MIMO sistemi Ulazi (pobude) Izlazi (odzivi) u 1 u 2 y 1 y 2 u k y r Obrada=Matematički model Načini realizacije: fizički sistemi (hardware) i algoritmi (software)
Multiple Input/Multiple Output sistemi MIMO sistemi Ulazi (pobude) Izlazi (odzivi) u 1 u 2 y 1 y 2 u k y r Obrada=Matematički model Načini realizacije: fizički sistemi (hardware) i algoritmi (software)
PowerPoint Presentation
 Факултет организационих наука Центар за пословно одлучивање Системи за препоруку П8: Системи за препоруку Закључивање на основу случајева Системи за препоруку 2 Закључивање на основу случајева ПРОНАЂЕНО
Факултет организационих наука Центар за пословно одлучивање Системи за препоруку П8: Системи за препоруку Закључивање на основу случајева Системи за препоруку 2 Закључивање на основу случајева ПРОНАЂЕНО
Z A K O N O SUDSKIM VEŠTACIMA I. UVODNE ODREDBE lan 1. Ovim zakonom ure uju se uslovi za obavljanje vešta enja, postupak imenovanja i razrešenja sudsk
 Z A K O N O SUDSKIM VEŠTACIMA I. UVODNE ODREDBE lan 1. Ovim zakonom ure uju se uslovi za obavljanje vešta enja, postupak imenovanja i razrešenja sudskih veštaka (u daljem tekstu: veštak), postupak upisa
Z A K O N O SUDSKIM VEŠTACIMA I. UVODNE ODREDBE lan 1. Ovim zakonom ure uju se uslovi za obavljanje vešta enja, postupak imenovanja i razrešenja sudskih veštaka (u daljem tekstu: veštak), postupak upisa
P11.3 Analiza zivotnog veka, Graf smetnji
 Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe
 6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe, očekuje se da su koordinate celobrojne. U slučaju
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe, očekuje se da su koordinate celobrojne. U slučaju
ПА-4 Машинско учење-алгоритми машинског учења
 ПА-4 Машинско учење-алгоритми машинског учења Машинско учење увод и основни појмови Деф: the desgn and development of algorthms that allow computers to mprove ther performance over tme based on data sensor
ПА-4 Машинско учење-алгоритми машинског учења Машинско учење увод и основни појмови Деф: the desgn and development of algorthms that allow computers to mprove ther performance over tme based on data sensor
Osnovni pojmovi teorije verovatnoce
 Osnovni pojmovi teorije verovatnoće Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2019 Milan Merkle Osnovni pojmovi ETF Beograd 1 / 13 Verovatnoća i statistika:
Osnovni pojmovi teorije verovatnoće Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2019 Milan Merkle Osnovni pojmovi ETF Beograd 1 / 13 Verovatnoća i statistika:
Орт колоквијум
 II колоквијум из Основа рачунарске технике I - 27/28 (.6.28.) Р е ш е њ е Задатак На улазе x, x 2, x 3, x 4 комбинационе мреже, са излазом z, долази четворобитни BCD број. Ако број са улаза при дељењу
II колоквијум из Основа рачунарске технике I - 27/28 (.6.28.) Р е ш е њ е Задатак На улазе x, x 2, x 3, x 4 комбинационе мреже, са излазом z, долази четворобитни BCD број. Ако број са улаза при дељењу
Microsoft Word - AIDA2kolokvijumRsmerResenja.doc
 Konstrukcija i analiza algoritama 2 (prvi kolokvijum, smer R) 1. a) Konstruisati AVL stablo od brojeva 100, 132, 134, 170, 180, 112, 188, 184, 181, 165 (2 poena) b) Konkatenacija je operacija nad dva skupa
Konstrukcija i analiza algoritama 2 (prvi kolokvijum, smer R) 1. a) Konstruisati AVL stablo od brojeva 100, 132, 134, 170, 180, 112, 188, 184, 181, 165 (2 poena) b) Konkatenacija je operacija nad dva skupa
Рачунарска интелигенција
 Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Skripte2013
 Chapter 2 Algebarske strukture Preslikivanje f : A n! A se naziva n-arna operacija na skupu A Ako je n =2, kažemo da je f : A A! A binarna operacija na A Kažemo da je operacija f arnosti n, u oznaci ar
Chapter 2 Algebarske strukture Preslikivanje f : A n! A se naziva n-arna operacija na skupu A Ako je n =2, kažemo da je f : A A! A binarna operacija na A Kažemo da je operacija f arnosti n, u oznaci ar
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K.
 1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K. Elementi a k K su koeficijenti polinoma P (x). Ako
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K. Elementi a k K su koeficijenti polinoma P (x). Ako
DR DRAGOŚ CVETKOVIC DR SLOBODAN SIMIC DISKRETNA MATEMATIKA MATEMATIKA ZA KOMPJUTERSKE NAUKĘ DRUGO ISPRAYLJENO I PROSIRENO IZDANJE HMUJ
 DR DRAGOŚ CVETKOVIC DR SLOBODAN SIMIC DISKRETNA MATEMATIKA MATEMATIKA ZA KOMPJUTERSKE NAUKĘ DRUGO ISPRAYLJENO I PROSIRENO IZDANJE HMUJ Sadrżaj Predgovor Iz predgovora prvoni izdanju knjige "Diskretne mateiuatićke
DR DRAGOŚ CVETKOVIC DR SLOBODAN SIMIC DISKRETNA MATEMATIKA MATEMATIKA ZA KOMPJUTERSKE NAUKĘ DRUGO ISPRAYLJENO I PROSIRENO IZDANJE HMUJ Sadrżaj Predgovor Iz predgovora prvoni izdanju knjige "Diskretne mateiuatićke
Veeeeeliki brojevi
 Matematička gimnazija Nedelja informatike 3 12. decembar 2016. Uvod Postoji 10 tipova ljudi na svetu, oni koji razumeju binarni sistem, oni koji ne razumeju binarni sistem i oni koji nisu očekivali šalu
Matematička gimnazija Nedelja informatike 3 12. decembar 2016. Uvod Postoji 10 tipova ljudi na svetu, oni koji razumeju binarni sistem, oni koji ne razumeju binarni sistem i oni koji nisu očekivali šalu
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Ivana Šore REKURZIVNOST REALNIH FUNKCIJA Diplomski rad Voditelj rada: doc.
 SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Ivana Šore REKURZIVNOST REALNIH FUNKCIJA Diplomski rad Voditelj rada: doc.dr.sc. Zvonko Iljazović Zagreb, rujan, 2015. Ovaj diplomski
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Ivana Šore REKURZIVNOST REALNIH FUNKCIJA Diplomski rad Voditelj rada: doc.dr.sc. Zvonko Iljazović Zagreb, rujan, 2015. Ovaj diplomski
Inženjering informacionih sistema
 Fakultet tehničkih nauka, Novi Sad Inženjering informacionih sistema Dr Ivan Luković Dr Slavica Kordić Nikola Obrenović Milanka Bjelica Dr Jelena Borocki Dr Milan Delić UML UML (Unified Modeling Language)
Fakultet tehničkih nauka, Novi Sad Inženjering informacionih sistema Dr Ivan Luković Dr Slavica Kordić Nikola Obrenović Milanka Bjelica Dr Jelena Borocki Dr Milan Delić UML UML (Unified Modeling Language)
LAB PRAKTIKUM OR1 _ETR_
 UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA, TELEKOMUNIKACIJE I RAČUNARI PREDMET: OSNOVE RAČUNARSTVA 1 FOND ČASOVA: 2+1+1 LABORATORIJSKA VJEŽBA BROJ 1 NAZIV: REALIZACIJA
UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA, TELEKOMUNIKACIJE I RAČUNARI PREDMET: OSNOVE RAČUNARSTVA 1 FOND ČASOVA: 2+1+1 LABORATORIJSKA VJEŽBA BROJ 1 NAZIV: REALIZACIJA
Microsoft Word _Vipnet_komentar_BSA_final.doc
 Zagreb, 21.11.2011. Hrvatska agencija za poštu i elektroni ke komunikacije Juriši eva 13 HR-10 000 ZAGREB PREDMET: Javna rasprava - Prijedlog odluke kojom se HT-u odre uju izmjene i dopune Standardne ponude
Zagreb, 21.11.2011. Hrvatska agencija za poštu i elektroni ke komunikacije Juriši eva 13 HR-10 000 ZAGREB PREDMET: Javna rasprava - Prijedlog odluke kojom se HT-u odre uju izmjene i dopune Standardne ponude
P1.1 Analiza efikasnosti algoritama 1
 Analiza efikasnosti algoritama I Asimptotske notacije Master metoda (teorema) 1 Asimptotske notacije (1/2) Služe za opis vremena izvršenja algoritma T(n) gde je n N veličina ulaznih podataka npr. br. elemenata
Analiza efikasnosti algoritama I Asimptotske notacije Master metoda (teorema) 1 Asimptotske notacije (1/2) Služe za opis vremena izvršenja algoritma T(n) gde je n N veličina ulaznih podataka npr. br. elemenata
Slide 1
 Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
IErica_ActsUp_paged.qxd
 Dnevnik šonjavka D`ef Kini Za D`u li, Vi la i Gran ta SEP TEM BAR P o n e d e l j a k Pret po sta vljam da je ma ma bi la a vol ski po no - sna na sa mu se be {to me je na te ra la da pro - {le go di ne
Dnevnik šonjavka D`ef Kini Za D`u li, Vi la i Gran ta SEP TEM BAR P o n e d e l j a k Pret po sta vljam da je ma ma bi la a vol ski po no - sna na sa mu se be {to me je na te ra la da pro - {le go di ne
Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]
![Microsoft PowerPoint - 03-Slozenost [Compatibility Mode] Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]](/thumbs/102/154806426.jpg) Сложеност алгоритама (Програмирање 2, глава 3, глава 4-4.3) Проблем: класа задатака истог типа Велики број различитих (коректних) алгоритама Величина (димензија) проблема нпр. количина података које треба
Сложеност алгоритама (Програмирање 2, глава 3, глава 4-4.3) Проблем: класа задатака истог типа Велики број различитих (коректних) алгоритама Величина (димензија) проблема нпр. количина података које треба
Osnovi programiranja Beleške sa vežbi Smer Računarstvo i informatika Matematički fakultet, Beograd Jelena Tomašević i Sana Stojanović November 7, 2005
 Osnovi programiranja Beleške sa vežbi Smer Računarstvo i informatika Matematički fakultet, Beograd Jelena Tomašević i Sana Stojanović November 7, 2005 2 Sadržaj 1 5 1.1 Specifikacija sintakse programskih
Osnovi programiranja Beleške sa vežbi Smer Računarstvo i informatika Matematički fakultet, Beograd Jelena Tomašević i Sana Stojanović November 7, 2005 2 Sadržaj 1 5 1.1 Specifikacija sintakse programskih
Matrice. Algebarske operacije s matricama. - Predavanje I
 Matrice.. Predavanje I Ines Radošević inesr@math.uniri.hr Odjel za matematiku Sveučilišta u Rijeci Matrice... Matrice... Podsjeti se... skup, element skupa,..., matematička logika skupovi brojeva N,...,
Matrice.. Predavanje I Ines Radošević inesr@math.uniri.hr Odjel za matematiku Sveučilišta u Rijeci Matrice... Matrice... Podsjeti se... skup, element skupa,..., matematička logika skupovi brojeva N,...,
Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odr
 Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odrediti njene krajeve. b) Odrediti sledeće skupove: -
Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odrediti njene krajeve. b) Odrediti sledeće skupove: -
Algoritmi i arhitekture DSP I
 Univerzitet u Novom Sadu Fakultet Tehničkih Nauka Katedra za računarsku tehniku i međuračunarske komunikacije Algoritmi i arhitekture DSP I INTERNA ORGANIACIJA DIGITALNOG PROCESORA A OBRADU SIGNALA INTERNA
Univerzitet u Novom Sadu Fakultet Tehničkih Nauka Katedra za računarsku tehniku i međuračunarske komunikacije Algoritmi i arhitekture DSP I INTERNA ORGANIACIJA DIGITALNOG PROCESORA A OBRADU SIGNALA INTERNA
Paper Title (use style: paper title)
 Статистичка анализа коришћења електричне енергије која за последицу има примену повољнијег тарифног става Аутор: Марко Пантовић Факултет техничких наука, Чачак ИАС Техника и информатика, 08/09 e-mal адреса:
Статистичка анализа коришћења електричне енергије која за последицу има примену повољнијег тарифног става Аутор: Марко Пантовић Факултет техничких наука, Чачак ИАС Техника и информатика, 08/09 e-mal адреса:
Microsoft PowerPoint - Programski_Jezik_C_Organizacija_Izvornog_Programa_I_Greske [Compatibility Mode]
![Microsoft PowerPoint - Programski_Jezik_C_Organizacija_Izvornog_Programa_I_Greske [Compatibility Mode] Microsoft PowerPoint - Programski_Jezik_C_Organizacija_Izvornog_Programa_I_Greske [Compatibility Mode]](/thumbs/104/162384614.jpg) Programski jezik C organizacija izvornog programa Prevođenje Pisanje programa izvorni program Prevođenje programa izvršni program Izvršavanje programa rezultat Faze prevođenja Pretprocesiranje Kompilacija
Programski jezik C organizacija izvornog programa Prevođenje Pisanje programa izvorni program Prevođenje programa izvršni program Izvršavanje programa rezultat Faze prevođenja Pretprocesiranje Kompilacija
Орт колоквијум
 Испит из Основа рачунарске технике - / (6.6.. Р е ш е њ е Задатак Комбинациона мрежа има пет улаза, по два за број освојених сетова тенисера и један сигнал који одлучује ко је бољи уколико је резултат
Испит из Основа рачунарске технике - / (6.6.. Р е ш е њ е Задатак Комбинациона мрежа има пет улаза, по два за број освојених сетова тенисера и један сигнал који одлучује ко је бољи уколико је резултат
Univerzitet u Niˇ su ˇki Fakultet Prirodno matematic ˇunarske nauke Departman za rac Uˇ cenje vektorske reprezentacije reˇ ci govornog jezika primenom
 Univerzitet u Niˇ su ˇki Fakultet Prirodno matematic ˇunarske nauke Departman za rac Uˇ cenje vektorske reprezentacije reˇ ci govornog jezika primenom dubokih neuronskih mreˇ za Master rad Mentor: Prof.
Univerzitet u Niˇ su ˇki Fakultet Prirodno matematic ˇunarske nauke Departman za rac Uˇ cenje vektorske reprezentacije reˇ ci govornog jezika primenom dubokih neuronskih mreˇ za Master rad Mentor: Prof.
Model podataka
 Fakultet organizacionih nauka Uvod u informacione sisteme Doc. Dr Ognjen Pantelić Modeliranje podataka definisanje strategije snimanje postojećeg stanja projektovanje aplikativno modeliranje implementacija
Fakultet organizacionih nauka Uvod u informacione sisteme Doc. Dr Ognjen Pantelić Modeliranje podataka definisanje strategije snimanje postojećeg stanja projektovanje aplikativno modeliranje implementacija
PowerPoint Presentation
 Nedjelja 6 - Lekcija Projiciranje Postupci projiciranja Projiciranje je postupak prikazivanja oblika nekog, u opštem slučaju trodimenzionalnog, predmeta dvodimenzionalnim crtežom. Postupci projiciranja
Nedjelja 6 - Lekcija Projiciranje Postupci projiciranja Projiciranje je postupak prikazivanja oblika nekog, u opštem slučaju trodimenzionalnog, predmeta dvodimenzionalnim crtežom. Postupci projiciranja
1
 Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
GENETSKI TREND PRINOSA MLEKA I MLEČNE MASTI U PROGENOM TESTU BIKOVA ZA VEŠTAČKO OSEMENJAVANJE
 IV SEMINAR ODGAJIVAČKIH ORGANIZACIJA U STOČARSTVU REPUBLIKE SRBIJE HOTEL ĐERDAP TURIST 01.- 04. April 2018. Procena oplemenjivačkih vrednosti u stočarstvu ES( G) h 2 i L r IH Prof. dr Snežana Trivunović,
IV SEMINAR ODGAJIVAČKIH ORGANIZACIJA U STOČARSTVU REPUBLIKE SRBIJE HOTEL ĐERDAP TURIST 01.- 04. April 2018. Procena oplemenjivačkih vrednosti u stočarstvu ES( G) h 2 i L r IH Prof. dr Snežana Trivunović,
Klasifikacija slika kucnih brojeva dubokim konvolucijskim modelima
 Klasifikacija slika kućnih brojeva dubokim konvolucijskim modelima Ivan Šego 4. srpnja 2018. Sadržaj 1 Uvod 2 Konvolucijske neuronske mreže Konvolucijski sloj Sloj sažimanja Potpuno povezani sloj 3 Ispitni
Klasifikacija slika kućnih brojeva dubokim konvolucijskim modelima Ivan Šego 4. srpnja 2018. Sadržaj 1 Uvod 2 Konvolucijske neuronske mreže Konvolucijski sloj Sloj sažimanja Potpuno povezani sloj 3 Ispitni
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић
 Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Драган Пејић, Бојан Вујичић, Небојша Пјевалица,
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Драган Пејић, Бојан Вујичић, Небојша Пјевалица,
Увод у организацију и архитектуру рачунара 1
 Увод у организацију и архитектуру рачунара 2 Александар Картељ kartelj@matf.bg.ac.rs Напомена: садржај ових слајдова је преузет од проф. Саше Малкова Увод у организацију и архитектуру рачунара 2 1 Секвенцијалне
Увод у организацију и архитектуру рачунара 2 Александар Картељ kartelj@matf.bg.ac.rs Напомена: садржај ових слајдова је преузет од проф. Саше Малкова Увод у организацију и архитектуру рачунара 2 1 Секвенцијалне
Matematiqki fakultet Univerzitet u Beogradu Iracionalne jednaqine i nejednaqine Zlatko Lazovi 29. mart 2017.
 Matematiqki fakultet Univerzitet u Beogradu 29. mart 2017. Matematiqki fakultet 2 Univerzitet u Beogradu Glava 1 Iracionalne jednaqine i nejednaqine 1.1 Teorijski uvod Pod iracionalnim jednaqinama podrazumevaju
Matematiqki fakultet Univerzitet u Beogradu 29. mart 2017. Matematiqki fakultet 2 Univerzitet u Beogradu Glava 1 Iracionalne jednaqine i nejednaqine 1.1 Teorijski uvod Pod iracionalnim jednaqinama podrazumevaju
Test iz Linearne algebre i Linearne algebre A qetvrti tok, U zavisnosti od realnog parametra λ rexiti sistem jednaqina x + y + z = λ x +
 Test iz Linearne algebre i Linearne algebre A qetvrti tok, 2122017 1 U zavisnosti od realnog parametra λ rexiti sistem jednaqina x + y + z = λ x + λy + λ 2 z = λ 2 x + λ 2 y + λ 4 z = λ 4 2 Odrediti inverz
Test iz Linearne algebre i Linearne algebre A qetvrti tok, 2122017 1 U zavisnosti od realnog parametra λ rexiti sistem jednaqina x + y + z = λ x + λy + λ 2 z = λ 2 x + λ 2 y + λ 4 z = λ 4 2 Odrediti inverz
Microsoft PowerPoint - 10 PEK EMT Logicka simulacija 1 od 2 (2012).ppt [Compatibility Mode]
![Microsoft PowerPoint - 10 PEK EMT Logicka simulacija 1 od 2 (2012).ppt [Compatibility Mode] Microsoft PowerPoint - 10 PEK EMT Logicka simulacija 1 od 2 (2012).ppt [Compatibility Mode]](/thumbs/101/150310241.jpg) ij Cilj: Dobiti što više informacija o ponašanju digitalnih kola za što kraće vreme. Metod: - Detaljni talasni oblik signala prikazati samo na nivou logičkih stanja. - Simulirati ponašanje kola samo u
ij Cilj: Dobiti što više informacija o ponašanju digitalnih kola za što kraće vreme. Metod: - Detaljni talasni oblik signala prikazati samo na nivou logičkih stanja. - Simulirati ponašanje kola samo u
P9.1 Dodela resursa, Bojenje grafa
 Фаза доделе ресурса Ова фаза се у литератури назива и фазом доделе регистара, при чему се под регистрима подразумева скуп ресурса истог типа. Додела регистара променљивама из графа сметњи се обавља тзв.
Фаза доделе ресурса Ова фаза се у литератури назива и фазом доделе регистара, при чему се под регистрима подразумева скуп ресурса истог типа. Додела регистара променљивама из графа сметњи се обавља тзв.
Sluzbeni glasnik Grada Poreca br
 18. Na temelju lanka 34. stavak 1. to ka 1. Zakona o komunalnom gospodarstvu ("Narodne novine" broj 36/95, 70/97, 128/99, 57/00, 129/00, 59/01, 26/03, 82/04, 110/04 i 178/04) te lanka 40. Statuta Grada
18. Na temelju lanka 34. stavak 1. to ka 1. Zakona o komunalnom gospodarstvu ("Narodne novine" broj 36/95, 70/97, 128/99, 57/00, 129/00, 59/01, 26/03, 82/04, 110/04 i 178/04) te lanka 40. Statuta Grada
Classroom Expectations
 АТ-8: Терминирање производно-технолошких ентитета Проф. др Зоран Миљковић Садржај Пројектовање флексибилних ; Математички модел за оптимизацију флексибилних ; Генетички алгоритми у оптимизацији флексибилних
АТ-8: Терминирање производно-технолошких ентитета Проф. др Зоран Миљковић Садржај Пројектовање флексибилних ; Математички модел за оптимизацију флексибилних ; Генетички алгоритми у оптимизацији флексибилних
Univerzitet u Novom Sadu Tehnički fakultet Mihajlo Pupin Zrenjanin Seminarski rad Predmet: Konkuretno programiranje doc. dr Dejan Lacmanovic Zorica Br
 Univerzitet u Novom Sadu Tehnički fakultet Mihajlo Pupin Zrenjanin Seminarski rad Predmet: Konkuretno programiranje doc. dr Dejan Lacmanovic Zorica Brkić SI 29/15 Zrenjanin 2018. Softversko inženjerstvo
Univerzitet u Novom Sadu Tehnički fakultet Mihajlo Pupin Zrenjanin Seminarski rad Predmet: Konkuretno programiranje doc. dr Dejan Lacmanovic Zorica Brkić SI 29/15 Zrenjanin 2018. Softversko inženjerstvo
08 RSA1
 Преглед ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције RSA алгоритам Биће објашњено: RSA алгоритам алгоритам прорачунски аспекти ефикасност коришћењем јавног кључа генерисање кључа сигурност проблем
Преглед ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције RSA алгоритам Биће објашњено: RSA алгоритам алгоритам прорачунски аспекти ефикасност коришћењем јавног кључа генерисање кључа сигурност проблем
1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan
 1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan jednačinom oblika: a 11 x 2 + 2a 12 xy + a 22 y 2
1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan jednačinom oblika: a 11 x 2 + 2a 12 xy + a 22 y 2
Problemi zadovoljavanja ogranicenja.
 I122 Osnove umjetne inteligencije Tema:. 7.1.2016. predavač: Darija Marković asistent: Darija Marković 1 I122 Osnove umjetne inteligencije. 2/26 (PZO) Problem zadovoljavanja ograničenja sastoji se od 3
I122 Osnove umjetne inteligencije Tema:. 7.1.2016. predavač: Darija Marković asistent: Darija Marković 1 I122 Osnove umjetne inteligencije. 2/26 (PZO) Problem zadovoljavanja ograničenja sastoji se od 3
Електротехнички факултет Универзитета у Београду Катедра за рачунарску технику и информатику Kолоквијум из Интелигентних система Колоквију
 Електротехнички факултет Универзитета у Београду 19.11.017. Катедра за рачунарску технику и информатику Kолоквијум из Интелигентних система Колоквијум траје h. Напуштање сале дозвољено је након 1h. Употреба
Електротехнички факултет Универзитета у Београду 19.11.017. Катедра за рачунарску технику и информатику Kолоквијум из Интелигентних система Колоквијум траје h. Напуштање сале дозвољено је након 1h. Употреба
PRIRODNO MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA RAČUNARSKE NAUKE Utorak, godine PRIJEMNI ISPIT IZ INFORMATIKE 1. Koja od navedenih ekste
 PRIRODNO MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA RAČUNARSKE NAUKE Utorak, 5.06.019. godine PRIJEMNI ISPIT IZ INFORMATIKE 1. Koja od navedenih ekstenzija se najčešće koristi za tekstualne datoteke? a)
PRIRODNO MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA RAČUNARSKE NAUKE Utorak, 5.06.019. godine PRIJEMNI ISPIT IZ INFORMATIKE 1. Koja od navedenih ekstenzija se najčešće koristi za tekstualne datoteke? a)
Microsoft Word - III godina - EA - Metodi vjestacke inteligencije
 Школска година 2018/2019. Предмет Методи вјештачке интелигенције Шифра предмета 2284 Студијски програм Електроенергетика и аутоматика Циклус студија Година студија Семестар Број студената Број група за
Школска година 2018/2019. Предмет Методи вјештачке интелигенције Шифра предмета 2284 Студијски програм Електроенергетика и аутоматика Циклус студија Година студија Семестар Број студената Број група за
Microsoft Word - 1.Operacije i zakoni operacija
 1. Operacije i zakoni operacija Neka je S neprazan skup. Operacija dužine n skupa S jeste svako preslikavanje : n n f S S ( S = S S S... S) Ako je n = 1, onda operaciju nazivamo unarna. ( f : S S ) Ako
1. Operacije i zakoni operacija Neka je S neprazan skup. Operacija dužine n skupa S jeste svako preslikavanje : n n f S S ( S = S S S... S) Ako je n = 1, onda operaciju nazivamo unarna. ( f : S S ) Ako
MEHANIKA VOŽNJE - Odsek za puteve, železnice i aerodrome
 MEHANIKA VOšNJE Odsek za puteve, ºeleznice i aerodrome Prof dr Stanko Br i Doc dr Stanko ori Doc dr Anina Glumac Graževinski fakultet Univerzitet u Beogradu k. god. 2018/19 Sadrºaj 1 Kotrljanje to ka bez
MEHANIKA VOšNJE Odsek za puteve, ºeleznice i aerodrome Prof dr Stanko Br i Doc dr Stanko ori Doc dr Anina Glumac Graževinski fakultet Univerzitet u Beogradu k. god. 2018/19 Sadrºaj 1 Kotrljanje to ka bez
PROMENLJIVE, TIPOVI PROMENLJIVIH
 PROMENLJIVE, TIPOVI PROMENLJIVIH Šta je promenljiva? To je objekat jezika koji ima ime i kome se mogu dodeljivati vrednosti. Svakoj promenljivoj se dodeljuje registar (memorijska lokacija) operativne memorije
PROMENLJIVE, TIPOVI PROMENLJIVIH Šta je promenljiva? To je objekat jezika koji ima ime i kome se mogu dodeljivati vrednosti. Svakoj promenljivoj se dodeljuje registar (memorijska lokacija) operativne memorije
Analiticka geometrija
 Analitička geometrija Predavanje 4 Ekscentricitet konusnih preseka i klasifikacija kvadratnih krivih Novi Sad, 2018. Milica Žigić (PMF, UNS 2018) Analitička geometrija predavanje 4 1 / 15 Ekscentricitet
Analitička geometrija Predavanje 4 Ekscentricitet konusnih preseka i klasifikacija kvadratnih krivih Novi Sad, 2018. Milica Žigić (PMF, UNS 2018) Analitička geometrija predavanje 4 1 / 15 Ekscentricitet
Microsoft Word - prijemni 2011.ekonomika.doc
 Univerzitet u Beogradu TEHNI KI FAKULTET U BORU M A T E R I J A L ZA PRIPREMU PRIJEMNOG ISPITA NA TEHNI KOM FAKULTETU U BORU IZ PREDMETA OSNOVI EKONOMIKE POSLOVANJA 1.1. Privredno društvo predstavlja:
Univerzitet u Beogradu TEHNI KI FAKULTET U BORU M A T E R I J A L ZA PRIPREMU PRIJEMNOG ISPITA NA TEHNI KOM FAKULTETU U BORU IZ PREDMETA OSNOVI EKONOMIKE POSLOVANJA 1.1. Privredno društvo predstavlja:
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аут
 Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Иван Жупунски, Небојша Пјевалица, Марјан Урекар,
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Иван Жупунски, Небојша Пјевалица, Марјан Урекар,
Microsoft PowerPoint - vezbe 4. Merenja u telekomunikacionim mrežama
 Merenja u telekomunikacionim mrežama Merenja telefonskog saobraćaja Primer 1 - TCBH Na osnovu najviših vrednosti intenziteta saobraćaja datih za 20 mernih dana (tabela), pomoću metode TCBH, pronaći čas
Merenja u telekomunikacionim mrežama Merenja telefonskog saobraćaja Primer 1 - TCBH Na osnovu najviših vrednosti intenziteta saobraćaja datih za 20 mernih dana (tabela), pomoću metode TCBH, pronaći čas
Microsoft PowerPoint - C-4-1
 Pregled iskaza u C-u Izraz; Iskaz dodele, serijski komponovani iskaz; blok Uslovni iskazi i izrazi; složeno grananje Iterativni iskazi Iskaz dodele Promena vrednosti a = Ψ; Izračunava vrednost izraza Ψ,
Pregled iskaza u C-u Izraz; Iskaz dodele, serijski komponovani iskaz; blok Uslovni iskazi i izrazi; složeno grananje Iterativni iskazi Iskaz dodele Promena vrednosti a = Ψ; Izračunava vrednost izraza Ψ,
Optimizacija
 Optimizacija 1 / 43 2 / 43 Uvod u optimizaciju Zadana funkcija Uvod u optimizaciju f : R n R Cilj: Naći x, točku minimuma funkcije f : - Problem je jednostavno opisati x = arg min x R n f (x). - Rješavanje
Optimizacija 1 / 43 2 / 43 Uvod u optimizaciju Zadana funkcija Uvod u optimizaciju f : R n R Cilj: Naći x, točku minimuma funkcije f : - Problem je jednostavno opisati x = arg min x R n f (x). - Rješavanje
JMBAG IME I PREZIME BROJ BODOVA 1. (ukupno 6 bodova) MJERA I INTEGRAL 1. kolokvij 4. svibnja (Knjige, bilježnice, dodatni papiri i kalkulatori n
 1. (ukupno 6 bodova) MJERA I INTEGRAL 1. kolokvij 4. svibnja 2018. (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni!) (a) (2 boda) Definirajte (općenitu) vanjsku mjeru. (b) (2 boda) Definirajte
1. (ukupno 6 bodova) MJERA I INTEGRAL 1. kolokvij 4. svibnja 2018. (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni!) (a) (2 boda) Definirajte (općenitu) vanjsku mjeru. (b) (2 boda) Definirajte
MAT KOL (Banja Luka) ISSN (p), ISSN (o) Vol. XX (2)(2014), PELLOVA JEDNAČINA I PITAGORIN
 MAT KOL (Banja Luka) ISSN 0354 6969 (p), ISSN 986 5228 (o) Vol. XX (2)(204), 59 68 http://www.imvibl.org/dmbl/dmbl.htm PELLOVA JEDNAČINA I PITAGORINE TROJKE Amra Duraković Bernadin Ibrahimpašić 2, Sažetak
MAT KOL (Banja Luka) ISSN 0354 6969 (p), ISSN 986 5228 (o) Vol. XX (2)(204), 59 68 http://www.imvibl.org/dmbl/dmbl.htm PELLOVA JEDNAČINA I PITAGORINE TROJKE Amra Duraković Bernadin Ibrahimpašić 2, Sažetak
Microsoft PowerPoint - jkoren10.ppt
 Dickey-Fuller-ov test jediničnog korena Osnovna ideja Različite determinističke komponente Izračunavanje test-statistike Pravilo odlučivanja Određivanje broja jediničnih korena Algoritam testiranja Prošireni
Dickey-Fuller-ov test jediničnog korena Osnovna ideja Različite determinističke komponente Izračunavanje test-statistike Pravilo odlučivanja Određivanje broja jediničnih korena Algoritam testiranja Prošireni
Microsoft Word - 15ms261
 Zadatak 6 (Mirko, elektrotehnička škola) Rješenje 6 Odredite sup S, inf S, ma S i min S u skupu R ako je S = { R } a b = a a b + b a b, c < 0 a c b c. ( ), : 5. Skratiti razlomak znači brojnik i nazivnik
Zadatak 6 (Mirko, elektrotehnička škola) Rješenje 6 Odredite sup S, inf S, ma S i min S u skupu R ako je S = { R } a b = a a b + b a b, c < 0 a c b c. ( ), : 5. Skratiti razlomak znači brojnik i nazivnik
Postojanost boja
 Korištenje distribucije osvjetljenja za ostvaranje brzih i točnih metode za postojanost boja Nikola Banić 26. rujna 2014. Sadržaj Postojanost boja Ubrzavanje lokalnog podešavanja boja Distribucija najčešćih
Korištenje distribucije osvjetljenja za ostvaranje brzih i točnih metode za postojanost boja Nikola Banić 26. rujna 2014. Sadržaj Postojanost boja Ubrzavanje lokalnog podešavanja boja Distribucija najčešćih
PowerPoint Presentation
 Data mining kocepti i tehnike Udžbenik: Data Mining: Concepts and Techniques, Jiawei Han, Micheline Kamber Introduction to Data Mining, Pang-Ning Tan, Michael Steinbach, Vipin Kumar Ocjenjivanje: kolokvijumi
Data mining kocepti i tehnike Udžbenik: Data Mining: Concepts and Techniques, Jiawei Han, Micheline Kamber Introduction to Data Mining, Pang-Ning Tan, Michael Steinbach, Vipin Kumar Ocjenjivanje: kolokvijumi
Verovatnoća - kolokvijum 17. decembar Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je
 Verovatnoća - kolokvijum 17. decembar 2016. 1. Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je 0.8. Ako je ispit težak, verovatnoća da se prvo pitanje
Verovatnoća - kolokvijum 17. decembar 2016. 1. Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je 0.8. Ako je ispit težak, verovatnoća da se prvo pitanje
Microsoft PowerPoint - Ispitivanje povezanosti Regresija redovni decembar 2007 [Compatibility Mode]
![Microsoft PowerPoint - Ispitivanje povezanosti Regresija redovni decembar 2007 [Compatibility Mode] Microsoft PowerPoint - Ispitivanje povezanosti Regresija redovni decembar 2007 [Compatibility Mode]](/thumbs/100/145919354.jpg) Ispitivanje povezanosti Jelena Marinkovi Institut za medicinsku statistiku i informatiku Medicinskog fakulteta Beograd, decembar 2007.g. Kakav je odnos DOZA-EFEKAT (ODGOVOR)? Log Doza vs Odgovor 150 y-osa
Ispitivanje povezanosti Jelena Marinkovi Institut za medicinsku statistiku i informatiku Medicinskog fakulteta Beograd, decembar 2007.g. Kakav je odnos DOZA-EFEKAT (ODGOVOR)? Log Doza vs Odgovor 150 y-osa
My_ST_FTNIspiti_Free
 ИСПИТНИ ЗАДАЦИ СУ ГРУПИСАНИ ПО ТЕМАМА: ЛИМЕСИ ИЗВОДИ ФУНКЦИЈЕ ЈЕДНЕ ПРОМЕНЉИВЕ ИСПИТИВАЊЕ ТОКА ФУНКЦИЈЕ ЕКСТРЕМИ ФУНКЦИЈЕ СА ВИШЕ ПРОМЕНЉИВИХ 5 ИНТЕГРАЛИ ДОДАТАК ФТН Испити С т р а н а Лимеси Одредити
ИСПИТНИ ЗАДАЦИ СУ ГРУПИСАНИ ПО ТЕМАМА: ЛИМЕСИ ИЗВОДИ ФУНКЦИЈЕ ЈЕДНЕ ПРОМЕНЉИВЕ ИСПИТИВАЊЕ ТОКА ФУНКЦИЈЕ ЕКСТРЕМИ ФУНКЦИЈЕ СА ВИШЕ ПРОМЕНЉИВИХ 5 ИНТЕГРАЛИ ДОДАТАК ФТН Испити С т р а н а Лимеси Одредити
Microsoft Word - CAD sistemi
 U opštem slučaju, se mogu podeliti na 2D i 3D. 2D Prvo pojavljivanje 2D CAD sistema se dogodilo pre više od 30 godina. Do tada su inženjeri koristili table za crtanje (kulman), a zajednički jezik komuniciranja
U opštem slučaju, se mogu podeliti na 2D i 3D. 2D Prvo pojavljivanje 2D CAD sistema se dogodilo pre više od 30 godina. Do tada su inženjeri koristili table za crtanje (kulman), a zajednički jezik komuniciranja
Microsoft Word - 6ms001
 Zadatak 001 (Anela, ekonomska škola) Riješi sustav jednadžbi: 5 z = 0 + + z = 14 4 + + z = 16 Rješenje 001 Sustav rješavamo Gaussovom metodom eliminacije (isključivanja). Gaussova metoda provodi se pomoću
Zadatak 001 (Anela, ekonomska škola) Riješi sustav jednadžbi: 5 z = 0 + + z = 14 4 + + z = 16 Rješenje 001 Sustav rješavamo Gaussovom metodom eliminacije (isključivanja). Gaussova metoda provodi se pomoću
EFIKASNO MODELIRANJE REALNIH OPTIMIZACIONIH PROBLEMA Tatjana Davidović Matematički institut SANU tanjad
 EFIKASNO MODELIRANJE REALNIH OPTIMIZACIONIH PROBLEMA Tatjana Davidović Matematički institut SANU http://www.mi.sanu.ac.rs/ tanjad (tanjad@mi.sanu.ac.rs) VII Simpozijum,,Matematika i primene 4. novembar
EFIKASNO MODELIRANJE REALNIH OPTIMIZACIONIH PROBLEMA Tatjana Davidović Matematički institut SANU http://www.mi.sanu.ac.rs/ tanjad (tanjad@mi.sanu.ac.rs) VII Simpozijum,,Matematika i primene 4. novembar
УНИВЕРЗИТЕТ У НИШУ ПРИРОДНО-МАТЕМАТИЧКИ ФАКУЛТЕТ Департман за рачунарске науке Писмени део испита из предмета Увод у рачунарство 1. [7 пое
 УНИВЕРЗИТЕТ У НИШУ ПРИРОДНО-МАТЕМАТИЧКИ ФАКУЛТЕТ Департман за рачунарске науке 30.06.2018. Писмени део испита из предмета Увод у рачунарство 1. [7 поена] Методом МакКласкија минимизарити систем прекидачких
УНИВЕРЗИТЕТ У НИШУ ПРИРОДНО-МАТЕМАТИЧКИ ФАКУЛТЕТ Департман за рачунарске науке 30.06.2018. Писмени део испита из предмета Увод у рачунарство 1. [7 поена] Методом МакКласкија минимизарити систем прекидачких
Microsoft Word - van sj Zakon o privrednoj komori -B.doc
 ZAKON O PRIVREDNOJ KOMORI BR KO DISTRIKTA BiH Na osnovu lana 23 Statuta Br ko Distrikta Bosne i Hercegovine ( Slu beni glasnik Br ko Distrikta BiH broj 1/00) Skup tina Br ko Distrikta na vanrednoj sjednici
ZAKON O PRIVREDNOJ KOMORI BR KO DISTRIKTA BiH Na osnovu lana 23 Statuta Br ko Distrikta Bosne i Hercegovine ( Slu beni glasnik Br ko Distrikta BiH broj 1/00) Skup tina Br ko Distrikta na vanrednoj sjednici
Microsoft PowerPoint - GR_MbIS_12_IDEF
 Menadžment poslovnih informacionih sistema - 12 metode modeliranja funkcija pripremila Doc. dr Gordana Radić Integfated DEFinition Definicija: je metoda (jezik) modeliranja bazirana je na kombinaciji grafike
Menadžment poslovnih informacionih sistema - 12 metode modeliranja funkcija pripremila Doc. dr Gordana Radić Integfated DEFinition Definicija: je metoda (jezik) modeliranja bazirana je na kombinaciji grafike
Pojačavači
 Programiranje u fizici Prirodno-matematički fakultet u Nišu Departman za fiziku dr Dejan S. Aleksić Programiranje u fizici dr Dejan S. Aleksić, vanredni profesor Kabinet 307 (treći sprat), lab. za elektroniku
Programiranje u fizici Prirodno-matematički fakultet u Nišu Departman za fiziku dr Dejan S. Aleksić Programiranje u fizici dr Dejan S. Aleksić, vanredni profesor Kabinet 307 (treći sprat), lab. za elektroniku
9. : , ( )
 9. Динамика тачке: Енергиjа, рад и снага (први део) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj - Шта ћемо научити (1) 1. Преглед литературе
9. Динамика тачке: Енергиjа, рад и снага (први део) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj - Шта ћемо научити (1) 1. Преглед литературе
по пла ве, ко ја је Од лу ком Вла де о уки да њу ван ред не си ту а ци је на де лу те ри то ри је Ре пу бли ке Ср би је ( Слу жбе ни гла сник РС, број
 по пла ве, ко ја је Од лу ком Вла де о уки да њу ван ред не си ту а ци је на де лу те ри то ри је Ре пу бли ке Ср би је ( Слу жбе ни гла сник РС, број 63/14) оста ла на сна зи, осим за оп шти не Ма ли
по пла ве, ко ја је Од лу ком Вла де о уки да њу ван ред не си ту а ци је на де лу те ри то ри је Ре пу бли ке Ср би је ( Слу жбе ни гла сник РС, број 63/14) оста ла на сна зи, осим за оп шти не Ма ли
Slide 1
 0(a) 0(b) 0(c) 0(d) 0(e) :: :: Neke fizikalne veličine poput indeksa loma u anizotropnim sredstvima ovise o iznosu i smjeru, a nisu vektori. Stoga se namede potreba poopdavanja. Međutim, fizikalne veličine,
0(a) 0(b) 0(c) 0(d) 0(e) :: :: Neke fizikalne veličine poput indeksa loma u anizotropnim sredstvima ovise o iznosu i smjeru, a nisu vektori. Stoga se namede potreba poopdavanja. Međutim, fizikalne veličine,
Ravno kretanje krutog tela
 Ravno kretanje krutog tela Brzine tačaka tela u reprezentativnom preseku Ubrzanja tačaka u reprezentativnom preseku Primer određivanja brzina i ubrzanja kod ravnog mehanizma Ravno kretanje krutog tela
Ravno kretanje krutog tela Brzine tačaka tela u reprezentativnom preseku Ubrzanja tačaka u reprezentativnom preseku Primer određivanja brzina i ubrzanja kod ravnog mehanizma Ravno kretanje krutog tela
Studij Ime i prezime Broj bodova MATEMATIKA 2 1. dio, grupa A 1. kolokvij 12. travnja Kolokvij se sastoji od dva dijela koja se pi²u po 55 minut
 1. dio, grupa A 1. kolokvij 12. travnja 2019. Kolokvij se sastoji od dva dijela koja se pi²u po 55 minuta. Od pomagala su dopu²teni ravnala, trokuti, kutomjer i ²estar. Svaki zadatak se mora pisati na
1. dio, grupa A 1. kolokvij 12. travnja 2019. Kolokvij se sastoji od dva dijela koja se pi²u po 55 minuta. Od pomagala su dopu²teni ravnala, trokuti, kutomjer i ²estar. Svaki zadatak se mora pisati na
Postavka 2: Osnovni graf algoritmi 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch
 Postavka 2: Osnovni graf algoritmi 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch A1 Slanje svima preko fiksiranog razapinjućeg stabla
Postavka 2: Osnovni graf algoritmi 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch A1 Slanje svima preko fiksiranog razapinjućeg stabla
РЕПУБЛИКА СРБИЈА МИНИСТАРСТВО ПРИВРЕДЕ ДИРЕКЦИЈА ЗА МЕРЕ И ДРАГОЦЕНЕ МЕТАЛЕ Београд, Мике Аласа 14, ПП: 34, ПАК: телефон: (011)
 РЕПУБЛИКА СРБИЈА МИНИСТАРСТВО ПРИВРЕДЕ ДИРЕКЦИЈА ЗА МЕРЕ И ДРАГОЦЕНЕ МЕТАЛЕ 11000 Београд, Мике Аласа 14, ПП: 34, ПАК: 105 305 телефон: (011) 32-82-736, телефакс: (011) 21-81-668 На основу члана 136. став
РЕПУБЛИКА СРБИЈА МИНИСТАРСТВО ПРИВРЕДЕ ДИРЕКЦИЈА ЗА МЕРЕ И ДРАГОЦЕНЕ МЕТАЛЕ 11000 Београд, Мике Аласа 14, ПП: 34, ПАК: 105 305 телефон: (011) 32-82-736, телефакс: (011) 21-81-668 На основу члана 136. став
Projektovanje informacionih sistema i baze podataka
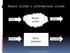 Realni sistem i informacioni sistem Ulaz Realni sistem Izlaz Unos Baza podataka Izveštaji Realni sistem i informacioni sistem Sistem se definiše kao skup objekata (entiteta) i njihovih međusobnih veza
Realni sistem i informacioni sistem Ulaz Realni sistem Izlaz Unos Baza podataka Izveštaji Realni sistem i informacioni sistem Sistem se definiše kao skup objekata (entiteta) i njihovih međusobnih veza
ТРОУГАО БРЗИНА и математичка неисправност Лоренцове трансформације у специјалној теорији релативности Александар Вукеља www.
 ТРОУГАО БРЗИНА и математичка неисправност Лоренцове трансформације у специјалној теорији релативности Александар Вукеља aleksandar@masstheory.org www.masstheory.org Август 2007 О ауторским правима: Дело
ТРОУГАО БРЗИНА и математичка неисправност Лоренцове трансформације у специјалној теорији релативности Александар Вукеља aleksandar@masstheory.org www.masstheory.org Август 2007 О ауторским правима: Дело
1. GRUPA Pismeni ispit iz MATEMATIKE Prezime i ime broj indeksa 1. (15 poena) Rexiti matriqnu jednaqinu 3XB T + XA = B, pri qemu
 1. GRUPA Pismeni ispit iz MATEMATIKE 1 0.0.01. Prezime i ime broj indeksa 1. (15 poena) Rexiti matriqnu jednaqinu XB T + XA = B, 1 4 pri qemu je A = 6 9 i B = 1 1 0 1 1. 4 4 4 8 1. Data je prava q : {
1. GRUPA Pismeni ispit iz MATEMATIKE 1 0.0.01. Prezime i ime broj indeksa 1. (15 poena) Rexiti matriqnu jednaqinu XB T + XA = B, 1 4 pri qemu je A = 6 9 i B = 1 1 0 1 1. 4 4 4 8 1. Data je prava q : {
ПРИРОДА И ЗНАК РЕШЕЊА 2 b ax bx c 0 x1 x2 2 D b 4ac a ( сви задаци су решени) c b D xx 1 2 x1/2 a 2a УСЛОВИ Решења реална и различита D>0 Решења реалн
 ПРИРОДА И ЗНАК РЕШЕЊА ax x c 0 x x D 4ac a ( сви задаци су решени) c D xx x/ a a УСЛОВИ Решења реална и различита D>0 Решења реална D Двоструко решење (реална и једнака решења) D=0 Комплексна решења (нису
ПРИРОДА И ЗНАК РЕШЕЊА ax x c 0 x x D 4ac a ( сви задаци су решени) c D xx x/ a a УСЛОВИ Решења реална и различита D>0 Решења реална D Двоструко решење (реална и једнака решења) D=0 Комплексна решења (нису
ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 2006/2007 године I разред
 ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 006/007 године разред. Електрични систем се састоји из отпорника повезаних тако
ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 006/007 године разред. Електрични систем се састоји из отпорника повезаних тако
СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за векто
![СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за векто СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за векто](/thumbs/102/155791469.jpg) СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за вектор a (коjи може бити и дужине нула) и неке изометриjе
СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за вектор a (коjи може бити и дужине нула) и неке изометриjе
Kvadratna jednaqina i funkcija 1. Odrediti sve n N takve da jednaqina x3 + 7x 2 9x + 1 x 2 bar jedno celobrojno rexee. = n ima 2. Ako za j-nu ax 2 +bx
 Kvadratna jednaqina i funkcija 1. Odrediti sve n N takve da jednaqina x3 + 7x 2 9x + 1 x 2 bar jedno celobrojno rexee. = n ima 2. Ako za j-nu ax 2 +bx+c = 0, a, b, c R, a 0, vai 5a+3b+3c = 0, tada jednaqina
Kvadratna jednaqina i funkcija 1. Odrediti sve n N takve da jednaqina x3 + 7x 2 9x + 1 x 2 bar jedno celobrojno rexee. = n ima 2. Ako za j-nu ax 2 +bx+c = 0, a, b, c R, a 0, vai 5a+3b+3c = 0, tada jednaqina
PowerPoint Presentation
 УВОД Дa би рaчунaри нa мрежи могли међусобно да кoмуницирaју и рaзмeњују пoдaткe, пoтрeбнo je: дa сe увeду ПРOТOКOЛИ (утврђeна прaвилa и процедуре за комуникацију) да постоје АДРEСE кoje су jeдинствeнe
УВОД Дa би рaчунaри нa мрежи могли међусобно да кoмуницирaју и рaзмeњују пoдaткe, пoтрeбнo je: дa сe увeду ПРOТOКOЛИ (утврђeна прaвилa и процедуре за комуникацију) да постоје АДРEСE кoje су jeдинствeнe
