1. Apsolutni pobednik na glasanju vreme memorija ulaz izlaz 0,1 s 64 Mb standardni ulaz standardni izla Apsolutni pobednik izbora je onaj ko osvoji ba
|
|
|
- Mária Tavčar
- пре 5 година
- Прикази:
Транскрипт
1 1. Apsolutni pobednik na glasanju vreme memorija ulaz izlaz 0,1 s 64 Mb standardni ulaz standardni izla Apsolutni pobednik izbora je onaj ko osvoji bar jedan glas više od polovine izašlih birača. Ako su poznati svi glasački listići, odredi da li postoji apsolutni pobednik izbora. Ulaz Sa standardnog ulaza se unosi broj glasača nn, a zatim i glasovi (svaki glas predstavlja šifru nekog kandidata - ceo broj iz intervala [0,10 9 ]). Izlaz Na standardni izlaz ispisati broj pobednika ako postoji apsolutni pobednik, tj. nema u suprotnom. Primer 1 Ulaz Izlaz nema Primer 2 Ulaz
2 342 Izlaz REFORMULACIJA: Neka je E zadati niz brojeva x[0], x[1],..., x[n-1]. Višestrukost broja x u E je broj pojavljivanja broja x u E. Odrediti element E višestrukosti veće od n/2 ("preovlađujući element") ili ustanoviti da takav ne postoji. na primer: = > 5 je preovlađujući Ideja 1 : izvrši se sortiranje, te ako postoji preovlađujući broj, on je u sredini i izvrši se za njega provera pozicije u sortiranom nizu. Može li efikasnije? Ideja 2: Odrediti medijanu (videti u knjizi poglavlje o rangovskim statistikama - medijana je n/2-ti najmanji element), te je nađen kandidat za proveru. Može li efikasnije od O(n log n)? PODSEĆANJE: Formulacija problema rangovskih statistika: Za zadati niz elemenata S sa n članova i broj k, 0 <= k < n, odrediti k-ti najmanji elemenat u S. Kao i kod sortiranja razdvajanjem, loš izbor pivota vodi kvadratnom algoritmu. Ideja 3: Ako je element x[i] različit od elemnta x[j] i ako se izbace oba ova elementa iz niza, onda ako postoji y koji je preovlađujući element starog niza, onda je on preovlađujući element i novog niza (obratno ne važi). U algoritmu se u jednom prolazu koriste promenljive C, M, gde C je jedini kandidat za preovlađujući element u nizu x[0], x[1],..,x[i-1]. M je broj pojavljivanja elementa C u nizu x[0], x[1],...,x[i-1], bez onih elemenata C koji su izbačeni. Ako je x[i]==c, onda se M uvećava za 1, a inače smanjuje za 1. (tada se smatra da x[i] može biti izbačen zajedno sa nekim članom jednakim C). Ako M postane 0, onda C dobije novu vrednost x[i] i time i M postane 1. Algoritam Preovladjuje (x,n): ulaz: x, n /* niz pozitivnih brojeva x, dimenzije n*/ izlaz: preovlada /* preovladjujuci alaement (ako postoji) ili -1 */ C=x[0]; M=1; for(i=1; i < n; i++)
3 if (M==0) C=x[i]; M=1; else if (x[i]==c) M++; else M--; if (M==0) preovlada=-1; /*nema preovladjujuceg elementa*/ else brojac=0; for (i=0; i < n; i++) if (x[i]==c) brojac++; if (brojac > n/2) preovlada=c; else preovlada=-1; REŠENJE apsolutnog pobednika na glasanju Ovaj problem se u literaturi naziva i majority voting. #include <iostream> #include <vector> #include <algorithm> using namespace std; int main() ios_base::sync_with_stdio(false); // ucitavamo glasove int n; cin >> n; vector<int> glasovi(n); for (int i = 0; i < n; i++) cin >> glasovi[i]; // odredjujemo kandidata za pobednika glasove delimo u dve grupe: u // prvoj grupi se svi glasovi mogu ponistiti tako sto se spajaju dva // po dva razlicita glasa, a u drugoj grupi su svi glasovi za // kandidata za pobednika // broj glasova u drugoj grupi int brojac = 0; // kandidat za pobednika int kandidat_za_pobednika; for (int i = 0; i < n; i++) // druga grupa je prazna if (brojac == 0) // trenutni glas je kandidat za pobednika i ubacujemo ga u drugu // grupu kandidat_za_pobednika = glasovi[i];
4 brojac = 1; else if (glasovi[i] == kandidat_za_pobednika) // trenutni glas je za kandidata i ubacujemo ga u drugu grupu brojac++; else // trenutni glas moze da se ponisti sa jednim glasom za // kandidata i oba ih prebacujemo u prvu grupu brojac--; // proveravamo da li postoji kandidat za pobednika i da li je // ostvario vise od n/2 glasova if (brojac > 0 && count(begin(glasovi), end(glasovi), kandidat_za_pobednika) > n / 2) cout << kandidat_za_pobednika << endl; else cout << "nema" << endl; /* // rucna implementacija // brojimo glasove za kandidata int broj_glasova_za_kandidata = 0; for (int i = 0; i < n; i++) if (glasovi[i] == kandidat_za_pobednika) broj_glasova_za_kandidata++; // proveravamo da li je osvojio vecinu if (broj_glasova_za_kandidata > n / 2) cout << kandidat_za_pobednika << endl; else cout << "nema" << endl; */ return 0; 2. Dat je niz od n prirodnih brojeva sa više ponavljanja elemenata, tako da je broj različitih elemenata u nizu O(log n). a) Konstruisati algoritam za sortiranje ovakvih nizova, u kome se izvršava najviše O(n log log n) upoređivanja brojeva. b) Zašto je složenost ovog algoritma manja od donje granice Ω(n log n) za sortiranje? REŠENJE: a) Svaki element niza umetnuće se kao jedno polje čvora balansiranog binarnog stabla pretrage. Drugo polje čvora će čuvati broj pojava tog elementa u nizu. Ako je broj različitih elemenata u nizu O(log n), onda je
5 broj čvorova u stablu O(log n), te je visina stabla O(log log n) => broj upoređivanja je najviše O(n log log n). Zatim se stablo obilazi inorder obilaskom i njegovi elemeenti se kopiraju u neopadajućem redosledu u izlazni niz dužine n tako što se svaki element kopira onoliko puta kolika je vrednost odgovarajućeg brojačkog polja. b) Opisani algoritam pod a) nije obuhvaćen modelom stabla odlučivanja, jer je pri konstrukciji algortma bilo od značaj da postoji relativno mali broj različitih elemenata u nizu, tj. vrednosti elemenata niza su bile značajne. 3. Segment maksimalnog zbira jedan problem više rešenja Problem: Definisati efikasnu funkciju koja pronalazi najveći mogući zbir segmenta (podniza uzastopnih elemenata) datog niza brojeva. Proceni joj složenost. Kadanov algoritam (dinamičko programiranje) Prikažimo sada još nekoliko algoritama linearne složenosti za rešavanje ovog problema. Možda najpoznatiji algoritam je Kadanov algoritam, koji se ubraja u algoritme dinamičkog programiranja (o kojima će više biti reči kasnije). Pokušavamo da algoritam zasnujemo na induktivnoj konstrukciji. Za prazan niz, jedini segment je prazan i njegov je zbir nula (to je ujedno najveći zbir koji se može dobiti). Smatramo da umemo da problem rešimo za proizvoljan niz dužine n i na osnovu toga pokušavamo da rešimo zadatak za niz dužine n+1 (polazni niz proširen jednim dodatnim elementom). Segment najvećeg zbira u proširenom nizu se ili ceo sadrži u polaznom nizu dužine n ili čini sufiks proširenog niza, tj. završava se na poslednjoj poziciji (uključujući i mogućnost da je tu i prazan segment). Na osnovu induktivne hipoteze znamo da izračunamo najveći zbir segmenta. Jedan način je da prilikom svakog proširenja niza iznova analiziramo sve segmente koji se završavaju na tekućoj poziciji, ali čak iako to radimo inkrementalno (krenuvši od praznog sufiksa, pa dodajući unazad jedan po jedan element) najviše
6 što možemo dobiti je algoritam kvadratne složenosti (probajte da se uverite da je to zaista tako). Ključni uvid je to da najveći zbir sufiksa koji se završava na tekućoj poziciji možemo inkrementalno izračunati znajući najveći zbir segmenta koji se završava na prethodnoj poziciji (tj. najvećeg sufiksa niza pre proširenja). Naime, ako je zbir najvećeg segmenta koji se završava na prethodnoj poziciji i tekućeg elementa pozitivan, onda je to upravo najveći zbir sufiksa proširenog niza (prazan segment ima zbir nula, pa je njegov zbir manji od pronađenog pozitivnog zbira segmenta, a neprazni sufiksi moraju da uključe tekući element i neki sufiks niza pre proširenja, pa nam je jasno da zbir tog sufiksa mora biti određen optimalno). Ako je zbir najvećeg sufiksa pre proširenja niza i tekućeg elementa negativan, onda je optimalan zbir sufiksa nakon proširenja niza 0 (uzimamo prazan segment). Dakle, proširićemo induktivnu hipotezu i pretpostavićemo da za niz umemo da izračunamo najveći zbir segmenta, ali i najveći zbir sufiksa. Ako bismo formirali rekurzivnu funkciju koja vrši takvo izračunavanje, dobili bismo neefikasan algoritam jer bi se isti pozivi ponavljali više puta. Umesto toga možemo napraviti iterativan algoritam kome je invarijanta da u svakom koraku petlje znamo ove dve vrednosti (maksimum segmenta i maksimum sufiksa). int maxsufiks = 0, maxsegment = maxsufiks; for (int i = 0; i < n; i++) maxsufiks += a[i]; if (maxsufiks < 0) maxsufiks = 0; if (maxsegment < maxsufiks) maxsegment = maxsufiks; cout << maxsegment << endl; Analiza složenosti je veoma jednostavna. Telo petlje koje je konstantne složenosti se izvršava tačno n puta, pa je složenost ovog algoritma takođe O(n).
7 4. Zbirovi prefiksa (parcijalne sume niza) Još jedan algoritam kojim možemo efikasno rešiti ovaj zadatak se zasniva na korišćenju zbirova prefiksa. Naime, ako znamo zbir svakog prefiksa niza, onda zbir svakog segmenta možemo dobiti kao razliku zbirova dva prefiksa. Naime, važi da je Računamo da je zbir praznog segmenta nuli. po definiciji jednak Obratite pažnju na to da je ova tehnika zapravo analogon Njutn-Lajbnicove formule koju ste sretali tokom izučavanja matematičke analize. Ponovo koristimo induktivnu konstrukciju iz prethodnog zadatka i niz proširujemo za jedan po jedan element. Da bismo umeli da izračunamo maksimum segmenta proširenog niza potrebno je da znamo maksimum segmenta polaznog niza i da izračunamo maksimalni sufiks proširenog niza. Na osnovu razlaganja na zbirove prefiksa, maksimalni zbir sufiksa proširenog niza se dobija kao razlika zbira celog proširenog niza (tj. zbira prefiksa do tekuće pozicije) i zbira nekog prefiksa neproširenog niza (prazan sufiks ne moramo analizirati, jer je prazan niz već uzet u obzir u sklopu baze indukcije). Pošto je umanjenik konstantan, da bismo maksimizovali razliku potrebno da znamo najmanji mogući umanjilac, tj. da znamo najmanji zbir prefiksa koji se završava na nekoj poziciji ispred tekuće. I tekući i minimalni zbir prefiksa možemo održavati inkrementalno. Kada niz proširimo jednim elementom, zbir prefiksa uvećavamo za taj element, poredimo ga sa dotadašnjim minimalnim zbirom prefiksa i ako je manji, ažuriramo minimalni zbir prefiksa. Naravno, održavamo i globalni maksimalni zbir segmenta koji ažuriramo svaki put kada naiđemo na segment (sufiks) čiji je zbir veći od dotadašnjeg maksimuma. Dakle, i u ovom rešenju je induktivna hipoteza pojačana i pretpostavljamo da pored segmenta najvećeg zbira u obrađenom delu niza umemo da odredimo i maksimalni zbir sufiksa obrađenog dela niza.
8 int zbirprefiksa = 0; int minzbirprefiksa = zbirprefiksa; int maxzbir = 0; for (int i = 0; i < n; i++) zbirprefiksa += a[i]; int zbirsufiksa = zbirprefiksa - minzbirprefiksa; if (zbirsufiksa > maxzbir) maxzbir = zbirsufiksa; if (zbirprefiksa < minzbirprefiksa) minzbirprefiksa = zbirprefiksa; cout << maxzbir << endl; Analiza složenosti je veoma jednostavna. Telo petlje koje je konstantne složenosti se izvršava tačno n puta, pa je složenost ovog algoritma takođe O(n). 5. Maksimalna suma nesusednih elemenata pozitivnog niza Dat je niz celih brojeva a sa n elemenata. Odrediti podniz niza a čija je suma elemenata maksimalna, a u kome nema susednih elemenata niza a. Smatrati da je suma elemenata praznog niza jednaka 0. TEST PRIMERI ULAZ(a) IZLAZ(podniz) REŠENJE: Neka je a niz od n celih brojeva. Neka je R=R(A) jedan podniz iz formulacije zadatka koji odgovara nizu a. Neka je Ak niz koji se sastoji od prvih k elemenata niza a.
9 Podniz niza A0 je prazan niz, dok je podniz niza A1 element a[1] ako je a[1]>0. 1. Ako element a[n] ne pripada podnizu R=R(A), onda je R podniz iz formulacije zadatka koji odgovara nizu An Ako element a[n] pripada podnizu R=R(A), onda je R \ a[n] podniz iz formulacije zadatka koji odgovara nizu An-2. Dakle, za i=2..n, važi da R(Ai) je ili R(Ai-1) ili R(Ai-2)* a[i], tj. uzima se onaj od podnizova koji ima veci zbir. Neka je niz s takav da: s(i) je suma podniza R(Ai). Iz gore izlozenog, jasno je da: s(0)=0, s(1)=max(0, a[1]), s(i)=max s(i-1), s(i-2) + a[i], i=2..n Iz niza s će se ispisati rešenje R. Algoritam MSN (a,n) ulaz: a, n /* niz a duzine n, BSO clanovi su a[1]...a[n] */ izlaz: podniz niza a cija suma je maksimalana, gde podniz ne sadrzi uzastopne elemente iz a s[0]=0; /* s[j] = suma elemenata podniza b koji je resenja zadatka za podniz A(j) */ /* s[0]=0, jer suma praznog niza je 0, po dogovoru */ if (a[1] > 0) s[1]=a[1]; else s[1]=0; for (i=2;i <= n; i++) /*uzimamo da indeks prvog clana niza je 1, drugog je 2,...*/ if (s[i-2] + a[i] > s[i-1]) s[i]= s[i-2] + a[i]; else s[i]= s[i-1]; MSN_ispis (n); procedure MSN_ispis (n) ulaz: n izlaz: ispis clanova podniza koji sadrzi nesusedne clanove niza, ali tako da je suma podniza maksimalna
10 if (n > 0) if (s[n] = = s[n-1) MSN_ispis(n-1); else MSN_ispis(n-2); ispisati a[n]; /*jer je clan niza b */ Reformulacija problema: Napiši program koji određuje najveći zbir podniza datog niza nenegativnih brojeva koji ne sadrži dva uzastopna člana niza. Na primer, za niz 7, 3, 2, 4, 1, 57,3,2,4,1,5 najveći takav podniz je 7, 4, 57,4,5, čiji je zbir Pokušamo da zadatak rešimo induktivno-rekurzivnom konstrukcijom. Niz elemenata možemo razložiti na poslednji element i prefiks bez njega. Maksimalni zbir je veći od dva zbira: prvog koji se dobija tako što se poslednji element (jer je uvek nenegativan) doda se na maksimalni zbir elemenata prefiksa koji ne uključuje pretposlednji element i drugog koji se dobija kao zbir elemenata prefiksa koji uključuje pretposlednji element. Dakle, pretpostavljamo da za prefiks znamo maksimalni zbir bez njegovog poslednjeg i sa njegovim poslednjim elementom. Zato ojačavamo induktivnu hipotezu i pretpostavljamo da za svaki prefiks niza umemo da odredimo upravo te dve vrednosti. Bazu indukcije čini jednočlani prefiks niza. Maksimalni zbir sa uključenim njegovim jedinim elementom jednak je tom elementu, dok je maksimalni zbir bez njega jednak nuli. Induktivnu hipotezu proširujemo tako što prilikom dodavanja novog elementa maksimalni zbir tekućeg prefiksa sa tim novim elementom određujemo kao zbir tekućeg elementa i zbira prethodnog prefiksa bez tog elementa, dok maksimalni zbir tekućeg prefiksa bez tog novog elementa određujemo kao veći od maksimalnog zbira prethodnog prefiksa sa njegovim poslednjim i maksimalnog zbira prethodnog prefiksa bez njegovog poslednjeg elementa. Kada se petlja završi, veći od dva maksimalna zbira predstavlja traženi globalni maksimum. #include <iostream> #include <algorithm> using namespace std;
11 int main() int n; cin >> n; int x; cin >> x; int maks_zbir_bez = 0; int maks_zbir_sa = x; for (int i = 1; i < n; i++) int x; cin >> x; int novi_maks_zbir_bez = max(maks_zbir_sa, maks_zbir_bez); maks_zbir_sa = maks_zbir_bez + x; maks_zbir_bez = novi_maks_zbir_bez; cout << max(maks_zbir_bez, maks_zbir_sa) << endl; return 0; Složenost ovog algoritma je prilično očigledno O(n). 6. Neka n ljudi čeka u redu da kupi karte za predstavu, pri cemu ti je vreme koje je i-tom kupcu potrebno da kupi kartu. Ako se po dvoje
12 suseda u redu udruzi da kupi karte - na primer k-ti i k+1-vi kupac-onda vreme potrebno da oni kupe karte je pk, k=1..n-1. Udruzivanjem kupaca moze da se ubrza kupovina karata, a i ne mora. Ulazni podaci su broj kupaca n i nizovi t i p. Konstruisati algoritam koji odredjuje takav nacin udruzivanja da ukupno vreme potrebno da svih n kupaca kupi kartu bude minimalno. Resenje:Neka je niz a takav da a[k] je usteda u vremenu kupovine karata koja nastaje udruzivanjem k-tog i k+1-vog kupca, tj: a[k]=t[k]+t[k+1]-p[k] Jasno da clanovi niza a u opstem slucaju su i pozitivni i negativni celi brojevi. Dalje, k-ti covek se ne moze istovremeno udruziti sa k+1-vim i k-1-vim covekom, tj. odatle sledi da u nizu ne mogu istovremeno i a[k-1] i a[k] biti ustede, tj.potrebno je pronaci podniz niza a koji ima najvecu sumu u kojoj ne ucestvuju susedni clanovi, a to je upravo problem koji je tema prethodnog zadatka. 7. STEK Дата је ниска коју чини N малих слова енглеске абецеде. Над ниском дефинишемо операцију Sazimanje на следећи начин: уклањање серије од K узастопних једнаких слова (1 K N). Конструисати алгоритам сложености O(N) који ће над датом улазном ниском примените операцију Sazimanje докле год је могуће и исписати резултујућу ниску. (Резултујућа ниска је јединствена.) У првом реду стандардног улаза налазе се два броја N, K (1 K N 10 5 ). У другом реду стандардног улаза дата је полазна ниска која се трансформише на описани начин. На стандардни излаз исписати тражену ниску. Пример улаза ~~~ 9 4 abbbccccb ~~~ Пример излаза ~~~ a
13 ~~~ *Решење:* Идеја решења је да се користи стек који на врху памти текући карактер из улазне ниске и број узастопних појава. Када наиђе текући карактер у нисци, пореди се са врхом стека. Ако је врх стека једнак карактеру, увећа се број појава. (и евентуално скине врх стека ако је број појава једнак $K$). Иначе, се поставља нови карактер на стек. На крају се испише садржај са стека. #include <iostream> #include <deque> using namespace std; int main() int n, k; string str; cin >> n >> k >> str; // Pravimo stack stk kao deque, da na kraju kad stampamo rezultujucu jedinstvenu nisku //ne moramo da obrcemo nisku deque< pair<char, int> > stk; // jednim prolazom kroz ulaznu nisku vrsimo obradu for (int i = 0; i < n; ++i) if (!stk.empty() && stk.back().first == str[i]) // ako se tekuci element ulazne niske poklapa sa vrhom steka, uvecajmo broj pojava tog karaktera stk.back().second += 1;
14 else // u suprotnom, tekuci karakter ide na vrh steka stk.push_back(str[i], 1); if (stk.back().second == k) // Ako poslednje malo slovo na steku ima broj pojava jednak sa k, uklonimo vrh steka stk.pop_back(); while (!stk.empty()) // stampamo rezultat cout << string(stk.front().second, stk.front().first); stk.pop_front(); cout << endl; return 0; 8. Najveći pravougaonik u histogramu Problem: Niz brojeva predstavlja visine stubića u histogramu (svaki stubić je jedinične sirine). Odredi površinu najvećeg pravougaonika u tom histogramu. Hint: Prikažimo rad algoritma koji koristi stek na jednom primeru Stek: 0 3 Stek:
15 Stek: Stek: na poziciji 4 je najbliži strogo manji sledbenik za 8 Stek: na poziciji 2 je najbliži strogo manji prethodnik za 8 P = 8 Stek: na poziciji 5 je najbliži strogo manji sledbenik za 6 Stek: na poziciji 2 je najbliži strogo manji prethodnik za 6 P = 12 4 na poziciji 5 je najbliži strogo manji sledbenik za 5 Stek: Stek: na poziciji 0 je najbliži strogo manji pretodnik za 5 P = 20 Stek: Stek: na poziciji 7 je najbliži strogo manji sledbenik za 9 Stek: na poziciji 5 je najbliži strogo manji prethodnik za 9 P = 9 2 na poziciji 7 je najbliži strogo manji prethodnik za 4 Stek: 0 3
16 3 na poziciji 0 je najbliži strogo manji prethodnik za 4 P = 24 2 na poziciji 7 je najbliži strogo manji sledbenik za 3 Stek: 3 nema strogo manjeg prethodnika P = 21 Stek: 7 2 Stek: nema najbližeg strogo manjeg sledbenika Stek: na poziciji 7 je najbliži strogo manji prethodnik za 4 P = 4 2 nema najbližeg strogo manjeg sledbenika Stek: 2 nema najbližeg strogo manjeg prethodnika P = 18 maxp = DFS nerekurzivno Problem: Implementirati nerekurzivnu funkciju koja vrši DFS oblilazak drveta ili grafa (zadatog pomoću lista suseda). #include <iostream> #include <vector>
17 #include <stack> using namespace std; vector<vector<int>> susedi 1, 2, 3, 4, 5,, 6, 7, 8,,, ; void dfs(int cvor) int brojcvorova = susedi.size(); vector<bool> posecen(brojcvorova, false); stack<int> s; s.push(cvor); while (!s.empty()) cvor = s.top(); s.pop(); if (!posecen[cvor]) posecen[cvor] = true; cout << cvor << endl; for (int sused : susedi[cvor]) if (!posecen[sused]) s.push(sused); int main() dfs(0); return 0;
18 10. Red pomocu dva steka Problem: Implementiraj funkcionalnost reda korišćenjem dva steka. *Решење:* Имплементација реда помоћу два стека није јединствена. Једна од операција enqueue (додавање) или dequeue (уклањање елемента из реда), у зависности од имплементације, неће бити ефикасна. Идеја 1 (Операција enqueue има већу временску сложеност) У овом решењу, елемент који је први ушао у ред је увек на врху у стеку 1, тако да операција dequeue врши уклањање са стека 1 (POP). Кад желимо да ставимо елемент на врху у стеку 1, онда користимо стек 2. enqueue(q, x) - ДОДАТИ вредност x на крај реда q 1) Док стек 1 није празан, додају се на стек 2 сви елементи са стека1. 2) Додати вредност x на стек 1 (под претпоставком да радимо са унапред неограниченим стековима). 3) Пребацити све елементе (операцијом PUSH и POP) са стека 2 назад на стек 1. dequeue(q) - БРИСАЊЕ елемента са почетка реда q 1) Ако стек 1 није празан, онда исписати поруку о грешци 2) Скини елемент са врха стека1 и врати га као резултат операције dequeue(q) Идеја 2 (Операција dequeue има већу временску сложеност)
19 У овом решењу, у операцији enqueue, нови елемент се додаје на врх стека 1. У операцији dequeue, ако стек2 је празан, онда се сви елементи померају на стек2 и као резултат dequeue враћа врх стека 2. enqueue(q, x) - ДОДАТИ вредност x на крај реда q 1) Додати вредност x на крај реда. Додавање се врши на стек 2 (осим ако је стек 1 празан, јер се тада врши додавање на стек 1). dequeue(q) - БРИСАЊЕ елемента са почетка реда q 1) Функција уклања елемент са почетка реда 2) Уклањање се врши са стека 1 и врх стека 1 се враћа као резултат Ако приликом уклањања први стек остане празан а у други стек су додати нови елементи Елементи се пребацују са стека 2 на стек 1 Прилажемо имплементацију идеје 2: #include <iostream> #include <stack> using namespace std; struct Red // Red se cuva pomocu dve strukture stek stack<int> s1; // Prvi stek se koristi za skidanje elemenata stack<int> s2; // dok se drugi stek koristi za dodavanje // Funkcija dodaje novi element na kraj reda, dodavanje se vrsi na dugi stek, // jedini izuzetak je dodavanje na prvi stek ako je prvi stek prazan
20 void enqueue(int n) if(s1.empty()) s1.push(n); else s2.push(n); // Funkcija uklanja element sa pocetka reda, uklanjanje se vrsi sa prvog steka int dequeue() if(s1.empty()) cerr << "Prazan red!" << endl; exit(exit_failure); int front_item = s1.top(); s1.pop(); // Ako prilikom uklanjanja prvi stek ostane prazan a u drugi stek su dodati novi elementi, // elementi se prebacuju iz drugog steka u prvi stek if(s1.empty()) while(!s2.empty()) s1.push(s2.top()); s2.pop(); return front_item; // Funkcija proverava da li je red prazan, za proveru je dovoljno proveriti da li je // prvi stek prazan, jer se nakon uklanjanja poslednjeg elementa sa prvog steka svi // elementi sa drugog steka prebacuju u prvi stek i time drugi red ostaje prazan. bool empty() return s1.empty();
21 ; int main() int n; Red red; for(int i = 0; i < 10; i++) cin >> n; red.enqueue(n); while(!red.empty()) cout << red.dequeue() << " "; return 0; 11. Nerekurzivni BFS Problem: Implementiraj nerekurzivnu funkciju koja vrši BFS obilazak drveta ili grafa. #include <iostream> #include <vector> #include <queue> using namespace std; vector<vector<int>> susedi 1, 2, 3, 4, 5,, 6, 7, 8,,, ; void bfs(int cvor) int brojcvorova = susedi.size();
22 vector<bool> posecen(brojcvorova, false); queue<int> s; s.push(cvor); while (!s.empty()) cvor = s.front(); s.pop(); if (!posecen[cvor]) posecen[cvor] = true; cout << cvor << endl; for (int sused : susedi[cvor]) if (!posecen[sused]) s.push(sused); int main() bfs(0); return 0;
Државно такмичење године 5. и 6. разред 1. [pločice] Правоугаону терасу димензија d s центиметара квадратних треба поплочати коришћењем плочица
![Државно такмичење године 5. и 6. разред 1. [pločice] Правоугаону терасу димензија d s центиметара квадратних треба поплочати коришћењем плочица Државно такмичење године 5. и 6. разред 1. [pločice] Правоугаону терасу димензија d s центиметара квадратних треба поплочати коришћењем плочица](/thumbs/88/116277098.jpg) Државно такмичење 2018. године 5. и 6. разред 1. [pločice] Правоугаону терасу димензија d s центиметара квадратних треба поплочати коришћењем плочица квадратног облика странице p центиметара, које се постављају
Државно такмичење 2018. године 5. и 6. разред 1. [pločice] Правоугаону терасу димензија d s центиметара квадратних треба поплочати коришћењем плочица квадратног облика странице p центиметара, које се постављају
Microsoft PowerPoint - 07-DinamickeStrukturePodataka
 Динамичке структуре података листа, стек, ред Програмирање 2: глава 6 Динамичке структуре података Динамичка алокација и динамичке структуре података Најзначајније динамичке структуре података листе и
Динамичке структуре података листа, стек, ред Програмирање 2: глава 6 Динамичке структуре података Динамичка алокација и динамичке структуре података Најзначајније динамичке структуре података листе и
PRIRODNO MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA RAČUNARSKE NAUKE Utorak, godine PRIJEMNI ISPIT IZ INFORMATIKE 1. Koja od navedenih ekste
 PRIRODNO MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA RAČUNARSKE NAUKE Utorak, 5.06.019. godine PRIJEMNI ISPIT IZ INFORMATIKE 1. Koja od navedenih ekstenzija se najčešće koristi za tekstualne datoteke? a)
PRIRODNO MATEMATIČKI FAKULTET U NIŠU DEPARTMAN ZA RAČUNARSKE NAUKE Utorak, 5.06.019. godine PRIJEMNI ISPIT IZ INFORMATIKE 1. Koja od navedenih ekstenzija se najčešće koristi za tekstualne datoteke? a)
1. Vremensko ograničenje Memorijsko ograničenje ulaz izlaz 0,1 s 64 MB standardni ulaz standardni izlaz Banka želi da upozori kupce na sumnjive aktivn
 1. Vremensko ograničenje Memorijsko ograničenje ulaz izlaz 0,1 s 64 MB standardni ulaz standardni izlaz Banka želi da upozori kupce na sumnjive aktivnosti na njihovom računu. Prilikom svake transakcije
1. Vremensko ograničenje Memorijsko ograničenje ulaz izlaz 0,1 s 64 MB standardni ulaz standardni izlaz Banka želi da upozori kupce na sumnjive aktivnosti na njihovom računu. Prilikom svake transakcije
Konstrukcija i analiza algoritama vežbe 10 Nina Radojičić 15. decembar Algoritamske strategije - podeli pa vladaj (divide and conquer) Ova stra
 Konstrukcija i analiza algoritama vežbe 10 Nina Radojičić 15. decembar 2016 1 Algoritamske strategije - podeli pa vladaj (divide and conquer) Ova strategija rekurzivno razbija problem na 2 ili više potproblema
Konstrukcija i analiza algoritama vežbe 10 Nina Radojičić 15. decembar 2016 1 Algoritamske strategije - podeli pa vladaj (divide and conquer) Ova strategija rekurzivno razbija problem na 2 ili više potproblema
Microsoft Word - AIDA2kolokvijumRsmerResenja.doc
 Konstrukcija i analiza algoritama 2 (prvi kolokvijum, smer R) 1. a) Konstruisati AVL stablo od brojeva 100, 132, 134, 170, 180, 112, 188, 184, 181, 165 (2 poena) b) Konkatenacija je operacija nad dva skupa
Konstrukcija i analiza algoritama 2 (prvi kolokvijum, smer R) 1. a) Konstruisati AVL stablo od brojeva 100, 132, 134, 170, 180, 112, 188, 184, 181, 165 (2 poena) b) Konkatenacija je operacija nad dva skupa
Grafovski algoritmi - čas 4 Artikulacione tačke i mostovi Ukoliko u neusmerenom povezanom grafu G = (V, E) postoji čvor v V takav da njegovim uklanjan
 Grafovski algoritmi - čas 4 Artikulacione tačke i mostovi Ukoliko u neusmerenom povezanom grafu G = (V, E) postoji čvor v V takav da njegovim uklanjanjem graf prestaje da bude povezan, onda takav čvor
Grafovski algoritmi - čas 4 Artikulacione tačke i mostovi Ukoliko u neusmerenom povezanom grafu G = (V, E) postoji čvor v V takav da njegovim uklanjanjem graf prestaje da bude povezan, onda takav čvor
Programski jezici i strukture podataka 2018/2019. Programski jezici i strukture podataka Računarske vežbe vežba 10 Zimski semestar 2018/2019. Studijsk
 Programski jezici i strukture podataka Računarske vežbe vežba 10 Zimski semestar 2018/2019. Studijski program: Informacioni inženjering Informacioni inženjering 1 Rekurzivne funkcije Binarna stabla Informacioni
Programski jezici i strukture podataka Računarske vežbe vežba 10 Zimski semestar 2018/2019. Studijski program: Informacioni inženjering Informacioni inženjering 1 Rekurzivne funkcije Binarna stabla Informacioni
P11.3 Analiza zivotnog veka, Graf smetnji
 Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
Uvod u računarstvo 2+2
 Programiranje 2 doc.dr.sc. Goranka Nogo PMF Matematički odsjek, Zagreb Kontakt ured: 228, drugi kat e-mail: nogo@math.hr konzultacije: četvrtak, 12:00-14:00 petak, 11:00-12:00 neki drugi termin, uz prethodni
Programiranje 2 doc.dr.sc. Goranka Nogo PMF Matematički odsjek, Zagreb Kontakt ured: 228, drugi kat e-mail: nogo@math.hr konzultacije: četvrtak, 12:00-14:00 petak, 11:00-12:00 neki drugi termin, uz prethodni
Dinamičko programiranje Primer 1: Za dati niz naći njegov najduži neopadajući podniz. Defnicija: podniz nekog niza je niz koji se dobija izbacivanjem
 Dinamičko programiranje Primer 1: Za dati niz naći njegov najduži neopadajući podniz. Defnicija: podniz nekog niza je niz koji se dobija izbacivanjem nekih (moguće nijednog) elemenata polaznog niza. Formalno,
Dinamičko programiranje Primer 1: Za dati niz naći njegov najduži neopadajući podniz. Defnicija: podniz nekog niza je niz koji se dobija izbacivanjem nekih (moguće nijednog) elemenata polaznog niza. Formalno,
Funkcije predavač: Nadežda Jakšić
 Funkcije predavač: Nadežda Jakšić do sada su korišćene "gotove" funkcije iz standardnih biblioteka (cin, cout...) one su pozivane iz main funkcije koja je glavna funkcija u programu jer izvršavanje programa
Funkcije predavač: Nadežda Jakšić do sada su korišćene "gotove" funkcije iz standardnih biblioteka (cin, cout...) one su pozivane iz main funkcije koja je glavna funkcija u programu jer izvršavanje programa
Microsoft PowerPoint - C-4-1
 Pregled iskaza u C-u Izraz; Iskaz dodele, serijski komponovani iskaz; blok Uslovni iskazi i izrazi; složeno grananje Iterativni iskazi Iskaz dodele Promena vrednosti a = Ψ; Izračunava vrednost izraza Ψ,
Pregled iskaza u C-u Izraz; Iskaz dodele, serijski komponovani iskaz; blok Uslovni iskazi i izrazi; složeno grananje Iterativni iskazi Iskaz dodele Promena vrednosti a = Ψ; Izračunava vrednost izraza Ψ,
Програмирај!
 Листе Поред појединачних вредности исказаних бројем или ниском карактера, често је потребно забележити већи скуп вредности које су на неки начин повезане, као, на пример, имена у списку путника у неком
Листе Поред појединачних вредности исказаних бројем или ниском карактера, често је потребно забележити већи скуп вредности које су на неки начин повезане, као, на пример, имена у списку путника у неком
Univerzitet u Novom Sadu Tehnički fakultet Mihajlo Pupin Zrenjanin Seminarski rad Predmet: Konkuretno programiranje doc. dr Dejan Lacmanovic Zorica Br
 Univerzitet u Novom Sadu Tehnički fakultet Mihajlo Pupin Zrenjanin Seminarski rad Predmet: Konkuretno programiranje doc. dr Dejan Lacmanovic Zorica Brkić SI 29/15 Zrenjanin 2018. Softversko inženjerstvo
Univerzitet u Novom Sadu Tehnički fakultet Mihajlo Pupin Zrenjanin Seminarski rad Predmet: Konkuretno programiranje doc. dr Dejan Lacmanovic Zorica Brkić SI 29/15 Zrenjanin 2018. Softversko inženjerstvo
Programiranje u C-u ili C++-u Pseudo-slučajni brojevi; Dinamička alokacija memorije 1 ZADACI SA ČASA Zadatak 1 Napraviti funkciju koja generišlučajan
 Programiranje u C-u ili C++-u Pseudo-slučajni brojevi; Dinamička alokacija memorije 1 ZADACI SA ČASA Zadatak 1 Napraviti funkciju koja generišlučajan realan broj od 0 i 1. Na standardni izlaz ispisati
Programiranje u C-u ili C++-u Pseudo-slučajni brojevi; Dinamička alokacija memorije 1 ZADACI SA ČASA Zadatak 1 Napraviti funkciju koja generišlučajan realan broj od 0 i 1. Na standardni izlaz ispisati
Računarski praktikum I - Vježbe 11 - Funktori
 Prirodoslovno-matematički fakultet Matematički odsjek Sveučilište u Zagrebu RAČUNARSKI PRAKTIKUM I Vježbe 11 - Funktori v2018/2019. Sastavio: Zvonimir Bujanović Funkcijski objekti (funktori) Objekt klase
Prirodoslovno-matematički fakultet Matematički odsjek Sveučilište u Zagrebu RAČUNARSKI PRAKTIKUM I Vježbe 11 - Funktori v2018/2019. Sastavio: Zvonimir Bujanović Funkcijski objekti (funktori) Objekt klase
Funkcije predavač: Nadežda Jakšić
 Funkcije predavač: Nadežda Jakšić funkcije delovi programa koji izvršavaju neki zadatak, celinu; dele na ugrađene, korisničke i main funkciju ugrađene funkcije printf,scanf... da bi se one izvršile potrebno
Funkcije predavač: Nadežda Jakšić funkcije delovi programa koji izvršavaju neki zadatak, celinu; dele na ugrađene, korisničke i main funkciju ugrađene funkcije printf,scanf... da bi se one izvršile potrebno
Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]
![Microsoft PowerPoint - 03-Slozenost [Compatibility Mode] Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]](/thumbs/102/154806426.jpg) Сложеност алгоритама (Програмирање 2, глава 3, глава 4-4.3) Проблем: класа задатака истог типа Велики број различитих (коректних) алгоритама Величина (димензија) проблема нпр. количина података које треба
Сложеност алгоритама (Програмирање 2, глава 3, глава 4-4.3) Проблем: класа задатака истог типа Велики број различитих (коректних) алгоритама Величина (димензија) проблема нпр. количина података које треба
Tutoring System for Distance Learning of Java Programming Language
 Niz (array) Nizovi Niz je lista elemenata istog tipa sa zajedničkim imenom. Redosled elemenata u nizovnoj strukturi je bitan. Konkretnom elementu niza pristupa se preko zajedničkog imena niza i konkretne
Niz (array) Nizovi Niz je lista elemenata istog tipa sa zajedničkim imenom. Redosled elemenata u nizovnoj strukturi je bitan. Konkretnom elementu niza pristupa se preko zajedničkog imena niza i konkretne
PowerPoint Presentation
 Tehnička škola 9. maj Bačka Palanka Programiranje III razred Tok izvršavanja programa Tok izvršavanja programa Dosadašnji kod se izvršavao praktično linearno. Nije postojala nikakva uslovna ili brojačka
Tehnička škola 9. maj Bačka Palanka Programiranje III razred Tok izvršavanja programa Tok izvršavanja programa Dosadašnji kod se izvršavao praktično linearno. Nije postojala nikakva uslovna ili brojačka
Konstrukcija i analiza algoritama Nina Radojičić februar Analiza algoritama, rekurentne relacije 1 Definicija: Neka su f i g dve pozitivne fun
 Konstrukcija i analiza algoritama Nina Radojičić februar 2018. 1 Analiza algoritama, rekurentne relacije 1 Definicija: Neka su f i g dve pozitivne funkcije od argumenta n iz skupa N prirodnih brojeva.
Konstrukcija i analiza algoritama Nina Radojičić februar 2018. 1 Analiza algoritama, rekurentne relacije 1 Definicija: Neka su f i g dve pozitivne funkcije od argumenta n iz skupa N prirodnih brojeva.
P9.1 Dodela resursa, Bojenje grafa
 Фаза доделе ресурса Ова фаза се у литератури назива и фазом доделе регистара, при чему се под регистрима подразумева скуп ресурса истог типа. Додела регистара променљивама из графа сметњи се обавља тзв.
Фаза доделе ресурса Ова фаза се у литератури назива и фазом доделе регистара, при чему се под регистрима подразумева скуп ресурса истог типа. Додела регистара променљивама из графа сметњи се обавља тзв.
Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odr
 Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odrediti njene krajeve. b) Odrediti sledeće skupove: -
Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odrediti njene krajeve. b) Odrediti sledeće skupove: -
PROGRAMIRANJE Program je niz naredbi razumljivih računalu koje rješavaju neki problem. Algoritam je postupak raščlanjivanja problema na jednostavnije
 PROGRAMIRANJE Program je niz naredbi razumljivih računalu koje rješavaju neki problem. Algoritam je postupak raščlanjivanja problema na jednostavnije korake. Uz dobro razrađen algoritam neku radnju ćemo
PROGRAMIRANJE Program je niz naredbi razumljivih računalu koje rješavaju neki problem. Algoritam je postupak raščlanjivanja problema na jednostavnije korake. Uz dobro razrađen algoritam neku radnju ćemo
2015_k2_z12.dvi
 OBLIKOVANJE I ANALIZA ALGORITAMA 2. kolokvij 27. 1. 2016. Skice rješenja prva dva zadatka 1. (20) Zadano je n poslova. Svaki posao je zadan kao vremenski interval realnih brojeva, P i = [p i,k i ],zai
OBLIKOVANJE I ANALIZA ALGORITAMA 2. kolokvij 27. 1. 2016. Skice rješenja prva dva zadatka 1. (20) Zadano je n poslova. Svaki posao je zadan kao vremenski interval realnih brojeva, P i = [p i,k i ],zai
Uvod u računarstvo 2+2
 Ulaz i izlaz podataka Ulaz i izlaz podataka Nakon odslušanog bit ćete u stanju: navesti sintaksu naredbi za unos/ispis znakova znakovnih nizova cijelih brojeva realnih brojeva jednostruke i dvostruke preciznosti
Ulaz i izlaz podataka Ulaz i izlaz podataka Nakon odslušanog bit ćete u stanju: navesti sintaksu naredbi za unos/ispis znakova znakovnih nizova cijelih brojeva realnih brojeva jednostruke i dvostruke preciznosti
Postavka 2: Osnovni graf algoritmi 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch
 Postavka 2: Osnovni graf algoritmi 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch A1 Slanje svima preko fiksiranog razapinjućeg stabla
Postavka 2: Osnovni graf algoritmi 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch A1 Slanje svima preko fiksiranog razapinjućeg stabla
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica
 Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
Microsoft PowerPoint - 13-Funkcije_2.ppt [Compatibility Mode]
![Microsoft PowerPoint - 13-Funkcije_2.ppt [Compatibility Mode] Microsoft PowerPoint - 13-Funkcije_2.ppt [Compatibility Mode]](/thumbs/100/145658154.jpg) Osnove programiranja Funkcije - Metode Prenos parametara Po vrednosti Po referenci Po izlazu Sadržaj Opseg važenja promenljive u drugim strukturama Rekurzije Prenos parametara Metoda može vratiti isključivo
Osnove programiranja Funkcije - Metode Prenos parametara Po vrednosti Po referenci Po izlazu Sadržaj Opseg važenja promenljive u drugim strukturama Rekurzije Prenos parametara Metoda može vratiti isključivo
Računarski praktikum I - Vježbe 09 - this, static
 Prirodoslovno-matematički fakultet Matematički odsjek Sveučilište u Zagrebu RAČUNARSKI PRAKTIKUM I Vježbe 09 - this, static v2018/2019. Sastavio: Zvonimir Bujanović Pokazivač this Kako funkcija članica
Prirodoslovno-matematički fakultet Matematički odsjek Sveučilište u Zagrebu RAČUNARSKI PRAKTIKUM I Vježbe 09 - this, static v2018/2019. Sastavio: Zvonimir Bujanović Pokazivač this Kako funkcija članica
Računarski praktikum I - Vježbe 03 - Implementacija strukture string
 Prirodoslovno-matematički fakultet Matematički odsjek Sveučilište u Zagrebu RAČUNARSKI PRAKTIKUM I Vježbe 03 - Implementacija strukture string v2018/2019. Sastavio: Zvonimir Bujanović Stringovi u C-u String
Prirodoslovno-matematički fakultet Matematički odsjek Sveučilište u Zagrebu RAČUNARSKI PRAKTIKUM I Vježbe 03 - Implementacija strukture string v2018/2019. Sastavio: Zvonimir Bujanović Stringovi u C-u String
Microsoft Word - Zadaci za samostalno vjezbanje 4.doc
 Zadaci za samostalno vježbanje 4. Svi zadaci dati ovdje su takvi da se mogu uraditi korištenjem isključivo gradiva prva četiri predavanja i ranije stečenog predznanja na predmetu Osnove računarstva. Zvjezdicom
Zadaci za samostalno vježbanje 4. Svi zadaci dati ovdje su takvi da se mogu uraditi korištenjem isključivo gradiva prva četiri predavanja i ranije stečenog predznanja na predmetu Osnove računarstva. Zvjezdicom
Рационални Бројеви Скуп рационалних бројева 1. Из скупа { 3 4, 2, 4, 11, 0, , 1 5, 12 3 } издвој подскуп: а) природних бројева; б) целих броје
 Рационални Бројеви Скуп рационалних бројева. Из скупа {,,,, 0,,, } издвој подскуп: а) природних бројева; б) целих бројева; в) ненегативних рационалних бројева; г) негативних рационалних бројева.. Запиши
Рационални Бројеви Скуп рационалних бројева. Из скупа {,,,, 0,,, } издвој подскуп: а) природних бројева; б) целих бројева; в) ненегативних рационалних бројева; г) негативних рационалних бројева.. Запиши
Računarski praktikum I - Vježbe 01 - Uvod
 Prirodoslovno-matematički fakultet Matematički odsjek Sveučilište u Zagrebu RAČUNARSKI PRAKTIKUM I Vježbe 01 - Uvod v2018/2019. Sastavio: Zvonimir Bujanović Gradivo i način polaganja Gradivo: osnove jezika
Prirodoslovno-matematički fakultet Matematički odsjek Sveučilište u Zagrebu RAČUNARSKI PRAKTIKUM I Vježbe 01 - Uvod v2018/2019. Sastavio: Zvonimir Bujanović Gradivo i način polaganja Gradivo: osnove jezika
Računarski praktikum I - Vježbe 06 - Standard Template Library (2)
 Prirodoslovno-matematički fakultet Matematički odsjek Sveučilište u Zagrebu RAČUNARSKI PRAKTIKUM I Vježbe 06 - Standard Template Library (2) v2018/2019. Sastavio: Zvonimir Bujanović pair pair je generička
Prirodoslovno-matematički fakultet Matematički odsjek Sveučilište u Zagrebu RAČUNARSKI PRAKTIKUM I Vježbe 06 - Standard Template Library (2) v2018/2019. Sastavio: Zvonimir Bujanović pair pair je generička
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe
 6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe, očekuje se da su koordinate celobrojne. U slučaju
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe, očekuje se da su koordinate celobrojne. U slučaju
Programiranje 2 0. predavanje Saša Singer web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb Prog2 2019, 0. predavanje p. 1/4
 Programiranje 2 0. predavanje Saša Singer singer@math.hr web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb Prog2 2019, 0. predavanje p. 1/48 Sadržaj predavanja Ponavljanje onog dijela C-a koji
Programiranje 2 0. predavanje Saša Singer singer@math.hr web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb Prog2 2019, 0. predavanje p. 1/48 Sadržaj predavanja Ponavljanje onog dijela C-a koji
Algoritmi SŠ P1
 Županijsko natjecanje iz informatike Srednja škola 9. veljače 2018. RJEŠENJA ZADATAKA Napomena: kodovi za većinu opisanih algoritama dani su u Pythonu radi jednostavnosti i lakše čitljivosti. Zbog prirode
Županijsko natjecanje iz informatike Srednja škola 9. veljače 2018. RJEŠENJA ZADATAKA Napomena: kodovi za većinu opisanih algoritama dani su u Pythonu radi jednostavnosti i lakše čitljivosti. Zbog prirode
PowerPoint Presentation
 Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
CIJELI BROJEVI 1.) Kako još nazivamo pozitivne cijele brojeve? 1.) Za što je oznaka? 2.) Ispiši skup prirodnih brojeva! 3.) Kako označavamo skup priro
 CIJELI BROJEVI 1.) Kako još nazivamo pozitivne cijele brojeve? 1.) Za što je oznaka? 2.) Ispiši skup prirodnih brojeva! 3.) Kako označavamo skup prirodnih brojeva? 4.) Pripada li 0 skupu prirodnih brojeva?
CIJELI BROJEVI 1.) Kako još nazivamo pozitivne cijele brojeve? 1.) Za što je oznaka? 2.) Ispiši skup prirodnih brojeva! 3.) Kako označavamo skup prirodnih brojeva? 4.) Pripada li 0 skupu prirodnih brojeva?
Рачунарска интелигенција
 Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Uvod u takmičarsko programiranje
 8. čas Uvod u programiranje - naredbe ciklusa Uvežbavamo naredbe ciklusa, naredbe ponavljanja (loop) https://studio.code.org/s/course2/stage/6/puzzle/3 "Talk is cheap. Show me the code." - Linus Torvalds
8. čas Uvod u programiranje - naredbe ciklusa Uvežbavamo naredbe ciklusa, naredbe ponavljanja (loop) https://studio.code.org/s/course2/stage/6/puzzle/3 "Talk is cheap. Show me the code." - Linus Torvalds
My_ST_FTNIspiti_Free
 ИСПИТНИ ЗАДАЦИ СУ ГРУПИСАНИ ПО ТЕМАМА: ЛИМЕСИ ИЗВОДИ ФУНКЦИЈЕ ЈЕДНЕ ПРОМЕНЉИВЕ ИСПИТИВАЊЕ ТОКА ФУНКЦИЈЕ ЕКСТРЕМИ ФУНКЦИЈЕ СА ВИШЕ ПРОМЕНЉИВИХ 5 ИНТЕГРАЛИ ДОДАТАК ФТН Испити С т р а н а Лимеси Одредити
ИСПИТНИ ЗАДАЦИ СУ ГРУПИСАНИ ПО ТЕМАМА: ЛИМЕСИ ИЗВОДИ ФУНКЦИЈЕ ЈЕДНЕ ПРОМЕНЉИВЕ ИСПИТИВАЊЕ ТОКА ФУНКЦИЈЕ ЕКСТРЕМИ ФУНКЦИЈЕ СА ВИШЕ ПРОМЕНЉИВИХ 5 ИНТЕГРАЛИ ДОДАТАК ФТН Испити С т р а н а Лимеси Одредити
РЕПУБЛИКА СРПСКА МИНИСТАРСТВО ПРОСВЈЕТЕ И КУЛТУРЕ РЕПУБЛИЧКИ ПЕДАГОШКИ ЗАВОД Милоша Обилића 39 Бањалука, Тел/факс 051/ , 051/ ; p
 РЕПУБЛИКА СРПСКА МИНИСТАРСТВО ПРОСВЈЕТЕ И КУЛТУРЕ РЕПУБЛИЧКИ ПЕДАГОШКИ ЗАВОД Милоша Обилића 9 Бањалука, Тел/факс 01/40-110, 01/40-100; e-mail : pedagoski.zavod@rpz-rs.org Датум: 8.04.018. Републичко такмичење
РЕПУБЛИКА СРПСКА МИНИСТАРСТВО ПРОСВЈЕТЕ И КУЛТУРЕ РЕПУБЛИЧКИ ПЕДАГОШКИ ЗАВОД Милоша Обилића 9 Бањалука, Тел/факс 01/40-110, 01/40-100; e-mail : pedagoski.zavod@rpz-rs.org Датум: 8.04.018. Републичко такмичење
Programiranje II Beleške sa vežbi Smer Informatika Matematički fakultet, Beograd Sana Stojanović 1
 Programiranje II Beleške sa vežbi Smer Informatika Matematički fakultet, Beograd Sana Stojanović 1 Sadržaj 1 Pokazivači - ponavljanje 3 2 Pokazivači - veza sa nizovima 5 2 1 Pokazivači - ponavljanje 1.
Programiranje II Beleške sa vežbi Smer Informatika Matematički fakultet, Beograd Sana Stojanović 1 Sadržaj 1 Pokazivači - ponavljanje 3 2 Pokazivači - veza sa nizovima 5 2 1 Pokazivači - ponavljanje 1.
Maksimalni protok kroz mrežu - Ford-Fulkerson, Edmonds-Karp
 Maksimalni protok kroz mrežu - Ford-Fulkerson, Edmonds-Karp PMF-MO Seminar iz kolegija Oblikovanje i analiza algoritama 22.1.2019. mrežu - Ford-Fulkerson, Edmonds-Karp 22.1.2019. 1 / 35 Uvod - definicije
Maksimalni protok kroz mrežu - Ford-Fulkerson, Edmonds-Karp PMF-MO Seminar iz kolegija Oblikovanje i analiza algoritama 22.1.2019. mrežu - Ford-Fulkerson, Edmonds-Karp 22.1.2019. 1 / 35 Uvod - definicije
Slide 1
 OSNOVNI POJMOVI Naredba je uputa računalu za obavljanje određene radnje. Program je niz naredbi razumljivih računalu koje rješavaju neki problem. Pisanje programa zovemo programiranje. Programski jezik
OSNOVNI POJMOVI Naredba je uputa računalu za obavljanje određene radnje. Program je niz naredbi razumljivih računalu koje rješavaju neki problem. Pisanje programa zovemo programiranje. Programski jezik
I grupa 1. Napisati program koji izračunava i ispisuje zbir 4 najveća od pet brojeva unetih sa standardnog ulaza. ulaz izlaz Analiza: 1.
 I grupa 1. Napisati program koji izračunava i ispisuje zbir 4 najveća od pet brojeva unetih sa standardnog ulaza. ulaz izlaz 3 2 1 4 5 14 Analiza: 1. Odredimo zbir svih 5 unesenih brojeva (i sačuvamo u
I grupa 1. Napisati program koji izračunava i ispisuje zbir 4 najveća od pet brojeva unetih sa standardnog ulaza. ulaz izlaz 3 2 1 4 5 14 Analiza: 1. Odredimo zbir svih 5 unesenih brojeva (i sačuvamo u
Microsoft PowerPoint - Programski_Jezik_C_Organizacija_Izvrsnog_Programa [Compatibility Mode]
![Microsoft PowerPoint - Programski_Jezik_C_Organizacija_Izvrsnog_Programa [Compatibility Mode] Microsoft PowerPoint - Programski_Jezik_C_Organizacija_Izvrsnog_Programa [Compatibility Mode]](/thumbs/100/143599108.jpg) Организација извршног програма (Марић, Јаничић: Програмирање 1, 9.3.3) Извршавање програма После успешног превођења (претпроцесирања, компилације, повезивања) програм може да се изврши Извршавање се захтева
Организација извршног програма (Марић, Јаничић: Програмирање 1, 9.3.3) Извршавање програма После успешног превођења (претпроцесирања, компилације, повезивања) програм може да се изврши Извршавање се захтева
Microsoft PowerPoint - jkoren10.ppt
 Dickey-Fuller-ov test jediničnog korena Osnovna ideja Različite determinističke komponente Izračunavanje test-statistike Pravilo odlučivanja Određivanje broja jediničnih korena Algoritam testiranja Prošireni
Dickey-Fuller-ov test jediničnog korena Osnovna ideja Različite determinističke komponente Izračunavanje test-statistike Pravilo odlučivanja Određivanje broja jediničnih korena Algoritam testiranja Prošireni
JMBAG IME I PREZIME BROJ BODOVA MJERA I INTEGRAL 2. kolokvij 29. lipnja (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni!) 1. (
 MJERA I INTEGRAL. kolokvij 9. lipnja 018. (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni! 1. (ukupno 6 bodova Neka je (, F, µ prostor s mjerom, neka je (f n n1 niz F-izmjerivih funkcija
MJERA I INTEGRAL. kolokvij 9. lipnja 018. (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni! 1. (ukupno 6 bodova Neka je (, F, µ prostor s mjerom, neka je (f n n1 niz F-izmjerivih funkcija
Microsoft PowerPoint - 10-Jednodimenzionalni nizovi.ppt [Compatibility Mode]
![Microsoft PowerPoint - 10-Jednodimenzionalni nizovi.ppt [Compatibility Mode] Microsoft PowerPoint - 10-Jednodimenzionalni nizovi.ppt [Compatibility Mode]](/thumbs/102/155833725.jpg) Osnove programiranja Nizovi Sadržaj Definicija niza Vrste i elementi nizova Deklarisanje nizova Dodele (početne) vrednosti nizovima Jednodimenzionalni nizovi Primeri dodele vrednosti Petlja foreach Nizovi
Osnove programiranja Nizovi Sadržaj Definicija niza Vrste i elementi nizova Deklarisanje nizova Dodele (početne) vrednosti nizovima Jednodimenzionalni nizovi Primeri dodele vrednosti Petlja foreach Nizovi
P1.2 Analiza efikasnosti algoritama 2
 Analiza efikasnosti algoritama II Alg. uređivanja (sortiranja) sa umetanjem elemenata Alg. uređivanja (sortiranja)sa spajanjem podnizova 1 Algoritam uređivanja sa umetanjem elemenata (1/4) Uređivanje ulaznog
Analiza efikasnosti algoritama II Alg. uređivanja (sortiranja) sa umetanjem elemenata Alg. uređivanja (sortiranja)sa spajanjem podnizova 1 Algoritam uređivanja sa umetanjem elemenata (1/4) Uređivanje ulaznog
Programiranje 1 drugi kolokvij, 2. veljače Ime i prezime: JMBAG: Upute: Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i brisanje,
 Upute: Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i brisanje, te službeni podsjetnik. Kalkulatori, mobiteli, razne neslužbene tablice, papiri i sl., nisu dozvoljeni! Sva rješenja napišite
Upute: Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i brisanje, te službeni podsjetnik. Kalkulatori, mobiteli, razne neslužbene tablice, papiri i sl., nisu dozvoljeni! Sva rješenja napišite
My_P_Trigo_Zbir_Free
 Штa треба знати пре почетка решавања задатака? ТРИГОНОМЕТРИЈА Ниво - Основне формуле које произилазе из дефиниција тригонометријских функција Тригонометријске функције се дефинишу у правоуглом троуглу
Штa треба знати пре почетка решавања задатака? ТРИГОНОМЕТРИЈА Ниво - Основне формуле које произилазе из дефиниција тригонометријских функција Тригонометријске функције се дефинишу у правоуглом троуглу
Microsoft Word - 15ms261
 Zadatak 6 (Mirko, elektrotehnička škola) Rješenje 6 Odredite sup S, inf S, ma S i min S u skupu R ako je S = { R } a b = a a b + b a b, c < 0 a c b c. ( ), : 5. Skratiti razlomak znači brojnik i nazivnik
Zadatak 6 (Mirko, elektrotehnička škola) Rješenje 6 Odredite sup S, inf S, ma S i min S u skupu R ako je S = { R } a b = a a b + b a b, c < 0 a c b c. ( ), : 5. Skratiti razlomak znači brojnik i nazivnik
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВН
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2017/2018. година
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2017/2018. година
DISKRETNA MATEMATIKA
 DISKRETNA MATEMATIKA Kombinatorika Permutacije, kombinacije, varijacije, binomna formula Ivana Milosavljević - 1 - 1. KOMBINATORIKA PRINCIPI PREBROJAVANJA Predmet kombinatorike je raspoređivanje elemenata
DISKRETNA MATEMATIKA Kombinatorika Permutacije, kombinacije, varijacije, binomna formula Ivana Milosavljević - 1 - 1. KOMBINATORIKA PRINCIPI PREBROJAVANJA Predmet kombinatorike je raspoređivanje elemenata
The real problem is that programmers have spent far too much time worrying about efficiency in the wrong places and at the wrong times; premature opti
 The real problem is that programmers have spent far too much time worrying about efficiency in the wrong places and at the wrong times; premature optimization is the root of all evil (or at least most
The real problem is that programmers have spent far too much time worrying about efficiency in the wrong places and at the wrong times; premature optimization is the root of all evil (or at least most
Programiranje 1 9. predavanje Saša Singer web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb Prog1 2018, 9. predavanje p. 1/6
 Programiranje 1 9. predavanje Saša Singer singer@math.hr web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb Prog1 2018, 9. predavanje p. 1/60 Sadržaj predavanja Osnovni algoritmi na cijelim brojevima:
Programiranje 1 9. predavanje Saša Singer singer@math.hr web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb Prog1 2018, 9. predavanje p. 1/60 Sadržaj predavanja Osnovni algoritmi na cijelim brojevima:
Grananje u programu predavač: Nadežda Jakšić
 Grananje u programu predavač: Nadežda Jakšić u okviru linijske strukture izvršavaju se sve naredbe u okviru razgranate strukture uvek se ispituje neki uslov; u zavisnosti od toga da li je uslov ispunjen
Grananje u programu predavač: Nadežda Jakšić u okviru linijske strukture izvršavaju se sve naredbe u okviru razgranate strukture uvek se ispituje neki uslov; u zavisnosti od toga da li je uslov ispunjen
Problemi zadovoljavanja ogranicenja.
 I122 Osnove umjetne inteligencije Tema:. 7.1.2016. predavač: Darija Marković asistent: Darija Marković 1 I122 Osnove umjetne inteligencije. 2/26 (PZO) Problem zadovoljavanja ograničenja sastoji se od 3
I122 Osnove umjetne inteligencije Tema:. 7.1.2016. predavač: Darija Marković asistent: Darija Marković 1 I122 Osnove umjetne inteligencije. 2/26 (PZO) Problem zadovoljavanja ograničenja sastoji se od 3
My_P_Red_Bin_Zbir_Free
 БИНОМНА ФОРМУЛА Шт треба знати пре почетка решавања задатака? I Треба знати биному формулу која даје одговор на питање чему је једнак развој једног бинома када га степенујемо са бројем 0 ( ) или ( ) 0!,
БИНОМНА ФОРМУЛА Шт треба знати пре почетка решавања задатака? I Треба знати биному формулу која даје одговор на питање чему је једнак развој једног бинома када га степенујемо са бројем 0 ( ) или ( ) 0!,
PROMENLJIVE, TIPOVI PROMENLJIVIH
 PROMENLJIVE, TIPOVI PROMENLJIVIH Šta je promenljiva? To je objekat jezika koji ima ime i kome se mogu dodeljivati vrednosti. Svakoj promenljivoj se dodeljuje registar (memorijska lokacija) operativne memorije
PROMENLJIVE, TIPOVI PROMENLJIVIH Šta je promenljiva? To je objekat jezika koji ima ime i kome se mogu dodeljivati vrednosti. Svakoj promenljivoj se dodeljuje registar (memorijska lokacija) operativne memorije
Inženjering informacionih sistema
 Fakultet tehničkih nauka, Novi Sad Inženjering informacionih sistema Dr Ivan Luković Dr Slavica Kordić Nikola Obrenović Milanka Bjelica Dr Jelena Borocki Dr Milan Delić UML UML (Unified Modeling Language)
Fakultet tehničkih nauka, Novi Sad Inženjering informacionih sistema Dr Ivan Luković Dr Slavica Kordić Nikola Obrenović Milanka Bjelica Dr Jelena Borocki Dr Milan Delić UML UML (Unified Modeling Language)
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K.
 1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K. Elementi a k K su koeficijenti polinoma P (x). Ako
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K. Elementi a k K su koeficijenti polinoma P (x). Ako
MIP-heuristike (Matheuristike) Hibridi izmedu metaheurističkih i egzaktnih metoda Tatjana Davidović Matematički institut SANU
 MIP-heuristike (Matheuristike) Hibridi izmedu metaheurističkih i egzaktnih metoda Tatjana Davidović Matematički institut SANU http://www.mi.sanu.ac.rs/ tanjad (tanjad@mi.sanu.ac.rs) 21. januar 2013. Tatjana
MIP-heuristike (Matheuristike) Hibridi izmedu metaheurističkih i egzaktnih metoda Tatjana Davidović Matematički institut SANU http://www.mi.sanu.ac.rs/ tanjad (tanjad@mi.sanu.ac.rs) 21. januar 2013. Tatjana
Microsoft Word - 6ms001
 Zadatak 001 (Anela, ekonomska škola) Riješi sustav jednadžbi: 5 z = 0 + + z = 14 4 + + z = 16 Rješenje 001 Sustav rješavamo Gaussovom metodom eliminacije (isključivanja). Gaussova metoda provodi se pomoću
Zadatak 001 (Anela, ekonomska škola) Riješi sustav jednadžbi: 5 z = 0 + + z = 14 4 + + z = 16 Rješenje 001 Sustav rješavamo Gaussovom metodom eliminacije (isključivanja). Gaussova metoda provodi se pomoću
Računarski praktikum I - Vježbe 07 - Podstrukture, const, reference
 Prirodoslovno-matematički fakultet Matematički odsjek Sveučilište u Zagrebu RAČUNARSKI PRAKTIKUM I Vježbe 07 - Podstrukture, const, reference v2018/2019. Sastavio: Zvonimir Bujanović Podstrukture Član
Prirodoslovno-matematički fakultet Matematički odsjek Sveučilište u Zagrebu RAČUNARSKI PRAKTIKUM I Vježbe 07 - Podstrukture, const, reference v2018/2019. Sastavio: Zvonimir Bujanović Podstrukture Član
Algoritmi
 Projektovanje algoritama L09.1. Topološko sortiranje Današnje teme Topološko sortiranje Povezanost grafa jako povezane komponente Minimum Spanning Trees (razapinjuće stablo) Lektira: 22. Elementary Graph
Projektovanje algoritama L09.1. Topološko sortiranje Današnje teme Topološko sortiranje Povezanost grafa jako povezane komponente Minimum Spanning Trees (razapinjuće stablo) Lektira: 22. Elementary Graph
1
 Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Електротехнички факултет Универзитета у Београду Катедра за рачунарску технику и информатику Kолоквијум из Интелигентних система Колоквију
 Електротехнички факултет Универзитета у Београду 19.11.017. Катедра за рачунарску технику и информатику Kолоквијум из Интелигентних система Колоквијум траје h. Напуштање сале дозвољено је након 1h. Употреба
Електротехнички факултет Универзитета у Београду 19.11.017. Катедра за рачунарску технику и информатику Kолоквијум из Интелигентних система Колоквијум траје h. Напуштање сале дозвољено је након 1h. Употреба
P3.2 Paralelno programiranje 2
 Paralelno programiranje II Analiza zavisnosti Struktura algoritma Pomoćne strukture Komunikacioni šabloni 1 4 Koraka paralelizacije programa 2 Evo algoritma. Gde je paralelizam? Dekompozicija zadataka
Paralelno programiranje II Analiza zavisnosti Struktura algoritma Pomoćne strukture Komunikacioni šabloni 1 4 Koraka paralelizacije programa 2 Evo algoritma. Gde je paralelizam? Dekompozicija zadataka
Tutoring System for Distance Learning of Java Programming Language
 Obeležene petlje Obeležene petlje Obeležavanje petlje nekim identifikatorom omogućava da se programski tok usmeri na mesto u programu specificirano tim identifikatorom. Ako se iza naredbi break ili continue
Obeležene petlje Obeležene petlje Obeležavanje petlje nekim identifikatorom omogućava da se programski tok usmeri na mesto u programu specificirano tim identifikatorom. Ako se iza naredbi break ili continue
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ и технолошког развоја ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВН
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ и технолошког развоја ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2018/2019. година
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ и технолошког развоја ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2018/2019. година
Microsoft PowerPoint - Programski_Jezik_C_Organizacija_Izvornog_Programa_I_Greske [Compatibility Mode]
![Microsoft PowerPoint - Programski_Jezik_C_Organizacija_Izvornog_Programa_I_Greske [Compatibility Mode] Microsoft PowerPoint - Programski_Jezik_C_Organizacija_Izvornog_Programa_I_Greske [Compatibility Mode]](/thumbs/104/162384614.jpg) Programski jezik C organizacija izvornog programa Prevođenje Pisanje programa izvorni program Prevođenje programa izvršni program Izvršavanje programa rezultat Faze prevođenja Pretprocesiranje Kompilacija
Programski jezik C organizacija izvornog programa Prevođenje Pisanje programa izvorni program Prevođenje programa izvršni program Izvršavanje programa rezultat Faze prevođenja Pretprocesiranje Kompilacija
Oblikovanje i analiza algoritama 5. predavanje Saša Singer web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb OAA 2017, 5. pr
 Oblikovanje i analiza algoritama 5. predavanje Saša Singer singer@math.hr web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb OAA 2017, 5. predavanje p. 1/68 Sadržaj predavanja Nehomogene rekurzije
Oblikovanje i analiza algoritama 5. predavanje Saša Singer singer@math.hr web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb OAA 2017, 5. predavanje p. 1/68 Sadržaj predavanja Nehomogene rekurzije
070-ALIP2-udzbenik.indb
 0. U uvodnom ćemo poglavlju ponoviti osnove programskog jezika C s kojima smo se susreli u. razredu. U kratkom pregledu navedeni su operatori (aritmetički, relacijski i logički), neke od funkcija iz biblioteka
0. U uvodnom ćemo poglavlju ponoviti osnove programskog jezika C s kojima smo se susreli u. razredu. U kratkom pregledu navedeni su operatori (aritmetički, relacijski i logički), neke od funkcija iz biblioteka
P1.1 Analiza efikasnosti algoritama 1
 Analiza efikasnosti algoritama I Asimptotske notacije Master metoda (teorema) 1 Asimptotske notacije (1/2) Služe za opis vremena izvršenja algoritma T(n) gde je n N veličina ulaznih podataka npr. br. elemenata
Analiza efikasnosti algoritama I Asimptotske notacije Master metoda (teorema) 1 Asimptotske notacije (1/2) Služe za opis vremena izvršenja algoritma T(n) gde je n N veličina ulaznih podataka npr. br. elemenata
VEŽBA 5: KLASE I OBJEKTI U C# Cilj ove vežbe je upoznavanje sa osnovama rada sa klasama i objektima u programskom jeziku C#. Pored toga, bide demonstr
 VEŽBA 5: KLASE I OBJEKTI U C# Cilj ove vežbe je upoznavanje sa osnovama rada sa klasama i objektima u programskom jeziku C#. Pored toga, bide demonstrirana upotreba konstruktora, svojstava, metoda klase,
VEŽBA 5: KLASE I OBJEKTI U C# Cilj ove vežbe je upoznavanje sa osnovama rada sa klasama i objektima u programskom jeziku C#. Pored toga, bide demonstrirana upotreba konstruktora, svojstava, metoda klase,
(Microsoft Word - Dr\236avna matura - studeni osnovna razina - rje\232enja)
 1. C. Imamo redom: I. ZADATCI VIŠESTRUKOGA IZBORA 9 + 7 6 9 + 4 51 = = = 5.1 18 4 18 8 10. B. Pomoću kalkulatora nalazimo 10 1.5 = 63.45553. Četvrta decimala je očito jednaka 5, pa se zaokruživanje vrši
1. C. Imamo redom: I. ZADATCI VIŠESTRUKOGA IZBORA 9 + 7 6 9 + 4 51 = = = 5.1 18 4 18 8 10. B. Pomoću kalkulatora nalazimo 10 1.5 = 63.45553. Četvrta decimala je očito jednaka 5, pa se zaokruživanje vrši
Орт колоквијум
 II колоквијум из Основа рачунарске технике I - 27/28 (.6.28.) Р е ш е њ е Задатак На улазе x, x 2, x 3, x 4 комбинационе мреже, са излазом z, долази четворобитни BCD број. Ако број са улаза при дељењу
II колоквијум из Основа рачунарске технике I - 27/28 (.6.28.) Р е ш е њ е Задатак На улазе x, x 2, x 3, x 4 комбинационе мреже, са излазом z, долази четворобитни BCD број. Ако број са улаза при дељењу
Microsoft Word - ZadaciBacktrackingKombinatorika.doc
 Pretraga sa vraćanjem - backtracking Backtracking algoritmi traže rešenje: 1. metodima pokušaja i sistematskim ispitivanjem svih mogućnosti za konstrukciju rešenja i 2. vraćanjem u slučaju greške. Backtracking
Pretraga sa vraćanjem - backtracking Backtracking algoritmi traže rešenje: 1. metodima pokušaja i sistematskim ispitivanjem svih mogućnosti za konstrukciju rešenja i 2. vraćanjem u slučaju greške. Backtracking
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 018/019. година МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 018/019. година МАТЕМАТИКА
I колоквијум из Основа рачунарске технике I СИ- 2017/2018 ( ) Р е ш е њ е Задатак 1 Тачка А Потребно је прво пронаћи вредности функција f(x
 I колоквијум из Основа рачунарске технике I СИ- / (...) Р е ш е њ е Задатак Тачка А Потребно је прво пронаћи вредности функција f(x, x, x ) и g(x, x, x ) на свим векторима. f(x, x, x ) = x x + x x + x
I колоквијум из Основа рачунарске технике I СИ- / (...) Р е ш е њ е Задатак Тачка А Потребно је прво пронаћи вредности функција f(x, x, x ) и g(x, x, x ) на свим векторима. f(x, x, x ) = x x + x x + x
SKRIPTE EKOF 2019/20 skripteekof.com Lekcija 1: Brojevni izrazi Lekcija 1: Brojevni izrazi Pregled lekcije U okviru ove lekcije imaćete priliku da nau
 Lekcija : Brojevni izrazi Pregled lekcije U okviru ove lekcije imaćete priliku da naučite sledeće: osnovni pojmovi o razlomcima proširivanje, skraćivanje, upoređivanje; zapis razlomka u okviru mešovitog
Lekcija : Brojevni izrazi Pregled lekcije U okviru ove lekcije imaćete priliku da naučite sledeće: osnovni pojmovi o razlomcima proširivanje, skraćivanje, upoređivanje; zapis razlomka u okviru mešovitog
PITANJA I ZADACI ZA II KOLOKVIJUM IZ MATEMATIKE I Pitanja o nizovima Nizovi Realni niz i njegov podniz. Tačka nagomilavanja niza i granična vrednost(l
 PITANJA I ZADACI ZA II KOLOKVIJUM IZ MATEMATIKE I Pitanja o nizovima Nizovi Realni niz i njegov podniz. Tačka nagomilavanja niza i granična vrednost(limes) niza. Svojstva konvergentnih nizova, posebno
PITANJA I ZADACI ZA II KOLOKVIJUM IZ MATEMATIKE I Pitanja o nizovima Nizovi Realni niz i njegov podniz. Tačka nagomilavanja niza i granična vrednost(limes) niza. Svojstva konvergentnih nizova, posebno
Hash, topsort (stack, queue), deque, map Hash 1. За дати низ од n елемената, где је n паран број и n <= 10 6, испитати да ли он може бити подељен на n
 Hash, topsort (stack, queue), deque, map Hash 1. За дати низ од n елемената, где је n паран број и n
Hash, topsort (stack, queue), deque, map Hash 1. За дати низ од n елемената, где је n паран број и n
P2.1 Projektovanje paralelnih algoritama 1
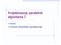 Projektovanje paralelnih algoritama I Uvod Osnove dinamičke paralelizacije 1 Primer: Fibonačijev niz Primer rekurz. računanja Fibonačijevih brojeva: F 0 = 0; F 1 = 1; F i = F i -1 + F i -2 za i 2 Algoritam
Projektovanje paralelnih algoritama I Uvod Osnove dinamičke paralelizacije 1 Primer: Fibonačijev niz Primer rekurz. računanja Fibonačijevih brojeva: F 0 = 0; F 1 = 1; F i = F i -1 + F i -2 za i 2 Algoritam
Упутство за пријављивање испита путем интернета Да би студент могао да пријави испит путем интернета мора прво да се пријави. Пријављивање се врши у п
 Упутство за пријављивање испита путем интернета Да би студент могао да пријави испит путем интернета мора прво да се пријави. Пријављивање се врши у посебном дијалог-прозору до кога се долази линком есервис
Упутство за пријављивање испита путем интернета Да би студент могао да пријави испит путем интернета мора прво да се пријави. Пријављивање се врши у посебном дијалог-прозору до кога се долази линком есервис
Kombinatorno testiranje
 Kombinatorno testiranje Uvod Na ponašanje aplikacije utiče puno faktora, npr. ulazne vrednosti, konfiguracije okruženja. Tehnike kao što je podela na klase ekvivalencije ili analiza graničnih vrednosti
Kombinatorno testiranje Uvod Na ponašanje aplikacije utiče puno faktora, npr. ulazne vrednosti, konfiguracije okruženja. Tehnike kao što je podela na klase ekvivalencije ili analiza graničnih vrednosti
Strukture predavač: Nadežda Jakšić
 Strukture predavač: Nadežda Jakšić složeni tip podatka; kolekcija promenljivih različitog tipa koje su sakupljene radi lakše manipulacije sintaksa: struct [oznakastrukture] navede { definicija člana strukture;
Strukture predavač: Nadežda Jakšić složeni tip podatka; kolekcija promenljivih različitog tipa koje su sakupljene radi lakše manipulacije sintaksa: struct [oznakastrukture] navede { definicija člana strukture;
08 RSA1
 Преглед ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције RSA алгоритам Биће објашњено: RSA алгоритам алгоритам прорачунски аспекти ефикасност коришћењем јавног кључа генерисање кључа сигурност проблем
Преглед ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције RSA алгоритам Биће објашњено: RSA алгоритам алгоритам прорачунски аспекти ефикасност коришћењем јавног кључа генерисање кључа сигурност проблем
Republika Srbija MINISTARSTVO PROSVJETE, NAUKE I TEHNOLOŠKOG RAZVOJA ZAVOD ZA VREDNOVANJE KVALITETA OBRAZOVANJA I ODGOJA ZAVRŠNI ISPIT NA KRAJU OSNOVN
 Republika Srbija MINISTARSTVO PROSVJETE, NAUKE I TEHNOLOŠKOG RAZVOJA ZAVOD ZA VREDNOVANJE KVALITETA OBRAZOVANJA I ODGOJA ZAVRŠNI ISPIT NA KRAJU OSNOVNOG OBRAZOVANJA I ODGOJA školska 2016/2017. godina TEST
Republika Srbija MINISTARSTVO PROSVJETE, NAUKE I TEHNOLOŠKOG RAZVOJA ZAVOD ZA VREDNOVANJE KVALITETA OBRAZOVANJA I ODGOJA ZAVRŠNI ISPIT NA KRAJU OSNOVNOG OBRAZOVANJA I ODGOJA školska 2016/2017. godina TEST
Često postavljana pitanja u programu OBRT 1. Kako napraviti uplatu u knjizi tražbina i obveza? 2. Kako odabrati mapu/disk za pohranu podataka? 3. Kako
 Često postavljana pitanja u programu OBRT 1. Kako napraviti uplatu u knjizi tražbina i obveza? 2. Kako odabrati mapu/disk za pohranu podataka? 3. Kako instalirati (novi) finin certifikat? 4. Kako ispisati
Često postavljana pitanja u programu OBRT 1. Kako napraviti uplatu u knjizi tražbina i obveza? 2. Kako odabrati mapu/disk za pohranu podataka? 3. Kako instalirati (novi) finin certifikat? 4. Kako ispisati
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА О
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Microsoft PowerPoint - OOPpredavanja05 [Compatibility Mode]
![Microsoft PowerPoint - OOPpredavanja05 [Compatibility Mode] Microsoft PowerPoint - OOPpredavanja05 [Compatibility Mode]](/thumbs/88/116292779.jpg) OBJEKTNO ORIJENTISANO PROGRAMIRANJE PREDAVANJE 5 OBJEKTI U INTERAKCIJI Miloš Kovačević Đorđe Nedeljković 1 /25 OSNOVNI KONCEPTI - Abstrakcija - Modularizacija - Objektne reference - Klasni dijagram - Objektni
OBJEKTNO ORIJENTISANO PROGRAMIRANJE PREDAVANJE 5 OBJEKTI U INTERAKCIJI Miloš Kovačević Đorđe Nedeljković 1 /25 OSNOVNI KONCEPTI - Abstrakcija - Modularizacija - Objektne reference - Klasni dijagram - Objektni
OOP1 - domaci 2 (2004/05)
 ЕЛЕКТРОТЕХНИЧКИ ФАКУЛТЕТ Одсеци ИР, ОС и ОФ Београд, 05.04.2019. Први домаћи задатак из Објектно оријентисаног програмирања 2 У сваком задатку: Грешке пријављивати изузецима типа класа које садрже текст
ЕЛЕКТРОТЕХНИЧКИ ФАКУЛТЕТ Одсеци ИР, ОС и ОФ Београд, 05.04.2019. Први домаћи задатак из Објектно оријентисаног програмирања 2 У сваком задатку: Грешке пријављивати изузецима типа класа које садрже текст
ZADACI ZA VJEŽBU 1. Dokažite da vrijedi: (a) (A \ B) (B \ A) = (A B) (A C B C ), (b) A \ (B \ C) = (A C) (A \ B), (c) (A B) \ C = (A \ C) (B \ C). 2.
 ZADACI ZA VJEŽBU. Dokažite da vrijedi: (a) (A \ B) (B \ A) = (A B) (A C B C ), (b) A \ (B \ C) = (A C) (A \ B), (c) (A B) \ C = (A \ C) (B \ C).. Pomoću matematičke indukcije dokažite da za svaki n N vrijedi:
ZADACI ZA VJEŽBU. Dokažite da vrijedi: (a) (A \ B) (B \ A) = (A B) (A C B C ), (b) A \ (B \ C) = (A C) (A \ B), (c) (A B) \ C = (A \ C) (B \ C).. Pomoću matematičke indukcije dokažite da za svaki n N vrijedi:
