Dinamika konstrukcija sa zemljotresnim inžinjerstvom P R E D G O V O R Dinamika konstrukcija sa zemljotresnim inženjerstvom predstavlja veoma aktuelnu
|
|
|
- Dragoljub Petrovič
- пре 6 година
- Прикази:
Транскрипт
1 P R E D G O V O R Dinamika konstrukcija sa zemljotresnim inženjerstvom predstavlja veoma aktuelnu i značajnu oblast Teorije konstrukcija, koja izučava uticaj dinamičkog opterećenja na konstrukcije, posebno zemljotresnog. U knjizi su date osnove neophodne za razumevanje problematike Dinamike konstrukcija i rešavanje problema vezanih za dinamički proračun građevinskih objekata. Knjiga je prvenstveno namenjena i prilagođena studentima akademskih studija građevinskih i arhitektonskih fakulteta. S obzirom da su posle svakog poglavlja urađeni i karakteristični numerički primeri, obrađena materija može biti korisna i inženjerima u praksi. Deo izložene materije se već decenijama izučava na Građevinsko-arhitektonskom fakultetu u Nišu, u okviru predmeta Stabilnost i dinamika konstrukcija na građevinskom, i na drugim predmetima na arhitektonskom smeru. Od godine uvodi se predmet Dinamika konstrukcija sa zemljotresnim inženjerstvom, pa je zemljotresnom inženjerstvu posvećena posebna pažnja. Zbog obimnosti problematike sva razmatranja su ograničena samo na linijske nosače. Predznanje potrebno za razumevanje i praktičnu primenu datog teksta, koji prati i odgovarajuća zbirka rešenih zadataka, je poznavanje tehničke mehanike, statike konstrukcija linijskih nosača i osnove matričnog računa. Zbog specifičnosti seizmičkog opterećenja, a imajući u obzir da se celokupna teritorija naše zemlje nalazi u seizmički aktivnom području, to je ono najčešći oblik dinamičkog opterećenja na građevinske objekte. Iz tih razloga je i izložena materija inženjerske seizmologije i zemljotresnog inženjerstva, sa aspekta adekvatnog korišćenja naših tehničkih propisa iz ove oblasti i Evrokoda 8. U delu zemljotresno inženjerstvo, koje čini posebni i najobimniji deo ove knjige, u dodatku je dat i Evrokod 8, tj. proračun seizmički otpornih konstrukcija. Sadržaj knjige je podeljen u pet delova. Prvi deo je Uvod. U drugom delu detaljno su razmatrani sistemi sa jednim stepenom slobode, gde su objašnjeni osnovni stavovi dinamike konstrukcija. Obrađene su slobodne neprigušene i slobodne prigušene oscilacije. Obrađen je opšti slučaj i specijalni slučajevi i to prinudne oscilacije sa harmonijskom poremećajnom silom. Sistemi sa više stepeni slobode obrađeni su u trećem delu, gde su obrađene slobodne neprigušene oscilacije i metode sračunavanja učestanosti. Velika pažnja je posvećena numeričkim primerima i korišćenju računara u proračunu građevinskih konstrukcija. U daljem tekstu su prikazane prinudne neprigušene oscilacije. Analiza prinudnih prigušenih oscilacija sistema sa više stepeni slobode data je primenom modalne analize. U četvrtom delu obrađeni su sistemi sa kontinualno raspoređenom masom, kao i približno rešavanje sistema sa beskonačno mnogo stepeni slobode. U petom i najobimnijem delu pod nazivom Zemljotresno inženjerstvo obrađena je analiza uticaja zemljtoresa i u Dodatku je prikazan Evrokod 8. 5
2 Pored osnova inženjerske seizmologije, prikazan je i proračun objekata na dejstvo zemljotresa prema važećim tehničkim propisima na karakterističnim numeričkim primerima. Posebno je prikazano određivanje torzionih uticaja na primeru raspodele poprečne sile na zidove nesimetrične zgrade, a dat je i jednostavan model za obuhvatanje popustljivosti tla, tj. interakcije tlo-konstrukcija. Seizmološka karta je data samo za povratni period od 500 godina, jer je ona relevantna za projektovanje objekata visokogradnje svrstanih u II-III kategoriju objekata jer se takvi objekti najčešće grade, a to su stambene zgrade, hoteli, rastorani, javne i industrijske zgrade koje nisu svrstane u prvu kategoriju, kao i pomoćno-proizvodne zgrade i agrotehnički objekti. Potrebno je napomenuti da je značajna pažnja posvećena, u Dodatku, Evrokodu 8: Proračun seizmički otpornih konstrukcija, tj. Evropskom standardu. Bez obzira što je Srbija pridruženi član CEN-a, usvajanje Evropskih standarda je jedan od uslova za ulazak u Evropsku Uniju. Primena ovih propisa u zemljama Evropske zajednice povezana je sa donošenjem Nacionalnog dokumenta za primenu (NAD). Izrada takvog dokumenta u našoj zemlji je potrebna u okviru Evrokoda 8, jer su u četiri zemlje u okruženju već doneti propisi prema Evrokodu 8. Projektovanje i građenje seizmički otpornih konstrukcija u današnje vreme nije više posebno znanje pojedinih stručnjaka i naučnika, već je to deo redovnog obrazovanja građevinskih inženjera. Smatrao sam za potrebnim da buduće inženjere treba još sada upozanti sa Evropskim standardima za zgrade i mostove u delu koji se odnosi na Evrokod 8 (EC8) iako to još uvek nisu naši propisi, i njihova primena nije naša obaveza. Treba imati u vidu da će naši stručnjaci računati i graditi objekte i za inostranstvo, u zemlji i van zemlje. pri čemu je potrebna primena EC8. Pri koncipiranju ovog udžbenika korišćena je knjiga Dinamika konstrukcija izdata zajedno sa profesorom Milićem Milićevićem (1984). Autor očekuje da će ovaj udžbenik pomoći studentima u uspešnom savlađivanju gradiva iz Dinamike konstrukcija i zemljotresnog inženjerstva, a građevinskim inženjerima pomoći pri projektovanju objekata i rešavanju ovih problema u inženjerskoj praksi. Autoru je prijatna dužnost da se zahvali prof. dr Tomislavu Igiću i prof. dr Marini Mijalković, na uloženom trudu i datim sugestijama pri recenziji rukopisa. Autor se zahvaljuje docentu dr Draganu Zlatkovu, kao i kolektivu Projektinžinjering Tim i izdavačkom preduzeću,,agm knjiga za uspešnu realizaciju publikovanja ove knjige. Zapažanja, sugestije i primedbe, ako ih ima, dostaviti autoru koji će ih sa zahvalnošću prihvatiti. Niš, januar godine Autor 6
3 S A D R ŽA J I UVOD II SISTEMI SA JEDNIM STEPENOM SLOBODE Slobodne oscilacije sistema sa jednim stepenom slobode Slobodne neprigušene oscilacije Numerički primeri Slobodne prigušene oscilacije sa viskoznim otporima Numerički primeri Prinudne prigušene oscilacije sistema sa jednim stepenom slobode Opšti slučaj Specijalni slučajevi Prinudne oscilacije sa harmonijskom poremećajnom silom Numerički primeri Eksperimentalno određivanje oscilacija Uticaj naglog opterećenja Opterećenje impulsom Numerički primeri Proizvoljna poremećajna sila Numerički primeri III SISTEMI SA VIŠE STEPENI SLOBODE Slobodne neprigušene oscilacije sistema Diferencijalna jednačina kretanja Rešenje problema slobodnih neprigušenih oscilacija sistema Metode sračunavanja učestanosti Metoda iteracije Metode Stodole i Holcera Metode spektralnih funkcija Numerički primer Prinudne neprigušene oscilacije sistema sa više stepeni slobode Opšti slučaj Slučaj kada su prinudne sile harmonijske, sinhrone i sinfazne funkcije Numerički primeri Analiza prinudnih prigušenih oscilacija sistema sa više stepeni slobode primenom modalne analize Modalna analiza Numerička integracija korak po korak Metoda sa konstantnim ubrzanjem (Newmark-ov postupak) Tačnost i stabilnost metoda numeričkih integracija IV OSCILACIJE SISTEMA SA KONTINUALNO RASPODELJENOM MASOM Osnovne jednačine linijskih nosča u ravni u dinamici konstrukcija Osnovne diferencijalne jednačine štapa u dinamici konstrukcija
4 4.1.2 Osnovne jednačine sistema u dinamici konstrukcija Poprečne oscilacije pravih prizmatičnih štapova Slobodne oscilacije proste grede Slobodne oscilacije konzole Sistemi sa konačnim brojem stepeni slobode Metode zamene kontinualno raspodeljene mase diskretnim skupom koncentrisanih masa Prosta greda Konzolna greda Uklještena greda Torzione oscilacije Primer konzolni nosač kružnog poprečnog preseka V ZEMLJOTRESNO INŽENJERSTVO Uvod Zemljotresi kao prirodni fenomeni Parametri zemljotresa Magnituda zemljotresa i intenzitet zemljotresa Skala seizmičkog intenziteta Medvedev-Sponheuer-Karnik (MSK-64) Kratak prikaz Evropske makroseizmičke skale EMS Vibracije seizmičkih talasa kroz tlo Uticaj vrste tla na stepen seizmičnosti, seizmička rejonizacija i mikrorejonizacija Određivanje seizmičkih sila Metoda direktne dinamičke analize Metoda spektralne analize Sistemi sa jednim stepenom slobode Sprektri odgovora i projektni spektri Projektni spektri Sistemi sa više stepenom slobode Upotreba spektra odgovora Analiza višespratnih sistema spektralnom teorijom Nosivost i duktilnost Osnovna načela u zemljotresnom inženjerstvu Adaptacija i rekonstrukcija postojećih objekata Proračun objekta na dejstvo zemljotresa prema važećim tehničkim propisima Izvodi iz važećih tehničkih propisa za objekte visokogradnje (1981) Osnovni principi projektovanja građevinskih objekata izloženih dejstvu zemljotresa Numerički primeri Primer 1 AB trobrodni okvirni nosač Primer 2a Antenski stub Proračun prema Pravilniku za objekte visokogradnje Primer 2b Antenski stub Proračun prema nacrtu Pravilnika za inženjerske objekte Primer 3 trospratna zgrada Interakcija konstrukcije i tla Jednostavni model za popustljivost tla
5 5.9.2 Formulisanje parametara saradnje tla i konstrukcija na realnim objektima Dodatak EC * Opšta pravila, seizmička dejstva i pravila za zgrade EN : Opšte napomene Zahtevi ponašanja i graničnih stanja Granična stanja Posebne mere pri projektovanju Uslovi tla i zemljotresno dejstvo Uslovi i klasifikacija tipova tla prema EC Seizmičko dejstvo Osnovna prikazivanja zemljotresnog dejstva prema EC Horizontalni elastični spektar odgovora Vertikalni elastični spektar odgovora Projektno pomeranje tla Projektni spektar za elastičnu analizu Alternativna prikazivanja zemljotresnog dejstva Osnovni principi seizmički otpornih konstrukcija zgrada prema EC Izbor konstruktivnog sistema Izbor povoljne konfiguracije zgrade po osnovi i po visini Obezbeđivanje rezervne nosivosti konstruktivnog sistema Analiza konstrukcije Proračunski model Metode analize Kombinacije efekata komponenata seizmičkog dejstva Proračun pomeranja Nenoseći elementi Procena stanja oštećenja i ojačanja zgrada EN : Zahtevi ponašanja i granična stanja Podaci za procenu stanja konstrukcije Procena stanja Odluke o konstrukcijskim intervencijama Projekat konstrukcijske intervencije Deo 3: Informativni aneksi Seizmička analiza mostova Osnovne postavke EN :2004(5) Kontrola ponašanja konstrukcija pri dejstvu zemljotresa Elementi za seizmičku izolaciju i apsorbciju Kontrola kvaliteta gradnje Procena štete Seizmički hazard kao najvažniji element seizmičkog rizika Oznake Indeks pojmova Literatura O autoru
6 10
7 I. UVOD Dinamika konstrukcija je deo Teorije konstrukcija koji se bavi proučavanjem stanja naprezanja i stanja deformacije konstrukcija pri dinamičkom opterećenju na bazi zakona Dinamike. Zavisno od vrste nosača, u Dinamici konstrukcija se može govoriti o dinamici linijskih nosača u ravni i u prostoru, kao i o dinamici površinskih nosača. U zavisnosti od ponašanja materijala pod opterećenjem može se govoriti o elastičnom, plastičnom ili elastoplastičnom ponašanju konstrukcije pri dinamičnom opterećenju. U ovom kursu biće govora o Dinamici elastičnih linijskih nosača u ravni, čije je izučavanje proizašlo uglavnom iz dva razloga: današnje inženjerske konstrukcije su sve elegantnije, odnos stalnog i korisnog opterećenja postaje sve izraženiji u smislu da je uticaj korisnog opterećenja sve dominantniji. S obzirom da su realna statička opterećenja strogo uzevši ne tako česta, a da dinamička opterećenja izazivaju dinamičke uticaje koji su utoliko veći ukoliko su konstrukcije vitkije. veliki deo teritorije naše zemlje leži u seizmički aktivnim područjima, pa zato se nameće potreba da se građevinske konstrukcije analiziraju na uticaj zemljotresa u cilju obezbeđenja njihove sigurnosti i pri ovim uticajima. U Statici konstrukcija opterećenje u toku vremena ne menja ni intenzitet, ni položaj, ni pravac, ni smer. Ono se nanosi na konstrukciju postepeno tako da se u konstrukciji ne pojave značajna ubrzanja čestica (mase) konstrukcije. Intenzitet takvog opterećenja raste od nule do svoje pune vrednosti postupno i zadržava stalni karakter. Dinamička opterećenja su ona koja u toku vremena menjaju ili mogu menjati položaj, intenzitet, pravac i smer. Ovo dovodi do pojave ubrzanja čestica nosača na koji deluju kao i na pojavu inercijalnih sila u nosaču, što ima za posledicu složeniju analizu stanja naprezanja i deformacije koji se pojavljuju u nosačima za razliku od one u Statici konstrukcija. Ova se analiza svodi na dinamički proračun konstrukcija i analizu pojave resonance u konstrukciji. Vrste i podela dinamičkog opterećenja. Osnovne vrste dinamičkog opterećenja su: udarno opterećenje; vibraciono opterećenje. Udarna opterećenja su opterećenja koja se naglo nanose na konstrukciju i ostaju na 11
8 njoj duže ili kraće vreme. Udarno opterećenje može biti periodično i aperiodično. Periodično opterećenje je opterećenje koje se ponavlja u jednakim vremenskim razmacima (t). Posebni slučaj periodičnog opterećenja je harmonijsko periodično opterećenje. Naglo naneto opterećenje takođe pripada dinamičkom opterećenju P(t)= P 0 H(t-t 1 ) gde je sa H(t-t 1 ) obeležena Hevisajdova (Heaviside) funkcija (Slika 1.1). Slika 1.1 Naglo naneto opterećenje - Hevisajdova funkcija Opterećenje konačnim impulsom može se prikazati preko razlike Hevisajdovih funkcija (Slika 1.2). Slika 1.2 Konačni impuls prikazan Hevisajdovom funkcijom Impuls sile takođe spada u udarna opterećenja. On predstavlja proizvod sile (koja deluje veoma kratko vreme, a najčešće je visokog intenziteta) i vremena za koje ta sila deluje. I = P(t)dt (1.1) t 1 Dejstvo impulsa (Slika 1.3) moguće je matematički tretirati uvodeći Dirakovu (Dirac) ili delta (δ) funkciju, nazvanu ponekad i jedinični impuls, koji se obeležava simbolom δ(t-t 1 ). t 2 12
9 Slika 1.3 Dirakova (δ) funkcija jedinični impuls I impuls može biti periodičan. Primer (periodičnog ili aperiodičnog) udarnog opterećenja je i udar kovačkog čekića (Slika 1.4). Slika 1.4 Udarno opterećenje prikazano periodičnim impulsima Naglo izlaganje konstrukcije dejstvu temperature (toplotni udar) izaziva takođe oscilovanje konstrukcije. Vibraciono opterećenje se učestano menja u toku vremena (vibrira), najčešće periodično (Slika 1.5). Ovakvo opterećenje nastaje obično usled rada nekoliko mašina koje su povezane sa rotacijom ekscentrično postavljenih masa. Slika 1.5 Harmonijsko periodično opterećenje 13
10 Vibraciono opterećenje koje se menja po sinusnom ili kosinusnom zakonu naziva se harmonijsko periodično opterećenje. Kada je srednja vrednost ovog opterećenja nula, ono se naziva oscilatorno opterećenje (Slika 1.6). Slika 1.6 Oscilatorno opterećenje Vibraciona opterećenja su nepovoljna zbog toga što i pri malim vrednostima intenziteta opterećenja može doći do loma konstrukcije, ako dođe do pojave rezonance. Do pojave rezonance dolazi onog trenutka kada se frekvencije opterećenja poklope sa nekom od sopstvenih frekvencija sistema. Slučajna (stihijna, stohastička) opterećenja su takva opterećenja koja se kroz vreme menjaju potpuno nepravilno (Slika 1.7). Ona se javljaju pri dejstvu zemljotresa, kao i u nekim drugim slučajevima. Pri matematičkoj analizi ovih problema moraju se koristiti metode numeričke analize, kao i matematičke statistike i računa verovatnoće. Slika 1.7 Slučajno stihijno opterećenje Dinamička temperaturna opterećenja nastaju pri naglom izlaganju konstrukcije dejstvu temperature (na primer pri požaru) izazivajući inercijalnu silu, pa dolazi do pojave njenog oscilovanja. Dinamičko pomeranje oslonaca javlja se pri zemljotresima kada temelji konstrukcije dobijaju pomeranja, odnosno ubrzanja usled seizmičkih talasa, što 14
11 predstavlja najznačajniji vid dinamičkog opterećenja, od izuzetnog značaja u građevinskom konstrukterstvu. Dinamičko opterećenje deluje složenije na konstrukciju od statičkog, pa je i Dinamika konstrukcija složenija od Statike (kao nauke) u izboru i strukturi metoda rešavanja problema. Metode dinamičkog proračuna. Dinamički proračun konstrukcija sastoji se od određivanja unutrašnjih sila i pomeranja usled dinamičkih uticaja poznatih veličina i karaktera, ili od provere sistema na pojavu rezonancije pri periodično promenljivim opterećenjima. Postoji više metoda dinamičkog proračuna, ali se ipak sve one mogu svrstati u dve osnovne grupe i to: statičke metode; energetske metode. Statičke metode se zasnivaju na činjenici da se problemi Dinamike konstrukcija mogu rešavati primenom Dalamberovog (D Alambert) principa ili Langraževih (Lagranže) jednačina kretanja druge vrste, koje se mogu postaviti u obliku jednačina ravnoteže. Energetske metode baziraju se na analizi promene kinetičke i potencijalne energije sistema u toku njegovog kretanja pod dinamičkim opterećenjem i činjenici da je zbir potencijalne i kinetičke energije sistema koji se kreće, pod dejstvom konzervativnih sila, u svakom trenutku vremena konstantna vrednost. Podela sistema prema broju stepeni slobode. U Dinamici konstrukcija, pod brojem stepeni slobode nosača podrazumeva se broj nezavisnih parametara koji određuju pomeranje čvorova u kojima su koncentrisane mase jednog nosača. To znači da je broj stepeni slobode u dinamici konstrukcija određen minimalnim brojem elemenata koje treba dodati dinamičkoj rešetki sistema da bi se sprečilo pomeranje svih čvorova u kojima se nalaze koncentrisane mase. Prema broju stepeni slobode dele se na: sisteme sa jednim stepenom slobode; sisteme sa dva i više stepeni slobode; sisteme sa beskonačno mnogo stepeni slobode. Broj stepeni slobode jednog sistema određuje sa jedne strane njegova geometrija, a sa druge broj masa koje sačinjavaju taj sistem. U osnovi svi sistemi sa kontinualno raspodeljenom masom su sa beskonačno mnogo stepeni slobode. Međutim, u zavisnosti od masa nosača i korisnog opterećenja, vrlo često se može ili masa nosača potpuno zanemariti ili na neki drugi način približno uzeti u obzir, a time i broj stepeni slobode svesti na konačan. Primeri: Zanemarujući sopstvenu težinu nosača, mase u ravni na Slici 1.8 imaju po dva stepena slobode. 15
12 Slika 1.8 Sistemi sa dva stepena slobode Zavisno od karaktera oscilacija, tj. od fizičkih osobina nosača, često se uzima u obzir pretpostavka da se pomeranja u pravcu ose štapa mogu zanemariti, što je ekvivalentno zanemarenju dejstva normalnih sila. Posle uvođenja ove pretpostavke broj stepeni slobode se smanjuje na po jedan stepen slobode svake mase, pa shodno tome sistemi na Slici 1.9 imaju po jedan stepen slobode. Slika 1.9 Sistemi sa jednim stepenom slobode Međutim, zanemarenja pomeranja u pravcu ose štapa nisu uvek moguća, kao na primer kod sistema na Slici Slika 1.10 Sistemi kod kojih je dejstvo u pravcu ose štapa S obzirom da kod primera na Slici 1.10 postoje pomeranja samo u pravcu ose štapa, tj. uzdužne oscilacije, to se one ne mogu zanemariti jer su jedine. Primeri na Slici 1.11 su sistemi sa dva stepena slobode, dok je sistem na Slici 1.12 sa beskonačnim brojem stepeni slobode. Slika 1.11 Sistemi sa dva stepena slobode sa jednom ili sa dve mase 16
13 Slika 1.12 Sistem sa beskonačnim brojem stepeni slobode Oscilovanje sistema tj. čestice (mase). Svi realni nosači se pod uticajem bilo kakvog opterećenja deformišu, tj. mase se pomeraju. Pod dinamičkim opterećenjem mase nosača se takođe pomeraju, ali s obzirom na karakter opterećenja i pod pretpostavkom da je nosač sposoban da primi takvo opterećenje ta su pomeranja masa nosača najčešće oscilatorna kretanja oko položaja statičke ravnoteže. Prema načinu delovanja spoljašnjih uzroka koji ih izazivaju, ove oscilacije delimo na dve osnovne grupe: slobodne (sopstvene) oscilacije, prinudne oscilacije. Slobodne (sopstvene) oscilacije nastaju kada se sistem na bilo koji način izvede iz stanja statičke ravnoteže, a zatim prepusti sam sebi. Nadalje na sistem ne deluju nikakve spoljašnje sile i on vrši slobodne ili sopstvene oscilacije. Prinudne oscilacije su one oscilacije pri kojima sistem osciluje zajedno sa dinamičkim opterećenjem koje trajno ostaje na njemu i u tom slučaju je prinuđen da stalno vrši oscilacije uz prisustvo dinamičkog opterećenja. Prema sredini u kojoj se događaju, oscilacije mogu biti: neprigušene neamortizovane oscilacije, prigušene amortizovane oscilacije. Neprigušene oscilacije, za razliku od prigušenih, nastaju onda kada se u toku vremena ne pojavljuju nikakvi otpori sredine u kojoj se vrše ove oscilacije, ne pojavljuju se otporne sile, tj. sredina je idealna. U realnoj sredini takve oscilacije ne postoje, jer se javljaju otporne sile koje žele da spreče ili umanje ovo kretanje. Pod sredinom se podrazumeva medijum u kome se nalazi analizirani nosač. Takođe se i sam nosač, zavisno od unutrašnjih otpora i osobina materijala suprotstavlja oscilovanju. I sopstvene i prinudne oscilacije mogu biti neprigušene i prigušene. Zemljotresno inženjerstvo izučava dejstvo seizmičkog opterećenja a to je stihijno kretanje, udari i vibracije usled delovanja zemljotresa. Pri ovome dolazi do dinamičkog pomeranja oslonca, tj. do pomeranja konstrukcije. Dinamičke metode za analizu prinudnih vibracija koje nastaju usled pomeranja tla izučavaju ponašanje odgovora dinamičkih modela, pa se tako došlo do nekih zaključaka o zavisnosti maksimalnog ubrzanja od perioda svojstvenih frekvencija. Takvim postupkom je dobijen niz tzv. spektara odgovora (odzivnih spektara, response spectra ), koji pokazuju maksimalne amplitude u funkciji bilo pomeranja, bilo napona, bilo 17
14 ubrzanja itd. svih mogućih linijskih sistema sa jednim stepenom slobode u odnosu na neki dati uzrok, na primer pomeranje tla. Dakle, spektar odgovora pokazuje kako neki dinamički sistem reaguje pri različitim vrednostima sopstvenih frekvencija i odgovarajućeg prigušenja. Korišćenjem metode razvijanja prinudnih vibracija kod diskretnih sistema sa n stepeni slobode po sopstvenim oblicima (tonovima) i primenom spectra odgovora može se vršiti proračun objekata na zemljotresne uticaje. Zemljotresno inženjerstvo je grana inženjerstva posvećena smanjenju, odnosno ublažavanju seizmičkog rizika kroz planiranje, projektovanje, građenje i upravljanje objektima i opremom čija se otpornost na zemljotres zahteva i uslovljava. To je jedna veoma kompleksna i široka oblast, sa mnogo specifičnosti u odnosu na ostala inženjerska područja, počev od socio-humanitarnih preko tehničkih do onih koje izražavaju ekonomsku moć zemlje, odnosno regiona sa aspekta prihvatljivog nivoa seizmičkog rizika. U vezi sa prethodnim treba naglasiti da racionalno planiranje i projektovanje objekata otpornih na zemljotres počiva na multidisciplinarnosti. Mnogo raznih disciplina uključeno je u ovu oblast kao što su: građevinsko-konstruktivno inženjerstvo, seizmologija, geologija, ekonomija, društvene nauke, arhitektura, prostorno-urbanističko planiranje, javna politika itd. Prema navedenom potrebno je ispuniti dva najvažnija osnovna zahteva kod projektovanja seizmički otpornih objekata. Prvi zahtev je da u slučaju zemljotresa gubici ljudskih života, broj povređenih i ukupno oštećenje budu minimalni. Drugi zahtev je da troškovi opravke, odnosno rehabilitacije oštećenih objekata ne bi trebalo da prevaziđu uvećane troškove projektovanja, izgradnje i finansiranja. Napred navedeno moglo bi se preduprediti adekvatnijim konstruisanjem objekata otpornih na dejstvo seizmičkih uticaja. 18
15 5.12 Seizmički hazard kao najvažniji element seizmičkog rizika Za potrebe projektovanja i proračuna uticaja seizmičkih sila najvažniji je seizmički hazard maksimalnog horizontalnog ubrzanja oscilovanja tla za vreme zemljotresa. Seizmički hazard definisan je sa tri međusobno zavisna elementa, veličinom parametra oscilovanja tla, povratnim periodom i verovatnoćom realizacije takvog događaja, uzimanjem u obzir brojne podatke i primenu određenog matematičkog postupka. Nivo seizmičkog rizika predstavlja povredljivost objekta, odnosno urbanog elementa za odgovarajući povratni vremenski period, nivo i verovatnoću pobude. Često se u svakodnevnoj inženjerskoj praksi, ponekad i u stručnoj literaturi, poistovećuju pojmovi seizmičkog rizika i seizmičkog hazarda, iako ovi termini imaju sasvim različito značenje u definisanju zemljotresa kao prirodnog fenomena. Pristup u borbi protiv ove nepogode (stihije) odvija se u tri pravca i to: svestrano izučavanje prirode samog fenomena ( ognjišna seizmologija ), izučavanje interakcije geološke sredine, zemljotresa i objekata ( površinska seizmologija ) i izučavanje građevinskih konstrukcija u uslovima dinamičkog opterećenja ( zemljotresno inženjerstvo ). Izučavanje ovog veoma složenog fenomena podrazumeva multidisciplinarni i u isto vreme interdisciplinarni pristup. Sam proces pojavljivanja zemljotresa sa statističkog aspekta predstavlja jedan stohastički proces, odnosno matematičkki model datog fizičkog sistema koji se menja u saglasnosti sa zakonom verovatnoće (Lomnitz, 1976). Kao metoda za proračun seizmičkog hazarda, koji uključuje i primenu Poisson-ovog modela generisanja potresa, usvojena je metoda Algermisena (UNESCO, 1975). Poissonov statistički proces predstavlja stohastički proces koji izražava položaj pojedinog slučajnog događaja (u ovom slučaju zemljotresa) u vremenu pa se koristi pri proračunu seizmičkog hazarda: x m m e P = (1) x! Ista takva formula koristi se kod određivanja verovatnosti pojave (n) zemljotresa, određene magnitude (M) u vremenu (t), koja se piše u obliku: n λ (M) t ( nt ) e λ P( nt,, λ ) = (2) n! gde je: P( nt,, λ ) - verovatnoća pojave (n) potresa magnitude veće ili jednake (M) n - broj zemljotresa, 299
16 m λ - broj ponovljivih slučajeva, - srednja veličina broja zemljotresa određene magnitude u jedinici vremena (1 godina). Na taj način ( λ ) je jednako (N). Pošto je veza između učestanosti pojavljivanja, odnosno broja zemljotresa (N) i magnitudee (M) data izrazom: log N = a bm (3) ( ) 10 a N = bm, a N = λ, dobija se: P ( nt,, λ ) 10 = n ( a bm ) 10( a bm ) t e n! gde je: N - broj potresa određene magnitude M za određeni broj godina, ab, - konstante relacije koje karakterišu datu žarišnu oblast. Za određivanje verovatnoće pojave zemljotresa najvažnije je odrediti odnos između magnitude zemljotresa i učestanosti pojavljivanja zemljotresa. Poisson-ov model, kako je već rečeno, se najčešće koristi kod proračuna seizmičkog hazarda, odnosno određivanja verovatnoće pojave akceleracije. U tom slučaju umesto magnitude (M), uzima se akceleracija izazvana tom magnitudom, a odnos između njih određuje se odgovarajućom atenuacionom funkcijom. Zemljotres se ne može sprečiti ali se njegove posledice mogu umanjiti. Seizmički rizik se definiše kao očekivani stepen gubitaka prouzrokovanih efektima zemljotresa: rušenjem i oštećenjem objekata, povredama i gubicima ljudskih života, direktnim i indirektnim ekonomskim, funkcionalnim, socijalnim i drugim štetama. Seizmički hazard definiše se kao deo prirodnog hazarda i predstavlja verovatnoću pojavljivanja zemljotresa odgovarajućih karakteristika (intenzitet, brzina, ubrzanje oscilovanja tla itd.) u određenom periodu na određenom mestu. F ( nat,,) n λ ( at ) λ( a) t e = (5) n! Znači verovatnoća da se u vremenu (t) dogodi (n) akceleracija sa iznosom većim ili jednakim ( a ), data je izrazom (5). Osnovni integrativni aspekti smanjenja seizmičkog rizika, tretirajući ih istovremeno i kao bitne elemente jedinstvenog integralnog koncepta, mogu se označiti: 1) utvrđivanje seizmičkog hazarda, 2) aseizmičko projektovanje, 3) prostorno-urbanističko planiranje, 4) mitigacija (umanjenje) seizmičkog rizika, 5) pripremljenost na zemljotres i 6) upravljanje seizmičkim rizikom, kako bi se 300 (4)
17 neprihvatljiv rizik smanjio na prihvatljive nivoe. Prilikom zaštite od dejstva zemljotresa mora se imati poseban osvrt na neka relevantna etička pitanja koja su u neposrednoj vezi sa zemljotresnim inženjerstvom i seizmičkim rizikom uopšte, što se čini iz veoma opravdanih i krajnje aktuelnih razloga, jer je čovekov život neponovljiv, nemerljiv i neprocenjiv. Eksperimentalno ispitivanje objekta u prirodnoj veličini vrši se pomoću generatora vibracija, ambijent vibracijama ili na vibro platformi. 301
Predavanje 8-TEMELJI I POTPORNI ZIDOVI.ppt
 1 BETONSKE KONSTRUKCIJE TEMELJI OBJEKATA Prof. dr Snežana Marinković Doc. dr Ivan Ignjatović Semestar: V ESPB: Temelji objekata 2 1.1. Podela 1.2. Temelji samci 1.3. Temeljne trake 1.4. Temeljne grede
1 BETONSKE KONSTRUKCIJE TEMELJI OBJEKATA Prof. dr Snežana Marinković Doc. dr Ivan Ignjatović Semestar: V ESPB: Temelji objekata 2 1.1. Podela 1.2. Temelji samci 1.3. Temeljne trake 1.4. Temeljne grede
Динамика крутог тела
 Динамика крутог тела. Задаци за вежбу 1. Штап масе m и дужине L се крајем А наслања на храпаву хоризонталну раван, док на другом крају дејствује сила F константног интензитета и правца нормалног на штап.
Динамика крутог тела. Задаци за вежбу 1. Штап масе m и дужине L се крајем А наслања на храпаву хоризонталну раван, док на другом крају дејствује сила F константног интензитета и правца нормалног на штап.
5 - gredni sistemi
 Гредни системи бетонских мостова 1 БЕТОНСКИ МОСТОВИ ГРЕДНИ СИСТЕМИ Типови гредних система бетонских мостова Решетка Проста греда Греда с препустима Герберова греда Континуална греда Укљештена греда 2 Трајекторије
Гредни системи бетонских мостова 1 БЕТОНСКИ МОСТОВИ ГРЕДНИ СИСТЕМИ Типови гредних система бетонских мостова Решетка Проста греда Греда с препустима Герберова греда Континуална греда Укљештена греда 2 Трајекторије
Microsoft PowerPoint - fizika 9-oscilacije
 Предиспитне обавезе Шема прикупљања поена - измене Активност у току предавања = 5 поена (са више од 3 одсуствовања са предавања се не могу добити) Лабораторијске вежбе = 10 поена обавезни сви поени односно
Предиспитне обавезе Шема прикупљања поена - измене Активност у току предавања = 5 поена (са више од 3 одсуствовања са предавања се не могу добити) Лабораторијске вежбе = 10 поена обавезни сви поени односно
Ravno kretanje krutog tela
 Ravno kretanje krutog tela Brzine tačaka tela u reprezentativnom preseku Ubrzanja tačaka u reprezentativnom preseku Primer određivanja brzina i ubrzanja kod ravnog mehanizma Ravno kretanje krutog tela
Ravno kretanje krutog tela Brzine tačaka tela u reprezentativnom preseku Ubrzanja tačaka u reprezentativnom preseku Primer određivanja brzina i ubrzanja kod ravnog mehanizma Ravno kretanje krutog tela
Rešetkasti nosači
 Elementi opterećeni savijanjem - nosači Metalne konstrukcije 1 P6-1 Slučajevi naprezanja Savijanje dominantan vid naprezanja! Savijanje može biti posledica sledećih naprezanja: čisto pravo savijanje (M
Elementi opterećeni savijanjem - nosači Metalne konstrukcije 1 P6-1 Slučajevi naprezanja Savijanje dominantan vid naprezanja! Savijanje može biti posledica sledećih naprezanja: čisto pravo savijanje (M
Pojam konstrukcije, izbor konstruktivnog sistema, konstruktivni sistemi kroz istoriju. Linijski konstruktivni elementi grede,definicija, opšte
 Pojam konstrukcije, izbor konstruktivnog sistema, konstruktivni sistemi kroz istoriju. Linijski konstruktivni elementi grede,definicija, opšte o grednim elementima, karakteristike, statički sistemi, oslonci,
Pojam konstrukcije, izbor konstruktivnog sistema, konstruktivni sistemi kroz istoriju. Linijski konstruktivni elementi grede,definicija, opšte o grednim elementima, karakteristike, statički sistemi, oslonci,
Microsoft PowerPoint - STABILNOST KONSTRUKCIJA 2_18 [Compatibility Mode]
![Microsoft PowerPoint - STABILNOST KONSTRUKCIJA 2_18 [Compatibility Mode] Microsoft PowerPoint - STABILNOST KONSTRUKCIJA 2_18 [Compatibility Mode]](/thumbs/99/140947091.jpg) 6. STABILNOST KONSTRUKCIJA II čas Marija Nefovska-Danilović 3. Stabilnost konstrukcija 1 6.2 Osnovne jednačine štapa 6.2.1 Linearna teorija štapa Važe pretpostavke o geometrijskoj (1), statičkoj (2) i
6. STABILNOST KONSTRUKCIJA II čas Marija Nefovska-Danilović 3. Stabilnost konstrukcija 1 6.2 Osnovne jednačine štapa 6.2.1 Linearna teorija štapa Važe pretpostavke o geometrijskoj (1), statičkoj (2) i
CVRSTOCA
 ČVRSTOĆA 12 TEORIJE ČVRSTOĆE NAPREGNUTO STANJE Pri analizi unutarnjih sila koje se pojavljuju u kosom presjeku štapa opterećenog na vlak ili tlak, pri jednoosnom napregnutom stanju, u tim presjecima istodobno
ČVRSTOĆA 12 TEORIJE ČVRSTOĆE NAPREGNUTO STANJE Pri analizi unutarnjih sila koje se pojavljuju u kosom presjeku štapa opterećenog na vlak ili tlak, pri jednoosnom napregnutom stanju, u tim presjecima istodobno
Матрична анализа конструкција
 . 5 ПРИМЕР На слици. је приказан носач који је састављен од три штапа. Хоризонтални штапови су константног попречног пресека b/h=./.5 m, док је коси штап са линеарном променом висине. Одредити силе на
. 5 ПРИМЕР На слици. је приказан носач који је састављен од три штапа. Хоризонтални штапови су константног попречног пресека b/h=./.5 m, док је коси штап са линеарном променом висине. Одредити силе на
Proracun strukture letelica - Vežbe 6
 University of Belgrade Faculty of Mechanical Engineering Proračun strukture letelica Vežbe 6 15.4.2019. Mašinski fakultet Univerziteta u Beogradu Danilo M. Petrašinović Jelena M. Svorcan Miloš D. Petrašinović
University of Belgrade Faculty of Mechanical Engineering Proračun strukture letelica Vežbe 6 15.4.2019. Mašinski fakultet Univerziteta u Beogradu Danilo M. Petrašinović Jelena M. Svorcan Miloš D. Petrašinović
PRIMER 1 ISPITNI ZADACI 1. ZADATAK Teret težine G = 2 [kn] vezan je užadima DB i DC. Za ravnotežni položaj odrediti sile u užadima. = 60 o, β = 120 o
![PRIMER 1 ISPITNI ZADACI 1. ZADATAK Teret težine G = 2 [kn] vezan je užadima DB i DC. Za ravnotežni položaj odrediti sile u užadima. = 60 o, β = 120 o PRIMER 1 ISPITNI ZADACI 1. ZADATAK Teret težine G = 2 [kn] vezan je užadima DB i DC. Za ravnotežni položaj odrediti sile u užadima. = 60 o, β = 120 o](/thumbs/102/155855156.jpg) PRIMER 1 ISPITNI ZADACI Teret težine G = 2 [kn] vezan je užadima DB i DC. Za ravnotežni položaj odrediti sile u užadima. = 60 o, β = 120 o Homogena pločica ACBD, težine G, sa težištem u tački C, dobijena
PRIMER 1 ISPITNI ZADACI Teret težine G = 2 [kn] vezan je užadima DB i DC. Za ravnotežni položaj odrediti sile u užadima. = 60 o, β = 120 o Homogena pločica ACBD, težine G, sa težištem u tački C, dobijena
Slide 1
 Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
Microsoft Word - TPLJ-januar 2017.doc
 Београд, 21. јануар 2017. 1. За дату кружну плочу која је еластично укљештена у кружни прстен и оптерећења према слици одредити максимални напон у кружном прстену. М = 150 knm/m p = 30 kn/m 2 2. За зидни
Београд, 21. јануар 2017. 1. За дату кружну плочу која је еластично укљештена у кружни прстен и оптерећења према слици одредити максимални напон у кружном прстену. М = 150 knm/m p = 30 kn/m 2 2. За зидни
Зборник радова 6. Међународне конференције о настави физике у средњим школама, Алексинац, март Одређивање коефицијента пригушења у ваздуху
 Одређивање коефицијента пригушења у ваздуху помоћу линеарног хармонијског осцилатора Соња Ковачевић 1, Милан С. Ковачевић 2 1 Прва крагујевачка гимназија, Крагујевац, Србија 2 Природно-математички факултет,
Одређивање коефицијента пригушења у ваздуху помоћу линеарног хармонијског осцилатора Соња Ковачевић 1, Милан С. Ковачевић 2 1 Прва крагујевачка гимназија, Крагујевац, Србија 2 Природно-математички факултет,
ma??? - Primer 1 Spregnuta ploca
 Primer 1 - proračun spregnute ploče na profilisanom limu 1. Karakteristike spregnute ploče Spregnuta ploča je raspona 4 m. Predviđen je jedan privremeni oslonac u polovini raspona ploče u toku građenja.
Primer 1 - proračun spregnute ploče na profilisanom limu 1. Karakteristike spregnute ploče Spregnuta ploča je raspona 4 m. Predviđen je jedan privremeni oslonac u polovini raspona ploče u toku građenja.
Београд, МАТРИЧНА АНАЛИЗА КОНСТРУКЦИЈА ЗАДАТАК 1 За носач приказан на слици: а) одредити дужине извијања свих штапова носача, ако на носач
 Београд, 30.01.2016. а) одредити дужине извијања свих штапова носача, ако на носач делују само концентрисане силе, б) ако је P = 0.8P cr, и на носач делује расподељено оптерећење f, одредити моменат савијања
Београд, 30.01.2016. а) одредити дужине извијања свих штапова носача, ако на носач делују само концентрисане силе, б) ако је P = 0.8P cr, и на носач делује расподељено оптерећење f, одредити моменат савијања
Pismeni ispit iz MEHANIKE MATERIJALA I - grupa A 1. Kruta poluga AB, oslonjena na oprugu BC i okačena o uže BD, nosi kontinuirano opterećenje, kao što
 Pismeni ispit iz MEHNIKE MTERIJL I - grupa 1. Kruta poluga, oslonjena na oprugu i okačena o uže D, nosi kontinuirano opterećenje, kao što je prikazano na slici desno. Odrediti: a) silu i napon u užetu
Pismeni ispit iz MEHNIKE MTERIJL I - grupa 1. Kruta poluga, oslonjena na oprugu i okačena o uže D, nosi kontinuirano opterećenje, kao što je prikazano na slici desno. Odrediti: a) silu i napon u užetu
РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена ) Прва година: ПРВА ГОДИНА - сви сем информатике Име пр
 РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена 23.01.2017.) Прва година: ПРВА ГОДИНА - сви сем информатике Име предмета Датум и термин одржавања писменог дела испита
РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена 23.01.2017.) Прва година: ПРВА ГОДИНА - сви сем информатике Име предмета Датум и термин одржавања писменог дела испита
M e h a n i k a 1 v e ž b e 4 / 2 9 Primer 3.5 Za prostu gredu prikazanu na slici odrediti otpore oslonaca i nacrtati osnovne statičke dijagrame. Pozn
 M e h a n i k a 1 v e ž b e 4 / 9 Primer 3.5 Za prostu gredu prikazanu na slici odrediti otpore oslonaca i nacrtati osnovne statičke dijagrame. Poznata su opterećenja F 1 = kn, F = 1kN, M 1 = knm, q =
M e h a n i k a 1 v e ž b e 4 / 9 Primer 3.5 Za prostu gredu prikazanu na slici odrediti otpore oslonaca i nacrtati osnovne statičke dijagrame. Poznata su opterećenja F 1 = kn, F = 1kN, M 1 = knm, q =
Испитни задаци - Задатак 1 Задатак 1 (23. септембар 2012.) а) Статичком методом конструисати утицајне линије за силе у штаповима V b и D 4. б) Одредит
 Испитни задаци - Задатак 1 Задатак 1 (23. септембар 2012.) а) Статичком методом конструисати утицајне линије за силе у штаповима V b и D 4. б) Одредити max D 4 услед задатог покретног система концентрисаних
Испитни задаци - Задатак 1 Задатак 1 (23. септембар 2012.) а) Статичком методом конструисати утицајне линије за силе у штаповима V b и D 4. б) Одредити max D 4 услед задатог покретног система концентрисаних
( )
 Заштита животне средине Основе механике (кратак преглед предмета) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj 1. Информациjе о предмету
Заштита животне средине Основе механике (кратак преглед предмета) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj 1. Информациjе о предмету
9. : , ( )
 9. Динамика тачке: Енергиjа, рад и снага (први део) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj - Шта ћемо научити (1) 1. Преглед литературе
9. Динамика тачке: Енергиjа, рад и снага (први део) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj - Шта ћемо научити (1) 1. Преглед литературе
Kvadrupolni maseni analizator, princip i primena u kvali/kvanti hromatografiji
 Kvadrupolni maseni analizator, princip i primena u kvali/kvanti hromatografiji doc dr Nenad Vuković, Institut za hemiju, Prirodno-matematički fakultet u Kragujevcu JONIZACIJA ELEKTRONSKIM UDAROM Joni u
Kvadrupolni maseni analizator, princip i primena u kvali/kvanti hromatografiji doc dr Nenad Vuković, Institut za hemiju, Prirodno-matematički fakultet u Kragujevcu JONIZACIJA ELEKTRONSKIM UDAROM Joni u
Microsoft PowerPoint - STABILNOST KONSTRUKCIJA 4_19 [Compatibility Mode]
![Microsoft PowerPoint - STABILNOST KONSTRUKCIJA 4_19 [Compatibility Mode] Microsoft PowerPoint - STABILNOST KONSTRUKCIJA 4_19 [Compatibility Mode]](/thumbs/99/141489570.jpg) Univerzitet u Beogradu Građevinski fakutet Katedra za tehničku mehaniku i teoriju konstrukcija STABILNOST KONSTRUKCIJA IV ČAS V. PROF. DR MARIJA NEFOVSKA DANILOVIĆ 3. SABILNOST KONSTRUKCIJA 1 Geometrijska
Univerzitet u Beogradu Građevinski fakutet Katedra za tehničku mehaniku i teoriju konstrukcija STABILNOST KONSTRUKCIJA IV ČAS V. PROF. DR MARIJA NEFOVSKA DANILOVIĆ 3. SABILNOST KONSTRUKCIJA 1 Geometrijska
STABILNOST SISTEMA
 STABILNOST SISTEMA Najvaznija osobina sistema automatskog upravljanja je stabilnost. Generalni zahtev koji se postavlja pred projektanta jeste da projektovani i realizovani sistem automatskog upravljanja
STABILNOST SISTEMA Najvaznija osobina sistema automatskog upravljanja je stabilnost. Generalni zahtev koji se postavlja pred projektanta jeste da projektovani i realizovani sistem automatskog upravljanja
1
 Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
TEORIJA SIGNALA I INFORMACIJA
 Multiple Input/Multiple Output sistemi MIMO sistemi Ulazi (pobude) Izlazi (odzivi) u 1 u 2 y 1 y 2 u k y r Obrada=Matematički model Načini realizacije: fizički sistemi (hardware) i algoritmi (software)
Multiple Input/Multiple Output sistemi MIMO sistemi Ulazi (pobude) Izlazi (odzivi) u 1 u 2 y 1 y 2 u k y r Obrada=Matematički model Načini realizacije: fizički sistemi (hardware) i algoritmi (software)
Microsoft Word - 7. cas za studente.doc
 VII Диферeнцни поступак Користи се за решавање диференцијалних једначина. Интервал на коме је дефинисана тражена функција се издели на делова. Усвоји се да се непозната функција између сваке три тачке
VII Диферeнцни поступак Користи се за решавање диференцијалних једначина. Интервал на коме је дефинисана тражена функција се издели на делова. Усвоји се да се непозната функција између сваке три тачке
M e h a n i k a 1 v e ž b e 4 /1 1 Primer 3.1 Za prostu gredu prikazanu na slici odrediti otpore oslonaca i nacrtati osnovne statičke dijagrame. q = 0
 M e h a n i k a 1 v e ž b e 4 /1 1 Primer 3.1 Za prostu gredu prikazanu na slici odrediti otpore oslonaca i nacrtati osnovne statičke dijagrame. q = 0.8 kn m, L=4m. 1. Z i = Z A = 0. Y i = Y A L q + F
M e h a n i k a 1 v e ž b e 4 /1 1 Primer 3.1 Za prostu gredu prikazanu na slici odrediti otpore oslonaca i nacrtati osnovne statičke dijagrame. q = 0.8 kn m, L=4m. 1. Z i = Z A = 0. Y i = Y A L q + F
ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 2006/2007 године I разред
 ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 006/007 године разред. Електрични систем се састоји из отпорника повезаних тако
ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 006/007 године разред. Електрични систем се састоји из отпорника повезаних тако
ИСПИТНА ПИТАЊА ЗА ПРВИ КОЛОКВИЈУМ 1. Шта проучава биофизика и навести бар 3 области биофизике 2. Основне физичке величине и њихове јединице 3. Појам м
 ИСПИТНА ПИТАЊА ЗА ПРВИ КОЛОКВИЈУМ 1. Шта проучава биофизика и навести бар 3 области биофизике 2. Основне физичке величине и њихове јединице 3. Појам материјалне тачке 4. Појам механичког система 5. Појам
ИСПИТНА ПИТАЊА ЗА ПРВИ КОЛОКВИЈУМ 1. Шта проучава биофизика и навести бар 3 области биофизике 2. Основне физичке величине и њихове јединице 3. Појам материјалне тачке 4. Појам механичког система 5. Појам
ZBIRKA TBK FIN_bez oznaka za secenje.pdf
 ZBIRKA ZADATAKA TEORIJA BETONSKIH KONSTRUKCIJA 1 Ivan Ignjatović Beograd, 2018. god Impresum Autori: Naslov: Izdavač: Za izdavača: Recenzenti: Dizajn: Tiraž: Štampa: Mesto: Godina izdanja: ISBN: Dr Ivan
ZBIRKA ZADATAKA TEORIJA BETONSKIH KONSTRUKCIJA 1 Ivan Ignjatović Beograd, 2018. god Impresum Autori: Naslov: Izdavač: Za izdavača: Recenzenti: Dizajn: Tiraž: Štampa: Mesto: Godina izdanja: ISBN: Dr Ivan
Microsoft PowerPoint - ME_P1-Uvodno predavanje [Compatibility Mode]
![Microsoft PowerPoint - ME_P1-Uvodno predavanje [Compatibility Mode] Microsoft PowerPoint - ME_P1-Uvodno predavanje [Compatibility Mode]](/thumbs/103/157430298.jpg) MAŠINSKI ELEMENTI dr Miloš Ristić UVOD Mašinski elementi predstavljaju tehničkonaučnu disciplinu. Izučavanjem ove discipline stiču seteorijska i praktična znanja za proračun, izbor i primenu mašinskih
MAŠINSKI ELEMENTI dr Miloš Ristić UVOD Mašinski elementi predstavljaju tehničkonaučnu disciplinu. Izučavanjem ove discipline stiču seteorijska i praktična znanja za proračun, izbor i primenu mašinskih
Slide 1
 Betonske konstrukcije 1 - vežbe 4 - Dijagram interakcije Građevinski fakultet Univerziteta u Beogradu Betonske konstrukcije 1 1 Građevinski fakultet Univerziteta u Beogradu Betonske konstrukcije 1 1 2
Betonske konstrukcije 1 - vežbe 4 - Dijagram interakcije Građevinski fakultet Univerziteta u Beogradu Betonske konstrukcije 1 1 Građevinski fakultet Univerziteta u Beogradu Betonske konstrukcije 1 1 2
Microsoft PowerPoint - predavanje_sile_primena_2013
 Примене Њутнових закона Претпоставке Објекти представљени материјалном тачком занемарите ротацију (за сада) Масе конопаца су занемариве Заинтересовани смо само за силе које делују на објекат можемо да
Примене Њутнових закона Претпоставке Објекти представљени материјалном тачком занемарите ротацију (за сада) Масе конопаца су занемариве Заинтересовани смо само за силе које делују на објекат можемо да
Microsoft PowerPoint - IS_G_predavanja_ [Compatibility Mode]
![Microsoft PowerPoint - IS_G_predavanja_ [Compatibility Mode] Microsoft PowerPoint - IS_G_predavanja_ [Compatibility Mode]](/thumbs/103/157511151.jpg) INŽENJERSKE SIMULACIJE Aleksandar Karač Kancelarija 1111 tel: 44 91 20, lok. 129 akarac@ptf.unze.ba Nermin Redžić Kancelarija 4202 tel: 44 91 20, lok.128 nermin.redzic@ptf.unze.ba www.ptf.unze.ba http://ptf.unze.ba/inzenjerske-simulacije
INŽENJERSKE SIMULACIJE Aleksandar Karač Kancelarija 1111 tel: 44 91 20, lok. 129 akarac@ptf.unze.ba Nermin Redžić Kancelarija 4202 tel: 44 91 20, lok.128 nermin.redzic@ptf.unze.ba www.ptf.unze.ba http://ptf.unze.ba/inzenjerske-simulacije
АНАЛИЗА ПРОБЛЕМА ТЕРМИЧКЕ ДИЛАТАЦИЈЕ L КОМПЕНЗАТОРА ПРЕМА СТАНДАРДУ AD 2000 И ДРУГИМ МЕТОДАМА Милан Травица Иновациони центар Машински факултет Универ
 АНАЛИЗА ПРОБЛЕМА ТЕРМИЧКЕ ДИЛАТАЦИЈЕ L КОМПЕНЗАТОРА ПРЕМА СТАНДАРДУ AD 2000 И ДРУГИМ МЕТОДАМА Милан Травица Иновациони центар Машински факултет Универзитет у Београду Краљице Марије 16, 11000 Београд mtravica@mas.bg.ac.rs
АНАЛИЗА ПРОБЛЕМА ТЕРМИЧКЕ ДИЛАТАЦИЈЕ L КОМПЕНЗАТОРА ПРЕМА СТАНДАРДУ AD 2000 И ДРУГИМ МЕТОДАМА Милан Травица Иновациони центар Машински факултет Универзитет у Београду Краљице Марије 16, 11000 Београд mtravica@mas.bg.ac.rs
God_Rasp_2015_ xls
 ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА, НОВИ САД Датум: 14.09.2016, Страна: 1 I I I 1 13 Грађевински материјали и конструкције I 28.01.2016 09.02.2016 31.03.2016 16.06.2016 04.07.2016 01.09.2016 15.09.2016 26.09.2016
ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА, НОВИ САД Датум: 14.09.2016, Страна: 1 I I I 1 13 Грађевински материјали и конструкције I 28.01.2016 09.02.2016 31.03.2016 16.06.2016 04.07.2016 01.09.2016 15.09.2016 26.09.2016
Slide 1
 BETONSKE KONSTRUKCIJE 2 vježbe, 12.-13.12.2017. 12.-13.12.2017. DATUM SATI TEMATSKA CJELINA 10.- 11.10.2017. 2 17.-18.10.2017. 2 24.-25.10.2017. 2 31.10.- 1.11.2017. uvod ponavljanje poznatih postupaka
BETONSKE KONSTRUKCIJE 2 vježbe, 12.-13.12.2017. 12.-13.12.2017. DATUM SATI TEMATSKA CJELINA 10.- 11.10.2017. 2 17.-18.10.2017. 2 24.-25.10.2017. 2 31.10.- 1.11.2017. uvod ponavljanje poznatih postupaka
Microsoft Word - GI_novo - materijali za ispit
 GEOTEHNIČKO INŽENJERSTVO DIJAGRAMI, TABLICE I FORMULE ZA ISPIT ak.god. 2011/2012 2 1 υi s yi = pb I syi Ei Slika 1. Proračun slijeganja vrha temelja po metodi prema Mayne & Poulos. Slika 2. Proračun nosivosti
GEOTEHNIČKO INŽENJERSTVO DIJAGRAMI, TABLICE I FORMULE ZA ISPIT ak.god. 2011/2012 2 1 υi s yi = pb I syi Ei Slika 1. Proračun slijeganja vrha temelja po metodi prema Mayne & Poulos. Slika 2. Proračun nosivosti
Microsoft Word - MUS ispitna pitanja 2015.doc
 Univerzitet u Novom Sadu Ekonomski fakultet u Subotici Dr. Agneš Slavić, docent Nemanja Berber, asistent Školska 2014/15 godina MENADŽMENT URBANOM SREDINOM Prvi deo: ispitna pitanja 1. PREDMET IZUČAVANJA
Univerzitet u Novom Sadu Ekonomski fakultet u Subotici Dr. Agneš Slavić, docent Nemanja Berber, asistent Školska 2014/15 godina MENADŽMENT URBANOM SREDINOM Prvi deo: ispitna pitanja 1. PREDMET IZUČAVANJA
Microsoft Word Istorija Dinamike Naucnici doc
 Iz Istorije DINAMIKE Ko je dao značajne doprinose da se utemelji naučna oblast pod imenom Dinamika? 1* Odgovarajući na pitanje: Ko je dao značajne doprinose da se utemelji naučna oblast pod imenom Dinamika?
Iz Istorije DINAMIKE Ko je dao značajne doprinose da se utemelji naučna oblast pod imenom Dinamika? 1* Odgovarajući na pitanje: Ko je dao značajne doprinose da se utemelji naučna oblast pod imenom Dinamika?
Stručno usavršavanje
 TOPLINSKI MOSTOVI IZRAČUN PO HRN EN ISO 14683 U organizaciji: TEHNIČKI PROPIS O RACIONALNOJ UPORABI ENERGIJE I TOPLINSKOJ ZAŠTITI U ZGRADAMA (NN 128/15, 70/18, 73/18, 86/18) dalje skraćeno TP Čl. 4. 39.
TOPLINSKI MOSTOVI IZRAČUN PO HRN EN ISO 14683 U organizaciji: TEHNIČKI PROPIS O RACIONALNOJ UPORABI ENERGIJE I TOPLINSKOJ ZAŠTITI U ZGRADAMA (NN 128/15, 70/18, 73/18, 86/18) dalje skraćeno TP Čl. 4. 39.
Microsoft PowerPoint - Opruge kao funkcionalni elementi vezbe2.ppt
 Deformacija opruge: 8FD Gd n f m 4 8Fwn Gd 1 Broj zavojaka opruge Kod pritisnih opruga sa velikim brojem promena opterećenja preporučuje se da se broj zavojaka završava na 0.5, npr..5, 4.5, 5.5... Ukupan
Deformacija opruge: 8FD Gd n f m 4 8Fwn Gd 1 Broj zavojaka opruge Kod pritisnih opruga sa velikim brojem promena opterećenja preporučuje se da se broj zavojaka završava na 0.5, npr..5, 4.5, 5.5... Ukupan
Субструктура гредних мостова
 Субструктура гредних мостова Стубови моста 2 Крајњи стубови - опорци Средњи стубови Крајњи стуб опорац 3 Изглед 4 Пратећи елементи крајњих стубова УЛОГА: Помажу при повезивању трупа пута на насипу и коловоза
Субструктура гредних мостова Стубови моста 2 Крајњи стубови - опорци Средњи стубови Крајњи стуб опорац 3 Изглед 4 Пратећи елементи крајњих стубова УЛОГА: Помажу при повезивању трупа пута на насипу и коловоза
_cas 8 temelji i gredni sistemi
 Одсек ПЖA Мостови Предавање 8 29. Март 2019. Типови темеља Плитко фундирање Дубоко фундирање Шипови Бунари Кесони Извођење на сувом и извођење у воденој препреци др Снежана Машовић Школска 2018/19 2 Плитко
Одсек ПЖA Мостови Предавање 8 29. Март 2019. Типови темеља Плитко фундирање Дубоко фундирање Шипови Бунари Кесони Извођење на сувом и извођење у воденој препреци др Снежана Машовић Школска 2018/19 2 Плитко
Uvod u statistiku
 Uvod u statistiku Osnovni pojmovi Statistika nauka o podacima Uključuje prikupljanje, klasifikaciju, prikaz, obradu i interpretaciju podataka Staistička jedinica objekat kome se mjeri neko svojstvo. Svi
Uvod u statistiku Osnovni pojmovi Statistika nauka o podacima Uključuje prikupljanje, klasifikaciju, prikaz, obradu i interpretaciju podataka Staistička jedinica objekat kome se mjeri neko svojstvo. Svi
ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ
 Универзитет у Београду, Електротехнички факултет, Катедра за енергетске претвараче и погоне ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ (3Е3ЕНТ) Јул 9. Трофазни уљни енергетски трансформатор са номиналним подацима: 4 V,
Универзитет у Београду, Електротехнички факултет, Катедра за енергетске претвараче и погоне ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ (3Е3ЕНТ) Јул 9. Трофазни уљни енергетски трансформатор са номиналним подацима: 4 V,
Primjena neodredenog integrala u inženjerstvu Matematika 2 Erna Begović Kovač, Literatura: I. Gusić, Lekcije iz Matematike 2
 Primjena neodredenog integrala u inženjerstvu Matematika 2 Erna Begović Kovač, 2019. Literatura: I. Gusić, Lekcije iz Matematike 2 http://matematika.fkit.hr Uvod Ako su dvije veličine x i y povezane relacijom
Primjena neodredenog integrala u inženjerstvu Matematika 2 Erna Begović Kovač, 2019. Literatura: I. Gusić, Lekcije iz Matematike 2 http://matematika.fkit.hr Uvod Ako su dvije veličine x i y povezane relacijom
NASLOV RADA (12 pt, bold, Times New Roman)
 9 th International Scientific Conference on Production Engineering DEVELOPMENT AND MODERNIZATION OF PRODUCTION PRIMJENA METODE KONAČNIH ELEMENATA U ANALIZI OPTEREĆENJA PLASTIČNE PREKLOPIVE AMBALAŽE Damir
9 th International Scientific Conference on Production Engineering DEVELOPMENT AND MODERNIZATION OF PRODUCTION PRIMJENA METODE KONAČNIH ELEMENATA U ANALIZI OPTEREĆENJA PLASTIČNE PREKLOPIVE AMBALAŽE Damir
Оsnovni principi u projektovanju mostova
 КОЛОВОЗНА КОНСТРУКЦИЈА БЕТОНСКИХ МОСТОВА 1 Типови попречног пресека коловоне конструкције Избор типа поречног пресека зависи од : Распона коловозне конструкцие Расположиве висине Начина извођења Постоје:
КОЛОВОЗНА КОНСТРУКЦИЈА БЕТОНСКИХ МОСТОВА 1 Типови попречног пресека коловоне конструкције Избор типа поречног пресека зависи од : Распона коловозне конструкцие Расположиве висине Начина извођења Постоје:
Toplinska i električna vodljivost metala
 Električna vodljivost metala Cilj vježbe Određivanje koeficijenta električne vodljivosti bakra i aluminija U-I metodom. Teorijski dio Eksperimentalno je utvrđeno da otpor ne-ohmskog vodiča raste s porastom
Električna vodljivost metala Cilj vježbe Određivanje koeficijenta električne vodljivosti bakra i aluminija U-I metodom. Teorijski dio Eksperimentalno je utvrđeno da otpor ne-ohmskog vodiča raste s porastom
Slide 1
 Анализа електроенергетских система -Прорачун кратких спојева- Кратак спој представља поремећено стање мреже, односно поремећено стање система. За време трајања кратког споја напони и струје се мењају са
Анализа електроенергетских система -Прорачун кратких спојева- Кратак спој представља поремећено стање мреже, односно поремећено стање система. За време трајања кратког споја напони и струје се мењају са
Građevinski Fakultet Univerziteta u Beogradu
 Грађевински факултет Универзитета у Београду МОСТОВИ Упутство за прегледање мостова и прорачун рејтинга моста Вежбе 6 1 Марковљев ланац Моделирање пропадања конструкције Прелазне вероватноће р 11 вероватноћа
Грађевински факултет Универзитета у Београду МОСТОВИ Упутство за прегледање мостова и прорачун рејтинга моста Вежбе 6 1 Марковљев ланац Моделирање пропадања конструкције Прелазне вероватноће р 11 вероватноћа
Microsoft Word - CAD sistemi
 U opštem slučaju, se mogu podeliti na 2D i 3D. 2D Prvo pojavljivanje 2D CAD sistema se dogodilo pre više od 30 godina. Do tada su inženjeri koristili table za crtanje (kulman), a zajednički jezik komuniciranja
U opštem slučaju, se mogu podeliti na 2D i 3D. 2D Prvo pojavljivanje 2D CAD sistema se dogodilo pre više od 30 godina. Do tada su inženjeri koristili table za crtanje (kulman), a zajednički jezik komuniciranja
ma??? - Primer 6 Proracun spregnute veze
 Primer 6 Proračun spregnute veze Odrediti proračunski moment nosivosti spregnute veze grede i stuba prikazane na skici. Stub je izrađen od vrućevaljanog profila HEA400, a greda od IPE500. Veza je ostvarena
Primer 6 Proračun spregnute veze Odrediti proračunski moment nosivosti spregnute veze grede i stuba prikazane na skici. Stub je izrađen od vrućevaljanog profila HEA400, a greda od IPE500. Veza je ostvarena
?? ????????? ?????????? ?????? ?? ????????? ??????? ???????? ?? ??????? ??????:
 РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 003 АСИНХРОНЕ МАШИНЕ Трофазни асинхрони мотор са намотаним ротором има податке: 380V 10A cos ϕ 08 Y 50Hz p отпор статора R s Ω Мотор је испитан
РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 003 АСИНХРОНЕ МАШИНЕ Трофазни асинхрони мотор са намотаним ротором има податке: 380V 10A cos ϕ 08 Y 50Hz p отпор статора R s Ω Мотор је испитан
I година Назив предмета I термин Вријеме II термин Вријеме Сала Математика : :00 све Основи електротехнике
 I година Математика 1 2225 20.06.2019. 9:00 04.07.2019. 9:00 све Основи електротехнике 1 2226 17.06.2019. 9:00 01.07.2019. 13:00 све Програмирање 1 2227 21.06.2019. 9:00 05.07.2019. 9:00 све Основи рачунарске
I година Математика 1 2225 20.06.2019. 9:00 04.07.2019. 9:00 све Основи електротехнике 1 2226 17.06.2019. 9:00 01.07.2019. 13:00 све Програмирање 1 2227 21.06.2019. 9:00 05.07.2019. 9:00 све Основи рачунарске
I година Назив предмета I термин Вријеме II термин Вријеме Сала Математика : :00 све Основи електротехнике
 I година Математика 1 2225 05.09.2019. 9:00 19.09.2019. 9:00 све Основи електротехнике 1 2226 02.09.2019. 9:00 16.09.2019. 9:00 све Програмирање 1 2227 06.09.2019. 9:00 20.09.2019. 9:00 све Основи рачунарске
I година Математика 1 2225 05.09.2019. 9:00 19.09.2019. 9:00 све Основи електротехнике 1 2226 02.09.2019. 9:00 16.09.2019. 9:00 све Програмирање 1 2227 06.09.2019. 9:00 20.09.2019. 9:00 све Основи рачунарске
I година Назив предмета I термин Вријеме II термин Вријеме Сала Математика : :00 све Основи електротехнике
 I година Математика 1 2225 07.02.2019. 9:00 21.02.2019. 9:00 све Основи електротехнике 1 2226 04.02.2019. 9:00 18.02.2019. 9:00 све Програмирање 1 2227 08.02.2019. 9:00 22.02.2019. 9:00 све Основи рачунарске
I година Математика 1 2225 07.02.2019. 9:00 21.02.2019. 9:00 све Основи електротехнике 1 2226 04.02.2019. 9:00 18.02.2019. 9:00 све Програмирање 1 2227 08.02.2019. 9:00 22.02.2019. 9:00 све Основи рачунарске
I година Назив предмета I термин Вријеме Сала Математика :00 све Основи електротехнике :00 све Програмирање
 I година Математика 1 2225 03.10.2019. 15:00 све Основи електротехнике 1 2226 30.09.2019. 15:00 све Програмирање 1 2227 04.10.2019. 15:00 све Основи рачунарске технике 2228 01.10.2019. 15:00 све Социологија
I година Математика 1 2225 03.10.2019. 15:00 све Основи електротехнике 1 2226 30.09.2019. 15:00 све Програмирање 1 2227 04.10.2019. 15:00 све Основи рачунарске технике 2228 01.10.2019. 15:00 све Социологија
Microsoft Word - ETH2_EM_Amperov i generalisani Amperov zakon - za sajt
 Полупречник унутрашњег проводника коаксијалног кабла је Спољашњи проводник је коначне дебљине унутрашњег полупречника и спољашњег Проводници кабла су начињени од бакра Кроз кабл протиче стална једносмерна
Полупречник унутрашњег проводника коаксијалног кабла је Спољашњи проводник је коначне дебљине унутрашњег полупречника и спољашњег Проводници кабла су начињени од бакра Кроз кабл протиче стална једносмерна
Microsoft PowerPoint - Teorija kretanja vozila-predavanje 3.1.ppt
 ТЕОРИЈА КРЕТАЊА ВОЗИЛА Предавање. гусенична возила, површински притисак ослањања, гусеница на подлогу ослањања G=mg p p гусеница на подлогу ослањања G=mg средњи стварни p тврда подлога средњи стварни p
ТЕОРИЈА КРЕТАЊА ВОЗИЛА Предавање. гусенична возила, површински притисак ослањања, гусеница на подлогу ослањања G=mg p p гусеница на подлогу ослањања G=mg средњи стварни p тврда подлога средњи стварни p
ka prof-miomir-mijic-etf-beograd
 NOVA UREDBA O AKUSTIČKOM KOMFORU U ZGRADAMA (u pripremi) Istorijat normativa koji regulišu akustički komfor u zgradama Za sada su samo Slovenija i Crna gora napravile otklon od starog JUS-a U Srbiji je
NOVA UREDBA O AKUSTIČKOM KOMFORU U ZGRADAMA (u pripremi) Istorijat normativa koji regulišu akustički komfor u zgradama Za sada su samo Slovenija i Crna gora napravile otklon od starog JUS-a U Srbiji je
Ivan GLIŠOVIĆ Boško STEVANOVIĆ Marija TODOROVIĆ PRORAČUN DRVENIH KONSTRUKCIJA PREMA EVROKODU 5 Građevinski fakultet Univerziteta u Beogradu Akademska
 Ivan GLIŠOVIĆ Boško STEVANOVIĆ Marija TODOROVIĆ PRORAČUN DRVENIH KONSTRUKCIJA PREMA EVROKODU 5 Građevinski fakultet Univerziteta u Beogradu Akademska misao, Beograd Dr Ivan Glišović, dipl.inž.građ., docent
Ivan GLIŠOVIĆ Boško STEVANOVIĆ Marija TODOROVIĆ PRORAČUN DRVENIH KONSTRUKCIJA PREMA EVROKODU 5 Građevinski fakultet Univerziteta u Beogradu Akademska misao, Beograd Dr Ivan Glišović, dipl.inž.građ., docent
PowerPoint Presentation
 МОБИЛНЕ МАШИНЕ II предавање 4.2 \ ослоно-кретни механизми на точковима, кинематика и динамика точка Кинематика точка обимна брзини точка: = t транслаторна брзина точка: = t Услов котрљања точка без проклизавања:
МОБИЛНЕ МАШИНЕ II предавање 4.2 \ ослоно-кретни механизми на точковима, кинематика и динамика точка Кинематика точка обимна брзини точка: = t транслаторна брзина точка: = t Услов котрљања точка без проклизавања:
Slide 1
 Грађевински факултет Универзитета у Београду МОСТОВИ Субструктура моста Вежбе 4 Програм предмета Датум бч. Предавања бч. Вежбе 1 22.02. 4 Уводно предавање - 2 01.03. 3 Дефиниције, системи, распони и материјали
Грађевински факултет Универзитета у Београду МОСТОВИ Субструктура моста Вежбе 4 Програм предмета Датум бч. Предавања бч. Вежбе 1 22.02. 4 Уводно предавање - 2 01.03. 3 Дефиниције, системи, распони и материјали
Републички педагошки завод Бања Лука Стручни савјетник за машинску групу предмета и практичну наставу Датум: године Тема: Елементи и начин
 Републички педагошки завод Бања Лука Стручни савјетник за машинску групу предмета и практичну наставу Датум:.06.2009. године Тема: Елементи и начин вредновања графичког рада из раванских носачи 1 Увод:
Републички педагошки завод Бања Лука Стручни савјетник за машинску групу предмета и практичну наставу Датум:.06.2009. године Тема: Елементи и начин вредновања графичког рада из раванских носачи 1 Увод:
Microsoft Word - Proracun.doc
 PRORAČUN KOJI SE ODNOSI NA POČETNO GAŠENJE POŽARA R. Br Požarni sektor Naziv objekta Površina objekta (m 2 ) Požarno opterećenje (MJ/m 2 ) Kategorizacija požarnog opterećenja (GJ/m 2 ) Potreban broj aparata
PRORAČUN KOJI SE ODNOSI NA POČETNO GAŠENJE POŽARA R. Br Požarni sektor Naziv objekta Površina objekta (m 2 ) Požarno opterećenje (MJ/m 2 ) Kategorizacija požarnog opterećenja (GJ/m 2 ) Potreban broj aparata
Зборник радова 6. Међународне конференције о настави физике у средњим школама, Алексинац, март Нелинеарно еластично клатно Милан С. Коваче
 Нелинеарно еластично клатно Милан С. Ковачевић 1, Мирослав Јовановић 2 1 Природно-математички факултет, Крагујевац, Србија 2 Гимназија Јосиф Панчић Бајина Башта, Србија Апстракт. У овом раду је описан
Нелинеарно еластично клатно Милан С. Ковачевић 1, Мирослав Јовановић 2 1 Природно-математички факултет, Крагујевац, Србија 2 Гимназија Јосиф Панчић Бајина Башта, Србија Апстракт. У овом раду је описан
Univerzitet u Beogradu Elektrotehnički fakultet Katedra za energetske pretvarače i pogone ISPIT IZ SINHRONIH MAŠINA (13E013SIM) 1. Poznati su podaci o
 Univerzitet u Beogradu Elektrotehnički akultet Katedra za energetske pretvarače i pogone ISPIT IZ SINHRONIH MAŠINA (13E013SIM) 1. Poznati su podaci o namotaju statora sinhronog motora sa stalnim magnetima
Univerzitet u Beogradu Elektrotehnički akultet Katedra za energetske pretvarače i pogone ISPIT IZ SINHRONIH MAŠINA (13E013SIM) 1. Poznati su podaci o namotaju statora sinhronog motora sa stalnim magnetima
Microsoft Word - REGIONALNA EKONOMIJA EVROPSKE UNIJE_Ispit.doc
 UNIVERZITET U NOVOM SADU EKONOMSKI FAKULTET U SUBOTICI SOFIJA ADŽIĆ REGIONALNA EKONOMIJA EVROPSKE UNIJE ISPITNA PITANJA Školska 2012/2013 godina Verzija 2.0 Subotica, septembar 2012. REGIONALNA EKONOMIJA
UNIVERZITET U NOVOM SADU EKONOMSKI FAKULTET U SUBOTICI SOFIJA ADŽIĆ REGIONALNA EKONOMIJA EVROPSKE UNIJE ISPITNA PITANJA Školska 2012/2013 godina Verzija 2.0 Subotica, septembar 2012. REGIONALNA EKONOMIJA
Mere slicnosti
 Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
ФАКУЛТЕТ ОРГАНИЗАЦИОНИХ НАУКА
 Питања за усмени део испита из Математике 3 I. ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ 1. Појам диференцијалне једначине. Пикарова теорема. - Написати општи и нормални облик диференцијалне једначине првог реда. - Дефинисати:
Питања за усмени део испита из Математике 3 I. ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ 1. Појам диференцијалне једначине. Пикарова теорема. - Написати општи и нормални облик диференцијалне једначине првог реда. - Дефинисати:
mfb_april_2018_res.dvi
 Универзитет у Београду Машински факултет Катедра за механику флуида МЕХАНИКА ФЛУИДА Б Писмени део испита Име и презиме:... Броj индекса:... Напомене: Испит траjе 80 минута. Коришћење литературе ниjе дозвољено!
Универзитет у Београду Машински факултет Катедра за механику флуида МЕХАНИКА ФЛУИДА Б Писмени део испита Име и презиме:... Броj индекса:... Напомене: Испит траjе 80 минута. Коришћење литературе ниjе дозвољено!
Classroom Expectations
 АТ-8: Терминирање производно-технолошких ентитета Проф. др Зоран Миљковић Садржај Пројектовање флексибилних ; Математички модел за оптимизацију флексибилних ; Генетички алгоритми у оптимизацији флексибилних
АТ-8: Терминирање производно-технолошких ентитета Проф. др Зоран Миљковић Садржај Пројектовање флексибилних ; Математички модел за оптимизацију флексибилних ; Генетички алгоритми у оптимизацији флексибилних
Microsoft PowerPoint - fizika 4-rad,snaga,energija2014
 ФИЗИКА Понедељак, 3. Новембар, 2014 1. Рад 2. Кинетичка енергија 3. Потенцијална енергија 1. Конзервативне силе и потенцијална енергија 2. Неконзервативне силе. Отворенисистеми 4. Закон одржања енергије
ФИЗИКА Понедељак, 3. Новембар, 2014 1. Рад 2. Кинетичка енергија 3. Потенцијална енергија 1. Конзервативне силе и потенцијална енергија 2. Неконзервативне силе. Отворенисистеми 4. Закон одржања енергије
Microsoft PowerPoint - fizika2-kinematika2012
 ФИЗИКА 1. Понедељак, 8. октобар, 1. Кинематика тачке у једној димензији Кинематикакретањаудведимензије 1 Кинематика кретање свејеустањукретања кретање промена положаја тела (уодносу на друга тела) три
ФИЗИКА 1. Понедељак, 8. октобар, 1. Кинематика тачке у једној димензији Кинематикакретањаудведимензије 1 Кинематика кретање свејеустањукретања кретање промена положаја тела (уодносу на друга тела) три
6. TEHNIČKE MJERE SIGURNOSTI U IZVEDBI ELEKTROENERGETSKIH VODOVA
 SIGURNOST U PRIMJENI ELEKTRIČNE ENERGIJE 6. TEHNIČKE MJERE SIGURNOSTI U IZVEDBI ELEKTROENERGETSKIH VODOVA Izv.prof. dr.sc. Vitomir Komen, dipl.ing.el. 1/14 SADRŽAJ: 6.1 Sigurnosni razmaci i sigurnosne
SIGURNOST U PRIMJENI ELEKTRIČNE ENERGIJE 6. TEHNIČKE MJERE SIGURNOSTI U IZVEDBI ELEKTROENERGETSKIH VODOVA Izv.prof. dr.sc. Vitomir Komen, dipl.ing.el. 1/14 SADRŽAJ: 6.1 Sigurnosni razmaci i sigurnosne
#придружи се најбољима Ми улажемо у будућност. Будућност си ти. Постани део успешне Алфа БК породице! О Р Г А Н И З А Ц И Ј А, Т Е Х Н О Л О Г И Ј А Г
 #придружи се најбољима Ми улажемо у будућност. Будућност си ти. Постани део успешне Алфа БК породице! О Р Г А Н И З А Ц И Ј А, Т Е Х Н О Л О Г И Ј А Г Р А Ђ Е Њ А И М Е Н А Џ М Е Н Т У Г Р А Ђ Е В И Н
#придружи се најбољима Ми улажемо у будућност. Будућност си ти. Постани део успешне Алфа БК породице! О Р Г А Н И З А Ц И Ј А, Т Е Х Н О Л О Г И Ј А Г Р А Ђ Е Њ А И М Е Н А Џ М Е Н Т У Г Р А Ђ Е В И Н
Microsoft Word - Elektrijada_V2_2014_final.doc
 I област. У колу сталне струје са слике када је и = V, амперметар показује I =. Одредити показивање амперметра I када је = 3V и = 4,5V. Решење: а) I = ) I =,5 c) I =,5 d) I = 7,5 3 3 Слика. I област. Дата
I област. У колу сталне струје са слике када је и = V, амперметар показује I =. Одредити показивање амперметра I када је = 3V и = 4,5V. Решење: а) I = ) I =,5 c) I =,5 d) I = 7,5 3 3 Слика. I област. Дата
untitled
 С А Д Р Ж А Ј Предговор...1 I II ОСНОВНИ ПОЈМОВИ И ДЕФИНИЦИЈЕ...3 1. Предмет и метод термодинамике... 3 2. Термодинамички систем... 4 3. Величине (параметри) стања... 6 3.1. Специфична запремина и густина...
С А Д Р Ж А Ј Предговор...1 I II ОСНОВНИ ПОЈМОВИ И ДЕФИНИЦИЈЕ...3 1. Предмет и метод термодинамике... 3 2. Термодинамички систем... 4 3. Величине (параметри) стања... 6 3.1. Специфична запремина и густина...
Рапоред полагања испита школске године 2018/19. Ниво студија Основне академске студије Акредитација 2014 Машинско инжењерство Сатница испита Студијски
 Рапоред полагања испита школске године 2018/19. Ниво студија Основне академске студије Акредитација 2014 Машинско инжењерство Сатница испита Студијски програм 9:00 КОД Н А З И В П Р Е Д М Е Т А ЈАН МАР
Рапоред полагања испита школске године 2018/19. Ниво студија Основне академске студије Акредитација 2014 Машинско инжењерство Сатница испита Студијски програм 9:00 КОД Н А З И В П Р Е Д М Е Т А ЈАН МАР
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић
 Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Драган Пејић, Бојан Вујичић, Небојша Пјевалица,
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Драган Пејић, Бојан Вујичић, Небојша Пјевалица,
Факултет педагошких наука Универзитета у Крагујевцу, Јагодина Весна Трифуновић ПРАКТИКУМ ИЗ СОЦИОЛОГИЈЕ ОБРАЗОВАЊА Јагодина 2018
 Факултет педагошких наука Универзитета у Крагујевцу, Јагодина Весна Трифуновић ПРАКТИКУМ ИЗ СОЦИОЛОГИЈЕ ОБРАЗОВАЊА Јагодина 2018 Издавач Факултет педагошких наука Универзитета у Крагујевцу Милана Мијалковића
Факултет педагошких наука Универзитета у Крагујевцу, Јагодина Весна Трифуновић ПРАКТИКУМ ИЗ СОЦИОЛОГИЈЕ ОБРАЗОВАЊА Јагодина 2018 Издавач Факултет педагошких наука Универзитета у Крагујевцу Милана Мијалковића
JUN.xlsx
 1 Математика 1 (П) 17.06. у 13:00 Амф. 2 Хемија (П+У) 14.06. у 09:00 Амф. 3 Рачунарска техника (П+У) 20.06. у 13:00 Амф. 4 Основи система заштите (У) 18.06. у 13:00 201 5 Социологија (У) 10.06. у 09:00
1 Математика 1 (П) 17.06. у 13:00 Амф. 2 Хемија (П+У) 14.06. у 09:00 Амф. 3 Рачунарска техника (П+У) 20.06. у 13:00 Амф. 4 Основи система заштите (У) 18.06. у 13:00 201 5 Социологија (У) 10.06. у 09:00
ТЕСТ ИЗ ФИЗИКЕ ИМЕ И ПРЕЗИМЕ 1. У основне величине у физици, по Међународном систему јединица, спадају и следеће три величине : а) маса, температура,
 ТЕСТ ИЗ ФИЗИКЕ ИМЕ И ПРЕЗИМЕ 1. У основне величине у физици, по Међународном систему јединица, спадају и следеће три величине : а) маса, температура, електрични отпор б) сила, запремина, дужина г) маса,
ТЕСТ ИЗ ФИЗИКЕ ИМЕ И ПРЕЗИМЕ 1. У основне величине у физици, по Међународном систему јединица, спадају и следеће три величине : а) маса, температура, електрични отпор б) сила, запремина, дужина г) маса,
PowerPoint Presentation
 Nedjelja 6 - Lekcija Projiciranje Postupci projiciranja Projiciranje je postupak prikazivanja oblika nekog, u opštem slučaju trodimenzionalnog, predmeta dvodimenzionalnim crtežom. Postupci projiciranja
Nedjelja 6 - Lekcija Projiciranje Postupci projiciranja Projiciranje je postupak prikazivanja oblika nekog, u opštem slučaju trodimenzionalnog, predmeta dvodimenzionalnim crtežom. Postupci projiciranja
Ефекти реолошких карактеристика бетона
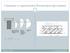 Смицање у спрегнутим бетонским пресецима 1 Смицање у споју спрегнутих пресека 2 Смицање у споју композитног бетонског пресека 3 Смицање и попречно савијање 4 Интеракција торзије и трансверзалних сила 5
Смицање у спрегнутим бетонским пресецима 1 Смицање у споју спрегнутих пресека 2 Смицање у споју композитног бетонског пресека 3 Смицање и попречно савијање 4 Интеракција торзије и трансверзалних сила 5
Geometrija molekula
 Geometrija molekula Oblik molekula predstavlja trodimenzionalni raspored atoma u okviru molekula. Geometrija molekula je veoma važan faktor koji određuje fizička i hemijska svojstva nekog jedinjenja, kao
Geometrija molekula Oblik molekula predstavlja trodimenzionalni raspored atoma u okviru molekula. Geometrija molekula je veoma važan faktor koji određuje fizička i hemijska svojstva nekog jedinjenja, kao
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аут
 Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Иван Жупунски, Небојша Пјевалица, Марјан Урекар,
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Иван Жупунски, Небојша Пјевалица, Марјан Урекар,
Slide 1
 EVROPSKA UNIJA VLADA RUMUNIJE VLADA REPUBLIKE SRBIJE Strukturni fondovi 2007-2013 Logo projekta / Logo Vodećeg partnera ЕВРОПСКА ТЕХНОЛОШКА ПЛАТФОРМА ЗА БУДУЋНОСТ ТЕКСТИЛА И ОДЕЋЕ ВИЗИЈА ЗА 2020 Будући
EVROPSKA UNIJA VLADA RUMUNIJE VLADA REPUBLIKE SRBIJE Strukturni fondovi 2007-2013 Logo projekta / Logo Vodećeg partnera ЕВРОПСКА ТЕХНОЛОШКА ПЛАТФОРМА ЗА БУДУЋНОСТ ТЕКСТИЛА И ОДЕЋЕ ВИЗИЈА ЗА 2020 Будући
Elektrotehnički fakultet Univerziteta u Beogradu Relejna zaštita laboratorijske vežbe Vežba 4: ISPITIVANJE STATIČKE GENERATORSKE ZAŠTITE Cilj vežbe je
 Vežba 4: ISPITIVANJE STATIČKE GENERATORSKE ZAŠTITE Cilj vežbe je ispitivanje sledećih zaštitnih releja: (1) zemljospojnog za zaštitu statora generatora (RUWA 117 E), (2) podnaponskog releja (RUVA 116 E),
Vežba 4: ISPITIVANJE STATIČKE GENERATORSKE ZAŠTITE Cilj vežbe je ispitivanje sledećih zaštitnih releja: (1) zemljospojnog za zaštitu statora generatora (RUWA 117 E), (2) podnaponskog releja (RUVA 116 E),
Шумска транспортна средства - испитна питања
 I ШУМСКИ ПУТЕВИ (38 питања) 1. Како се врши рекогносцирање терена, утврђивање чворних тачака и просечног нагиба између чворних тачака? 2. Какав значај имају шумска транспортна средстава и који је степен
I ШУМСКИ ПУТЕВИ (38 питања) 1. Како се врши рекогносцирање терена, утврђивање чворних тачака и просечног нагиба између чворних тачака? 2. Какав значај имају шумска транспортна средстава и који је степен
Microsoft PowerPoint - Teorija kretanja vozila-predavanje 4.1.ppt
 ТЕОРИЈА КРЕТАЊА ВОЗИЛА Предавање 4.1 гусенична возила, отпори кретања, Код дефинисања параметара функција кретања возила на гусеницама разматрају се следећи случајеви кретања: а) праволиниjско кретање
ТЕОРИЈА КРЕТАЊА ВОЗИЛА Предавање 4.1 гусенична возила, отпори кретања, Код дефинисања параметара функција кретања возила на гусеницама разматрају се следећи случајеви кретања: а) праволиниjско кретање
Microsoft Word - Upis kandidata ??S sep
 УПИС КАНДИДАТА Упис кандидата обавиће се у соби 05, у терминима утврђеним терминским планом. Кандидати који стекну право уписа подносе: - Диплому, или уверење о завршеном првом степену или уверење о положеним
УПИС КАНДИДАТА Упис кандидата обавиће се у соби 05, у терминима утврђеним терминским планом. Кандидати који стекну право уписа подносе: - Диплому, или уверење о завршеном првом степену или уверење о положеним
Paper Title (use style: paper title)
 Статистичка анализа коришћења електричне енергије која за последицу има примену повољнијег тарифног става Аутор: Марко Пантовић Факултет техничких наука, Чачак ИАС Техника и информатика, 08/09 e-mal адреса:
Статистичка анализа коришћења електричне енергије која за последицу има примену повољнијег тарифног става Аутор: Марко Пантовић Факултет техничких наука, Чачак ИАС Техника и информатика, 08/09 e-mal адреса:
Microsoft PowerPoint - DS-1-16 [Compatibility Mode]
![Microsoft PowerPoint - DS-1-16 [Compatibility Mode] Microsoft PowerPoint - DS-1-16 [Compatibility Mode]](/thumbs/102/155207709.jpg) Ekonometrija 1-D Analiza vremenskih serija Predavač: Zorica Mladenović, zorima@eunet.rs, http://avs.ekof.bg.ac.rs kabinet: 414 1 Struktura predmeta Izučavaju se dve oblasti: Analiza vremenskih serija Analiza
Ekonometrija 1-D Analiza vremenskih serija Predavač: Zorica Mladenović, zorima@eunet.rs, http://avs.ekof.bg.ac.rs kabinet: 414 1 Struktura predmeta Izučavaju se dve oblasti: Analiza vremenskih serija Analiza
