UNIVERZITET U NOVOM SADU
|
|
|
- Ивица Веселиновић
- пре 5 година
- Прикази:
Транскрипт
1 Dr Božo Ilić - Skripta I deo - PRIMENJENE METODE MODELOVANJA RIZIKA / PRIMENJENE METODE MODELOVANJA EKSPERIMENTA Visoka tehnička škola strukovnih studija u Novom Sadu,
2 SADRŽAJ SADRŽAJ ISTRAŽIVANJA Faze istraživačkog rada Izbor teme Proučavanje problematike Definisanje problema i postavljanje hipoteze Planiranje i modelovanje eksperimenta Mere sigurnosti prilikom izvođenja eksperimenta Organizacija rezultata i analiza podataka Prikazivanje rezultata Metode istraživanja Empirijska metoda Metoda posmatranja EKSPERIMENTALNA ISTRAŽIVANJA ISTRAŽIVANJA METODOM MODELOVANJA Pojam modelovanje Ciljevi modelovanja Primeri upotrebe modelovanja Podele modela MATEMATIČKO MODELOVANJE Empirijski modeli Prednosti empirijskih modela Nedostaci empirijskih modela Primeri upotrebe empirijskih modela Primer eksperimentalne identifikacije sistema Teorija sličnosti Dimenziona analiza Empirijske korelacije Korelacije linearna i nelinearna regresija Eksperimentalna validacija modela Deterministički (fundamentalni) modeli Prednosti determinističkih (fundamentalnih) modela Nedostaci determinističkih modela Primeri upotrebe determinističkih (fundamentalnih) modela Nivoi matematičkog opisa sistema i procesa Populacioni modeli Stohastički modeli Primena Monte Karlo metode u modelovanju stohastičkih procesa STATISTIČКA ISTRAŽIVANJA Primena računara u statističkoj analizi
3 5.2. Statistički skup Statističko obeležje Statistički uzorak, reprezentativni uzorak i parametri skupa Prosta korelaciona i regresiona analiza Funkcionalna i stohastička veza Razlika između regresione i korelacione analize Dijagram raspršenosti TEORIJA VEROVATNOĆE Klasična definicija verovatnoće Statistička definicija verovatnoće RAČUNARSKO MODELOVANJE I SIMULACIJA PROCESA Primena softverskog paketa MATLAB u računarskom modelovanju i simulaciji procesa EKOLOŠKO MODELOVANJE Faze (koraci) izrade ekološkog modela Definisanje (identifikacija) problema koga korisnik modela želi da reši korišćenjem tog modela Upoznavanje realnog sistema koji se istražuje (proučava) Izrada konceptualnog modela Postavljanje (usvajanje) pretpostavki modela Izrada (formiranje) matematičkog modela, tj. formiranje jednačina koje na adekvatan način opisuju ponašanje realnog sistema Izrada računarskog modela Verifikacija računarskog modela (testiranje programa) Validacija (vrednovanje) modela realnog sistema Praktična primena (implementacija) modela RIZIK Pojam rizik Procena rizika Kvantitativne metode procene rizika Kvalitativne metode procene rizika Identifikacija opasnosti Modelovanje sistema za kvantitativnu procenu (analizu) rizika Neodređenost Merenje neodređenosti Teorija verovatnoće Rangiranje scenarija rizika Metode procene ekološkog rizika LITERATURA
4 1. ISTRAŽIVANJA Čovek je kroz istoriju nastojao da više sazna o stvarnosti koja ga okružuje, što ga je teralo da stiče različita znanja o pojavama u prirodi i društvu. Metodološko sticanje znanja jeste nauka. Nauka predstavlja skup svih sistematizovanih stečenih znanja (zakona, zakonitosti, teorija itd.) o pojavama u prirodi i društvu do kojih se došlo primenom objektivnih naučnih metoda. Osnovni cilj nauke jeste otkrivanje istine, odnosno utvrđivanje zakona i zakonitosti o pojavama u prirodi i društvu. Nauka se bavi proširivanjem i produbljivanjem saznanja o pojavama (fenomenima) u prirodi i društvu iz prošlosti i sadašnjosti radi prognoziranja i predviđanja ponašanja tih pojava u budućnosti. S obzirom na to koje metode koriste, postoje: neeksperimentalne nauke, kod njih se rezultati istraživanja uglavnom zasnivaju na teoriji i eksperimentalne nauke, kod njih se rezultati istraživanja uglavnom zasnivaju eksperimentima. S obzirom na to da li koriste opšta ili specifična znanja, postoje: deduktivne nauke, koje pored opštih koriste i specifična znanja i induktivne nauke, koje uglavnom koriste opšta znanja. Istraživanja nastaju: iz čovekove radoznalosti, odnosno iz čovekove potrebe da sazna više o stvarnosti koja ga okružuje, i iz čovekove potrebe za progresom, odnosno iz čovekove potrebe za poboljšanjem uslova života i rada. Istraživanja uvek ne doprinose progresu, postoje primeri zloupotrebe istraživanja., Osnovna uloga istraživanja je: verifikacija (provera) postojećih saznanja, proširivanje postojećih saznanja i otkrivanje novih saznanja (zakona, zakonitosti, teorija i sl.). Istraživanja mogu biti: teorijska, zasnivaju se na teoriji i empirijska, zasnivaju se na eksperimentima S obzirom na funkciju istraživanja mogu biti: Fundamentalna (neusmerena, slobodna, bazična) istraživanja, predstavljaju teorijski ili eksperimentalni rad koji je usmeren na proširivanje opšteg fonda znanja a ne na rešavanje praktičnih problema. Primenjena (usmerena, strateška, aplikativna, operativna) istraživanja, predstavljaju teorijski ili eksperimentalni rad koji je usmeren na rešavanje praktičnih problema, a na osnovu rezultata fundamentalnih istraživanja. 3
5 Razvojna istraživanja, predstavljaju teorijski i eksperimentalni rad usmeren na poboljšanje tehnoloških postupaka, izradu novih prototipova proizvoda i sl., a na osnovu rezultata fundamentalnih i primenjenih istraživanja. Razlika između fundamentalnih i primenjenih istraživanja je u tome što su fundamentalna istraživanja usmerena na proširivanje opšteg fonda znanja, a ne na rešavanje praktičnih problema (nemaju praktičnu primenu) kao što su primenjena istraživanja. Nauka istraživački rad deli na naučni i stručni da bi otklonila problem pojave rezultata istraživanja vrlo interesantnih i upotrebljivih u praksi, ali potpuno irelevantnih za nauku pa time i suštinski ograničene naučne vrednosti. U naučna istraživanja spadaju fundamentalna istraživanja, dok u stručna istraživanja spadaju primenjena i razvojna istraživanja. U praksi se često metodologija stručnog istraživanja poistovećuje sa metodologijom naučnog istraživanja. Međutim, razlika između ove dve metodologije je u tome što su u stručnom istraživanju niži kvalitet i pojednostavljenije procedure nego u naučnom istraživanju. Da bi istraživači mogli da kreiraju svoja naučna, naučno-stručna i stručna pisana dela, oni moraju imati znanja: o metodologiji naučnog istraživanja, tj. o naučnim metodama koje se mogu primenjivati u naučnim istraživanjima i o tehnologiji naučnog istraživanja, tj. o metodološkim postupcima transformacije ideja u pisana dela Faze istraživačkog rada Faze istraživačkog rada su: 1. izbor teme istraživanja, 2. proučavanje problematike, 3. definisanje problema i postavljanje hipoteza, 4. planiranje i modelovanje eksperimenta, 5. primena mera sigurnosti, 6. organizacija rezultata i analiza podataka i 7. prikazivanje rezultata Izbor teme Prvi korak u započinjanju istraživanja je izbor teme istraživanja. On je vrlo važan korak u naučnom radu, a istovremeno je i najkreativniji deo istraživanja. Pri izboru teme za istraživanje obično se daje odgovor na sledeća pitanja: 1. Šta se želi istraživati? 2. Da li ima smisla to istraživati? 3. Da li je to važno? 4. Da li je to naučno zanimljivo i intrigantno? Tema za istraživački rad se može pronaći sagledavanjem šta je aktuelni problem, šta je trend i šta je važno u odabranoj naučno oblasti. 4
6 Prilikom izbora teme istraživanja razmatra se: 1. Relevantnost planiranog istraživačkog rada, kojom treba da se odredi relacija očekivanih rezultata istraživanja sa naučnim saznanjima naučne grane i polja. 2. Naučni doprinos, koji daje odgovor na naučnost predloženog istraživanja. Ako očekivani rezultati istraživanja ne znače nove metode i postupke, nove činjenice kojima se potvrđuje ili opovrgava neka naučna hipoteza niti otvara novo područje istraživanja, ukratko, ako nije moguće u jednoj rečenici odgovoriti čime novim istraživanje doprinosi ljudskom znanju, onda se ne radi o naučno-istraživačkom radu nego o stručno-istraživačkom radu. 3. Procena štetnosti (za ljude, životinje, životnu sredinu) planiranog istraživanja, koja se odnosi na moguću štetnost postupaka istraživanja u toku istraživanja i 4. Procena etičnosti planiranog naučno-istraživačkog rada, danas je sve važnija posebno sa stanovišta povećane mogućnosti nauke da ostvare rezultati koji se mogu zloupotrebiti protiv čoveka i životne sredine Proučavanje problematike Kvalitetnom istraživanju prethodi proučavanje problematike kojom se istraživač namerava baviti. Nakon izvršenog prikupljanja literature ili paralelno s njim, prikupljene radove - reference treba pročitati, proučiti i obraditi. Time se istraživač upoznaje sa stanjem nauke i naučnim dostignućima, naučnim " backgroundom". Pri tome, najpre treba pročitati uopštene radove (pregledne radove) koji daju uvid u širu problematiku u području teme. Potom se može nastaviti s čitanjem radova koji tretiraju užu problematiku. Brojni su izvori naučnih i stručnih informacija, ali u naučnom radu najvažniji je izvor informacija literatura. Primarni izvori podataka su originalni naučni radovi i izveštaji o izvršenim originalnim naučnim istraživanjima. Sekundarni izvori podataka su izvori koji se zasnivaju na primarnim izvorima (enciklopedije, udžbenici, monografije, pregledni radovi) Definisanje problema i postavljanje hipoteze Uspešno sprovođenje naučnog istraživanja zahteva jasno definisanje njegove svrhe i ciljeva, koje se zasniva na poznavanju problema, jer u suprotnom će se sakupiti velika količina informacija, a neće biti ideje šta s njima. Zato treba definisati kako se planirana istraživanja uklapaju u širu problematiku nauke, odrediti ključne parametre istraživanja, tako da se mogu planirati metode za obradu uzoraka i analizu podataka. Ako se radi o planiranju eksperimentalnih istraživanja, potrebno je odlučiti koje će se varijable držati konstantnim ili kontrolisanim, a koje će biti promenljive. Ako naučno istraživanje uključuje statističku obradu suštinsko je da se uzorkovanje izvrši slučajnim izborom koristeći tabelu slučajnih brojeva. Za određivanje načina za postizanje cilja potrebno je postavljati pitanja i time definisati problem. Pitanja se definišu na osnovu saznanja istraživača o stanju nauke i naučnim rezultatima te refleksije cilja istraživanja na naučna saznanja. Postupak postavljanja pitanja predstavlja jedan oblik metode idealnih tipova, tj. zapravo je naučni oblik priželjkivanog mišljenja, i znači pretpostavku posmatranja za postizanje željenog, očekivanog ili planiranog cilja. Svako od ovih posmatranja, definisanih kao pitanje predstavlja privremena predhipotezu, pripremu hipoteze. Postavljanjem potrebnog i dovoljnog broja pitanja, kojima su dobijeni odgovori na sva stanovišta problema, definisan je dovoljan broj predhipoteza čijom sintezom se definiše jedna ili više hipoteza. 5
7 Planiranje i modelovanje eksperimenta Naučno istraživanje, nakon definisanja jedne ili više hipoteza, ulazi u fazu potvrđivanja (verifikacije) ili opovrgavanja hipoteze (falsifikacije). U ovoj fazi sprovodi se, saglasno usvojenoj hipotezi, postupak provere prognoze (predviđanja) rezultata budućeg opažanja, eksperimenta ili simulacije, što znači predviđanje budućeg prirodnog događaja, budućeg eksperimentalnog događaja ili rezultata simulacije. Ako potvrđivanje hipoteze zahteva proveru prognoze eksperimentom, prvi korak u planiranju eksperimenta je određivanje broja i vrste podataka kojima se proverava hipoteza potvrdom ili opovrgavanjem prognoze. Ispravno modelovan eksperiment daje relevantne podatke potrebne za potvrdu hipoteze i sastoji se samo od onih eksperimentalnih aktivnosti potrebnih za dobijanje planiranog broja i planirane vrste podataka. Podaci, koji nisu u funkciji potvrde prognoze, bez obzira na njihovu moguću korisnost, suštinski su rezultat nepreciznog modelovanja eksperimenta ili nekorektnog planiranja. Zato u planiranje, modelovanje i sprovođenje eksperimenta treba uključiti: 1. Izbor samo onih podataka vezanih za prognozu (podaci koji potvrđuju ili opovrgavaju prognozu). 2. Modelovanje eksperimenta na osnovu traženih podataka. 3. Definiciju kontrolnog događaja. 4. Izbor metoda merenja, opažanja i beleženja onoga što se događa u svakoj fazi eksperimenta. 5. Planiranje vremenskih rokova za svaku fazu eksperimenta. 6. Realizaciju eksperimenta. i 7. Analizu svih dobijenih rezultata (ne treba odbacivati negativne rezultate jer nema negativnih rezultata eksperimenta već samo postoje rezultati koji u kontekstu eksperimenta nisu ispravno interpretirani) Mere sigurnosti prilikom izvođenja eksperimenta U praksi naučnih istraživanja pojavljuju se i eksperimenti, koji zahtevaju i upotrebu opasnih organizama, hemikalija ili opreme, pa u rukovanju s njima treba preduzeti sve propisane mere bezbednosti i zdravlja na radu, kao i zaštite životne sredine. Pri planiranju eksperimenata takvih naučnih istraživanja sve aktivnosti i procedure treba kontrolisati, uvažavajući moguće opasnosti i štetnosti, koje mogu nastati zbog neprimenjivanja zaštitnih sredstava i opreme pri ispravnom radu eksperimentalne opreme ili zbog kvara ili neispravnog rada opreme. Potencijalne opasnosti tokom izvođenja različitih eksperimenata mogu biti: 1. Biološke kulture (bakterije, virusi, gljivice itd.). 2. Hemijske materije (toksične, agresivne). 3. Električni i mehanički aparati (struja, visoki napon, opasnost od mehaničkih povreda). 4. Opasnost od požara. 5. Izloženost radijaciji. 6. Izloženost od izlaganja laserskim zracima. 7. Izloženost UV svetlu. 8. Izloženost X-zračenju. 6
8 9. Izloženost mikrotalasnim zračenjima. 10. Izloženost poljima radiotalasa visokog intenziteta. 11. Izloženost radioaktivnom zračenju (β, γ) Organizacija rezultata i analiza podataka Tokom istraživanja vrlo je važno pažljivo beležiti dobijene rezultate u unapred definisanu tabelu. Dobijene rezultate treba analizirati i ako je to potrebno i statistički obraditi. Na primer, ako se dve ili više aritmetičkih sredina značajno statistički razlikuju primenom analize Studentovim t-testom (u slučaju dve aritmetičke sredine) ili primenom analize varijansi (za poređenje više od dve aritmetičke sredine), to je dokaz da polazna hipoteza nije dobro postavljena. Najvažnija prepostavka za većinu osnovnih statističkih testova (parametarski testovi) je normalna raspodela podataka (to znači da će vrednosti podataka nacrtane u odnosu na njihovu frekvenciju dati karakterističnu krivu normalne raspodele). Ako podaci nisu normalno raspodeljeni tada treba izbegavati parametarske testove i primeniti neparametarske testove. Kod primene statističke obrade posebno je važno kontrolisati značajnost, statističkom obradom, dobijenih rezultata. Osnovni statistički postupci s kojima se istraživači, u pretežnom broju istraživanja, redovno susreću su: aritmetička sredina, raspon, standardna devijacija, varijansa, standardna greška aritmetičke sredine, granice pouzdanosti Prikazivanje rezultata Za prikazivanje rezultata u istraživačkoj praksi najčešće se koriste: tabele i dijagrami. Ako je informacije moguće izraziti tekstualno tada nema potrebe koristiti tabelu ili dijagram Metode istraživanja Razvijene su brojne metode koje nauka koristi u naučnim istraživanjima, da bi se istražio naučni problem i da bi se došlo do naučnih saznanja. Prema nivou opštosti, naučne metode (metode istraživanja) se dele na: posebne naučne metode, opšte naučne metode i tehničke metode. 1. Posebne naučne metode 7
9 Neke posebne naučne metode se primenjuju u svim naučnim područjima a neke se primenjuju samo u nekim naučnim područjima. Posebne naučne metode: metoda analize i sinteze, metoda apstrakcije i konkretizacije, metoda generalizacije i specijalizacije, metoda klasifikacije, metoda indukcije i dedukcije, metoda dokazivanja i opovrgavanja aksiomatska metoda, istorijska metoda, metoda deskripcije, metoda kompilacije, dijalektička metoda, genetička metoda, metoda merenja, metoda mozaika itd. 2. Opšte naučne metode Opšte (osnovne) naučne metode se primenjuju bez obzira na naučno područje, naučno polje, naučnu granu, naučnu disciplinu ili interdisciplinarno naučno područje. Opšte naučne metode su: empirijska metoda, metoda modelovanja, statistička metoda, metoda crne kutije, matematička metoda, komparativna metoda, kibernetička metoda, metoda teorije sistema, analitičko-deduktivna metoda itd. 3. Tehničke metode Tehničke metode, su: metoda posmatranja (opažanja), eksperimentalna metoda, metoda naučnog ispitivanja: o metoda intervjuisanja, 8
10 o metoda anketiranja, o metoda brojanja, informatička metoda, metoda studije slučaja itd Empirijska metoda Empirijska metoda se zasniva na iskustvu, radi objašnjavanja nekih pojava, sudova i zaključaka. Ona omogućava pristup istraživanjima i izvođenje eksperimenta bez postavljanja hipoteze ili nastojanja da se ona dokaže. Kao nepotpuna eksperimentalna metoda, često se u literaturi pominje empirijska metoda, u kojoj pristupamo istraživanju bez postavljanja naučne hipoteze. Istraživanja koja se sprovode ovom metodom smatraju se prethodnim eksperimentima, na osnovu kojih se mogu postavljati radne hipoteze i preduzimati nova naučna istraživanja kako bi se te hipoteze verifikovale. Može se recimo, koristiti u poljoprivredi, ako se, na primer, želi da ispita prinos novih vrsta biljaka, ili u farmaceutskoj industriji prilikom testiranja novih lekova itd. Rezultati do kojih se dolazi ovom metodom su vrlo važni, pre svega za praktičnu primenu, ali i za nauku, jer oni najčešće predstavljaju fazu prikupljanja naučnih činjenica na osnovu kojih se utvrđuju zakonitosti Metoda posmatranja Metoda posmatranja je organizovano posmatranje u cilju otkrivanja novih činjenica ili proveravanja naučnih hipoteza. Naučno posmatranje kao metoda može da prethodi svakoj drugoj metodi, a pre svih eksperimentalnoj metodi. Pažljivo posmatranje je neizbežno kao samostalan čin u prirodnim uslovima, zatim prilikom eksperimentisanja, kao i u uslovima koje stvara praktičan život. Može se primeniti u svim naučnim područjima i naučnim disciplinama u kombinaciji s drugim naučnim metodama. Da bi posmatranje bilo naučno-saznajno vredno, mora biti: što objektivnije, što svestranije i što potpunije, što preciznije i što strože, što sistematičnije. Naučno posmatranja može biti: neposredno (direktno) posmatranje indirektno posmatranje, sveobuhvatno posmatranje (predmet posmatranja je neka složena i dugotrajna pojava), masovno posmatranje (predmet posmatranja je neka masovna pojava), pojedinačno posmatranje (predmet posmatranja je neka pojedinačna pojava redak i jedinstven fenomen), sistemsko posmatranje. 9
11 2. EKSPERIMENTALNA ISTRAŽIVANJA Eksperiment je latinska reč (experimentium) što u prevodu znači ogled (opit, pokus ili proba). Eksperimnet je jedna od najvažnijih, najobjektivnijih i najegzaktnijih naučnih metoda, tako da saznanja zasnovana na njemu imaju visok naučni značaj. Eksperiment je metod naučnog istraživanja u kojem se namerno i sistematski menja neka pojava, da bi se izazivala, a onda posmatrala i merila neka druga pojava, dok se ostali relevantni uslovi (promenjive) kontrolišu ili pak izoluju. Eksperimentalna metoda je postupak organizovanog posmatranja, kojim se predmet istraživanja izlaže više puta različitim uslovima u pogledu temperature, pritisaka i drugih fizičkih, hemijskih i ostalih uticaja, uz pomno beleženje promena koje se pri tome dešavaju. Faktori koji utiču na eksperiment, a ne uzimaju se u obzir nazivaju se spoljni faktori (eliminišu se ili drže konstantnim). Spoljni faktori remete uticaj osnovnih faktora smanjujući tačnost rezultata. Eksperimentalna metoda se često koristiti sa drugim naučnim metodama, naročito sa metodom posmatranja. Eksperiment je analitički postupak za proučavanje uzročno-posledičnih veza. Eksperiment u osnovi predstavlja pokušaj i posmatranje. Postoji više vrsta eksperimenata, a najpoznatiji su: eksperimenti u laboratorijskim uslovima, eksperimenti u prirodnim uslovima, veštački (ispitivanje inteligencije ljudi pomoću testova), eksperimenti (simulacije) na računaru itd. Bitna saznajna uloga eksperimenta je u: proveravanju činjenica koje su ranije utvrđene, ali koje nisu potpuno pouzdane (proveravanju hipoteza, naučnih zakona, stavova i teorija), otkrivanju novih naučnih činjenica o pojavama koje se istražuju (postavljanju novih, konkretnijih, adekvatnijih i specijalnijih hipoteza). U svim slučajevima eksperiment je tako organizovan postupak stručnog i/ili naučnog istraživanja, da dobijeni rezultat nesumljivo i nedvosmisleno potvrđuje ili odbacuje postavljenu hipotezu. Eksperiment kojim se razrešava protivrečnost između dve različite hipoteze naziva se krucijalni (putokazni) eksperiment. Hipoteza je razumna pretpostavka zasnovana na prethodnim opažanjima i stečenim znanjima, koju treba dokazati. Cilj eksperimenta je da pruži odgovor na ne istraženo pitanje. Naučni eksperiment je metoda praktično-teorijskog saznanja, čiju strukturu čine: eksperimentator (pojedinac ili grupa istraživača koji vrše eksperiment), predmet eksperimenta (realni sistemi, pojave i procesi, njihovi kvaliteti, kvantiteti, mere, načini nastanka, promene itd.), sredstva eksperimenta (materijali eksperimenta, instrumenti, uređaji, mašine, postrojenja itd.), 10
12 postupci eksperimenta (odabiranje vrste ogleda, izdvajanje ogledne grupe, teorijskopraktične operacije, postavljanje hipoteza i njihova provera), eksperimentalni proces (uslovi eksperimentalne situacije, fizički i hemijski procesi i drugo), rezultati eksperimenta, i interpretacija rezultata eksperimenta i izvođenje naučnih pretpostavki i zakona. Obrada rezultata eksperimenta je završni deo rada eksperimentalnog istraživanja i sastoji se iz: provere podataka, određivanje greške eksperimenta ili njenog merila, provere hipoteze, sređivanje rezultata u obliku prikazivanja. Rezultati eksperimenta moraju dati što više verodostojnih informacija. U inženjerskim eksperimentima najčešće se zahteva kvantitativno prikazivanje rezultata u obliku funkcija ili grafikona. Planiranje naučnog eksperimenta je podešavanje pojava tako da eksperimentalni proces odgovori na postavljeno pitanje i da se izvrši organizovanje ogleda. Prvi korak u eksperimentalnom istraživanju može da bude uspešno mehaničko shvatanje po kome jedan uzrok ima jednu posledicu. U najvećem broju slučajeva i u različitim oblastima istraživanja koriste se tzv. test funkcije na ulazu u sistem. Sledeći koraci u istraživanju mogu da budu usmereni na upoznavanje funkcionisanja sistema. Zadatak različitih, više ili manje razrađenih i primenljivih metoda eksperimentalnog istraživanja jeste upućivanje istraživača na moguće postupke eliminacije. Eksperimentalna metoda se primenjuje široko u gotovo svim oblastima nauke. Danas je u primeni veliki broj eksperimentalnih metoda u tehničkoj dijagnostici za procenu stanja tehničkih sistema. Ovde treba reći da se kao deo svakog eksperimenta mora tretirati postupak merenja. Obično struktura postupaka merenja sadrži: merni objekat - nosilac merne veličine, merni signal primarni signal, prijemnik signala, merni signal (preslikani signal), korekturni član računski element, korigovani preslikani signal, optički instrument pokazivač, merna vrednost, registrovanje, memorisanje, obrada podataka (računar), i očitavanje i dr. 11
13 3. ISTRAŽIVANJA METODOM MODELOVANJA 3.1. Pojam modelovanje Direktna istraživanja na velikim i složenim sistemima (kao što su: tehnički, poslovni, ekonomski, vojni itd.) po pravilu su vrlo skupa (zahtevaju puno resursa i vremena), teško, a ponekad i nemoguće izvodljiva, naročito u fazi njihovog planiranja, projektovanja i uvođenja u rad. Da bi se olakšala istraživanja (proučavanja) ovakvih sistema često se ona vrše metodom modelovanja. Istraživanje realnog sistema metodom modelovanja podrzumeva da se realni sistem predstavi (zameni) modelom, tako da se umesto na realnom sistemu istraživanja vrše na njegovom modelu, a zatim se dobijeni rezultati sa modela prenose na realni sistem (pojavu), pri tome se istraživanja na modelu mogu vršiti eksperimentalno ili simulacijom na računaru. Model je na pojednostavljen (uprošćen) način predstavljen (prikazan) neki realni sistem (fenomen ili proces). Model nikada potpuno verno ne predstavlja realni (stvarni) sistem, već je uvek u nekoj meri pojednostavljen. Koliko će model biti pojednostavljen (odnosno složen) zavisi od njegove namene. Nalaženje prave mere pojednostavljenja (apstrakcije) realnog sistema često nije jednostavno, i tu u punoj meri do izražaja dolazi inženjerska veština i intuicija (znanje stečeno iskustvom). Nivo pojednostavljenja (apstrakcije) realnog sistema utiče na validnost modela. Validnost modela pokazuje koliko je verno (uspešno) realni sistem predstavljen preko modela. S jedne strane model treba da bude složen kako bi dovoljno verno predstavljao (opisivao) realni sistem, dok sa druge strane model treba da bude što jednostavniji kako bi se sastojao od jednostavnijih algoritama, a time bio jeftiniji i lakši za istraživanja, a simulacije se brže izvodile na računaru. Prilikom izrade modela realnog sistema nikada se u model ne ugrađuju sve karakteristike realnog sistema, nego samo one koje su bitne za njegovo proučavanje (nebitne karakteristike se zanemaruju). Tako da je model u bitnim karakteristikama analogan sa realnim sistemom (predmetom modelovanja), što omogućava da se do određenih saznanja o realnom sistemu (o ponašanju, efikasnosti i drugim bitnim karakteristikama) dođe preko modela, tj. na osnovu rezultata istraživanja na modelu. Prilikom prenosa dobijenih rezultata istraživanja sa modela na realni sistem treba voditi računa o pretpostavkama i zanemarenjima, uz koje je formiran model realnog sistema, jer samo uz te pretpostavke i zanemarenja vrede dobijeni rezultati istraživanja. Model treba da se pod istim pretpostavkama ponaša kao realni sistem. Strukturu modelovanja čine: predmet modelovanja, je realni sistem koji se istražuje (proučava), 12
14 model, je predmet koji zamenjuje realni sistema sa kojim je analogan u bitnim karakteristikama i čovek (prisutna svest). Prilikom istraživanja realnog sistema metodom modelovanja mogu nastati dve teškoće: da li je model validna predstava realnog sistema (pojave) i ispravnost prenošenja dobijenih rezultata sa modela na realni sistem (pojavu). Modeli mogu biti: jednostavni (fizički model aviona u aerodinamičkom tunelu) i veoma složeni matematički modeli (optimizacioni i simulacioni modeli strateškog sistema odbrane, planiranja realizacije složenih objekata, sistema i procesa) Ciljevi modelovanja Istraživanje realnih sistema metodom modelovanja omogućava da se: bolje razumeju realni sistemi (fizički, biološki i društveni itd.) sa kojima je model u bitnim karakteristikama analogan; bolje razumeju i planiraju eksperimenti; steknu nova saznanja o realnim sistemima preko njihovih modela, čime se smanjuju nesigurnosti vezane za realne sisteme (fenomene ili procese) koje se model predstavlja; predvidi ponašanje realnih sistema (fenomena ili procesa) u budućnosti; obave različite simulacije, koje mogu od biti velike pomoći prilikom donošenja određenih odluka. Modeli omogućavaju da se postavljaju pitanja šta ako, koja su vezana za moguće promene u stanju ili funkcionisanju sistema (fenomena ili procesa) u određenim uslovima; projektuju uređaji i postrojenja; ispitaju postojeći uređaji; izvrši optimizacija i efikasnije upravljanje realnim sistemima; kontrolišu neželjeni događaji; izbegnu opasnosti koje mogu uzrokovati eksperimenti nad realnim sistemima; reše različiti problemi u tekućoj proizvodnji; osvoje nove tehnologije ili proizvodi; kreiraju novi (originalni) tehnološki postupci, tehnološki sistemi, oprema, uređaji, inovacije itd Primeri upotrebe modelovanja Istraživanja realnih sistema metodom modelovanja se koriste u različitim oblastima, kao što su: Marketing: Ako je cena proizvoda porasla, koliko će potražnja opasti? 13
15 Nabavka: Ako postoji više izvora sirovina i više postrojenja, kako rasporediti sirovine po postrojenjima? Sinteza: Кoji procesi su neophodni za proizvodnju željenog proizvoda? Projektovanje: Кoji tipovi uređaja i kojih dimenzija su neophodni za produkciju proizvoda? Proizvodnja: Кoji operativni uslovi će dati maksimalni prinos proizvoda? Upravljanje: Кako se izlazna veličina može održavati na željenoj vrednosti pomoću manipulativne promenjive? Bezbednost: Ako se dogodi otkaz uređaja kako će to uticati na operatera i ostalu opremu? Životna sredina: Кoliko će trajati razgradnja opasnog otpada u zagađenom zemljištu? 3.4. Podele modela Prema ulozi čoveka u nastanku predmeta modelovanja, modeli se dele na: modele prirodnih sistema (mikrofizičke, makrofizičke), i modele veštačkih sistema, koji se dele na: o modele tehničkih sistema i o modele društvenih sistema. Prema obliku postojanja, modeli se dele na: materijalne (realne, fizičke) modele (hemijska struktura molekula, model aviona), i apstraktne (idealne, misaone) modele, koji se dele na: o govorne (verbalne) modele, o opisne modele, o grafičke modele (geometrijske, simboličke (konceptualne, matematičke, računarske)), i o formalne modele (matematičke, logičke). Prema nameni modeli se dele na: saznajne modele, demonstracione modele, konstrukcione modele i modele optimizacije i upravljanja. Prema svojstvu predmeta modelovanja modeli se dele na: modele funkcije, modele ponašanja i modele građe. Prema nameni, modeli se dele na: deskriptivne, 14
16 prediktivne ili normativne. Deskriptivni modeli uglavnom opisuju postojeće ili prošlo stanje sistema. Na taj način oni omogućavaju predstavljanje sistema bez mogućnosti prognoziranja budućih stanja, odnosno pružanja eksplicitnih informacija o normativnom upravljanju sistemom. Tipični predstavnici deskriptivnih modela su: geografske mape, organizacione šeme, završni račun preduzeća i slično. Кao što se može zaključiti, ova vrsta modela ne pruža ništa više od opisa postojećeg stanja sistema, ali omogućava bolje sagledavanje interakcija objekata u sistemu. Prediktivni modeli služe za analizu posledica različitih strategija upravljanja sistemom. Pomoću njih se može predvideti rezultat donesenih odluka. Tipično, ova vrsta modela povezuje zavisne i nezavisne promenljive vrednosti koje opisuju stanja sistema na taj način da se mogu dobiti prognozirane vrednosti zavisnih promenljivih na osnovu pretpostavljenih vrednosti nezavisno promenljivih. Sa ovom vrstom modela se može dobiti odgovor na pitanje šta ako, tj. šta će se desiti sa vrednostima zavisnih promenljivih, ako nezavisno promenljive uzmu zadate vrednosti. U ovu vrstu modela spada većina simulacionih modela kao regresivni modeli, modeli simultanih jednačina, PERT modeli, modeli redova čekanja i slično. Normativni modeli služe da pruže informacije kako treba upravljati sistemom da se postigli željeni ciljevi. Ovi modeli omogućavaju da se izabere optimalno rešenje iz skupa mogućih rešenja. Osnovni problem kod ovih modela je izbor jedne ili više funkcija cilja koje treba optimizirati. Tipični normativni modeli su: modeli linearnog programiranja i uopšte modeli matematičkog programiranja, modeli upravljanja zalihama i slično. Prema tome da li se promenljive menjaju tokom vremena, modeli se dele na: statičke i dinamičke. Кod statičkih modela relacije među objektima se ne menjaju sa vremenom, dok kod dinamičkih modela zavisnost od vremena postoji. Može se zaključiti da su u opštem slučaju, dinamički modeli složeniji od statičkih, ali i da su u većini slučajeva bliži realnom sistemu. Prema tome da li postoji faktor slučajnosti, modeli se dele na: determinističke modele, modele rizika, modele neizvesnosti i konfliktne modele. Deterministički modeli se karakterišu odsustvom slučajnog faktora. Drugim rečima, verovatnoća realizacije bilo kog stanja okoline (a samim tim i sistema) kod ovih modela je jednaka jedinici. Кod modela rizika poznata su stanja okoline i mogu se opisati odgovarajućim verovatnoćama. Prema tome, promenljive modela su slučajne promenljive čije su raspodele verovatnoća poznate. Modeli neizvesnosti se karakterišu nepoznavanjem budućih stanja okoline i odgovarajućih raspodela verovatnoća i najbliži su većini realnih situacija. Međutim, njihova snaga je relativno ograničena s obzirom da su u opštem slučaju nerešivi. Uvođenjem koncepta subjektivnih verovatnoća ovi modeli se prevode u modele rizika sa poznatom procedurom rešavanja. 15
17 Кod konfliktnih modela koji čine osnovu teorije igara, stanja okoline su pod kontrolom drugog igrača (ili više ostalih igrača) koji čine oponenciju ili konkurenciju prvom igraču (donosiocu odluka). Sve igre uključujući i ratne, mehanizam konkurencije na tržištu i slično se mogu opisivati ovom vrstom modela, kao što je slučaj sa svim modelima planiranja i predviđanja. Prema stepenu opštosti, modeli se dele na: specijalizovane i opšte. Opštost se odnosi na mogućnost primene modela na različite situacije. Opšti modeli se mogu koristiti za rešavanje različitih tipova problema. Primeri opštih modela su: linearno programiranje, modeli redova čekanja i slično. Specijalizovani modeli se prave za rešavanje određenog pojedinačnog problema i ne mogu se prenositi na druge situacije. U dosta slučajeva opšti modeli ne obezbeđuju efikasno rešavanje postavljenog problema i tada se pribegava gradnji specijalizovanih modela koji su po pravilu ekonomičniji. Prema strukturi, modeli se dele na: ikoničke, analogne i simboličke. Ikonički modeli su slika u malom ili u velikom sistema koji predstavljaju i zadržavaju određene fizičke osobine sistema. Po svojoj suštini ova klasa modela je najjednostavnija za razumevanje i obezbeđuje stepen korisnosti koji nije prisutan kod ostalih vrsta modela. Oni vizuelno liče na realni sistem koji predstavljaju i veoma su ograničeni u mogućnosti istraživanja uzročno-posledičnih relacija u sistemu. Tipični ikonički modeli su: modeli aviona u vazdušnom tunelu, modeli hidrograđevinskih objekata (brane itd.), modeli atoma i slično. Analogni modeli koriste osobine jednog fizičkog sistema (modela) da bi se predstavile osobine drugog fizičkog sistema (realnog sistema). Na taj način se uspostavlja analogija između raznorodnih fizičkih veličina (npr. analogija tokova struja sa vodenim tokovima). Elementi i relacije u realnom sistemu se zamenjuju elementima i relacijama u analognom modelu koga je jednostavnije analizirati nego realni sistem. U modelu postoji jaka korespondencija između njegovih elemenata i elemenata realnog sistema. Tipični analogni modeli su: graf sistema u kome se dužine koriste da predstave međusobne relacije elemenata, PERT mreže, modelovanje na analognom računaru i slično, vezano za proces planiranja i predviđanja. Simbolički modeli - češće se nazivaju matematički modeli objekte i relacije realnog sistema zamenjuju odgovarajućim simbolima koji se vezuju za osobine objekata i koje nazivamo promenljivima, i simbolima koji predstavljaju relacije među promenljivima i koje nazivamo operatorima. Ova vrsta modela je visokog stepena opštosti i apstrakcije i njima se uvodi matematički način rezonovanja u analizi sistema. Prema sličnosti i analogiji modela s predmetom modelovanja modeli se dele na: slične modele i analogni modele 16
18 Pri ovome treba napomenuti da su sve pojave (ili svi predmeti) slične ako su iste prirode (dve pumpe za vodu), a analogne, ukoliko su različite prirode (prelaz toplote diferencijalna jednačina). Fizička sličnost modela i predmeta modelovanja obuhvata: geometrijsku sličnost (geometrijska sličnost granica i sličnost položaja), kinematičku sličnost (odnos vektora brzina i ubrzanja) i dinamičku sličnost (odnosi vektora sila i tenzora napona u prostorno-vremenskim tačkama za celo područje moraju biti konstantni). Potpunu fizičku sličnost je teško postići, jer koeficijenti sličnosti pojedinih fizičkih veličina nisu međusobno nezavisni, uslovljeni su fizičkim zakonima. Fizička analogija. - U slučaju da se žele rezultati ispitivanja fizičkih pojava, s jednog područja fizike, preslikati na pojave drugačije prirode, to nije moguće učiniti na osnovu fizičke sličnosti. U tom slučaju se radi o traženju analogija između posmatranih pojava. U fizici se koristi fizička analogija. U oblasti tehničkih sistema značajna je matematička analogija. Različite dimenzije pojava obuhvaćene matematičkom analogijom obrazuju matematičku analošku grupu. Prema stepenu kvantifikacije modeli se dele na: kvalitativne i kvantitativne. Кvalitativni modeli se odnose na sisteme kod kojih nije moguće uvesti merenje karakterističnih veličina ili nije moguće uraditi matematički model. Кao takvi, kvalitativni modeli su manje precizni, manje racionalni i manje konzistentni od kvantitativnih modela. Međutim, veoma često oni su jedini mogući način opisa realnosti. Dok kvantitativni modeli koriste matematičke relacije i rezultate iskazuju numerički, kvalitativni modeli ne izražavaju se formalnim jezicima i rezultati nisu numerički. Кvalitativni modeli uzimaju u obzir i prisustvo ljudskog faktora u sistemima koji se po pravilu zanemaruju kod kvantitativnih modela. Кvalitativni modeli se mogu podeliti na: mentalne i verbalne. Кvantitativni modeli se iskazuju formalnim matematičkim jezikom uz pretpostavku da se svi atributi objekta sistema koji se modeluje mogu meriti. Кvantitativni modeli su tipični za prirodne i tehničke nauke, ali je sve veća njihova upotreba u društvenim naukama, naročito u ekonomiji, planiranju i vojnim naukama. Osnovni nedostatak kvantitativnih modela leži u činjenici da veći broj promenljivih, karakteristični za dati problem ne podleže merenju, kao i da složenost relacija realnog sistema često nije moguće iskazati odgovarajućim matematičkim relacijama modela. Postoji: neformalni opis modela i formalni opis modela. Neformalni opis modela, daje osnovne pojmove o modelu i najčešće nije potpun i precizan. Neformalni opis je dosta brz i lak te zbog toga može biti nekompletan (ne sadrži sve situacije koje mogu da nastupe), nekonzistentan (predviđanje dva ili više pravila za istu 17
19 situaciju kontradiktorne akcije), nejasan (ako nije definisan redosled akcija). Ovakve situacije se prevazilaze pravilima i konvencijama u komuniciranju zvanim formalizmi. Formalni opis modela, treba da obezbedi veću preciznost, potpunost u opisivanju modela. Omogućava i formalizovanje nekompletnosti, nekonzistentnosti i nejasnosti kao i usmeravanje pažnje na karakteristike objekata koje su od najvećeg značaja za istraživanje (apstrakcija). Osnovne vrste modela su: mentalni (misaoni) modeli, verbalni (govorni) modeli, fizički modeli, konceptualni modeli, matematički modeli i računarski modeli. Mentalne (misaone) modele konstruiše ljudski um i na osnovu toga deluje. Omogućavaju komunikaciju među ljudima, planiranje aktivnosti itd. Mentalni modeli su prvi nivo apstrakcije nekog problema ili situacije. Кad god neko nešto misli o nečemu to je mentalni model. Prema tome, po definiciji različiti ljudi poseduju različite mentalne modele o istoj pojavi. Verbalni (govorni) modeli su direktna posledica mentalnih modela i predstavljaju njihov izraz u govornom jeziku. Obično se predstavljaju u govornom obliku i spadaju u klasu neformalnih modela. Na taj način se prevazilazi inherentna nekomunikativnost mentalnih modela koji su svojina isključivo jednog čoveka. Konceptualni modeli se formiraju na osnovu strukture i logike rada sistema. Zovu se još i strukturni modeli pošto u grafičkom obliku ukazuju na strukturu sistema te su pogodno sredstvo za komunikaciju. Predstavljaju osnovu za izradu matematičkih modela. Sastoje se od blok dijagrama ili dijagrama tokova (predstavljaju grafički prikaz povezanosti elemenata sistema na način kako se formiraju kola povratnog dejstva i onako kako se kola sprežu stvarajući sistem). Fizički modeli predstavljaju umanjene ili uvećane predstave realnih sistema. Ponašaju se kao njihovi originali a prave se na osnovu sličnosti sa realnim sistemom ili fizičkih zakona. Analiza fizičkih svojstava na manjem modelu i relacije sa većim objektom analiza sličnosti. Matematički modeli predstavljaju skup matematičkih (analitičkih) jednačina (izraza, relacija) koje opisuju ponašanje realnog sistema. Matematički modeli imaju veću preciznost od verbalnih modela. Računarski predstavljaju prikaz matematičkih modela u obliku računarskih programa korišćenjem programskih jezika i usko su vezani za razvoj računarske nauke. Postupak izrade modela nekog realnog sistema se sastoji u izradi mentalnog modela i njegovoj transformaciji u konceptualni, zatim u transformaciji konceptualnog u matematički, a potom matematičkog u računarski model, sve dok se ne izradi željeni model. 18
20 4. MATEMATIČKO MODELOVANJE Matematički modeli predstavljaju skup matematičkih (analitičkih) jednačina (izraza, relacija) koje opisuju ponašanje realnog sistema. Matematički modeli se formiraju postavljanjem odgovarajućih matematičkih jednačina (diferencijalnih, algebarskih ili logičkih) koje opisuju ponašanje realnog sistema u stacionarnom (ustaljenom) ili u dinamičkom (prelaznom) stanju. Matematčke (analitičke) jednačine koje opisuju ponašanje realnog sistema mogu biti: Linearne jednačine: Nelinearne jednačine: Algebarske jednačine: Diferencijalne jednačine: Integralne jednačine: Prilikom postavljanja matematičkih jednačina koriste se zakoni fizike (kao što su: zakon o održanju mase i energije, impulsu kretanja, Bernulijeva jednačina, itd.). Za električne sisteme od posebnog značaja su: Kirhofovi zakoni, Omov zakon, zakon elektromagnetne indukcije, Maksvelove jednačine itd. Matematički modeli se koriste još od vremena kada su razvijene diferencijalne jednačine. Međutim, njihov značaj dolazi do punog izražaja tek sa razvojem računara na kojima se mogu vršiti simulacije ponašanja realnih sistema. Svaki matematički model je zasnovan na određenim pretpostavkama koje pojednostavljuju matematički model. Pretpostavke zavise od ciljeva istraživanja realnog sistema i treba da budu realne (zasnovane na teorijskim osnovama, eksperimentalnim saznanjima, iskustvu i osećaju inženjera) i da ne unose dodatne greške u model. Matematički modeli se mogu rešavati: analitički i numerički. Rešavanje matematičkih modela analitički se vrši primenom matematičke teorije, teorema, zakona i sl. Koristi se kada su u pitanju jednostavniji problemi, kao što su: algebarske i jednostavnije diferencijalne jednačine. Rešavanjem matematičkih modela analitički dobija se tačniji rezultat. 19
21 Rešavanje matematičkih modela numerički se vrši primenom numeričkih metoda i upotrebom programskih jezika (često upotrebom gotovih programskih paketa) i digitalnih računara. Koristi se za rešavanje složenijih jednačina. Tačnost rešavanja matematičkih modela numerički zavisi od preciznosti upotrebljene numeričke metode. Tačnost matematičkih modela se najadekvatnije proverava poređenjem rezultata istraživanja dobijenih na modelu sa rezultatima dobijenim odgovarajućim eksperimentima. Tačnost modela se najčešće kvantifikuje pomoću srednje greške (apsolutne, relativne, razlike kvadrata, standardne devijacije itd.). Model se može verifikovati i na osnovu fizičke konzistentnosti (proverom zakona o održanju mase i energije, eliminacijom zbog fizičkih nemogućih rezultata, npr. negativna temperatura, zapremina i dr.). Način validacije modela i interpretacije greške zavisi od ciljeva modela i načina rešavanja. Validnost modela zavisi i od utroška računarskog vremena i resursa. Uzroci grešaka matematičkih modela su: Pogrešne (nerealne) pretpostavke. Preveliko pojednostavljenje problema. Pogrešna matematička formulacija problema. Pogrešne vrednosti konstanti (ulaznih) podataka. Izbor neadekvatne numeričke metode. Pogrešan redosled postupaka u algoritmu. Velika tolerancija u numeričkoj metodi. Prema tome na koji način se promenljive modela menjaju tokom vremena, modeli se dele na: Diskretne modele, u njima se promenljive menjaju samo u pojedinim tačkama tokom vremena, nema kontinualne promene stanja. Te promene se nazivaju događaji. Kontinualne modele, u njima se promenljive menjaju kontinualno tokom vremenu. Na digitalnim računarima se ne mogu izvoditi kontinualne promene veličina već se moraju aproksimirati skupom diskretnih vrednosti. Kontinualno-diskretne modele, sadrže i kontinualne i diskretne promenljive. Postoji veliki broj matematičkih modela koji se mogu koristiti za proučavanje ekoloških sistema. Postoji više načina prema kojima se matematički modeli mogu podeliti, kao što su: U kojoj meri se modeli zasnivaju na teoriji ili observacijama teorijski nasuprot empirijskim modelima. U kojoj meri nasumični (slučajni) događaji i efekti imaju značajnu ulogu u proučavanom sistemu, a samim tim i u modelu deterministički nasuprot stohastičkim modelima. U kojoj meri se raspolaže znanjem o proučavanom sistemu koji model treba da predstavlja model crne kutije (Black box) nasuprot modelu bele kutije (White box). Da li se model bavi realnim procesima koji su statični ili dinamični u odnosu na prostor i vreme statički nasuprot dinamičkim modelima. Da li se model bavi realnim procesima za koje se uzima da funkcionišu na kontinualan ili diskretan način kontinualni nasuprot diskretnim modelima. 20
22 Kako su prostorno uređeni podaci modela modeli sa raspodeljenim parametrima nasuprot modelima sa grupisanim parametrima. 1. Model crne kutije (Black box) i model bele kutije (White Box) S obzirom na to koliko su poznati struktura, sastav i način funkcionisanja proučavanog realnog sistema, matematički modeli se dele na: modele crne kutije (Black box) (providni), modele bele kutije (White Box) (zatamnjeni) i modele sive kutije (Gray box) Pod modelom crne kutije podrazumeva se model realnog sistema (pojava) koji se istražuje i koji se posmatra kao zatvorena kutija čija se strukturna građa ne poznaje (slika 2.3.). Pojednostavljeno rečeno, bez otvaranja kutije, praćenjem šta se dešava na ulazu i izlazu, težimo da saznamo šta se nalazi u zatvorenoj kutiji i kako se ona ponaša. Ponašanje modela se istražuje delovanjem na taj model i proučavanjem reakcija na ta delovanja. Model crne kutije se koristi za istraživanje nepoznatih ili vrlo složenih dinamičkih sistema. Model crne kutije se koristi prilikom konstruisanja novih proizvoda, pri tome se polazi od nepoznatog realnog sistema, crne kutije. Cilj istraživanja na modelu crne kutije jeste da se jasno i precizno definišu način funkcionisanja, zakonitosti ponašanja i strukturna građa tog realnog sistema, odnosno da se izvrši transformacija modela crne kutije (proučavanog realnog sistema) u model bele kutije. Slika 2.3. Grafički prikaz modela crne kutije Analogno pojmu model crne kutije uveden je pojam model bele kutije, kod koga su poznati zakoni ponašanja i procesi u njemu kao dinamičkom sistemu. Način funkcionisanja proučavanog sistema je u potpunosti poznat, komletno shvaćen i jasno prenesen na model bele kutije. U bilo kom modelu bele kutiji uvek ostaje nešto neobjašnjeno i nepoznato. Zbog toga se koristi model sive kutije. U praksi, većina realnih sistema se predstavlja modelom sive kutije. 2. Statički i dinamički modeli Statički (stacionarni) modeli se koriste za sisteme koji se ne menjaju, ili bar ne menjaju značajno tokom vremena. Ova vrsta modela se fokusira na procese ili sile koje održavaju sistem u stanju ravnoteže: Dinamički (nestacionarni) modeli, nasuprot tome, se koriste za sisteme koji se menjau tokom vremena, što je mnogo češći slučaj kod realnih sistema: 3. Modeli sa raspodeljenim parametrima i modeli sa grupisanim (nagomilanim) parametrima 21
23 Realni sistemi često pokazuju značajnu prostornu heterogenost kada su u pitanju njihovi elementi i procesi koji ih kontrolišu. Neki modeli uzimaju u obzir ove prostorne varijacije tokom matematičke formulacije. To se postiže deljenjem geografske oblasti, na koju se odnosi model, na određeni broj razdvojenih prostornih jedinica, kao što su poligoni, mreže ili nepravilno oblikovani prostorni objekti. Modeli koji dodeljuju različite vrednosti sistemskim parametrima i promenljivim posebno za svaku prostornu jedinicu se nazivaju modeli sa raspodeljenim parametrima. Međutim, ovaj pristup nije uvek moguć zbog računarskih ograničenja ili zbog nedostatka odgovarajućih prostornih podataka. U tom slučaju neophodno je dodeliti jednu, grupisanu vrednost za celu prostornu oblast modela. Takvi modeli se nazivaju modeli sa grupisanim parametrima Empirijski modeli Empirijski modeli se uglavnom zasnivaju na analizi rezultata eksperimenata. U empirijskim modelima se veze između ulaznih i izlaznih veličina postavljaju na osnovu rezultata merenja u eksperimenima. U eksperimentima se najčešće menjaju odabrane (značajne) ulazne veličine, a mere se izlazne veličine. Oblik svake od tih veza se definiše matematičkom funkcijom. Odluka o tome koje će se matematičke funkcije koristiti je obično kompromis između toga koliko dobro se određene funkcije uklapaju u postojeće podatke i relativne jednostavnosti njihovih matematičkih oblika. Empirijski modeli su često veoma korisni kada se donose neka predviđanja vezana za konkretan slučaj za koji je model razvijen. Ranije su se ovi modeli više koristili, ali sa napretkom teorijskih istraživanja i razvojem računara se sve manje koriste. Empirijski modeli se najčešće ne zasnovaju na teorijskoj analizi. Zbog toga emirijskim modelima često nedostaje dovoljno opštosti, pa se ne mogu primeniti za neke druge situacije sa sličnom problematikom. Kada su potrebni širi i opštiji modeli, onda se ti modeli zasnivaju na teoriji (a ne na eksperimentima) i nazivaju se teorijski modeli Prednosti empirijskih modela Složeni realni sistemi se često ne mogu opisati teorijski, ili se deterministički (fundamentalni) modeli ne mogu rešiti, pa empirijski modeli omogućavaju da se predvidi ponašanje tih sistema. Empirijski modeli se mogu koristiti sa relativno velikom pouzdanošću predviđanja ako se predviđa ponašanje istog ili sličnog sistema u opsegu vrednosti parametara za koje je predhodno izvršena analiza i razvoj modela. Najčešće su jednostavni za upotrebu (rešavanje) Nedostaci empirijskih modela Nedostaci empirijskih modela su: ne doprinese boljem razumevanju realnih sistema, jer se ne zasnivaju na teoriji (model crne kutije); postoji mogućnost da se neki od značajnih parametara ne uključi u analizu, pošto nisu zasnovani na teoriji; primena im je ograničena samo na slične sisteme i na opseg parametara kojii je korišćen prilikom izrade modela; ekstrapolacija pri primeni empirijskog modela nije dozvoljena! Na slici je prikazan primer greške pri ekstrapolaciji. 22
24 Primeri upotrebe empirijskih modela Primeri upotrebe empirijskih modela su: Predviđanje fizičkih, hemijskih, termodinamičkih veličina za jedinjenja ili smeše u određenim uslovima. Predviđanja ponašanja realnih sistema u različitim uslovima. Kalibracija (baždarenje) instrumenata (uređaja) za merenje, analizu, monitoring itd Primer eksperimentalne identifikacije sistema Postavljanje empirijskih modela na osnovu dinamičkih eksperimenata u realnom (ili pilot) sistemu identifikacija dinamike procesa ili načina strujanja Teorija sličnosti Teorija sličnosti definiše matematičke odnose između fizički sličnih sistema različitih veličina. Predstavlja osnovu za uvećanje (smanjenje) razmera (scale-up) uređaja i procesa. Kriterijumi sličnosti se mogu definisati pomoću diferencijalnih jednačina ili pomoću dimenzione analize. Bezdimenzione grupe dobijene pomoću kriterijuma sličnosti predstavljaju osnovu za 23
25 izgradnju većine empirijskih korelacija. Kriterijumi sličnosti su: geometrijska sličnost, kinematička sličnost, termička sličnost i hemijska sličnost Dimenziona analiza Dimenzionom analizom se opisuje fizički sistem sa minimalno potrebnim brojem nezavisno promenjivih. Promenjive se grupišu u bezdimenzione grupe koje ne zavise od mernih jedinica. Određivanje tačnog broja relevantnih promenjivih je esencijalno - sistem se mora dobro poznavati. Primer: Pomoću dimenzione analize utvrditi koje su bezdimenzione grupe potrebne za korelisanje eksperimentalnih rezultata za prinudnu konvekciju u dugačkom cilindru. Rešenje: Problem je definisan sa bilansom količine kretanja i bilansom energije za diferencijalni element zapremine. Za pojednostavljenje usvajaju se pretpostavke: Uspostavljeno je stacionarno stanje i bilansi po x pravcu. Gravitacioni član i gradijent pritiska u bilansu KK se zanemaruju. Član generisanja toplote u energetskom bilansu je 0. Granični uslovi: u 0 =u, q 0 = h T Pod datim pretpostavkama diferencijalne jednačine modela: Promenjive i konstante n=7: Osnovne jedinice m = 4: Broj bezdimenzionih grupa: n m = Empirijske korelacije Za predviđanje veličina (koeficijenata) pod različitim uslovima često se koriste empirijske korelacije. Korelacije su najčešće bezdimenzione, oblika stepene funkcije:, npr.: 24
26 Izbor bezdimenzionih grupa se vrši na različite načine: teorijskom analizom, teorijom sličnosti, eksperimentalnom opservacijom i iskustvom itd. Koeficijenti i stepeni u korelacijama se dobijaju na osnovu većeg broja eksperimentalnih rezultata. Empirijske korelacije dobijene regresijom eksperimentalnih podataka Korelacije linearna i nelinearna regresija Koeficijenti u korelacijama se često dobijaju metodom najmanjih kvadrata linearna i nelinearna regresija eksperimentalnih rezultata. Linearna zavisnost: gde su: x 1, x 2 i x 3 - vektori promenjivih (parametara) y - vektor veličine koja se koreliše Jednačina (1) se može predstaviti u matričnom obliku: gde je: X - matrica: I - jedinični vektor Koeficijenti korelacije a 0, a 1, a 2,... se konačno mogu dobiti pomoću matrične operacije: ili gde je: y eks - vektor eksperimentalnih vrednosti Eksperimentalna validacija modela Matematički modeli se najpouzdanije provravaju pomoću eksperimentalnih rezultata. Poređenje rezultata modela sa rezultatima eksperimenta se vrši grafički ili tabelarno. Izračunata greška modela u odnosu na eksperimente kvantitativno određuje kvalitet modela i verifikuje ga. Pre poređenja neophodno je usaglasiti veličine dobijene modelom sa onim iz eksperimenata! 25
27 Interpretacija greške zavisi od ciljeva modelovanja, sistema koji se modeluje i metoda rešavanja. Greške empirijskih modela Srednja apsolutna greška: Srednja relativna greška: Suma kvadrata odstupanja: Srednje kvadratno odstupanje: 4.2. Deterministički (fundamentalni) modeli Deterministički modeli su modeli čije se ponašanje može predvideti, tj. novo stanje je potpuno određeno prethodnim. Deterministički model je model čiji su rezultati jedinstveni i određeni inputima (ulaznim parametrima). Ovakvi modeli uvek funkcionišu na isti način i uvek daju potpuno iste rezultate za iste zadate vrednosti inputa. Deterministički modeli su obično zasnovani na pretpostavkama, teoriji ili znanju o prirodi i oblužilu veza između ključnih elemenata proučavanog sistema. Deterministički (fundamentalni) modeli se zasnivaju na osnovnim zakonima fizike i hemije, kao što su: bilansi materije, energije, količine kretanja; brzina hemijske reakcije; brzina prenosa mase i toplote itd. 26
28 Bilansi se postavljanju na različitim dimenzionim skalama, u zavisnosti od veličine sistema i/ili željenog nivoa detaljnosti opisa. Deterministički modeli se matematički opisuju pomoću diferencijalnih (običnih i parcijalnih) i algebarskih jednačina na osnovu bilansa i brzine procesa Prednosti determinističkih (fundamentalnih) modela Prednosti determinističkih (fundamentalnih) modela su: mogu da doprinesu boljem razumevanju realnih sistema (pojava), jer teorijski opisuju te realne sisteme; pomoću njih se može predvideti ponašanje realnih sistema u različitim uslovima, mogu se koriste se za projektovanje uređaja i upravljanje procesima; njihovom primenom se smanjuje ili eliminiše potreba za izgradnjom pilot uređaja; mogu pomoći prilikom planiranja eksperimenata i smanjenju broja eksperimenata; Nedostaci determinističkih modela Nedostaci determinističkih (fundamentalnih) modela su: realni sistem koji se modeluju moraju se vrlo dobro poznavati pre izrade modela, što zahteva raznovrsna i specifična znanja i veštine inženjera (istraživača); ponekad izrađeni modeli mogu biti vrlo složeni pa se ili ne mogu rešiti postojećim metodama ili je potrebno mnogo (računarskog) vremena i resursa. Napomena: Modele, čak iako su vrlo detaljni (precizni), je neophodno verifikovati poređenjem sa eksperimentima, pre verifikacije se modeli ne mogu upotrebljavati sa dovoljnom pouzdanošću Primeri upotrebe determinističkih (fundamentalnih) modela Deterministički (fundamentalni) modeli se upotrebljavaju za: Predviđanje profila brzina u reaktoru sa pregradama u cilju optimalnog dizajna uređaja po pitanju pada pritiska. Korišćenje matematičkih modela u prediktivnom upravljanju u cilju smanjenja potrošnje pare u destilacionoj koloni Nivoi matematičkog opisa sistema i procesa Postoje četiri nivoa matematičkog opisa sistema i procesa: Mikroskopski nivo opisa, se upotrebljava za: o molekulski nivo, o hemijsku kinetiku, o molekulsku termodinamiku, o kvantnu mehaniku. Mezoskopski nivo opisa, se upotrebljava za: 27
29 o opis strujanja na nivou vrtloga (turbulencija), o prenos mase i toplote na nivou čestice. Makroskopski nivo opisa, se upotrebljava za: o režime strujanja, o operacije i uređaje, o procese i postrojenja Megaskopski nivo opisa, se upotrebljava za: o Planiranje proizvodnje i lanca nabavke za više fabrika. o Analizu uticaja proizvoda na životnu sredinu tokom njegovog životnog ciklusa. o Procenu uticaja novih projekata na životnu sredinu. o Predviđanje scenarija zagađenja i disperzije štetnih materija u životnu sredinu. Kod megaskopskog nivoa opisa, nivo opisa je širi od procesa i postrojenja, osim tehničkotehnoloških, uključuje društvene aspekte: ekonomske, pravne, zaštitu životne sredine itd. Modeli su složeni, sadrže navedene aspekte, pa zavise od razvoja i potreba datog društva i njihovih normativnih akata (ali nisu detaljni po pitanju fizičkih i hemijskih pojava) Populacioni modeli Populacioni modeli se koriste za opisivanje ponašanja populacije elemenata (čestica) i njihovog okruženja na osnovu ponašanja pojedinačnog elementa u njegovom lokalnom okruženju. Koriste se u različitim naučnim disciplinama, kao što su: hemijsko inženjerstvo, astrofizika, biologija, geofizika itd. Populacioni modeli u hemijskom inženjerstvu se koristi za opisivanje realnog proticanja u sudovima, jer se detaljni fundamentalni (mezoskopski, CFD) modeli teže rešavaju u dužem vremenskom periodu. Populaciono bilansni modeli koriste funkcije verovatnoće (raspodele, gustine raspodele), eksperimentalne rezultate i teorijske osnove iz fizike, predstavljaju kombinaciju stohastičkog, empirijskog i fundamentalnog pristupa. Prvi je funkcije raspodele vremena boravka fluida u sudu definisao hemijski inženjer Danckwerts. Raspodela starosti fluida koji napušta sud E(t) Funkcija verovatnoće, gustina raspodele: E(t) jedinice: 28
30 U bezdimenzionom obliku, za bezdimenziono vreme: Raspodela vremena zadržavanja fluida F(t) Verovatnoća da element fluida na izlazu ima vreme zadržavanja manje od t: Dobija se sabiranjem svih udela na izlazu u vremenu između 0 i t Stohastički modeli Stohastički modeli se koriste za opisivanje realnih sistema u kojima se veličine menjaju nepredvidljivo, odnosno slučajno. Koriste se za opisivanje procesa u kojima se veličine na izlazu (i/ili posle određenog vremena) ne mogu jednoznačno odrediti na osnovu stanja sistema na ulazu (ili u predhodnom (početnom) trenutku), tj. izlazne veličine nisu jednoznačno određene ulazom. 29
31 Stohastički modeli su modeli čije se ponašanje ne može unapred predvideti, ali se mogu predvideti verovatnoće promena stanja. Za stohastičke modele je karakteristično slučajno ponašanje, postojanje slučajnih promenljivih. Ovaki modeli se mogu koristiti za predstavljanje procesa igara na sreću, ili nekih sportskih simulacija kao što su košarka ili tenis. Stohastički modeli se koriste kada realni sistemi (procesi) imaju složenu unutrašnju strukturu koja se ne može analitički (deterministički) opisati. Stohastički modeli predviđaju ishod slučajnih procesa, ali sa izvesnom neodređenošću, koja se opisuje raspodelom verovatnoće - zasnovani su na teoriji i zakonitostima verovatnoće I statistike. Nasuprot determinističkom, stohastički model je model kod koga slučajni događaji i efekti imaju značajnu ulogu. Kod ovakvih modela promenljive koje se koriste nemaju jednu vrednost već se one opisuju uz pomoć raspodele (distribucije) verovatnoće. Ishod toga je da će rezultat ovakvog modela varirati od simulacije do simulacije, iako su početne vrednosti ulaza (imputa) uvek iste. Ova vrsta modela je pogodna za primenu kada postoje očigledne slučajne fluktuacije u proučavanom sistemu. Ove fluktuacije mogu biti posledica nekih prirodnih procesa koji su po svojoj prirodi slučajni ili mogu biti pseudo-slučajni, što znači da je naše znanje o nekom procesu nedovoljno ili neadekvatno, pa ne možemo uočiti uzročno-posledične veze, i iz tog razloga ga tretiramo kao slučajni proces. Kontinualne i diskretne funkcije Kontinualne funkcije, kontinualne promenjive mogu uzeti bilo koju vrednost unutar inervala. Primeri: brzina kretanja čestice, temperaturni profil u reaktoru, gustina smeše itd. Diskretne funkcije, diskretne promenjive mogu uzeti samo jednu različitu vrednost u intervalu (polju). Primeri: dnevne temperature u mesecu, uzorci fluida za merenje koncentracije itd. Slučajna veličina i stohastički procesi 30
32 Slučajna veličina X, ako se pri ponovljenim merenjima najčešće dobijaju različite vrednosti date veličine. Familija vremenskih funkcija slučajnih veličina 1 (t), 2 (t), 3 (t),... predstavlja stohastički proces. Osnovne karakteristike stohastičkih veličina i procesa su: srednja vrednost, varijansa (disperzija), autokorelaciona funkcija i uzajamna korelaciona funkcija, stacionarnost itd. Primeri slučajnih veličina i procesa: mikroskopski nivo: rast kristala, oblik i rast prskotine u materijalu, rast ćelija u tkivu, emisija elektrona sa katode, kretanje i sudari molekula gasa, mezoskopski nivo: kretanje čestica pri transportu, raspored čestica katalizatora pri nasipanju u kolonu, makroskopski nivo: vreme rada uređaja do kvara, vreme remonta, šum izmerene veličine. Raspodela verovatnoće slučajne promenjive X(t) Svojstva raspodele: Gustina raspodele verovatnoće veličine X(t) 31
33 Svojstvo gustine: Drugi red: Srednja vrednost i varijansa Srednja vrednost slučajne veličine (matematičko očekivanje ): Srednja vrednost definiše položaj centra slučajne veličine. Srednja vrednost stohastičkog procesa: Svojstvo aditivnosti srednje vrednosti: Srednja vrednost = prvi moment. Varijansa slučajne veličine (rasipanje, disperzija) oko srednje vrednosti: Dve slučajne veličine ili dva procesa mogu imati istu srednju vrednost, a različitu varijansu. Varijansa stohastičkog procesa: Varijansa = drugi centralni Primer: Na ispitu iz predmeta Modelovanje i simulacija procesa raspored broja studenata po intervalu osvojenih poena je dat u tabeli. Izračunati srednju vrednost i varijansu (disperziju) za rezultate ispita. 32
34 Srednja vrednost poena: Varijansa: Autokorelaciona funkcija, predstavlja zavisnost X(t) u vremenu t 1 od vrednosti u drugom vremenu t 2 : Autokorelaciona funkcija pokazuje da li se X(t) menja brzo ili sporo. Autokorelaciona funkcija za stohastički proces: Y(t): Uzajamna korelaciona funkcija, predstavlja zavisnost jedne slučajne veličine X(t) od druge Uzajamna korelaciona funkcija pokazuje koliko su dve stohastičke funkcije zavisne. Uzajamna korelaciona funkcija za stohastički proces: Stacionarnost i ergodičnost stohastičkih procesa Stohastički proces je stacionaran ako su raspodele verovatnoće identične: 33
35 Stacionarnost u širem smislu (slaba stacionarnost) ako: - ne zavisi od t, 2 ne zavisi od t r ( ) r ( ) su funkcije jedne promenjive (dužine vremenskog intervala). Stacionaran stohastički proces je ergodičan ako prosečne vrednosti dobijene na osnovu jednog niza opažanja mogu da se smatraju aproksimacijama prosečnih vrednosti procesa u celini (svaka realizacija ili uzorak nosi tipične, zajedničke osobine za ceo proces). i 2 procesa se mogu odrediti na osnovu jednog uzorka. Markov-ljev lanac Pojam Markovljev lanac se koristi za diskretna stanja, dok se pojam Markov-ljev proces koristi za kontinualne promenjive. Markov-ljev lanac: stanje slučajne veličine (ili procesa) u budućem vremenu zavisi samo od stanja u sadašnjem vremenu, a ne od stanja u prošlim vremenima: Pri svakom koraku, sistem može da se promeni u novo stanje ili da ostane u trenutnom stanju, po određenoj raspodeli verovatnoće verovantnoća tranzicije. Primer Markov-ljevog lanca: slučajno kretanje (random walk) - prostor stanja je dijagram; u jednom tranzicionom koraku verovatnoća kretanja od datog elementa ka bilo kom susednom elementu je jednaka, bez obzira na istoriju kretanja. itd. Primene modela slučajnog kretanja: U fizici: Brown-ovo kretanje, kretanje molekula u gasu ili tečnosti, agregacija čestica itd. U hemiji: opis polimernog lanca (3D ili 2D model). U biologiji: kretanje populacije životinja, genetička varijabilnost itd. U informacionim tehnologijama: procena veličine interneta itd. U ekonomiji: modelovanje cena deonica, modelovanje kockanja itd. Modelovanje diskretnih raspodela Binomna raspodela se koristi kod uzimanja uzoraka u eksperimentima, provere obrazaca Uslovi: postoji utvrđen broj ishoda n, ishod je ili povoljan ili nepovoljan, verovatnoća povoljnog ishoda p, a nepovoljnog (1-p), eksperimenti nezavisni. Funkcija raspodele verovatnoće: Srednja vrednost: 34
36 Varijansa: Poisson-ova raspodela se koristi kod radioaktivnog raspada, procesa čekanja i dolazaka, komunikacionih mreža itd. Uslovi: događaji nezavisni i retki. Funkcija raspodele verovatnoće: Srednja vrednost: Varijansa: Primer: Izveštaji iz fabrike pokazuju da se na svakih proizvoda javlja 25 neispravnih. Kolika je verovatnoća da će 1000 proizvoda sadržati najviše 3 defektna? Rešenje: U pitanju je diskretna raspodela. Pošto je frekvencija pojavljivanja neispravnih proizvoda mala, možemo koristiti Poisson-ovu raspodelu: Verovatnoća pojave defekta: Broj ishoda: Ukupna verovatnoća za tri neispravna proizvoda jednaka je zbiru verovatnoća: Koristeći Poisson-ovu raspodelu dobija se: Polinomna raspodela se koristi kod uzimanja uzorka, opšta binomna raspodela. Verovatnoća prvog ishoda x 1 je p 1, verovatnoća drugog ishoda x 2 je p 2 itd., pri čemu je p 1 + p p k = 1. Uslov: svaki eksperiment nezavisan, verovatnoća svakog ishoda konstantna i predstavlja broj kombinacija c(n, x). Funkcija raspodele verovatnoće: Srednja vrednost: 35
37 Varijansa: Hipergeometrijska raspodela se koristi kod uzimanja probe bez povraćaja - detekcija defektnog uzorka. Modelovanje kontinualnih raspodela Normalna (Gauss-ova) raspodela se koristi za opisivanje greške merenja. Gustina normalne raspodele verovatnoće: Ako se uvede smena za normiranu veličinu u: Gustina normirane raspodele: Funkcija normirane raspodele: Srednja vrednost normirane raspodele: Varijansa normirane raspodele: Funkcija normirane normalne raspodele P(u) se može dobiti numeričkom integracijom, rešavanjem tzv. Laplaceove funkcije, odnosno integrala: 36
38 rešenja ovog integrala za x > 0 se mogu naći u tablicama, dok za x < 0 važi: jer je neparna f-ja. (-x) = - (x) Shodno pravilu 3, verovatnoća za slučajnu promenjivu x, sa srednjom vrednošću x i varijansom x, u intervalu a < x < b se računa: Primer: Za određivanje gustine trokomponentne smeše izveden je veliki broj eksperimenata. Utvrđeno je da se greška merenja (slučajna veličina x) može prikazati pomoću normalne raspodele, a da je srednja vrednost greške 5 promila, a varijansa 1. Kolika je verovatnoća da će greška merenja gustine smeše imati vrednost u intervalu od 4 do 7? Rešenje: Primenom predhodne jednačine, za x = 5 i x = 1, dobija se: Pri rešavanju se koristi svojstvo neparnosti Laplace-ove funkcije (-x) = - (x). Rešenje je dobijeno pomoću tablica za (2) i (1). Logaritamska normalna raspodela, se koristi kod modelovanja raspodele veličina čestica (kondenzacija, aerosoli, granulometrija itd.). Primenjuje se kada nekoliko nezavisnih faktora utiče na ishod događaja. Gustina logaritamske normalne raspodele verovatnoće: gde je: Srednja vrednost: Varijansa: Ostale raspodele su: gama, eksponecijalna, beta, 37
39 Hi-kvadrat itd Primena Monte Karlo metode u modelovanju stohastičkih procesa Monte Karlo metoda koristi slučajne veličine kako bi se opisalo ponašanje sistema koje je toliko složeno da se ne može tačno opisati pomoću klasičnih determinističkih modela. Monte Karlo metoda se zasniva na generisanju slučajnih veličina i iterativnim postupcima - za proračune se koriste računari. Problem se, pomoću Monte Karlo metode, rešava tako što se repetativno generišu slučajni brojevi i posmatra se raspodela udela brojeva koji se pokoravaju određenom pravilu ili skupu pravila. Metoda je tačnija što su brojevi uniformnije raspoređeni u polju od interesa i što se više puta postupak ponavlja. Postoji veći broj algoritama za Monte Karlo metodu, često se primenjuje Metropolis- Hastings-ov algoritam. Monte Karlo metoda je opšteg karaktera i danas se primenjuje za najrazličitije proračune u prirodnim, tehničkim i društvenim naukama. Osnovne oblasti stohastičkih proračuna gde se tradicionalno primenjuje Monte Karlo metoda: numerička integracija za višedimenzione integrale u matematici; simulacija slučajnog kretanja u statističkoj mehanici i fizici; praćenju kretanja čestica i radioaktivnosti; fizičko-hemijski fenomeni i procesi, biološko-medicinske pojave: epidemije virusa i bakterija, rast populacije, migracije insekata i ptica, širenje radioaktivnosti i tumora u organizmu, geološko-sredinske pojave i procesi: erozija tla, širenje požara, klimatske promene, disperzije polutanata; optimizacija i dinamičke simulacije: nabavka sirovina, transport ljudi i proizvoda; finasije i ekonomija: procena vrednosti firmi, rast tržišta i berze, kvote osiguranja; matematika; razvoj software i zabavne igre. Opšti algoritam Monte Karlo metode: 1. Definisanje domena. 2. Generisanje slučajnih vrednosti u domenu. 3. Izvršavanje determinističkog proračuna koristeći slučajne vrednosti. 4. Uvrštavanje rezultata pojedinačnih proračuna u ukupan rezultat. Jednostavan opis principa igra podmornice A Slučajni brojevi: Prvo igrač slučajno gađa u polje bitke. B Primena pravila: Na osnovu pogotka, igrač postavlja mogući raspored podmornica od četiri tačke. 38
40 C Zaključak: Na osnovu slučajnih gađanja i primene pravila igrač donosi zaključak o položaju podmornice protivnika. Primer upotrebe Monte Karlo metode za simulaciju Efekta staklene bašte (klimatskih promena) primenom aplikacije NetLogo Stohastička simulacija uticaja koncentracije CO 2 i količine oblaka na temperaturu atmosfere. Oblaci blokiraju sunčeve zrake, a CO 2 blokira emisiju infracrvenih zraka sa zemlje izazivajući efekat staklene bašte. 39
41 5. STATISTIČКA ISTRAŽIVANJA Statistika se prvobitno odnosila samo na numeričke podatke o stanju posmatrane pojave. Osnovni zadatak statističkih istraživanja svodio se u početku na prikupljanje podataka o brojnom stanju stanovnika, vojnika, poreskih obveznika, imovine jer su tadašnji vladari želeli da znaju kolika je njihova i vojna moć u odnosu na svoje protivnike. Prvi popis stanovništva prema nekim podacima bio u Egiptu godina p.n.e. U početku su razvijena dva pristupa obradi podataka. Prema prvom pristupu akcenat je bio stavljen na to da je zadatak statistike, sistematizacija podataka o stanovništvu i privredi u cilju vođenja državne politike, bez pretenzija na otkrivanje zakonitosti. Zadatak drugog pristupa prema statistici bio je fokusiran na matematičku obradu statistički podataka i otkivanje zakonitosti u ponašanju posmatranih pojava, čime su postavljeni temelji razvoja savremene statistike. Nagli napredak u statistici osetio se pronalaskom i razvojem računara. Izuzetno brza i pouzdana obrada podataka skratila je vreme izračunavanja statističara umnogome nekoliko puta. Danas se razlikuje: teorijska i primenjena statistika. Teorijska (matematička) statistika pronalazi nove statističke metode, objašnjava ih, dokazuje i usavršava. Ona se može smatrati delom primenjene matematike. Primenjena statistika podrazumeva statističke metode prikupljanja, obrade i analize podataka, kao i donošenje zaključaka i formulisanje zakonitosti ponašanja posmatranih pojmova. Primenjena statistika može se podeliti u dve gupe: deskriptivnu i inferencijalnu statistiku. Deskriptivna statistika obuhvata prikupljanje i obradu podataka i njihovo prikazivanje u obliku tabela, grafikona i sumarnih deskriptivnih mera. Njan domen je ograničen samo na raspoložive podatke. Inferencijalna statistika podrazumeva primenu statističkih metoda (kreiranih u okviru teorijske statistike) koji nam omogućavaju da zaključke o pojavi koja se ispoljava na velikom broju sličajeva (u skupu) donesemo samo na odnovu jednog dela podataka (dela skupa). Stoga je njen domen znatno širi od deskriptivne statistike. Zaključci dobijeni primenom metoda inferencijalne statistike baziraju se na rezultatima teorijske statistike i teorije verovatnoće. Teorijska statistika se može smatrati delom primenjene matematike, dok je primenjena statistika naučna oblast koja se bavi analizim podataka. Кako bi se predmet statistike lakše shavatio uveden je pojam varijabilana pojava. Varijabilitet (odnosno raznovrsnost, raznolikost) je univerzalno prisutan oko nas. Primer za varijabilitet su privredna društva (firme) u Republici Srbiji, one se razlikuju po broju zaposlenih, delatnosti, lokaciji, brojem pokazatelja uspešnosti poslovanja, da li su i na koji način prisutni na Internetu itd. Varijabilna pojava je ona koja uzima različite vrednosti od jednog do drugog slučaja svoga ispoljavanja. Na varijabilnu pojavu često deluje veći broj faktora ( čije individualne i 40
42 združene uticaje nije moguće unapred odrediti), zbog čega se i pojedinačne vrednosti varijabilne pojave ne mogu sa sugurnošću predvideti. Iz gore navedene dofinicije može se zaključiti da 2000 litara destilovane vode nije varijabilna pojava jer su jedinice iz kojih se ona sastoji identične. Ovakve, apsolutno homogene pojave ne zanimaju statistiku. Varijabilnost neke pojave nema nikakve veze sa brojem slučajeva (masovnošću) na kojima se ta pojava iskazuje. S druge stane posmatrajući grupu on npr. pedeset studenata, može se zaključiti da postoji varijabilna pojava. Jer posmatrana grupa studenata pokazuje varijacije po visini. Takođe ako bismo u obzir uzeli jednog studenta, ne bi bilo moguće unapred utvrditi visinu jer ne postoji varijabilna pojava na jednom primerku. Recimo, u medicini bez izučavanja varijacija bilo bi skoro nemoguće postaviti dijagnozu. Ovde se polazi od vrednosti indikatora zdravih osoba koje se smatraju referentnim (normalnim), a zatim se definišu dozvoljena odstupanja od te normale, kao i ona koja sa sugurnošću ukazuju na postojanje problema. U ekonomiji pri što boljem pozicioniranju na tržištu proizvodna firma mora da prati brojne indikatore sa tržišta i shodno varijacijama pojedinih pokazatelja menja svoju proizvodnu ili prodajnu strategiju. Generalno, skoro u svim naučnim disciplinama varijacije posmatranih pojava se analiziraju, pomoću posebnog metodološkog aparata. Na osnovu toga što je rečeno može se zaključiti da je statistika neizostavna po pitanju zanačajnosti u ekonomiji. Da bi se došlo do odrećenih zaključaka i donošenja nekih hipoteza mora se proći kroz niz postupaka koji su zastupljeni u obradi statističkih podataka. Pitanje koje se često postavlja vezano za statistiku jeste to kako se statistika suočava sa podacima u realnosti i sa njihovom varijabilnošću. S obzirom na to da se statistika definiše kao nauka o podacima (podaci su brojevi ili reči sa odgovarajućim kontekstom). Statistika se pre svega bavi globalnim podacima, dok oni pojedinačni ostaju anonimni. Ako se pokaže da neki podaci previše odstupaju od ostalih prema današnjem shvatanju statistike i oni spadaju u predmet interesovanja za statistiku. Takvi podaci se danas nazivaju ekstremnim podacima (eng. outliers). Ekstremni podatak je onaj podatak koji znatno odstupa od vrednosti svih ostalih podataka, bilo zato što je veći ili znatno manji. Nekada se smatralo da ekstremna vrednost nastaje kao greška u merenjima ili unosu podataka. Međutim, ekstremna vrednost može biti i signal da se nešto neuobičajeno događa sa posmatranom pojavom. Tipičan primer za to je otkrivanje ozonskih rupa trebalo je da prođe nekoliko godina da bi ekstremni podaci, koje je kompjuterski softver instaliran u satelitima ignorisao, istraživačima ukazali da se nešto novo događa sa atmosferom iznad Antarktika. Značaj ekstremnih podataka je toliko veliki da se posebna grana statistike bavi isključivo njome (Extremevaluetheory). Statistika je veoma osetljiva na netačne ili nepotpune podatke, koji se koriste pri analiziranju, na osnovu statističkih analiza moguće je otkriti neku pravilnost ili nepravilnost koja bi bez njene pomoći bila gotovo nemoguća. Primer koji se sreće često u domaćim, a pogotovu u stranim literaturama je: Očekivano trajanje života kod muškaraca i žena. Prema podacima objavljenim od strane Ujedinjenih nacija za period od 2005 do godine prikazani su u tabeli 1. 41
43 Tabela 1. Očekivano trajanje života živorođenih u periodu od 2005 do za najrazvijenije, najnerazvijenije zemlje na svetu i Republiku Srbiju Muškarci Žene Oba pola Najnerazvijenije zemlje 53,4 55,8 54,6 Najrazvijenije zemlje 72,9 80,2 76,5 Republika Srbije 71,7 76,3 74,0 Prema gore navedenim podacima, može se sa sigurnošću utvrditi da žene žive duže od muškaraca. Кada se ide još dalje u razmatranje ovog pitanja dođe se do podatka da se devojčice ipak ređe rađaju od dečaka. Prema nekim podacima na 100 devojčica rodi se 106 dečaka. Ove pojave nazivaju se statističkim zakonitostima. Oni se mogu podeliti na dve bitne karakteristike: Važe samo u masi slučajeva; Pojedinačni slučajevi mogu da pokažu odstupanja od opšte tendencije. Statističke zakonitosti ograničenja. moramo tumačiti strogo vodeći računa o navedena dva U primeru sa očekivanim trajanjima života, zakonitost tumačimo da žene žive duže od muškaraca, a nikako da svaka žene živi duže od muškarca, pa se može na osnovu ovoga zaključiti da neće svako dete u Srbiji, rođeno posle godine, živeti do 76,3. godine. Zanimljiv je podatak da su stari Grci procenjivali da je prosečan životni vek biti oko 28 godina. Verovatno se uzimalo u obzir to što je postojala velika opasnost po život usled čestog ratovalja, bolesti i gladi. Međutim, Sokrat je živeo 70, Platon 80, a Aristotel 62. godine Primena računara u statističkoj analizi Otkriće računara sredinom XX veka donosi sa sobom potpuno novu dimenziju u svere obrade podataka, analizu podataka itd. Značajni napredak koji se dogodio u proteklih dvadeset godina imao je za posledicu razvoj aplikacija na računare koji su sposobni da potpuno samostalno izvršavaju složene statističke proračune kao i druge funkcije bitne za statistiku, a pritom sve te funkcije obavljaju se izuzetno brzo i pouzdano. U današnje vreme posredstvom odgovarajućih programa veoma jednostavno se obavljaju varijabilne projave. Više nema potrebe za ručnim izračunavanjem koje je uvek praćeno manjim ili većim greškama. Danas postoji veliki broj programskih paketa koji su veoma korisni u analizi statističkih podataka. Neki od njih su: SPSS, Minitab, SAS, Statgraphics, S Plus, JMP, SATA itd. Statističari su formulisali i posebne programske jezike od kojih je najpoznatiji jezik koji se naziva R i koji može da se skine potpuno besplatno sa interneta Statistički skup Predmet statističkog istrživanja su varijabilne pojave. Da bi se tačno sagledale pravilnosti u njegovom ponašanju neophodno je obuhvatiti sve slučajeve na kojima se ona pojavljuje. Iz tog razloga dolazi se do termina statistički skup. Skup svih elemenata na kojima se izvesna varijabilna pojava ispoljava i statistički posmatra naziva se statističkim skupom ili osnovni skup ili, jednostavno, skup. 42
44 Na osnovu definicije je jasno da neki skup mora ispunjavati određene uslove da bi mogao da se nazove statističkim skupom. Statistički skup mora da obuhvati sve elemente koju su predmet posmatranja; Elementi tog skupa moraju imati bar jednu zajedničku osobinu na osnovu koje se i deklarišu kao pripadnici toga supa; Na elementima takvog skupa se posmatra neka varijabilna pojava. Iz ovoga sledi da ti elementi moraju imati bar jednu karakterisiku po kojoj se mogu razlikovati, odnosno koja je varijabilna. U zavisnosti od cilja istraživanja, osnovni skup se može sastojati od ljudi, bića, predmeta ili događaja. Tako na primer, satistički skup mogu činiti svi stanovnici grada ili zemlje, svi studenti fakulteta, ali i stočni fond u nekoj državi, sva preduzeća u jednom gradu ili pokrajini, itd. Sve jedinice nekog skupa analiziramo u izabranom momentu i određujemo strukturu skupa po izabranim karakteristikama. Jedinica skupa predstavlja pojedinačni element iz kojeg se skup sastoji. Može se još nazvati i jedinicom posmatranja. Može se zaključiti da sve jedinice osnovnog skupa moraju imati barem jednu zajedničku osobinu. Sa porastom broja jedinica skupa osnovni skup postaje homogeniji. Ipak, jedinice ne smeju biti među sobom identične jer tada one nisu predmet statističkog posmatranja. Predmet statističkog istraživanja su varijabilne pojave zbog čega pažnju usmeravamo samo na one karakteristike po kojima se jedinice skupa među sobom razlikuju. Jedinice koje se smatraju deo skupa u praksi obično nisu jednostavne. One pre svega zavise od cilja i domena istaživanja. Zbog toga je potrebno da statistički skup precizno odredimo, definišemo: sadržinski, prostorno i vremenski. Sadržinski odrediti neki statistički skup zahteva jasno definisanje osobine koju mora da poseduje svaka jedinica da bi bila predmet posmatranja. Tako, na primer, skup mogu da čine svi studenti u državi, ali (u zavisnosti od cilja istraživanja), i uže grupe, kao što su svi studenti privatnih univerziteta, svi sudenti Viših fakulteta, svi studenti prve godine Višeg fakulteta, itd. Prostorno odrediti osnovni skup znači precizirati teritoriju u okviru koje će se posmatrati data varijabilna pojava. Posmatranja se najčešće sprovode na administrativnim jedinicama kao što su opštine, distrikti, republike ili države, a u nekim slučajevima ona obuhvata zajednice država (npr. Evropska unija), pojedine kontinente, pa i svet u celini. Vremenski odrediti skup znači precizno odrediti jedan momenat ili vremenski interval u kojem ćemo izmeriti nivo pojave. Snimanje pojave u trenutku ili u intervalu vremena zavisi od njene prirode, ali je veoma bitno precizno ih odrediti. Momenat u kojem se snima neki statistički skup je, po pravilu, određen potrebama istraživanja ili je propisan od strane zvaničnog statističkog organa. S druge strane, u cilju praćenja proizvidnje, i izvoza ili potrošnje moramo odrediti vremensko razdoblje, unutar koga ćemo vršiti kumuliranje podataka i tako odrediti vremenske pojave. Tako ćemo, u zavisnosti od potreba istraživanja, formirati dnevne, mesečne, kvartalne i godišnje podatke. 43
45 5.3. Statističko obeležje Jedinice osnovnog skupa se mogu među sobom razlikovati po brojevima karakteristikama, koje nas u konkretnom istraživanju mogu, ali ne moraju, sve interesovati. U zavisnosti od cilja istraživanja, pažnju po pravilu usmeravamo na jednu, dve ili veći broj ovakvih osobina. Takve karakteristike nazivamo statističkim obeležjima. Osobine po kojima se jedinice skupa među sobom razlikuju, a koje su predmet statističkog istraživanja, nazivamo obeležjima (promenljivim ili varijabilnim). Sva obeležja u statistici možemo klasifikovati u dve osnovne grupe: atributivna (kvalitativna, kategorijska) i numerička (kvantitativna). Atributivna obeležja se izražavaju opisno (rečima), a varijabilitet se ispoljava kroz pripadnost elemenata različitim kategorijama datog obeležja. Na primer, u statističkom skupu svih zaposlenih u JP Putevi Srbije, atributivna obeležja mogu biti: pol, školska sprema, boja kose ili očiju, itd. Statistika svih prodatih TAG uređaja za prolazak na naplatnim stanicama bez zaustavljanja u godini itd. Različiti vidovi u kojima se jedno obeležje može javiti nazivaju se modalitetima ili vrednostima tog obeležja. Broj modaliteta varira od prirode obeležja. Na primer, pol ima samo dva modaliteta: muški i ženski, kao i kvalitet proizvoda: isparavan i neispravan. Obeležje bračnog stanja ima četiri modaliteta: neoženjen neudata, oženjen udata, razveden razvedena, udovac udovica. Sa druge strane obeležja kao što su zanimanja, nacionalnost i šifra obavljanja delatnosti firme mogu imati veoma veliki broj različitih pojava oblika. Numerička obeležja su takve karakteristike skupa koje se mogu iskazati brojevima. Izdvajaju se dve karakteristične grupe: prekidna (ili diskretna) numerička obeležja, i neprekidna (ili kontinuirana) numerička obeležja. Suštinska razlika između ove dve grupe je u tome što prekidna obeležja svoje vrednosti (modalititete) dobijaju na osnovu prebrojavanja, a neprekidna na osnovu merenja. Prekidna se usled toga iskazuju celim brojevima, a neprekidna u mernim jedinicama. Prekidna obeležja su numeričke karakteristike koje mogu uzmati samo izolovane vrednosti na nekoj skali. Na osnovu toga se domaćinstva između sebe razlikuju po broju dece ili broju telefona, opštine se razlikuju prema broju stanovnika, kulturnih znamenja ili drugih stvari, fakulteti po broju studenata, studijskih programa itd. S obzirom na to da navedena obeležja imaju različite opsege i broj mogućih vrednosti, zajedničko im je ipak da njihovi modaliteti mogu biti samo celi brojevi. Neprekidna obeležja predstavljaju numeričke karakteristike jedinica skupa koje mogu uzeti bilo koju vrednost unutar nekog intervala. Ovoj grupi pripadaju, na primer, visina studenata, težina prizvoda, vreme dostavljanja pošiljke itd. S obzirom na to da svako merenje možemo preciznije izmeriti drugim i trećim merenjem. Može se zaključiti da svako neprekidno numeričko obeležje teorijski može imati beskonačno mnogo modaliteta. Iz dosada napisanog, obeležje predstavlja ono po čemu se jedinice skupa razlikuju, a ne ono po čemu su slične. Slika 2.4. prikazuje šemu pojma obeležja. 44
46 Sl Кlasifikacija obeležja (varijabli) u statistici 5.4. Statistički uzorak, reprezentativni uzorak i parametri skupa U prethodnim odeljcima pomenuto je da statistika ispituje varijabilne pojave na osnovu svih podataka statističkog skupa (metod popisa) ili na osnovu dela toga skupa uzorka. Statistički uzorak predstavlja deo statističkog skupa na osnovu čijih osobina donosimo statističke zaključke o odgovarajućim karakterima populacije iz koje je izabran. Važno je međutim napomenuti da uzorak nikada ne uzimamo da bismo saznali njegove karakteristike, već isključivo da bismo, uopštavanjem dobijenih informacija iz uzoraka, došli do informacije o nepoznatim karakterima skupa u celini. Da bi zaključci o karakteristikama celog statističkog skupa na osnovu samo jednog njegovog dela bili validni, neophodno je da uzorak bude reprezentativan. Uzorak je reprezentativan ako svojim osobinama verno oslikava osobine statističkog skupa iz kojeg je izabran. Uzorak, sam po sebi, nije cilj, već samo sredstvo da se dođe do željene informacije o skupu. Uzorak sa sobom nosi bitnu informaciju numeričkog karaktera. Takve informacije sveobuhvatno nose naziv parametri skupa. Parametri skupa predstavljaju sumirane karakteristike statističkog skupa. Na osnovu gore navedenog vidimo da je parametar neki broj koji se odnosi na skup. Prema svojoj statističkoj prirodi parametar je neka konstanta, a ne promenljiva. Jedini način da se neki parametar izračuna je putem popisa. Reprezentativni uzorak predstavlja, kao što je rečeno, deo osnovnog skupa prema kojem se može odrediti struktura osnovnog skupa, međutim u praksi gotovo nikada nema savršenog reprezentativnog uzorka, pa se na osnovu toga može zaključiti da će njegove vrednosti uvek pokazati menje ili veće oscilacije, odnosno, fluktacije naspram čitavog skupa. Cilj statističkog zaključivanja je da na osnovu statistike uzoraka dođemo do informacije o parametru skupa. Ovaj postupak prikazan je na slici
47 Sl Postupak statističkog zaključivanja 5.5. Prosta korelaciona i regresiona analiza U prethodnim poglavljima upoznali smo se sa metodama statističkog zaključivanja, odnosno kako se na osnovu informacije iz uzorka donose zaključci (putem ocenjivanja ili testiranja hipoteza) o nepoznatim karakteristikama osnovnog skupa. Sada ćemo naše interesovanje usmeriti na istraživanje međusobnih veza i uticaja dve ili više pojava. Tako, na primer, može nas interesovati da ispitamo zavisnost između vremena proveđenog u spremanju statistike i ocene na ispitu, dohotka i izdataka za kulturu domaćinstava, između zarada zaposlenih i godina školovanja, kamatne stope i ponude novca, izdataka za propagandu i prodaje, troškova za istraživanje i profita firme, broja kriminalnih dela sa jedne strane i stope nezaposlenosti i stope inflacije sa druge strane, itd. U svakom od navedenih slučajeva analizu sprovodimo pomoću dva, verovatno najpoznatija statistička metoda, korelacije i regresije. Kao i do sada, naše zaključivanje zasnivaće se na uzorku. Ali sada ćemo na osnovu uzorka ispitivati kako su varijacije jedne pojave (ili grupe od dve ili više pojava) povezane sa varijacijama neke druge pojave. Cilj našeg istraživanja neće se naravno odnositi na uzorak, već na osnovni skup iz koga je uzorak izvučen. U ekonomiji i društvenim naukama preovladavaju stohastičke veze između pojava. Dok kod funkcionalnih veza za svaku vrednost nezavisne promenljive X uvek postoji samo jedna vrednost zavisne promenljive Y, kod stohastičkih veza za jednu vrednost X postoji čitav niz mogućih vrednosti Y. Stohastičke veze u stvarnosti opisujemo pomoću stohastičkih modela. Ovi modeli uključuju slučajnu grešku kojom obuhvatamo uticaje svih faktora koje nismo uključili u model. Prilikom ispitivanja međuzavisnosti varijacija dve ili više promenljivih u statistici se primenjuju regresiona i korelaciona analiza. Ukoliko analiziramo samo dve pojave govorimo o prostoj regresiji ili korelaciji. U slučaju analize više od dve pojave, jednu od njih označavamo kao zavisno promenljivu i primenjujemo višestruku korelaciju ili regresiju. Pomoću korelacije ispitujemo da li između dve ili više pojava postoji kvantitativno slaganje, i ako postoji, kog je intenziteta. Pirsonov koeficijent se označava sa r i pokazuje da 46
48 li između dve numeričke promenljive u uzorku postoji linearna veza. Da bi se ispitalo da li i u osnovnom skupu postoji linearna veza njegovu vrednost moramo da testiramo pomoću Studentovog t testa. Pirsonov koeficijent spada u grupu parametarskih pokazatelja jer se zasniva na pretpostavci da je zajednički skup dve posmatrane promenljive normalan. Dok kod korelacije nije bitno koju smo promenljivu označili kao zavisnu a koju kao nezavisnu, kod regresione analize najpre mora da se izvrši identifikacija promenljivih. Cilj regresije je da se kroz ocenu parametara regresionog modela izvrši ocenjivanje prosečne vrednosti Y i predvide pojedinačne vrednosti Y. Zavisnost između dve pojave u prostoj linearnoj regresiji opisujemo kroz prost linearni regresioni model. Ukoliko su pretpostavke tog modela ispunjene tada metod najmanjih kvadrata, po Gaus-Markovljevoj teoremi, daje najbolje nepristrasne linearne ocene. Ideja metode najmanjih kvadrata kod proste linearne regresije je da se dođe do najbolje prave linije, odnosno one koja će najbolje reprezentovati vezu između dve pojave. To se postiže minimiziranjem sume kvadrata reziduala. Kod proste linearne regresije ocenjujemo dva parametra regresionog modela: odsečak i nagib. Ocenjena vrednost odsečka pokazuje ocenu prosečne vrednosti zavisne promenljive kada je objašnjavajuća promenljiva X jednaka 0. U praksi je daleko važnija ocena nagiba. Ona pokazuje ocenu prosečne promene Y kada se X poveća za svoju jedinicu. Da bismo sagledali da li regresioni model na zadovoljavajući način opisuje zavisnost dve pojave u realnosti koristimo dve mere reprezentativnosti. Prva je standardna greška regresije i ona je apsolutna mera, odnosno iskazana je u istim mernim jedinicama kao i Y. Druga mera se mnogo češće koristi i naziva koeficijentom determinacije. Ovaj koeficijent pokazuje udeo objašnjenog varijabiliteta u ukupnom. Dok koeficijent korelacije može uzimati vrednosti u intervalu [ 1, +1], koeficijent determinacije nikad ne može biti negativan. Njegova maksimalna vrednost je +1 i javlja se samo u slučaju da između dve pojave postoji funkcionalna veza, pa se sve empirijske tačke nalaze na pravoj liniji. Prilikom korišćenja regresionog modela u cilju predviđanja mora se voditi računa da je (a) koeficijent determinacije relativno visok, (b) da je ocena nagiba statistički značajna i (d) da nema prekomerne ekstrapolacije. Ekstrapolacija se javlja ako prilikom predviđanja Y uzimamo one vrednosti objašnjavajuće promenljive X koje su ili manje od minimalne ili veće od maksimalne u uzorku Funkcionalna i stohastička veza Međusobne veze između pojava (promenljivih) možemo podeliti u dve grupe: funkcionalne i stohastičke. Funkcionalna (deterministička, egzaktna) veza javlja u slučaju kada jednoj vrednosti nezavisne promenljive X odgovara samo jedna, tačno određena, vrednost zavisne promenljive Y. Tako, na primer, površina kvadrata izračunava se pomoću formule P = a 2. Za bilo koju željenu vrednost stranice kvadrata a, možemo egzaktno izračunati površinu P, jednostavnom zamenom numeričke vrednosti na desnoj strani jednakosti. Funkcionalne (determinističke) veze se retko sreću u društvenim naukama i ekonomiji. Posmatrajmo sada međuzavisnost dve ekonomske pojave, recimo, izdatke za propagandu (oglašavanje) računarske opreme (kao nezavisne promenljive) i prihod od prodaje te opreme (kao zavisne promenljive). Prvo pitanje koje se ovde postavlja je: da li postoji funkcionalna veza između ove dve pojave? Drugačije rečeno, da li na osnovu poznavanja izdataka za propagandu možemo egzaktno da predvidimo nivo prihoda od prodaje, na primer, u vidu relacije: 47
49 Prihod od prodaje = 5 Troškovi reklamiranja (1.11) koja bi važila za sve firme u Srbiji? To bi praktično značilo da ako neka firma uloži 1000 evra u reklamiranje, prihod od prodaje bi iznosio tačno 5000 evra. Složićemo se da je odgovor negativan i to iz više razloga. Prodaja računarske opreme ne zavisi samo od propagande, već i od niza drugih faktora, kao što su: cena opreme, cena konkurentskih proizvoda, dohotka potencijalnih kupaca itd. Čak i kad bismo u model uključili veliki broj faktora od kojih zavisi prodaja, ne bi bilo moguće predvideti egzaktnu vrednost prodaje. Zbog čega? Zbog toga što na pojave u društvu i ekonomiji deluju specifični nepredvidljivi uticaji psihološke prirode, kao i različiti slučajni uticaji. Zato nismo u stanju da na osnovu poznavanja pojedinih vrednosti nezavisne promenljive u potpunosti odredimo vrednosti zavisne promenljive. Ipak, očekujemo da postoji određena pozitivna veza između propagande i prodaje, u smislu: veći izdaci za propagandu veća prodaja. Ovakva veza je slabija od funkcionalne i naziva se stohastička 1 (eng. stochastical) veza. 1 Termin "stohastički" potiče od starogrčke reči στοχαστικός, što znači ciljati ili pogađati. Kod stohastičkih veza jednoj vrednosti nezavisne promenljive odgovara čitav niz mogućih vrednosti zavisne promenljive. U našoj formuli, odnosno modelu, (11.1), kod različitih firmi, za isti nivo izdataka za propagandu očekivali bismo različiti nivo prodaje. Drugim rečima, takav model ne samo da je suviše jednostavan, nego bi u praksi pokazivao manje ili veće greške. Kako onda da modeliramo veze između pojava u ekonomiji, koje su po svojoj prirodi stohastičke? Stohastičke veze između dve pojave modeliraćemo tako što ćemo u model, pored zavisne i nezavisne promenljive, uključiti još jednu komponentu, koja će obuhvatiti sve ostale faktore (osim X) koji utiču na Y. Bez uključivanja te komponente jasno je da bi naš model (11.1) za različite vrednosti X davao pogrešne vrednosti Y. Ta komponenta deluje na nepredvidljiv, slučajan način na Y. Kako da nazovemo tu komponentu koja na sasvim slučajan način dovodi do greške pri predviđanju u model (11.1)? Nazvaćemo je stohastički član ili slučajna greška modela, i već smo imali prilike da je upoznamo kod modela analize varijanse. Dakle, umesto relacije (11.1) međuzavisnost posmatrane dve pojave se neuporedivo bolje opisuje modelom Prihod od prodaje = 5 Izdaci za propagandu + Slučajna greška (11.2) Ovakav model dozvoljava da za razne vrednosti X imamo više različitih vrednosti Y. Generalno, stohastički model (generalna forma stohastičkog modela), odnosno veza, može se prikazati na sledeći način: Y = Deterministički član + stohastički član (11.3) Posmatranjem modela (11.3) nameće se logično pitanje: kako je uopšte moguće analizirati takav model, ako on uključuje potpuno nepredvidljivu komponentu, preciznije rečeno, slučajnu promenljivu? Statističari su pokazali da se takvi modeli ipak mogu koristiti tako što će se uvesti određene pretpostavke o stohastičkom članu modela. Za sada ukažimo samo na jednu od njih. Budući da stohastički član u različitim situacijama deluje na slučajan način, nekada tako što utiče pozitivno na Y, nekada negativno, pretpostavićemo da se ti uticaji u zbiru potiru, odnosno da je u proseku njegov uticaj jednak nuli. Kako je stohastički član, u stvari, slučajna promenljiva, koji statistički pokazatelj označava prosek te slučajne promenljive? Podsetimo se, to je, očekivana vrednost E(X). Dakle, E(stohastičkog člana) = 0. 48
50 Ako je u modelu (11.3) zavisna promenljiva Y funkcija stohastičkog člana, a ovaj je po svojoj prirodi slučajna promenljiva, koja je statistička priroda Y? Iz glave 4 znamo da je svaka funkcija slučajne promenljive i sama slučajna promenljiva. Zaključujemo stoga da je i Y slučajna promenljiva. Ostaje još samo da odredimo čemu je jednak prosek, tj. očekivana vrednost Y. Prosek Y, na osnovu relacije (11.3), biće jednak proseku zbira determinističkog i stohastičkog člana. Kako je prosek stohastičkog člana jednak nuli, zaključujemo da je: Prosek Y = Deterministički član. Da sumiramo: u ekonomiji stohastički model mnogo bolje opisuje realnost od determinističkog. On uvek u sebi uključuje bar jednu slučajnu promenljivu. Usled toga se u literaturi u poslednje vreme reči "stohastički" i "slučajni" shvataju kao sinonimi. Veze kod kojih porastû (opadanju) vrednosti nezavisne promenljive X istovremeno odgovara porast (opadanje) zavisne promenljive Y nazivamo direktnim vezama. Tipičan primer je odnos između primenjene količine određenog veštačkog đubriva i prinosa neke poljoprivredne kulture. Sa druge strane, ako porastû jedne promenljive odgovara opadanje druge, radi se o inverznim vezama (na primer, sa porastom cene avionskih karata opada broj putnika, uz konstantni realni dohodak). Naravno, ukoliko se ustanovi da sa promenama vrednosti jedne pojave druga promenljiva ostaje konstantna, zaključićemo da između njih ne postoji nikakva zavisnost. U stvarnosti, između dve ili više pojava moguće je postojanje najrazličitijih oblika veza, počev od onih koje se matematički mogu iskazati jednostavnom formulom, pa do onih veoma kompleksnih. Najjednostavniji oblik veze između pojava je linearna veza i u ovoj knjizi zadržaćemo se samo na takvim vezama Razlika između regresione i korelacione analize Prilikom istraživanja međuzavisnosti varijacija dve ili više pojava u statistici se primenjuju metode regresione i korelacione analize. Iako su ovi statističke metode u bliskoj vezi i međusobno se dopunjuju, između njih postoje i značajne razlike. Kod korelacije, pri analizi dve pojave svejedno je koja se od njih označava kao nezavisna, a koja kao zavisna promenljiva - dobija se identičan rezultat. Međutim, kao što ćemo videti u sledećoj glavi, pri ispitivanju korelacione veze između tri ili više pojava prethodno jedna od njih se mora definisati kao zavisna promenljiva, dok ostale dobijaju ulogu nezavisnih promenljivih. Cilj korelacione analize je da se ispita da li između varijacija posmatranih pojava postoji kvantitativno slaganje i, ako postoji, u kom stepenu. Kod regresione analize nužno je unapred identifikovati koja pojava će imati ulogu zavisne promenljive, a koja nezavisne promenljive. U statistici se kod regresije najčešće ne koristi termin "nezavisna promenljiva" 3, već objašnjavajuća promenljiva ili regresor. Naziva se objašnjavajuća jer pomoću nje pokušavamo da objasnimo varijacije zavisne promenljive. Koja promenljiva će biti izabrana za objašnjavajuću utvrđuje se na osnovu prethodnih teorijskih ili empirijskih saznanja, ili pretpostavki o prirodi analiziranih pojava. 3 Kod regresije se izbegava izraz nezavisna promenljiva jer to implicira da je X uzrok, a Y posledica. Međutim, regresionom analizom je nemoguće dokazati uzročnu vezu između pojava. Svrha regresije jeste da se utvrdi oblik veze, odnosno zavisnosti između posmatranih pojava. To se postiže pomoću odgovarajućeg regresionog modela. Regresioni model je takav stohastički model koji kroz matematičku formulu i niz odgovarajućih pretpostavki najbolje opisuje kvantitativnu zavisnost između varijacija posmatranih pojava u realnosti. Regresioni 49
51 model nije sam po sebi cilj regresije, već sredstvo koje nam služi da ocenimo i predvidimo vrednosti zavisne promenljive za željene vrednosti objašnjavajuće promenljive. Cilj regresione analize je da se odredi onaj regresioni model koji najbolje opisuje vezu između pojava i da se na osnovu toga modela ocene i predvide vrednosti zavisne promenljive Y za odabrane vrednosti objašnjavajuće promenljive X. Na osnovu navedenog jasno je da regresiona analiza ima daleko veći značaj u praktičnim istraživanjima od korelacije. Važno je napomenuti da pomoću regresije i korelacije nismo u stanju da otkrijemo da li između pojava postoji uzročno-posledična veza, u smislu da je jedna pojava uzrok, a druga posledica. To se može utvrditi drugim metodima kvantitativne ili pomoću kvalitativne analize. Prilikom istraživanja međusobnih veza dve promenljive primenjuju se metodi proste (eng. simple) regresione i korelacione analize, a u slučaju posmatranja više promenljivih, metodi višestruke (eng. multiple) regresije i korelacije. Reč "prosta" znači samo to da su u pitanju dve pojave, a nikako da je analiza jednostavna. U ovoj knjizi zadržaćemo se samo na prostoj korelaciji i regresiji Dijagram raspršenosti Dijagram raspršenosti (engl. scatter diagram) je dijagram kojim se prikazuje veza između dve kvantitativne promenljive. Bitno je shvatiti da se vrednosti ovih promenljivih dobijaju na osnovu merenja na istim jedinicama posmatranja (na primer istim studentima, istim firmama itd.). Na osnovu merenja dolazi se do uređenih parova podataka (x 1,y 1 ), (x 2, y 2 ),... itd. Pretpostavimo da nas interesuje da li između visine i težine studenata Vašeg univerziteta postoji kvantitativno slaganje. Kod svakog studenta morali bismo da izmerimo visinu i težinu i na taj način formirali bismo uređenu listu parova podataka. Svaki od tih parova sastojao bi se od dva broja jednog koji bi označavao težinu određenog studenta i drugi koji bi se odnosio na njegovu visinu, na primer, (75 kg ; 185 cm). Osnovni skup u ovom slučaju čine svi parovi vrednosti (x i, y i ), pa kažemo da on sadrži sve realizovane vrednosti dvodimenzionalne promenljive. Dijagram raspršenosti nema smisla koristiti ako nemamo uređene parove podataka, na primer nema smisla grafički prikazivati podatke za visinu 10 studenata u Kragujevcu i težinu 10 studenata u Subotici. Ovo ujedno važi i za regresionu i korelacionu analizu. Dijagram raspršenosti se konstruiše u pravouglom koordinatnom sistemu. Pri tome se na apscisnu osu nanose jedinice pojave koju smo označili nezavisnom (u regresionoj analizi objašnjavajućom) promenljivom X, a na ordinatnu osu jedinice zavisne promenljive Y. Ucrtavanjem svih empirijskih parova podataka može se dobiti važna slika o eventualnom postojanju, obliku, smeru i jačini veze između posmatranih pojava. Primer 11.1: Uzmimo podatke Tabele 11.1, koja pokazuje izdatke za propagandu (u milionima dinara) i prihod od prodaje (u 100 miliona dinara), deset, na slučaj odabranih računarskih firmi u Srbiji. Tabela 11.1 Izdaci za propagandu i prihod od prodaje 10 računarskih firmi, na osnovu slučajnog uzorka Koju promenljivu označiti kao X, a koju kao Y? Odgovor zavisi od toga da li sprovodimo korelacionu ili regresionu analizu. Ako istražujemo vezu između posmatrane dve pojave, 50
52 potpuno je svejedno da li ćemo na X osu nanositi vrednosti prve ili druge promenljive. Međutim, ako želimo da ispitamo da li se na osnovu ulaganja u propagandu mogu objasniti varijacije prodaje, kao objašnjavajuću promenljivu odabraćemo izdatke za propagandu. Budući da ćemo podatke Tabele 11.1 koristiti i u regresionoj analizi, izdatke za propagandu ćemo označiti kao X, a prodaju kao Y. Podatke uzorka prikazaćemo grafički pomoću dijagrama raspršenosti na Slici Slika 11.1 Dijagram raspršenosti za podatke из Tabele 11.1 Dijagram raspršenosti na Slici 11.1 pokazuje da između varijacija posmatranih pojava postoji kvantitativno slaganje. Naime, sa porastom ulaganja u propagandu raste i prihod od prodaje. Dakle, vidimo da se radi o direktnoj vezi između pojava. Takođe, raspored tačaka se približno grupiše u vidu prave linije, što nam govori da je u pitanju linearna veza. Međutim, sve tačke se ne nalaze na samoj pravoj liniji, jer bi se onda radilo o funkcionalnom slaganju, što je izuzetno redak slučaj u ekonomiji. U pitanju je, dakle, stohastička veza, kod koje individualni slučajevi pokazuju odstupanja od opšte pravilnosti. Ukoliko su tačke više raspršene u odnosu na pravu liniju, utoliko je i slabija međuzavisnost dve pojave, i obrnuto. U slučaju kada je raspored tačaka sasvim raspršen zaključuje se da ne postoji nikakvo kvantitativno slaganje varijacija dve pojave. Na Slici 11.2 prikazane su različite mogućnosti povezanosti varijacija dve pojave na odgovarajućim dijagramima raspršenosti. Od navedenih grafičkih prikaza obratimo pažnju na onaj pod i) zbog njegove posebne važnosti u daljem izlaganju. Iako na prvi pogled izgleda da postoji pravolinijska funkcionalna veza između pojava, to nije tačno, jer za bilo koje vrednosti promenljive X promenljiva Y ostaje konstantna. Takođe, upozorimo na jednu specifičnost dijagrama raspršenosti na Slici 11.1 u odnosu na dijagrame sa Slike Naime, ranije smo naveli da kod stohastičke veze za svaku vrednost X postoji čitav niz vrednosti Y, a to se ne može uočiti na Slici 11.1 (izuzev što za vrednosti X = 3 i X = 5 imamo po dve vrednosti Y). Razlog je u tome što u našem primeru raspolažemo sa relativno malim uzorkom od samo 10 firmi. 51
53 Slika Primeri različitih oblika veza na dijagramima raspršenosti Na osnovu svega navedenog možemo zaključiti da dijagramom raspršenosti grafički prikazujemo varijacije dve pojave u cilju sagledavanja: 1) da li između njih postoji kvantitativno slaganje, 2) ako slaganje postoji, koji je njegov oblik (linearni ili krivolinijski), 3) koji je smer slaganja (direktni ili inverzni), i 4) koja je jačina slaganja. Bez dijagrama raspršenosti često se u praksi mogu dobiti potpuno nevalidni zaključci; stoga preporučujemo da se obavezno, pre bilo kakve kvantitativne analize, podaci prikažu na ovom dijagramu. 52
54 6. TEORIJA VEROVATNOĆE Teorija verovatnoće proučava zakonitosti koje važe za slučajne pojave i slučajne eksperimente, tj. pojave čiji se tok ne može sa sigurnošću predvideti, odnosno eksperimente čiji se rezultati ne mogu sa sigurnošcu predvideti. Razlika između pojave i eksperimenta je ta što pojavu samo pratimo dok eksperiment izvodimo. Primeri slučajnih pojava su: kretanje temperature vazduha u nekom mestu tokom vremena, pojava neispravnih proizvoda u procesu proizvodnje, promena sastava prirodnih sirovina itd. Primeri slučajnih eksperimenata su: bacanje kocke ili novčića, eksperimenti koje izvodimo u laboratorijama radi proučavanja nekih slučajnih pojava u hemijsko-tehnološkim procesima. Pod slučajnim eksperimentom ili opitom u teoriji verovatnoće podrazumeva se eksperiment koji se može neograničen broj puta obaviti pod istim uslovima, ali čiji ishod se ne može sa sigurnošću predvideti. Rezultate (ishode) takvog eksperimenta zvaćemo slučajnim događajima. Uzmimo popularan primer slučajnog eksperimenta: bacanje kocke sa brojevima 1 6. Neki slučajni događaji koji mogu nastupiti u tom slučajnom eksperimentu su recimo: dobijanje parnog broja, pojavljivanje broja manjeg od 5, dobijanje šestice. Prva dva događaja u datom primeru se mogu ostvariti na više načina. Tako se prvi realizuje ako je rezultat bacanja 2, 4 ili 6, dok se drugi realizuje ako je rezultat 1, 2, 3 ili 4. Dakle, prvom događaju odgovara skup {2, 4, 6}, dok drugom možemo da dodelimo skup {1, 2, 3, 4}. Za razliku od prva dva događaja, treći se može ostvariti samo na jedan način i zato ga zovemo elementaran događaj i odgovara mu jednočlani skup {6}. Prva dva događaja možemo zvati složenim. Složenom događaju odgovaraju višečlani skupovi 2 čiji su elementi pojedini elementarni događaji, čije nastupanje povlači ili uključuje ostvarivanje datog složenog događaja. Uopšte, ako neki događaj (elementaran ili složen) povlači realizaciju nekog drugog događaja, znači da je skup elementarnih ishoda, koji odgovara prvom događaju, podskup skupa elementarnih ishoda za drugi događaj. Na primer, događaj da se bacanjem kocke dobije 1 ili 3, kome odgovara skup {1, 3}, povlači ostvarivanje događaja da se bacanjem kocke dobija neparan rezultat, kome odgovara skup {1, 3, 5}. Veza između skupova je: {1, 3} {1, 3, 5} Klasična definicija verovatnoće Skup svih mogućih elementarnih događaja za neki eksperiment zvaćemo prostor elementarnih događaja. Klasična definicija verovatnoće je primenljiva na slučajne eksperimente kod kojih je prostor elementarnih događaja konačan, tj. sadrži n elementarnih događaja i pri tome svaki od njih ima jednaku mogućnost da nastupi. Tipični primeri su bacanje kocke ili novčića bez ikakvih trikova sa ciljem dobijanja željenog rezultata. 53
55 Zamislimo dakle neki eksperiment kod koga je podjednako moguće nastupanje bilo kog od ukupno n elementarnih događaja. Verovatnoća nastupanja nekog događaja A jednaka je količniku broja povoljnih ishoda m, tj. broja elementarnih događaja koji povlače ostvarenje događaja A, i broja svih mogućih ishoda n. Primer 1a. Kolika je verovatnoća dobijanja parnog broja pri bacanju kocke? Rešenje: Elementarni događaji koji povlače nastupanje posmatranog složenog događaja A su dobijanje 2, 4 ili 6 ima ih 3, m = 3.Ukupan broj svih elementarnih događaja ovde je 6, n = 6. Prema formuli: Primer 1b. Slučajni eksperiment se sastoji u izvlačenju jedne od kuglica iz kese koja sadrži 64 kuglice, od toga: 8 crvenih 15 belih 24 crne 17 narandžastih Kolika je verovatnoća događaja A - izvlačenje crvene kuglice? Rešenje: Broj povoljnih događaja, izvlačenja bilo koje crvene kuglice, jednak je broju crvenih kuglica m = 8. Ukupan broj mogućih ishoda je 64: Vidimo da događajima koji se češće javljaju kao ishod eksperimenta pripada i veća verovatnoća. Tako, verovatnoću nekog događaja možemo da posmatramo kao meru mogućnosti da taj događaj nastupi. Iz samog značenja bojeva m i n sledi da je m _ n, što kao posledicu ima: 0 P(A) 1 Ako je neki događaj nemoguć, odgovara mu prazan skup elementarnih događaja tj. imamo m = 0 i njegova verovatnoća mogućnost da nastupi, jednaka je nuli: P(Ф) = 0, gde smo sa Ф označili nemoguć događaj. Naprotiv, ako svaki od n mogućih ishoda povlači ostvarenje nekog događaja, kažemo da je on siguran događaj, E i pošto je m = n, njegova verovatnoća je jednaka jedinici: P(E) = 1. Da bi se računala verovatnoća po klasičnoj definiciji (1.1), u složenijim slučajevima, neophodno je poznavanje kombinatorike Statistička definicija verovatnoće Kod mnogih slučajnih pojava ili eksperimenata nije moguće unapred apriori, pomoću klasične definicije (1.1) odrediti verovatnoću nekog događaja. Na primer, u nekom tehnološkom procesu ne može se teorijski, tj. unapred odrediti verovatnoća pojave škarta. Posmatrajmo sada poznati eksperiment bacanja kocke. Formula (1.1) za verovatnoću događaja A da se pri bacanju kocke pojavi, recimo, broj 6 daje: 54
56 To znači, da ako bacamo kocku n puta, možemo da očekujemo da ćemo šesticu dobiti približno m = n/6 puta. Na primer, u n = 600 bacanja očekujemo da čemo šesticu dobiti oko 100 puta. Broj ostvarivanja nekog događaja m u n ponovljenih eksperimenata zvaćemo (apsolutna) učestalost ili frekvenca događaja. U posmatranom primeru, u n ponovljenih eksperimenata, očekivana frekvenca dobijanja šestice jednaka je n/6. Isto tako, ako zamislimo da smo nekako došli do verovatnoće pojave neispravnog proizvoda p, u nekoj serijskoj proizvodnji, recimo p = 0.1, tada u uzorku od 100 komada možemo očekivati 10 neispravnih, ali stvarno taj broj može biti 8, 9, 10, 12 itd., dakle neki broj oko broja 10. Dakle, očekivana učestalost pojave škarta u uzorku od 100 komada je m = 10. Količnik učestalosti m i broja ponavljanja eksperimenta, n naziva se relativna učestalost (frekvenca) događaja A: Možemo očekivati da ce relativna učestalost dobijanja šestice pri bacanju kocke biti približno 1/6, odnosno _(A) _ P(A). Naravno, u nekih n bacanja kocke _ će imati jednu vrednost, a u n narednih bacanja neku drugu vrednost. Ono što iskustvo pokazuje je da ako je n dovoljno veliko, relativne učestalosti nekog događaja u različitim serijama od po n izvođenja eksperimenata malo se razlikuju među sobom. Šta više, kada n raste, frekvence ostvarene u pojedinim serijama se sve manje među sobom razlikuju. Tako, ako bi kocku bacali 600, 6000, i puta, mogli bi dobiti sledeće učestalosti pojavljivanja šestice: odnosno relativne učestalosti: 105, 983, 10150, , 0.164, 0.170, Primećujemo da se relativna učestalost približava teorijskoj verovatnoći posmatranog događaja (1/6 _0.168) kada se n uvećava. Svojstvo relativnih frekvenci slučajnog događaja da se grupišu oko nekog broja kada se broj ponavljanja slučajnih eksperimenata neograničeno povećava, u skladu je sa tzv. zakonom velikih brojeva, i omogućuje da se verovatnoća slučajnog događaja definiše preko relativnih frekvenci, budući da je broj oko koga se relativne frekvence grupišu upravo jednak verovatnoći: (n veliko) Daćemo, bez dokaza, Bernulijev (Bernulli) zakon velikih brojeva, na kome se zasniva formula (1.7) za određivanje verovatnoće događaja nakon realizacije eksperimenata (aposteriori). Kada n,relativna učestalost događaja A, (A) = m/ n teži po verovatnoći stvarnoj verovatnoći događaja: za proizvoljno mali broj. U kraćoj notaciji: =1 55
57 Znači da ce za dovoljno veliko n, relativna učestalost (gotovo) sigurno biti, dobra aproksimacija stvarne verovatnoće događaja P(A). Primer 1.10 U dužem vremenskom intervalu utvrđeno je da mašina za automatsko pakovanje hrane daje 2% paketa ispod propisane težine. Kontrolor je uzeo slučajan uzorak od 50 paketa. Odrediti očekivani broj neispravnih paketa. Rešenje: Podatak 0.02 (2%) predstavlja relativnu frekvencu pojave defektnog paketa (A) I u skladu sa (1.7) usvojićemo ga kao procenu verovatnoće pojave defektnog paketa: Očekivani broj defektnih paketa u n = 50 komada biće jednak apsolutnoj frekvenci: 56
58 7. RAČUNARSKO MODELOVANJE I SIMULACIJA PROCESA Računarski modeli predstavljaju prikaz matematičkih modela u obliku računarskih programa korišćenjem programskih jezika i usko su vezani za razvoj računarske nauke. Računarsko modelovanje i simulacija procesa imaju značajnu ulogu u nastavi prirodnih i tehničkih predmeta, jer pomažu studentima da lakše shvate bitne karakteristike nekog realnog sistema ili princip rada mašina i uređaja. Znanja studenata se produbljuju i proširuju korišćenjem računarskog modelovanja i simulacije procesa, kao što su animacije, apleti i sopstveni simulacioni programi urađeni u pogodnim programima, kao što su: Matlab, Electronics Workbench, Power World Simulator itd. Prilikom izrade (formiranja) računarskog modela treba se pridržavati sledećih preporuka: granice modela treba odabrati tako da on obuhvata samo pojave od interesa, model ne sme biti suviše složen ni detaljan, model ne sme biti suviše pojednostavljen, model se može rastaviti na više modula radi lakše izrade i provere, za razvoj algoritama i programa treba koristiti neku od proverenih metoda, treba proveriti logičku i kvantitativnu ispravnost i modela i modula. Analiza i projektovanje realnih sistema ne mogu se zamisliti bez simulacije ponašanja tih realnih sistema na računaru. Simulacijom ponašanja realnog sistema na računaru mogu se istraživati ne samo prelazne pojave nego i uticaji pojedinih parametara elemenata na te pojave. Na taj način moguće je odabrati element s takvim karakteristikama koje, zajedno s karakteristikama ostalih elemenata realnog sistema, daju optimalno ponašanje čitavog realnog sistema. Povezivanjem modela sa realnim sistemom omogućeno je istraživanje i podešavanje tih sistema u uslovima rada, koji su veoma bliski realnim. Takođe, mogu se simulirati i istraživati ponašanja realnih sistema u raznim normalnim i nenormalnim režimima koja mogu nastati u pogonu. Takav način eksperimentisanja je u pravilu jednostavniji, brži i jeftiniji nego eksperimentisanje na realnom sistemu. Metoda simulacije omogućava uz upotrebu savremenih računara, teorijsko simuliranje (oponašanje) realnih sistema (stvarnih pojava i procesa) kako bi se između velikog broja mogućih rešenja pronašlo ono najpovoljnije. Problem simulacije je u verodostojnosti geneze simulacijskog fenomena. Simulacijom se uspostavlja veza između modela i računara. Verifikacijom programa se provera da li program verno prenosi model na računar i na tačnost kojom računar vrši instrukcije. Simulacije ponašanja realnih sistema na računaru omogućavaju "eksperimentisanje" na računaru umesto na realnom sistemu što je posebno važno u fazi projektovanja realnih sistema. Simulacija predstavlja izvršenje modela i formiranje određenih rezultata. Prednosti simulacija su u tome što je to ekonomičniji način dobijanja odgovora na postavljeno pitanje u odnosu na sprovođenje eksperimenata. Eksperimenti predstavljaju skup ali dragocen izvor informacija i rezultata, naročito kada se rade u realnim uslovima. Na osnovu rezultata simulacija mogu se formirati analize tipa Šta ako. Samo svojstvo simulacija da omogućavaju menjanje ulaznih i izlaznih podataka modela, omogućava boljem razumevanju kako funkcioniše modela, a time i realni sistem koga model predstavlja (zamenjuje). 57
59 Modelovanje i simulacije predstavljaju složenu aktivnost koja sadrži tri elementa: 1) Realni sistem, je uređen skup elemenata koji formiraju jednu celinu i deluju zajednički kako bi ostvarili zadati cilj. Realni sistem predstavlja izvor podataka za izradu modela. 2) Model, je na pojednostavljen (apstraktan) način prikazan neki realni sistem, koji prikazuje strukturu, komponente i njihovo uzajamno delovanje u realnom sistemu. Računarski model predstavlja program koji opisuje ponašanje simuliranog realnog sistema. Model ima svoje elemente koji su opisani atributima i promenljivima. 3) Računar, je uređaj na kome se izvršava program modela i koji daje određene rezultate tokom vremena na osnovu ulaznih podataka. Računarsko modelovanje i simulacija procesa se koristi kod: pravljenje prototipova, predstavljanje određenih procesa u edukativne svrhe, predstavljanje novih uslova i sredina, distribucija vode, struje, gasa, službi za hitne intervencije, računarskih sistema, saobraćajnih sistema (raskrsnica, luka itd.), proizvodnih pogona, banki, pošta, samoposluga itd Primena softverskog paketa MATLAB u računarskom modelovanju i simulaciji procesa Programski paket MATLAB je namenjen za rešavanje različitih problema iz linearne i vektorske algebre korišćenjem prevashodno numeričkih metoda. Matrični proračuni predstavljaju osnovu MATLAB-a, jednostavno i brzo se izvode, te je na ovom polju MATLAB vodeći svetski programski paket. Operacije sa matricama su od posebnog značaja, jer se realni sistemi sa više ulaza, promenjivih i izlaza zadaju pomoći matrica. MATLAB se može koristiti za rešavanje i drugih tipova matematičkih problema kao što su određeni integrali, nelinearne jednačine, diferencijalne jednačine i dr. Ove probleme MATLAB 58
60 rešava pomoću optimizovanih numeričkih metoda koje su inkorporirane u programski paket i pokreću se pomoću određenih naredbi. Na taj način MATLAB omogućava jednostavno rešavanje inženjerskih problema i dobijene rezultate prikazuje na jasan i pregledan način, pomoću grafika i tabela (matrica rezultata). U MATLAB-u se mogu rešavati različiti problemi pomoću posebnih dodatnih modula za: regulaciju procesa (Control System Toolbox), formiranje procesnih šema, odnosno blok dijagrama (Simulink), robustno upravljanje (Robust Control Toolbox). Osim ovih modula u MATLABu postoji niz drugih, koji služe za rešavanje različitih inženjerskih problema: parcijalnih diferencijalnih jednačina (Partial Differential Equation Toolbox), optimizaciju (Optimization Toolbox), formiranje neuronskih mreža (Neural Network Toolbox), obradu podataka: o digitalnu obradu signala (Signal Processing Toolbox), o akviziciju podataka (Data Acquisition Toolbox), o statističku obradu podataka (Statistics Toolbox), o baze podataka (Database Toolbox) itd. MATLAB sadrži biblioteku rutina (MAPLE) za simboličko rešavanje problema. Na taj način se mogu dobiti analitička rešenja sistema linearnih jednačina, diferencijalnih jednačina, određenih i neodređenih integrala. Iz oblasti automatskog upravljanja značajno je određivanje Laplasove i Furijeove transformacije različitih funkcija. 1. Pokretanje programa Korišćenjem miša u Windows Desktop-u treba izabrati Start/Programs/Matlab/Matlab. Na taj način otvara se osnovni prozor MATLAB-a koji se po default-u sasatoji od: komandnog prozora, prozora istorije komandi i prozora tekućih direktorijuma. Kao i ostali Windows programi MATLAB pri vrhu prozora sadrži spisak svih menija (File, Edit, View,...) i bar za standardno formiranje. Pregledati menije i promeniti raspored osnovnog prozora pomoću View/Desktop Layout/Simple koji se sastoji samo od komandnog prozora i prozora istorije komandi. 2. Osnovne operacije MATLAB koristi komandni jezik jednostavne sintakse. Komande u MATLAB-u se upisuju u poslednju, aktivnu, liniju komandnog prozora koja počinje sa oznakom >>. Operacije se upisuju u komandnu liniju i izvršavaju pomoću tastera Enter. 3. Korišćenje pomoći (Help-a) Informacije o pojedinim naredbama se mogu dobiti primenom naredbe Help. Na primer: >> help laplace prikazuje opis naredbe laplace. Detaljnije informacije o pojedinim mogućnostima programa mogu se naći i korišćenjem opcija iz menija Help u osnovnom MATLAB prozoru. 59
61 8. EKOLOŠKO MODELOVANJE Zaštita životne sredine svakim danom postaje sve aktuelnija tema kojom se bavi sve veći broj ljudi. Klimatske promene, kisele kiše, ekološki akcidenti, gubitak biodiverziteta i problem otpada samo su neki od ekoloških problema kojim se bavi ekologija (nauka o zaštiti životne sredine). Svi ovi problemi su veoma različiti po pitanju vremenskog i prostornog opsega. Vremenski opseg može biti veoma dugačak, kao kod klimatskih promena, ili sasvim kratak, što je slučaj kod nekih ekoloških akcidenata. Prostorni opseg može biti ograničen na užu lokalnu oblast, na primer kod poplava, ili može imati širi pa čak i globalni karakter, što je slučaj sa podizanjem nivoa mora i okeana. Pored toga važno je naglasiti da ovi ekološki problemi mogu imati jedan uzrok ili što je mnogo češće slučaj mogu biti uzrokovani delovanjem više međusobno povezanih faktora u životnoj sredini. Istraživanja ekoloških problema mogu biti skupa, teška a ponekad i nemoguća zbog toga se ova ispativanja često vrše metodom ekološkog modelovanja, odnosno istraživanja se vrše na ekološkim modelima a zatim se dobijeni rezultati istraživanja sa ekoloških modela prenose na realne (ekološke) sisteme. Ekološko modelovanje ima velike mogućnosti tako da se koristi u različitim oblatima ekologije, kao što su: Klimatologija, koja se bavi proučavanjem klimatskih promena. Okeanografija, koja se bavi proučavanjem uticaja promena temperature morskih struja na veremenske prilike. Procena rizika od hazardnih situacija, koja se bavi proučavanjem verovatnoće nastanka poplava i predviđanja mogućih negativvnih posledica koje mogu uzrokovati (ugrožavanja bezbednosti ljudi i životne sredine, oštećenja objekata itd.). Populaciona biologija, koja se bavi proučavanjem stanja i brojnosti populacije određene vrste i promena tih parametara usled različitih antropogenih aktivnosti. Ekologija, koja se bavi modelovanjme stanja biotičkih i abiotičkih faktora i njihovim promenama uzrokovanim antropogenim uticajima. Procena uticaja na životnu sredinu proizvoda koji tek treba da se proizvedu. Ekološka epidemiologija, proučavanje uticaja vazdušnog zagađenja na pojavu respiratornih oboljenja kao što je astma. Ekološko zakonodavstvo, uz pomoć modela se mogu odrediti metodologije uzimanja uzoraka kako bi se ispoštovali svi relevatni zakoni i vršio adekvatan monitoring životne sredine Faze (koraci) izrade ekološkog modela Pravilan postupak izrade modela obezbeđuje da model bude validna predstava realnog sistema koji se istražuje, da ga je moguće lako istraživati (i to uglavnom uz pomoć računara), da se izradi unutar troškovnih i vremenskih ograničenja i da se može efikasno primenjivati. Da bi ekološki model mogao da verodostojno (uspešno) simulira (oponaša, predstavlja) neki realni sistem potrebno je pridržavati se određene metodologije prilikom njegove izrade. 60
62 Nakon što se izvrši primena ekološkog modela važno je da se na neki način sam model verifikuje. Ekološki mideli se mogu izrađivati na različite načune, a u nastavku je prikazan jedan od mogućih postupaka. Izrada (formiranje, razvoj) ekološkog modela, kao i svakog drugog modela realnog sistema, se izvodi kroz više faza (koraka), slika 1: 1. Definisanje (identifikacija) problema koga korisnik modela želi da reši korišćenjem tog modela. 2. Upoznavanje realnog sistema koji se istražuje (proučava). 3. Izrada konceptualnog modela. 4. Postavljanje (usvajanje) pretpostavki modela. 5. Izrada (formiranje, razvoj) matematičkog modela, tj. formiranje jednačina koje na adekvatan način opisuju ponašanje realnog sistema. 6. Izrada računarskog modela: o izbor odgovarajuće nameričke metode i programskog jezika u kome će se rešavati matematički model i o formiranje algoritma za rešavanje matematičkog modela i izrada programa (programiranje). 7. Verifikacija računarskog modela (testiranje programa) - provera da li računarski model verno predstavlja matematički model i 8. Validacija (vrednovanje) modela realnog sistema provera da li model verno predstavlja realni sistem. 9. Praktična primena (implementacija) modela. 61
63 Definisanje (identifikacija) problema Upoznavanje realnog sistema Izrada koncepualnog modela Postavljanje (usvajanje) pretpostavki Izrada matematičkog modela Izrada računarskog modela Da li računarski model verno predstavlja matematički model Ne Da Da li model verno predstavlja realni sistem Ne Da Praktična primena modela Slika 1. Faze izrade (formiranja) ekološkog modela 62
64 U praksi, granice između ovih faza nisu uvek precizno definisane i prelaz iz jedne u drugu fazu je retko kad oštar kao što je na šemi prikazano. Bez obzira na to ova šema predstavlja koristan okvir za razumevanje osnovnih principa izrade modela. Prvo treba ostvariti prelaz sa realnog sistema na konceptualni model, zatim sa konceptualnog na matematički model i sa matematičkog na računarski model. Potom simulacijama na računaru treba izvršiti proveru ispravnosti rada programa i modela. Izrada modela je najčešće proces koji zahteva ponavljanje i isprobavanje različitih rešenja i ispravljanje uočenih grešaka. Model se obično pravi kroz više faza (koraka) koji povećavaju njegovu kompleksnost sve dok ne bude u stanju da uspešno oponaša realni (stvarni) sistem koji se istražuje (proučava). Kada se takav model uradi onda se koristi za simulaciju ponašanja realnog sistema. Za realizaciju svake od navedenih faza potrebna su različita znanja i veštine. Malo je osoba koje imaju sposobnost da uspešno realizuju sve navedene faza razvoja modela. Zbog toga izrada modela zahteva formiranje tima, pri čemu je važno ostvariti koordinaciju i komunikaciju između članova tima. Modeli izrađeni od strane različitih autora ili različitih timova uvek se razlikuju, tako da će n različitih osoba ili timova formirati n različitih modela Definisanje (identifikacija) problema koga korisnik modela želi da reši korišćenjem tog modela Prva faza izrade modela jeste definisanje (identifikacija) problema koga korisnik modela želi da reši korišćenjem tog modela. Problem treba da bude jasno i precizno definisan, kako bi korisnik modela korišćenjem tog modela mogao doći do rešenja problema. Ako se problem ne definiše jasno i precizno proces izrade modela može biti težak, složen i oduzeti puno vremena i što je najgore može se desiti da model ne predstavlja verodostojnu zamenu za realni sistem (predmet modelovanja). Prilikom definisanja problema treba obratiti pažnju na opseg samog modela. Treba razgraničiti elemente naučnog pitanja kojima model treba da se bavi i one kojima ne treba da se bavi. Opseg modela treba ograničiti na različite načine kako bi se dobilo pogodno rešenje. Na primer, nekad će treba izraditi model tako da on predstavlja deo ekološkog sistema, određenu prostornu oblast ili određeni vremenski period. Pri tome postavljeni ciljevi ne treba da budu suviše uski, ali ni suviše široki. Izrada modela treba da bude u skladu sa zadatim vremenskim, troškovnim i kadrovskim ograničenjima Upoznavanje realnog sistema koji se istražuje (proučava) Upoznavanje (posmatranje, opažanje) realnog sistema (predmeta modelovanja) koji se istražuje (proučava) se vrši sa ciljem da se identifikuju njegove ključne komponente, zatim njegovi ulazni i izlazni parametri, odnosi između njih, procesi i struktura koji upravljaju njihovim interakcijama. 63
65 Izrada konceptualnog modela Sledeća faza (korak) je izrada (formiranje, razvoj) konceptualnog modela koji treba da na verodostojan način opiše realni sistem. Konceptualni model se uglavnom pravi u obliku dijagrama. Ova faza je od fundamentalnog značaja za uspeh modelovanja. Ovom fazom se obezbeđuju svi potrebni podaci za fazu izradu matematičkog modela, kao i smernice za budući rad. Prvi zadatak ove faze je odluka da li je potrebno dati realni sistem podeliti na određeni broj manjih podsistema, koji se dalje mogu rešavati ili jedan po jedan ili paralelno Zatim treba postaviti primarne veze između elementa i promenjivih putem pažljive analize i detaljne observacije. Jedan od načina da se ovo postigne je i praćenje sledećih koraka: definisanje granica realnog sistema koji se modeluje, odabir ključnih komponenti, na primer promenljivih, procena brojčanih vrednosti promenljivih, verbalno, statističko ili analitičko definisanje veza između promenljivih. Najčešće je suština izrade konceptualnog modela izrada dijagrama koji predstavlja ključne elemente proučavanog realnog sistema (fenomena, procesa), kao i sve bitne odnose između tih elemenata. Ovi dijagrami, u zavisnosti od posmatranog problema, mogu biti prosti ili veoma složeni. Konceptualni dijagrami su ustvari skupovi odgovarajućih simbola koji su prikazani na odgovarajući način. Postoji veliki broj već postojećih simbola koji imaju poznato značenje koji se mogu koristiti u tu svrhu. Osim toga moguće je i formiranje novih, sopstvenih simbola. Odabir simbola koji će se koristiti zavisi i od problematike i zadatka koji model treba da ispuni. Za problematiku modelovanja ekoloških sistema često se koriste simboli iz Forrester-ovih dijagrama. Na Slici 2 dat je prikaz nekih od simbola iz Forrester-ovih dijagrama. 64
66 Slika 2. Neki od simbola iz Forrester-ovih dijagrama Treba naglasiti u određenim programskim paketima za modelovanje, kao što je na primer VENSIM, već postoje odgovarajući simboli i metodologija koja se koriste za izradu dijagrama. Svaki simbol čini jedan element ekološkog modela. U elemente nekog ekološkog modela spadaju različiti entiteti, a neki od najzastupljenijih su prikazani u tabeli 1. Tabela 1. Ključni elementi ekološkog sistema 65
67 1. Izrada referentnog grafika 2. Izrada dijagrama sa rezervama i protocima (stock and flow diagram) 66
68 3. Izrada dijagrama uzročne petlje (causal loop diagram) 67
69 Postavljanje (usvajanje) pretpostavki modela Svaki model se zasnova na pretpostavkama. Pretpostavke mogu biti postavljene u cilju pojednostavljivanja kompleksnih ekoloških modela (tj. postavljanja što manjeg broja jednačina), što je često potrebno da bi se mogao izraditi funkcionalan model, ili zbog ograničenosti naših znanja o posmatranom ekološkom sistemu. Za neke od pretpostavki koje se postave na početku izrade modela se kasnije može ispostaviti da su netačne, i tada je često neophodno izvršiti određene korekcije na samom modelu. Sa druge strane, za neke pretpostavke se od početka zna da su netačne, ali se bez obzira na to one zadržavaju, jer su neophodne radi jednostavnosti i efikasnosti samog modela, a nemaju značajan uticaj na rezultat samog modela. Ono što je važno je da svaka pretpostavka koja se koristi u modelu treba da bude prepoznatljiva, razumljiva i jasna. Glavni razlog za ovo je da se razjasne priroda, svrha i ograničenja samog modela, a pored toga i da se potencijalnim korisnicima omogući razumevanje samog modela Izrada (formiranje) matematičkog modela, tj. formiranje jednačina koje na adekvatan način opisuju ponašanje realnog sistema Realni sistem definisan kao uređaj ili proces koji ima jedan ili više ulaza odnosno jedan ili više izlaza, može da se modeluje na više načina. Matematički model ima brojne prednosti u odnosu na ostale modele, između ostalog omogućava: jasno definisanje promenljivih, eksplicitno izražavanje pretpostavki, određivanje izlaznih promenljivih na osnovu kompleksnosti realacija modela. Generalno, linearne modele je lakše rešavati nego nelinearne, obične diferencijalne jednačine je lakše je rešavati nego parcijalne diferencijalne jednačine, analitičke funckije lakše je rešavati nego beskonačne nizove, Beselove funkcije i sl. Takođe, determinističke modele je lakše rešavati nego stohastički. Opšta metodologija izrade matematičkog modela se sastoji od četiri koraka: deifinisanja sistema, određivanja ulaznih veličina sistema, određivanja izlaznih veličina sistema, određivanja relacija između ulaznih veličina, izlaznih veličina i parametara sistema. U prvom koraku potrebno je jasno definisati šta je realni sistem, koji se istražuje (proučava), u kakvom su odnosu delovi sistema (ponekad povezanost delova sistema nije od izrazite važnosti za problem koji se rešava), koji se cilj želi postići itd. Postupak modelovanja zahteva jasno definisanje ulaznih i izlaznih veličina. Za obe grupe veličina važno je uočiti sledeće: identifikovati ih, po mogućnosti meriti ih, kroz iterativni postupak analize i modelovanja odrediti koje su veličine značajne i konačno, u kakvom su odnosu. Neke od ulaznih veličina mogu da budu kontrolabilne i poželjne, dok druge mogu da budu nekotrolabilne i nepoželjne. Vremenski uslovi, kao što su: temperatura, vlaga, brzina vetra,, predstavljaju nekontrolabilne ulazne veličine prilikom formiranja matematičkog modela. 68
70 Ozbiljne teškoće u postupku modelovanja nastaju kada spoljašnji nekontrolabilni faktori imaju veliki uticaj na analiziranu pojavu ili proces. Određivanje relacija između ulaznih veličina, izlaznih veličina i parametara sistema predstavlja najteži korak u formiranju modela. Suština dobrog modelovanja se sastoji u određivanju značajnih promenljivih i formiranju relacija koje opisuju kako su one međusobno povezane. Generalni principi dobrog matematičkog modelovanja su: modelovanje započeti onim što je poznato, složene modele razvijati modularno, koristiti iterativni postupak, modelovati samo potrebne elemente, formirati pretpostavke navesti ograničenja, formirati ekvivalente pogodne za inženjersku praksu. Modelovanje započeti onim što je poznato U modelovanju je potrebno koristiti fundamentalne zakone. Složene modele razvijati modularno Modularni pristup podrazumeva postepeno proširenje modela. Ovakav postupak omogućava prelazak sa jednostavnih konfiguracija ka složenim konfiguracijama uz najefikasnije eliminisanje nedostataka koje sa sobom donosi modelovanje složenih sistema. Koristiti iterativni postupak Iterativni postupak pretpostavlja ponovni pokušaj, poželjan nakon određene modifikacije modela. Strukturna blok šema prikazana na slici 1. jasno ukazuje na važne petlje u procesu modifikacije. Unutar svakog bloka postoji mogućnost za manje iterativne petlje. Simulacije pomoću računara sadrže sledeće faze: formiranje rezultata proračuna, upoređivanje ovih rezultata sa očekivanim rezultatima za poznat slučaj poboljšanje modela do postizanja zadovoljavajuće tačnosti. Izuzetno je redak slučaj da se iz prvog pokušaja dobiju rezultati koji su sasvim zadovoljavajući i koji kao takvi ne zahtevaju poboljšaanje. Čak i autori najuspešnijih programskoh alata navode da bi u slučaju ponovnog modelovanja nekog problema to trebalo raditi drugačije, na još bolji način. Modelovanje je učenje. Iterativni postupak za poboljšanje modela jeste suština procesa modelovanja. Modelovati samo potrebne elemente Formiranje matematičkih jednačina koje na verodostojan način opisuju ponašanje realnog siustema često je prava umetnost. Potpuno korektno modelovanje svih elemenata sistema često dovodi do problema, s obzirom na veliki broj dodatnih detalja vezanih za ulazne i izlazne promenljive, kao i predugo vreme simulacije. Prema tome za modelovanje je neophodno veliko 69
71 inženjersko znanje u cilju uključivanja potrebnih elemenata, i u isto vreme, eliminisanje nepotrebnih elemenata. Modelovanje samo potrebnih karakteristika od velikog je značaja iz dva razloga: Sledeći korak u procesu izrade (formiranja) modela je formiranje matematičkog modela, koje obuhvata prevođenje konceptualnog modela u matematiči jezik (tj. postavljanje jednačina modela). Često ova faza predstavlja najizazovniji deo celokupnog procesa izrade modela. Nekada, zbog neophodnosti primene komplikovanih matematičih metoda. Međutim, češće zbog toga što postoji više načina kojim se matematički može predstaviti proučavani realni sistem, a nije očigledno koji od tih načina je najbolje primeniti. Zbog toga je postavljanje odgovarajuće matematičke formulacije modela, često, proces koji se zasniva na sistemu pokušaja i grešaka. U ovoj fazi se izrađuje matematički model, pri čemu se definiše preslikavanje funkcija između bitnih karakteristika predmeta modelovanja i modela za koje je utvrđena sličnost ili analogija. Definišu se veze između promenjivih i parametara u matematičkim formulacijama, provera određenosti i konzistentnosti modela. Pogodno je funkcionalnu zavisnost promenljivih kategorisati kao: definicione, empirijske i normativne relacije. Definicione relacije predstavljaju, većinom, balanse koji proističu iz fizičke prirode problema ili recimo nekih konvencija koje su uvedene u problem. Empirijske relacije su bazirane na istorijskim podacima, eksperimentalnim rezultatima, široko prihvaćenom rezonu i slično. Nedostatak empirijskih relacija može biti nepogodnost korišćenja podataka i zaključaka iz prošlog ponašanja sistema za buduće ponašanje. Promene u budućnosti se mogu ticati kako promena parametara već postojećih relacija tako i promene strukture relacija. Isto tako, empirijske relacije mogu da predstavljaju niži nivo performansi starog sistema te prema tome mogu biti neadekvatne za opis novog sistema. Treći tip relacija su normativne relacije u tom smislu da one predstavljaju način kako treba povezati promenljive da bi se postigla optimalna vrednost zadatog kriterijuma. Postoji veliki broj matematičkih modela koji se mogu koristiti za proučavanje ekoloških sistema. Postoji više načina po kojima ovi modeli mogu da se podele, a neki od njih su: U kojoj meri se modeli zasnivaju na teoriji ili observacijama teorijski nasuprot empirijskim modelima U kojoj meri nasumični (slučajni) događaji i efekti imaju značajnu ulogu u proučavanom sistemu, a samim tim i u modelu deterministički nasuprot stohastičkim modelima U kojoj meri se raspolaže znanjem o proučavanom sistemu koji model treba da predstavlja model crne kutije ( Black box) nasuprot modelu bele kutije (White box). Da li se model bavi ekološkim procesima koji su statični ili dinamični u odnosu na prostor i vreme statični nasuprot dinamičnim modelima Da li se model bavi eklološkim procesima za koje se uzima da funkcionišu na kontinualan ili diskretan način kontinualni nasuprot diskretnim modelima 70
72 Kako su prostorno uređeni podaci modela modeli sa raspodeljenim parametrima nasuprot modelima sa grupisanim parametrima Izrada računarskog modela Ovde je potrebno odlučiti da li će na primer biti usvojen simulacioni ili optimizacioni pristup, da li će promenljive modela biti stohastičke ili determinističke, da li će model biti nelinearan ili linearan, da li je moguće primeniti neki od već postojećih postupaka rešavanja. Veoma često se prilikom izbora načina rešavanja matematičkog modela izbor se svodi na sledeće dve alternative: nalaženje optimalnog rešenja uprošćene verzije problema i nalaženje približnog rešenja tačne formulacije problema. Može se zaključiti da je u praktičnoj primeni druga alternativa mnogo pogodnija i to uglavnom što je nalaženje optimalnog rešenja u praktičnim problemima skoro nemoguć zadatak. Кompletna predstava važnih faktora problema čak i da rešenje nije optimalno je vredniji od optimalnog rešenja osiromašenog problema. Analitičko i numeričko rešavanje matematičkog modela (formiranog sistema jednačina) zahteva odgovarajuće znanje iz teorijske matematike i računarskih metoda. Nakon izbora numeričkog načina rešavanja sledi implementacija na računaru, što zahteva odgovarajuću veštinu programiranja. Prilikom formiranja programa potrebno je voditi računa o njegovoj verifikaciji sa odgovarajućim matematičkim modelom. Pri tome je potrebno tako koncipirati model da omogući dobijanje rezultata koji se slažu sa rezultatima dobijenim na realnim sistemima. Uloga računara eksplicitno je uključena u faze formiranja i verifikacije programa. Međutim, razvoj matematičkog modela implicitno uključuje ulogu računara. Osoba iskusna u modelovanju i programiranju automatski teži onim matematičkim modelima koji se na najlakši i najefikasniji način rešavaju pomoću računara. U ovoj fazi potrebno je izabrati način na koji će biti rešen matematički model: numerički ili analitički i oceniti da li ga je moguće realizovati na računaru. Ako se izabere numerički način rešavanja matematičkog modela potrebno je: izabrati odgovarajuće nameričke metode i programski jezik u kome će se rešavati matematički model i formirati algoritam za rešavanje matematičkog modela i izraditi program (programirati). Kada su postavljene matematičke jednačinei bitne za model potrebno je izvršiti konvretovanje tih jednačina i formula u neki software (program), koji može obaviti simulacije modela uz pomoć računara. Postoji ogroman broj programskih jezika koji se mogu koristiti za modelovanje na računaru. Izbor određenog programskog jezika zavisi od dostupnosti, cene, prethodnog iskustva, lakoće rukovanja, očekivanih rezultata, početnih ciljeva, dostupnih podataka, prilagođenosti podataka određenom programu i drugih parametara. Kada su u pitanju programska rešenja moguće je izvršiti podelu na sledeće kategorije: 1. Programi za rad sa tabelama (Spreadsheets), u koje spadaju na primer: Calc, Excel, Gnumeric i Kspread. 2. Integrisana programska okruženja koja se mogu koristiti i za modelovanje, u koje spadaju na primer: R, IDL, MATLAB, Octave i druga. 71
73 3. Programski jezici koji se mogu koristiti i za modelovanje, u koje spadaju na primer: C++, BASIC, PASCAL, FORTRAN, VB i JAVA. 4. Specijalizovana programska okruženja za modelovanje, u koje spadaju na primer: MODELMAKER, POWERSIM, SIMILE, STELLA i VENSIM. 5. Usko specijalizovni programi za ekološko modelovanje, u koje spadaju na primer: AEROMOD View, EcoRisk View, IRAP-h View, SVOffice, SADA, FRAMES i drugi. 6. Alati za modelovanje u okviru GIS programa, obuhvataju dodatke za GIS programe koji se mogu koristiti za ekološko modelovanje. 1. Programi za rad sa tabelama Činjenica je da je rad sa programima koji koriste tabele mnogo lakši nego, na primer, korišćenje programskih jezika. Programi za rad sa tabelama su široko rasprostranjeni u primeni, što znači da su poznati velikom broju korisnika. Većina ovih programa poseduje određene dodatke koji omogućavaju vizuelizaciju podataka ili statističku analizu. Njihova primena u ekološkom modelovanju je često vezana za populacionu ekologiju i konzervacionu biologiju. Iako postoji veliki broj korisnika koji može da se služi ovim programima, oni poseduju suštinska ograničenja koja predstavljaju veliki problem kad je potrebno konstruisati kompleksniji i sofisticiraniji ekološki model i kada je za dostizanje pravog rešenja potrebno vršiti iteraciju. Pored toga ovi programi ne podstiču strukturni pristup prilikom formiranja ekoloških modela. 2. Integrisana programska okruženja koja se mogu koristiti i za modelovanje Integisana programska okruženja predstavljaju kompleksne programske pakete koji se, na osnovu svojih funkcija, koriste u različitim oblastima. Na primer, programski paket R je moćan alat za statističku obradu, dok se MATLAB veoma puno koristi u primenjenoj matematici. Međutim, s obzirom na veliki broj opcija i funkcija, kao i mogućnost rešavanja kompleksnih problema, koje ovakva vrsta programskih paketa poseduje, oni su našli svoju primenu i u ekološkom modelovanju. Jedan od takvih primera je i MATLAB koji se primenjuje za modelovanje različitih ekoloških procesa biološke, fizičke i hemijske prirode. Postoji jako veliki broj ovakvih procesa koji se mogu modelovati uz pomoć MATLAB-a, a neki od njih su: reprodukcija organizama, radioaktivni raspad elemenata, hemijske transformacije polutanata u životnoj sredini, difuzija, disperzija, sorpcija, kinetičke i termodinamičke reakcije i mnogi drugi procesi. U programu MATLAB se ovakvi procesi predstavljaju matematičkim terminima. Taj pristup često dovodi do upotrebe diferencijalnih jednačina koje služe za predstavljanje promene različitih uslova u kojima se nalaze određene promenljive, kao što su koncentracija nekog polutanta ili gustina određene populacije, u prostoru i vremenu. Generalno, cilj je da se osnovni koncepti određenog ekološkog problema transformišu u matematičke formulacije. 3. Programski jezici koji se mogu koristiti za modelovanje Ogromna većina modela realnih problema se konačno predstavlja u vidu programa za računar. U tom smislu je potrebno izvršiti izbor odgovarajućeg programskog jezika koji je najviše prilagođen modelu. Međutim, izbor programskog jezika je najčešće diktiran njegovom raspoloživošću. Vrlo često postoje standardni programski paketi koji se mogu direktno koristiti za rešavanje modela kao što je program Microsoft Project (rešava probleme Simplex, PERT, CPM itd. metoda). Programski jezici za programiranje predstavljaju još jednu opciju kojom se mogu napraviti ekološki modeli. Programski jezici se inače koriste za izradu programa određene namene. Iako oni zahtevaju poznavanje komplikovanih komandi, gramatike i sintakse, vezanih za određeni programski jezik, ali može se reći da oni pružaju najveću fleksibilnost prilikom izrade ekoloških modela. 72
74 Postoji više različitih programskih jezika koji se mogu efikasno koristiti za ekološko modelovanje. Neki od njih, kao što su Basic i Fortran, su relativno jedonostavniji za savladavanje, dok drugi, kao što su C++ i Java, zahtevaju daleko više znanja i veštine kako bi se adekvatno primenjivali. Olakšavajuća okolnost je što dosta programskih jezika koji se trenutno primenjuju ima sličan set osnovnih komandi, pa će poznavanje jednog često značiti lakše snalaženje u nekom drugom programskom jeziku. Bez obzira o kom programskom jeziku se radi princip izrade modela se zasniva na prevođenju određenog ekološkog problema ili sistema u određeni programski jezik. Ovaj proces se donekle može uporediti sa prevođenjem sa jednog jezika na drugi. Imajući to u vidu jasno je da se obično za konkretnu situaciju obično mogu naći više tačnih rešenja. Kao krajnji rezultat dobija se gotov program pomoću koga se vrši modelovanje određenog ekološkog fenomena, procesa ili sistema. Ovakve gotove, napisane programe mogu koristiti i drugi korisnici koji ne moraju da poznaju programske jezike, već je samo dovoljno da unesu ulazne parametre vezane za specifičnu problematiku. Glavno ograničenje primene programskih jezika je vreme koje je potrebno da bi se jedan programski jezik savladao na adekvatan način i u dovoljnoj meri da se može primenjivati za ekološko modelovanje. Pored toga sam proces pisanja programa i ispravaljanja grešaka je isto veoma vremenski zahtevan. 4. Specijalizovana programska okruženja za modelovanje Specijalizovana programska okruženja za modelovanje su programski paketi čija je osnovna namena modelovanje različitih fenomena, procesa ili sistema, pa se samim tim mogu primenjivati i za ekološko modelovanje. Oni pružaju veliki broj važnih pogodnosti, od kojih je najznačajnija mogućnost konstruisanja modela uz pomoć grafičkog interfejsa pravljenjem dijagrama. Osim toga u okviru ovih programskih paketa nalazi se veliki broj ugrađenih analitičih i numeričkih funkcija, kao i opcija za vizuelizaciju podataka. Njihova glavna prednost je da formalizuju proces modelovanja unutar svog programskog okvira. Prvaljenje modela i modelovanje se u ovakvim programima odvija po principu koji je veoma sličan upravo vrsti metodologije ekološkog modelovanja koja je opisana u ovom tekstu. Nakon što se (definiše identifikuje) određeni ekološki problem prisupa se izradi konceptualnog modela, što se u ovoj vrsti programa izvodi crtanjem dijagrama uz pomoć odgovarajućih alata. Nakon toga se pomoću sakupljenih podataka i pretpostavki formiraju matematičke veze između pojedinih elemenata dijagrama koji predstavljaju određene ekološke entitete. Na osnovu tako formiranog modela program obavlja simulaciju i daje rezultate. Ovakvi programski paketi sadrže specijalne alate koji olakšavaju svaki od ovih koraka u metodologiji modelovanja. Glavna mana ovih programa je da u određenoj meri ograničavaju proces modelovanja svojim formalističkim pristupom. Ekološki entiteti se u ovim programima predstavljaju kao određene rezerve (npr. broj stabala u šumi), čija se promena u vremenu prikazuje putem tokova (npr. broj stabala posečenih u toku jedne godine). Problem je što se ne mogu svi ekološki problemi tretirati na ovaj način, pogotovo kada je potrebno prikazati prostorne promene. Bez obzira na svoja ograničenja specijalizovana programska okruženja sve više nalaze primenu u raznovorsnim problemima koji su vezani za životnu sredinu. 5. Usko specijalizovni programi za ekološko modelovanje Kako se vremenom modelovanje sve više razvijalo, shvaćeno je da se mnogi ekološki problemi mogu predstaviti i rešiti upravo uz pomoć modelovanja. To je dovelo do nastanka prvih programa koji su bili usko specijalizovani za rešavanje određenog ili više sličnih ekoloških problema. Ovi programi su se često zasnivali na statističkoj obradi podataka. Kasnije se, naglim razvojem ekološkog menadžmenta, ukazala potreba da modeli pruže podršku u odlučivanju i odabiru najbolje moguće alternative. Usled toga se formira nova grana ekološkog modelovanja koja se bavi menadžmentskim modelima za donošenje odluka. Paralelno sa njima razvijali su 73
75 se i naučni modeli koji su sve bolje oponašali fizičke, hemijske i biološke procese (kao što su dinamika fluida ili biogeohemija) i reprezentovali celokupne sisteme vezane za životnu sredinu. Njihova glavna uloga je bila sticanje novih saznanja i predviđanje na osnovu poznatih parametara. Danas postoji veliki broj programa koji se veoma detaljno bave određenim problemom vezanim za životnu sredinu. Oni obično poseduju veliki broj korisnih alata i već postojeće baze podataka vezane za problematiku kojom se specifični program bavi. Pored toga obično podržavaju i prostornu komponentu. Primer takvih programa su AEROMOD View koji se koristi za modelovanje zagađenja vazduha, ili EcoRisk View koji ima primenu u proceni rizika u životnoj sredini. Ovakva uska specijalizacija, ovakvih programa, na određeni ekološki problem je svakako pozitivna prilikom izučavanja tog problema. Međutim, s obzirom na njihovu različitost, poznavanje funkcija i alata u jednom programu obično nije od velike pomoći prilikom rada u programu koji se bavi drugačijim ekološkim modelom. 6. Alati za modelovanje u okviru GIS programa Razvojem geografskih informacionih sistema, a i pratećih tehnologija kao što je daljinska detekcija, postoji sve više geografskih baza podataka sa obilnim informacijama o životnoj sredini (na primer, pošumljenost terena, digitalni elevacioni model). Relativno skoro je shvaćeno da se ovi podaci mogu koristiti i za ekološko modelovanje, pa su u skladu sa tim počeli da se pojavljuju posebni alati, u obliku dodataka za postojeće GIS programske pakete, koji se mogu koristi u te svrhe. Njihova glavna prednost je prostorna kompontneta. Odnosno često se koriste za prikazivanje eventualnih promena na nekoj teritoriji u zavisnosti od vrste potencijalnog korišćenja tog prostora. Pored toga mogu se koristiti i za prostorno prikazivanje kretanja i transformacija zagađujućih materija u životnoj sredini Verifikacija računarskog modela (testiranje programa) Ocena rezultata dobijenih simulacijom na računaru Nakon što se određeni ekološki model u potpunosti formira i zatim izvrši njegova implementacija u okviru odabranog programskog paketa, vrši se njegova simulacija pomoću računara, čime se ujedno i vrši provera da li uopšte model funkcioniše. Prilikom pravljenja modela postoji veliki broj mogućih grešaka koje će imati takav efekat da uopšte neće moći da se obavi simulacija modela. Kada se takve greške isprave, ako uopšte i postoje, može se pristupiti oceni rezultata dobijenih simulacijom modela. Prva provera rezultata ima za cilj da se ustanovi da li se rezultati uopšte nalaze u okviru mogućih vrednosti. Ukoliko su dobijeni rezultati nemogući može se zaključiti da je došlo do neke veće greške tokom izrade modela, matematičke formulacije i/ili računarske implementacije, pa je potrebno detaljno preispitati model i ispraviti sve greške. Treba izvršiti poboljšanje i korekciju modela, tj. treba uraditi ispravke u pretpostavkama ili/i u modelu ili/i u algoritmu i ponovne simulacije. Ako se rezultati nalaze u okviru mogućih vrednosti pristupa se drugoj proveri modela koja se sastoji od verifikacija i validacije. Verifikacijom računarskog modela se proverava da li računarski model (program) verno predstavlja matematički model. Testiranje programa se svodi na formalnu verifikaciju ispravnog rada programa sa odgovarajućim test podacima. S obzirom da složeni modeli imaju programe sa više hiljada pa i desetine hiljada programskih naredbi, problem kreiranja konkretnih programa odnosno njihovog testiranja može biti izuzetno složen zadatak. 74
76 U ovoj fazi se prikupljaju podaci potrebni kako za testiranje programa u prethodnoj fazi tako i za praktičnu primenu modela u fazi implementacije. Problem tačnosti ulaznih podataka je značajan za konačnu validnost modela. Međutim, zahtevana tačnost nije ista za sve ulazne podatke. Rezultati modela mogu biti više osetljivi na promene nekih podataka, a manje na promene drugih. Analogno tome, potrebno je voditi računa i o zahtevanoj tačnosti ulaznih podataka Validacija (vrednovanje) modela realnog sistema Validacijom (vrednovanjem) modela se proverava da li model verno (uspešno) predstavlja realni sistem (da li je model dovoljno dobra apstrakcija realnog sistema), odnosno proverava se podudarnost bitnih karakteristika realnog sistema (predmeta modelovanja) i modela. Proverava se da li se rezultati istraživanja na modelu slažu sa rezultatima istraživanja na realnom sistemu, koji su dobijeni opservacijom (posmatranjem) ili eksperimentalno. U tom smislu potrebno je proveriti konzistentnost, osetljivost i primenljivost modela. Кonzistentnost modela se proverava tako što se provarava da li su rezultati logični pri promeni parametara modela do ekstremnih vrednosti. Osetljivost modela, se proverava na male promene ulaznih podataka. Ovaj korak obično uključuje numeričko eksperimentisanje na modelu. Na taj način se zaključuje o osetljivosti modela na pojedine ulazne podatke odnosno može se zaključivati o zahtevanoj tačnosti ulaznih podataka i tačnosti rezultata modela. Ako rezultati zadovoljavaju onda su ciljevi modelovanja ostvareni. Odabir reprezentativnih rezultata, poređenjem sa eksperimentima, detekcija uzroka greške. Prenos saznanja (rezultata) sa modela na realni sistem (predmet modelovanja), predstavlja inverzno preslikavanje u odnosu na formiranje modela. Model se testira (ispituje) u istim, sličnim ili analognim situacijama prema kojima je i formiran. Eksperimentisanje na modelu i prikupljanje podataka se izvodi primenom eksperimentalne metode i neophodne opreme, ako je predmet eksperimenta matematički model, onda se ova aktivnost svodi na simulaciju na računaru. Zaključci i preporuke Praktična primena (implementacija) modela. Uvođenje modela u praktičnu primenu je konačna faza izrade modela i očigledno kritična za konačan uspeh modela. Uspeh ove faze veoma zavisi od kooperacije korisnika modela. 75
77 9. RIZIK 9.1. Pojam rizik Rizik podrazumeva potencijalnu opasnost po ljude i materijalna dobra. Rizik se može posmatrati kao funkcija verovatnoće nastanka nekog neželjenog događaja i negativnih posledica koje može uzrokovanih taj neželjeni događaj (opasnosti po živote i zdravlje ljudi i životinja, životnu sredinu i materijalna dobra itd.): gde je: R - rizik R = f(v, P) V - verovatnoća nastanka neželjenog događaja P negativne posledice koje može uzrokovati neželjeni događaj Rizik se može smanjiti smanjenjem verovatnoće nastanka neželjenog događaja V ili smanjenjem negativnih posledica koje može uzrokovati neželjeni događaj P ili smanjujem i jednog i drugog. Pod pojmom rizik podrazumeva se verovatnoća (mogućnost) nastanka nekog neželjenog događaja koji može uzrokovati različite negativne posledice (kao što su: opasnosti po živote i zdravlje ljudi i životinja, materijalna dobra i životnu sredinu, opasnost od novčanih gubitaka u poslovanju i sl.). Postoje različite vrste rizika, kao što je: zdravstveni, finansijski, tehnološki, ekološki itd. Rizik može biti: nepredvidivi i predvidiv Postavljanjem pitanja "Koliki je rizik?", realno se postavljaju tri pitanja: Koji neželjeni događaj se može dogoditi? Koliko često se dešava taj neželjeni događaj? Ukoliko se dogodi taj neželjeni događaj kakve negativne posledice može uzrokovati? Pod pojmom rizik od šumskog požara podrazumeva se verovatnoća da na određenom prostoru pod šumom nastane požar, koji može uzrokovati različite negativne posledice (koje mogu biti materijalne i nematerijalne, kao što su npr.: izgorela drvna masa, ekološke posledice, posledice po atmosferu, biosveru i hidrosferu, životinjski svet, narušavanje performansi sistema, ugrožavanje materijalnih i prirodnih dobara, bezbednosti i zdravlja ljudi, narušavanje ekološke ravnoteže, odnosno odstupanje od stalnih kvaliteta sistema i unapred definisanih vrednosti Procena rizika Procena rizika je veoma subjektivan proces. Međutim, ako se pridržava određenih principa, prilikom procene rizika subjektivnost se može smanjiti na najmanji mogući nivo. S obzirom kriterijume na osnovu kojih se vrši procena rizika, metode koje se koriste za procenu rizika se mogu podeliti na: kvantitativne i kvalitativne. Procena rizika nekog neželjenog događaja se može vršiti na osnovu: 76
78 kvantitavne ili kvalitativne procene verovatnoće nastanka tog neželjenog događaja (tabela 6.1) i kvantitavno ili kvalitativno procene negativnih posledica (šteta) koje može uzrokovati taj neželjeni događaj (tabela 6.2). Tabela 6.1. Procena verovatnoća nastanka neželjenog događaja Tabela 6.2. Procena negativnih posledica koje može uzrokovati neželjeni događaj Pravilan izbor metode procene rizika omogućava da se primene adekvatne mere koje će obezbediti bezbednije radno mesto i radnu okolinu, kao i manju verovatnoća da može doći do profesionalnih oboljenja i povreda zaposlenih. Procena rizika na radnom mestu je sistematsko evidentiranje i procenjivanje svih opasnosti u procesu rada koji mogu uzrokovati nastanak povreda na radu, oboljenja ili oštećenja zdravlja i utvrđivanje mogućnosti, odnosno načina sprečavanja, otklanjanja ili smanjenja rizika. Procena rizika je prevashodno empirijski proces donošenja inženjerskih odluka na osnovu znanja i iskustva u cilju povišenja bezbednosti i zdravlja na radu. Pristup upravljanja rizikom podrazumeva njegovu identifikaciju, procenu i kontrolu. Postoje tri mogućnosti delovanja koje nisu međusobno isključive: smanjenje rizika, prenos rizika, prihvatanje rizika. Smanjenje rizika predstavlja proces u kojem se na osnovu sprovedene analize rizika nastoje sprovesti odgovarajuće protivmere i uvesti sigurnosni nadzor da bi se zaštitili resursi organizacije. U tom postupku nastoji se smanjiti verovatnoća opasnosti i/ili njen uticaj na proces. 77
79 Ukoliko se pokaže isplativijim, rizik je moguće preneti na treću stranu (npr. osiguravajuće društvo). Isto tako moguće je da implementacija protivmera ili prenos rizika nisu isplativi. U tom slučaju preduzeće može odlučiti da prihvati rizik, odnosno troškove koji iz toga proizilaze. Jedini pristup koji u upravljanju rizikom nije prihvatljiv je ignorisanje ili zanemarivanje rizika. Treba znati da je upravljanje rizikom kontinualan proces te da se odnos vrednosti resursa, ranjivosti i opasnosti s vremenom menja. Procena rizika od zagađenja životne sredine obuhvata: Identifikaciju opasnosti (hazarda), identifikacija negativnih posledica (efekata) koje zagađujuća susptanca može uzrokovati i Određivanje doze (primljenu koncentraciju zagađivača) i procena očekivanih efekata (odgovora na intoksikaciju) što obuhvata odnos unete doze koja je u funkciji od izloženosti (ekspozicije) i pojave, odnosno ozbiljnosti, negativnih efekata Kvantitativne metode procene rizika Kvantitativni kriterijumi procene rizika koriste numeričke vrednosti kako bi opisali verovatnoću i posledice događaja. Kvantitativna procena rizika znači predstavlja konačnu, tačnu brojnu vrednost rizika. Primeri za ovakvu procenu u oblasti bezbednosti i zdravlja na radu mogu biti vezani za procenu rizika od buke i drugih fizičkih ili hemijskih štetnosti i slično gde je jasno određen nivo dozvoljenog izlaganja, kao i povećanog izlaganja. Da bi se definisale verovatnoće i posledice kao brojne vrednosti neophodno je sprovesti dublje analize, posedovati odgovarajuće statističke podatke o akcidentima itd., što predstavlja suviše složen proces za masovniju primenu pa je u oblasti bezbednosti i zdravlja na radu prioritet dat kvalitativnoj proceni rizika, dok se kvantitativna primenjuje pre svega u slučajevima visokih rizika. Međutim treba napomenuti da najnovija iskustva i preporuke razvijenih zemalja EU ukazuju na to da bi kvantitativnu procenu rizika trebalo uvesti gde je god moguće i dati joj mnogo veći značaj i primenu. Postoji već i niz novih obrazaca, preporuka i tabela koje ukazuju na koji način se može relativno efikasno i jednostavno vršiti kvantitativna procena rizika u oblasti bezbednosti i zdravlja na radu. Tako su recimo sve posledice unifikovano izražene preko broja izgubljenih radnih dana i postoje razrađene tabele i uputstva za to. Kvantitativna analiza podrazumeva iskazivanje rizika u očekivanim novčanim troškovima na godišnjem nivou. Neke organizacije preferiraju ovakav način analize pošto im je tako omogućeno planiranje novčanih sredstava, a upravi se omogućava da bez tehničkih pojedinosti može doneti odgovarajuće odluke. Pri tom treba imati na umu da vrednost nekih resursa nije uvek moguće iskazati novčano, a kao rezultat toga mogu se pojaviti i brojke koje ne predstavljaju stvarno stanje. Metode koje se koriste u proceni rizika su često kvantitativne, mada stepen zahtevanog ulaska u detalje za pripremu procene zavisi od specifične aplikacije. Analiza frekventnosti se koristi za procenu verovatnoće svakog identifikovanog neželjenog događaja. Postoje tri opšta pristupa koja se upotrebljavaju za određivanje frekventnosti događaja: korišćenje relevantnih istorijskih podataka, izvođenje pomoću analitičkih ili simulacionih tehnika, korišćenje ekspertne procene. 78
80 Potpuna kvantitativna procena nije uvek moguća u slučaju nedostatka informacija o sistemu ili aktivnostima koje se analiziraju, nepotpunih podataka o otkazima, uticaju ljudskog faktora itd. Neki elementi rizika ne mogu da se kvantifikuju verovatnoćom distribucije. Njihov značaj se onda procenjuje kvantitativno razmatranjem prirode onoga što se štiti (ljudstvo, okolina), ozbiljnošću povreda ili oštećenja (neznatno, ozbiljno, katastrofalno) ili stepenom štete (jedna ili više osoba). Takođe treba napomenuti da se veličina nastale štete može definisati različito u zavisnosti od situacije. Analiza posledica procenjuje verovatnoće uticaja ukoliko se neželjeni događaj desi tj. procenjuje uticaj na ljude, okolinu ili imovinu. Posledice različitog tipa rizika se generalno izražavaju sigurnosnim (npr. fatalno, štetno), zdravstvenim, finansijskim, ekološkim terminima. Predviđanje posledica obično je posao za eksperte iz oblasti u kojoj je identifikovana moguća opasnost. Konačno, rizik se mora izraziti u odgovarajućoj formi. Neki od najčešće korišćenih izlaznih formi u proračunu rizika su: frekvencija nasuprot posledica, statističko očekivanje gubitaka u funkciji ekonomskih troškova itd. Kvantitativna procena rizika se vrši tako što se verovatnoća nastanka neželjenog događaja pomnoži sa posledica uzrokovanih tim neželjenim događajem: gde je: R - rizik R = V P V - verovatnoća nastanka neželjenog događaja P negativne posledice koje može uzrokovati neželjeni događaj pri čemu je potrebno da oba uticajna faktora (verovatnoća i negativne posledice) budu iskazane kao brojne vrednosti. U tom slučaju je i rezultujući rizik brojna vrednost odnosno rizik je potpuno kvantifikovan. Uglavnom se verovatnoća događaja prestavlja kao njegova učestalost po jedinici vremena ili aktivnost, dok su posledice predstavljene kao brojčani gubitak (finansijski, izgubljeni radni dani i sl.). Metodologija se odvija u sledećim koracima: Adresiranje svakog neželjenog događaja (rizične situacije) na osnovu pojedinačnih formi za određivanje rizika. Determinisanje kvantitativne vrednosti verovatnoće pojave neželjenog događaja P na podesan način i na osnovu realnog kriterijuma. Verovatnoća se izražava kao decimalni broj od 0 do 1, pri čemu 0 označava nemoguć događaj, a 1 događaj koji će se realizovati sa verovatnoćom 100%. U tabeli 6.2 prikazani su tipični kriterijumi za ustanovljavanje kvantitativnih vrednosti verovatnoća. Determinisanje kvantitativnih vrednosti posledica pojave svakog neželjenog događaja P na podesan način i na osnovu realnog kriterijuma. U tabeli 6.2 prikazani su tipični kriterijumi za ustanovljavanje kvantitativnih vrednosti posledica. Korišćenjem formule: R = V P, determiniše se faktor rizika za svaki identifikovani neželjeni događaj. Na osnovu dobijenih vrednosti određuje se nivo rizika za svaki identifikovani neželjeni događaj. 79
81 Kvalitativne metode procene rizika Kvalitativna analiza rizika predstavlja subjektivniji pristup pri kojem se resursi, rizici i protivmere posmatraju relativno s obzirorn na sistem. Za sprovođenje kvalitativne analize nije potrebno egzaktno poznavanje materijalnih vrednosti pojedinih resursa, već je za njihovo vrednovanje potrebno poznavati važnost za pojedine poslovne procese. Rezultat kvalitativne analize iskazuje samo relativan odnos vrednosti šteta nastalih delovanjem neke opasnosti i uvođenja protivmera. Pri tome treba imati na umu da je ta procena subjektivne prirode, te je stoga podložna greškama. Kvalitativne metode za procenu rizika baziraju se na osnovu ličnog iskustva i rasuđivanja učesnika u timu za procenu rizika i/ili korišćenju raspoloživih kvalitativnih, nenumeričkih podataka. Ovakav pristup ne zahteva podatke o prethodnim štetnim događajima, uzrocima i posledicama, ali uslovljava da krajnji rezultat procene rizika bude opisno, kvalitativno iskazana veličina rizika (npr. visoki rizik, umereni rizik i sl.). Kako bi opisali verovatnoću nastanka nekog neželjenog događaja kvalitativni kriterijumi procene rizika koriste reči kao što su: retko, neverovatno, moguće, verovatno ili skoro sigurno ili verovatno, moguće, često, retko. Kako bi opisali negativne posledice koje može biti uzrokovati neki neželjeni događaj kvalitativni kriterijumi procene rizika koriste reči kao što su: kobne, ozbiljne, male ili zanemarljive ili neznatno, katastrofalno itd. U kvalitativnim metodama za procenu rizika najčešće se koriste subjektivni kriterijumi, koji se mere u kvalitativnim skalama. Procena je subjektivne prirode pa je zbog toga podložna greškama. U praksi se optimalno koriste kvalitativne skale sa tri do sedam kvalitativna opisa, što zahteva izražen stručni pristup analizi potencijalnih opasnosti/štetnosti. Metode sa manje od tri kvalitativna opisa za faktore rizika nisu zanimljive, jer nisu precizne, a sa više od sedam dovode do značajnih poteškoća subjektivnog karaktera, povezanih sa nemogućnošću učesnika u timu za procenu rizika da dosta precizno prepozna kvalitativni opis faktora rizika. 1. Metoda matrice rizika Procena rizika kvalitativnim metodama podrazumeva korišćenje nenumeričkih, odnosno kvalitativno opisanih podataka. U kvalitativne metode za procenu rizika spada i metoda matrice rizika (matrica za rangiranje rizika). Rangiranje rizika se zasniva na matrici, koja za svoje ose ima rangove posledice i rangove verovatnoće. Učesnici u timu za procenu rizika često koriste u radu matricu rizika za uspostavljanje logičke povezanosti posledica i verovatnoće u procenjivanju rizika za prethodno identifikovane opasnosti/štetnosti. Takođe, koriste se kao jednoobrazno definisan način određivanja stepena, odnosno nivoa pojedinih rizika koji se procenjuju. Matrica rizika (slika 34) se formira tako što se na x-osu nanose rangovi verovatnoće (korak 1), a na y-osu rangovi posledica (korak 2) i zatim određuje rang rizika (korak 3). 80
82 Slika 34. Formiranje matrice rizika Tipične kvalitativne metode za procenu rizika su: matrica rizika 4 6 (MIL-STD-882C), matrica rizika 5 5 (AS/NZS 4360: 2004) i matrica rizika 3 3 (OHSAS standard). Metoda matrice rizika započinje dodeljivanjem kvalitativnih vrednosti verovatnoćama događaja i posledica koje se kasnije koriste pri determinisanju kvalitativnog faktora rizika. Ključne karakteristike ovog metoda su da: omogućava nezavisno određivanje verovatnoća i posledica rizika i obezbeđuje kvalitativno definisanje rizika i njegove težine Metodologija se odvija u sledećim koracima: Adresiranje svakog neželjenog događaja (rizične situacije) na osnovu pojedinačnih formi za određivanje rizika. Determinisanje kvalitativnih vrednosti verovatnoće nastanka neželjenog događaja V na podesan način i na osnovu realnog kriterijuma. U tabeli 6.1. prikazani su tipični kriterijumi za ustanovljavanje kvalitativnih vrednosti verovatnoća. Determinisanje kvalitativnih vrednosti posledica pojave svakog neželjenog događaja P na podesan način i na osnovu realnog kriterijuma. U tabeli 6.2 su prikazani tipični kriterijumi za ustanovljavanje kvalitativnih vrednosti posledica. Određivanje nivoa rizika na bazi preseka kvalitativnih vrednosti za verovatnoće nastanka neželjenog događaja V i posledica uzrokovanih tim neželjenim događajem P u matrici rizika 5 4 prikazano je u tabeli 6.3. Tabela 6.3. Matrica rizika 81
83 U zavisnosti od aktivnosti i sposobnosti da se izdiferencira nivo rizika, mogu se konstruisati matrice različitih nivoa rizika. Na primer u tabeli 6.3. izvršena je kategorizacija na tri nivoa rizika (nizak, srednji i visok) Identifikacija opasnosti Opasnost se može definisati kao skup uslova koji mogu uzrokovati neki neželjeni događaj (povred e ili štete). Opasnost može biti različitog porekla prirodna, tehnološka (strukture), sociološka (rat), način života (pušenje). Identifikacija opasnosti i scenarija opasnosti je od krucijalnoj značaja za analizu rizika, zahteva detaljno ispitivanje i razumevanje sistema, sa razvojem tehnologija dobija na složenosti. Cilj analize i broj raspoloživih informacija o sistemu treba da upute na izbor adekvatne metode procene rizika. Kada se izabere metoda procene rizika, onda treba identifikovati opasnosti i opisati moguće sekvence neželjenih događaja i faktore koji mogu dovesti do toga. Metoda determiniše proces identifikacije opasnosti. Neke od metoda su kvalitativne, dok druge mogu da pruže i kvantitativnu estimaciju. Postoje dva različita pristupa analizi i identifikaciji opasnosti: indukcioni i dedukcioni. Indukcioni pristup se zasniva na razmatranju od pojedinačnog slučaja do generalnog zaključivanja, dok dedukcioni ide u suprotnom smeru od generalnog do specifičnog. U globalu, induktivne metode se primenjuju da determinišu koja su stanja sistema moguća, počev od inicijalnog događaja - definišu se posledice. Deduktivne metode se koriste da determinišu kako posmatrano stanje može da se realizuje počev od neželjenog događaja-definišu se uzroci. PHA (Preliminary Hazard Analisys) je gruba induktivna i kvalitativna metoda za identifikaciju potencijalne opasnosti. Liste praćenja potencijalnih opasnih elemenata i situacija pružaju pomoć pri sprovođenju PHA. Za uspešno izvođenje analize neophodno je formiranje tima sastavljenog od eksperata koji su "familijarni" sa datim sistemom. Svaki identifikovani neželjeni događaj se posebno analizira kako bi se opisali mogući uzroci, posledice i verovatnoće. Posledice mogu takođe biti izdvojene npr. u one koje imaju uticaja na okolinu, zdravlje ljudi i ekonomiju i shodno tome se različito ocenjuju. Nakon toga, posledice i verovatnoće se rangiraju prema svojoj težini. Analiza proizvodi preliminarni kvalitativni dokument o mogućim neželjenim događajima s obzirom na identifikovane izvore rizika. 82
Slide 1
 Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
PowerPoint Presentation
 ТЕХНОЛОШКО ПРЕДВИЂАЊЕ Развој научног предвиђања Најзначајнија промена метода и техника се везује за појаву НАУЧНОГ предвиђања. Историјско-библиографски метод (са вештине на науку) Три фазе: 1. Религијска
ТЕХНОЛОШКО ПРЕДВИЂАЊЕ Развој научног предвиђања Најзначајнија промена метода и техника се везује за појаву НАУЧНОГ предвиђања. Историјско-библиографски метод (са вештине на науку) Три фазе: 1. Религијска
Slide 1
 Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 1: Увод и историјски развој теорије система UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES Катедра за управљање системима Наставници:
Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 1: Увод и историјски развој теорије система UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES Катедра за управљање системима Наставници:
Modeliranje i Simulacija
 Modeliranje i simulacija dr Aleksandar Marković, red. prof. markovic.aleksandar@fon.bg.ac.rs Simulacija u poslovnom odlučivanju Metodologija istraživanja Realni sistem Rezultati Modelar (analitičar) Model
Modeliranje i simulacija dr Aleksandar Marković, red. prof. markovic.aleksandar@fon.bg.ac.rs Simulacija u poslovnom odlučivanju Metodologija istraživanja Realni sistem Rezultati Modelar (analitičar) Model
Istraživanje turističkog tržišta
 ISTRAŽIVANJE TURISTIČKOG TRŽIŠTA asistent:branislava Hristov Stančić branislava@ekof.bg.ac.rs Suština i sadržaj istraživanja tržišta Istraživanje tržišta istraživanje marketinga Istraživanje marketinga
ISTRAŽIVANJE TURISTIČKOG TRŽIŠTA asistent:branislava Hristov Stančić branislava@ekof.bg.ac.rs Suština i sadržaj istraživanja tržišta Istraživanje tržišta istraživanje marketinga Istraživanje marketinga
Microsoft Word - CAD sistemi
 U opštem slučaju, se mogu podeliti na 2D i 3D. 2D Prvo pojavljivanje 2D CAD sistema se dogodilo pre više od 30 godina. Do tada su inženjeri koristili table za crtanje (kulman), a zajednički jezik komuniciranja
U opštem slučaju, se mogu podeliti na 2D i 3D. 2D Prvo pojavljivanje 2D CAD sistema se dogodilo pre više od 30 godina. Do tada su inženjeri koristili table za crtanje (kulman), a zajednički jezik komuniciranja
Microsoft PowerPoint - IS_G_predavanja_ [Compatibility Mode]
![Microsoft PowerPoint - IS_G_predavanja_ [Compatibility Mode] Microsoft PowerPoint - IS_G_predavanja_ [Compatibility Mode]](/thumbs/103/157511151.jpg) INŽENJERSKE SIMULACIJE Aleksandar Karač Kancelarija 1111 tel: 44 91 20, lok. 129 akarac@ptf.unze.ba Nermin Redžić Kancelarija 4202 tel: 44 91 20, lok.128 nermin.redzic@ptf.unze.ba www.ptf.unze.ba http://ptf.unze.ba/inzenjerske-simulacije
INŽENJERSKE SIMULACIJE Aleksandar Karač Kancelarija 1111 tel: 44 91 20, lok. 129 akarac@ptf.unze.ba Nermin Redžić Kancelarija 4202 tel: 44 91 20, lok.128 nermin.redzic@ptf.unze.ba www.ptf.unze.ba http://ptf.unze.ba/inzenjerske-simulacije
Контрола ризика на радном месту – успостављањем система менаџмента у складу са захтевима спецификације ИСО 18001/2007
 Profesor: dr Biljana Gemović Rizik je termin usko povezan sa svim poslovnim i proizvodnim aktivnostima i njegovo postojanje kao takvo mora biti prepoznato i prihvaćeno. Standard OHSAS 18001:2007 rizik
Profesor: dr Biljana Gemović Rizik je termin usko povezan sa svim poslovnim i proizvodnim aktivnostima i njegovo postojanje kao takvo mora biti prepoznato i prihvaćeno. Standard OHSAS 18001:2007 rizik
PowerPoint Presentation
 Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Sa stanovišta pristupa problemu korišćenja kapaciteta, razlikuju se metode
Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Sa stanovišta pristupa problemu korišćenja kapaciteta, razlikuju se metode
РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена ) Прва година: ПРВА ГОДИНА - сви сем информатике Име пр
 РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена 23.01.2017.) Прва година: ПРВА ГОДИНА - сви сем информатике Име предмета Датум и термин одржавања писменог дела испита
РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена 23.01.2017.) Прва година: ПРВА ГОДИНА - сви сем информатике Име предмета Датум и термин одржавања писменог дела испита
God_Rasp_2015_ xls
 ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА, НОВИ САД Датум: 14.09.2016, Страна: 1 I I I 1 13 Грађевински материјали и конструкције I 28.01.2016 09.02.2016 31.03.2016 16.06.2016 04.07.2016 01.09.2016 15.09.2016 26.09.2016
ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА, НОВИ САД Датум: 14.09.2016, Страна: 1 I I I 1 13 Грађевински материјали и конструкције I 28.01.2016 09.02.2016 31.03.2016 16.06.2016 04.07.2016 01.09.2016 15.09.2016 26.09.2016
Inženjering informacionih sistema
 Fakultet tehničkih nauka, Novi Sad Inženjering informacionih sistema Dr Ivan Luković Dr Slavica Kordić Nikola Obrenović Milanka Bjelica Dr Jelena Borocki Dr Milan Delić UML UML (Unified Modeling Language)
Fakultet tehničkih nauka, Novi Sad Inženjering informacionih sistema Dr Ivan Luković Dr Slavica Kordić Nikola Obrenović Milanka Bjelica Dr Jelena Borocki Dr Milan Delić UML UML (Unified Modeling Language)
I година Назив предмета I термин Вријеме II термин Вријеме Сала Математика : :00 све Основи електротехнике
 I година Математика 1 2225 20.06.2019. 9:00 04.07.2019. 9:00 све Основи електротехнике 1 2226 17.06.2019. 9:00 01.07.2019. 13:00 све Програмирање 1 2227 21.06.2019. 9:00 05.07.2019. 9:00 све Основи рачунарске
I година Математика 1 2225 20.06.2019. 9:00 04.07.2019. 9:00 све Основи електротехнике 1 2226 17.06.2019. 9:00 01.07.2019. 13:00 све Програмирање 1 2227 21.06.2019. 9:00 05.07.2019. 9:00 све Основи рачунарске
I година Назив предмета I термин Вријеме II термин Вријеме Сала Математика : :00 све Основи електротехнике
 I година Математика 1 2225 05.09.2019. 9:00 19.09.2019. 9:00 све Основи електротехнике 1 2226 02.09.2019. 9:00 16.09.2019. 9:00 све Програмирање 1 2227 06.09.2019. 9:00 20.09.2019. 9:00 све Основи рачунарске
I година Математика 1 2225 05.09.2019. 9:00 19.09.2019. 9:00 све Основи електротехнике 1 2226 02.09.2019. 9:00 16.09.2019. 9:00 све Програмирање 1 2227 06.09.2019. 9:00 20.09.2019. 9:00 све Основи рачунарске
I година Назив предмета I термин Вријеме II термин Вријеме Сала Математика : :00 све Основи електротехнике
 I година Математика 1 2225 07.02.2019. 9:00 21.02.2019. 9:00 све Основи електротехнике 1 2226 04.02.2019. 9:00 18.02.2019. 9:00 све Програмирање 1 2227 08.02.2019. 9:00 22.02.2019. 9:00 све Основи рачунарске
I година Математика 1 2225 07.02.2019. 9:00 21.02.2019. 9:00 све Основи електротехнике 1 2226 04.02.2019. 9:00 18.02.2019. 9:00 све Програмирање 1 2227 08.02.2019. 9:00 22.02.2019. 9:00 све Основи рачунарске
Slide 1
 Statistička analiza u hidrologiji Uvod Statistička analiza se primenjuje na podatke osmatranja hidroloških veličina (najčešće: protoka i kiša) Cilj: opisivanje veze između veličine i verovatnoće njene
Statistička analiza u hidrologiji Uvod Statistička analiza se primenjuje na podatke osmatranja hidroloških veličina (najčešće: protoka i kiša) Cilj: opisivanje veze između veličine i verovatnoće njene
I година Назив предмета I термин Вријеме Сала Математика :00 све Основи електротехнике :00 све Програмирање
 I година Математика 1 2225 03.10.2019. 15:00 све Основи електротехнике 1 2226 30.09.2019. 15:00 све Програмирање 1 2227 04.10.2019. 15:00 све Основи рачунарске технике 2228 01.10.2019. 15:00 све Социологија
I година Математика 1 2225 03.10.2019. 15:00 све Основи електротехнике 1 2226 30.09.2019. 15:00 све Програмирање 1 2227 04.10.2019. 15:00 све Основи рачунарске технике 2228 01.10.2019. 15:00 све Социологија
Microsoft Word - Master 2013
 ИСПИТНИ РОК: ЈУН 2018/2019 МАСТЕР АКАДЕМСКЕ СТУДИЈЕ (АКРЕДИТАЦИЈА 2013) Студијски програм: ЕЛЕКТРОЕНЕРГЕТИКА Семестар 17.06.2019 Статички електрицитет у технолошким процесима Електронска кола за управљање
ИСПИТНИ РОК: ЈУН 2018/2019 МАСТЕР АКАДЕМСКЕ СТУДИЈЕ (АКРЕДИТАЦИЈА 2013) Студијски програм: ЕЛЕКТРОЕНЕРГЕТИКА Семестар 17.06.2019 Статички електрицитет у технолошким процесима Електронска кола за управљање
FAKULTET ORGANIZACIONIH NAUKA
 FAKULTET ORGANIZACIONIH NAUKA PRELIMINARNI RASPORED ISPITA ZA JANUARSKI ISPITNI ROK 2008. GODINE Predmet Od. P/U Datum Sala Napomena Akcionarstvo i berzansko poslovanje ME U 03.02.2008----10:00 201 Arhitektura
FAKULTET ORGANIZACIONIH NAUKA PRELIMINARNI RASPORED ISPITA ZA JANUARSKI ISPITNI ROK 2008. GODINE Predmet Od. P/U Datum Sala Napomena Akcionarstvo i berzansko poslovanje ME U 03.02.2008----10:00 201 Arhitektura
Microsoft Word - Master 2013
 ИСПИТНИ РОК: СЕПТЕМБАР 2018/2019 МАСТЕР АКАДЕМСКЕ СТУДИЈЕ (АКРЕДИТАЦИЈА 2013) Студијски програм: ЕЛЕКТРОЕНЕРГЕТИКА Семестар 19.08.2019 Електромагнетна компатибилност у електроенергетици Управљање дистрибутивном
ИСПИТНИ РОК: СЕПТЕМБАР 2018/2019 МАСТЕР АКАДЕМСКЕ СТУДИЈЕ (АКРЕДИТАЦИЈА 2013) Студијски програм: ЕЛЕКТРОЕНЕРГЕТИКА Семестар 19.08.2019 Електромагнетна компатибилност у електроенергетици Управљање дистрибутивном
MENADŽMENT LJUDSKIH RESURSA
 MENADŽMENT LJUDSKIH RESURSA Analiza posla ZAŠTO JE POTREBNO PLANIRANJE LJUDSKIH RESURSA? ZBOG MOGUĆNOSTI BLAGOVREMENOG PREPOZNAVANJA NEDOSTATAKA U POTENCIJALU KOMPANIJE ZBOG MOGUĆNOSTI DETEKTOVANJA SKRIVENIH
MENADŽMENT LJUDSKIH RESURSA Analiza posla ZAŠTO JE POTREBNO PLANIRANJE LJUDSKIH RESURSA? ZBOG MOGUĆNOSTI BLAGOVREMENOG PREPOZNAVANJA NEDOSTATAKA U POTENCIJALU KOMPANIJE ZBOG MOGUĆNOSTI DETEKTOVANJA SKRIVENIH
Microsoft Word - Smerovi 1996
 ИСПИТНИ РОК: СЕПТЕМБАР 2018/2019 СТАРИ НАСТАВНИ ПЛАН И ПРОГРАМ (1996) Смер: СВИ Филозофија и социологија 20.08.2019 Теорија друштвеног развоја 20.08.2019 Програмирање 20.08.2019 Математика I 21.08.2019
ИСПИТНИ РОК: СЕПТЕМБАР 2018/2019 СТАРИ НАСТАВНИ ПЛАН И ПРОГРАМ (1996) Смер: СВИ Филозофија и социологија 20.08.2019 Теорија друштвеног развоја 20.08.2019 Програмирање 20.08.2019 Математика I 21.08.2019
1
 Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Microsoft Word - Raspored ispita Jun.doc
 FAKULTET ORGANIZACIONIH NAUKA KONAČAN RASPORED ISPITA ZA JUNSKI ISPITNI ROK 8. GODINE Predmet Od. P/U Datum Sale Napomena Akcionarstvo i berzansko poslovanje ME U 21/06/8---- Arhitektura računara i oper.
FAKULTET ORGANIZACIONIH NAUKA KONAČAN RASPORED ISPITA ZA JUNSKI ISPITNI ROK 8. GODINE Predmet Od. P/U Datum Sale Napomena Akcionarstvo i berzansko poslovanje ME U 21/06/8---- Arhitektura računara i oper.
FAKULTET ORGANIZACIONIH NAUKA
 FAKULTET ORGANIZACIONIH NAUKA KONAČAN RASPORED ISPITA ZA OKTOBARSKI ISPITNI ROK (po datumu) Predmet Odsek P/U Datum Sala Upravljanje kvalitetom dokumentacije UK P 22/09/2007----09:00 RC Informacioni sistemi
FAKULTET ORGANIZACIONIH NAUKA KONAČAN RASPORED ISPITA ZA OKTOBARSKI ISPITNI ROK (po datumu) Predmet Odsek P/U Datum Sala Upravljanje kvalitetom dokumentacije UK P 22/09/2007----09:00 RC Informacioni sistemi
Универзитет у Београду Факултет организационих наука Распоред испита за предмете мастер академских студија Испитни рок: Јун Предмет Датум Време
 Универзитет у Београду Факултет организационих наука Распоред испита за предмете мастер академских студија Испитни рок: Јун 2018. Предмет Датум Време Сала Напомена Big data у електронском пословању 4.
Универзитет у Београду Факултет организационих наука Распоред испита за предмете мастер академских студија Испитни рок: Јун 2018. Предмет Датум Време Сала Напомена Big data у електронском пословању 4.
Microsoft PowerPoint - Topic02 - Serbian.ppt
 Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
KAKO BRŽE DO POSLA ZA StrukovnOG inženjerA zaštite životne sredine
 KAKO BRŽE DO POSLA ZA SPECIJALISTU STRUKOVNOG INŽENJERA ZAŠTITE ŽIVOTNE SREDINE Dr Vesna Marjanović, profesor Visoke poslovno-tehničke škole strukovnih studija, Užice Specijalističke strukovne studije
KAKO BRŽE DO POSLA ZA SPECIJALISTU STRUKOVNOG INŽENJERA ZAŠTITE ŽIVOTNE SREDINE Dr Vesna Marjanović, profesor Visoke poslovno-tehničke škole strukovnih studija, Užice Specijalističke strukovne studije
FAKULTET ORGANIZACIONIH NAUKA
 FAKULTET ORGANIZACIONIH NAUKA PRELIMINARNI RASPORED ISPITA ZA SEPTEMBARSKI ISPITNI ROK 2008. GODINE Predmet Od. P/U Datum Sal. Napomena Akcionarstvo i berzansko poslovanje ME U 29.08.2008----09:00 Institut
FAKULTET ORGANIZACIONIH NAUKA PRELIMINARNI RASPORED ISPITA ZA SEPTEMBARSKI ISPITNI ROK 2008. GODINE Predmet Od. P/U Datum Sal. Napomena Akcionarstvo i berzansko poslovanje ME U 29.08.2008----09:00 Institut
Microsoft Word - Akreditacija 2013
 07.10.2017 ОСНОВНЕ АКАДЕМСКЕ СТУДИЈЕ (АКРЕДИТАЦИЈА 2013) Модул: СВИ Година I Од II до IV Семестар I II IV-VIII Лабораторијски практикум - Увод у рачунарство Алгоритми и програмирање Математика 1 Математика
07.10.2017 ОСНОВНЕ АКАДЕМСКЕ СТУДИЈЕ (АКРЕДИТАЦИЈА 2013) Модул: СВИ Година I Од II до IV Семестар I II IV-VIII Лабораторијски практикум - Увод у рачунарство Алгоритми и програмирање Математика 1 Математика
ИСПИТНА ПИТАЊА ЗА ПРВИ КОЛОКВИЈУМ 1. Шта проучава биофизика и навести бар 3 области биофизике 2. Основне физичке величине и њихове јединице 3. Појам м
 ИСПИТНА ПИТАЊА ЗА ПРВИ КОЛОКВИЈУМ 1. Шта проучава биофизика и навести бар 3 области биофизике 2. Основне физичке величине и њихове јединице 3. Појам материјалне тачке 4. Појам механичког система 5. Појам
ИСПИТНА ПИТАЊА ЗА ПРВИ КОЛОКВИЈУМ 1. Шта проучава биофизика и навести бар 3 области биофизике 2. Основне физичке величине и њихове јединице 3. Појам материјалне тачке 4. Појам механичког система 5. Појам
Microsoft PowerPoint - Topic02 - Serbian.ppt
 Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
Microsoft Word - Akreditacija 2013
 ОСНОВНЕ АКАДЕМСКЕ СТУДИЈЕ (АКРЕДИТАЦИЈА 2013) Модул: СВИ Година I Од II до IV Семестар I II IV-VII 18.09.2017 Алгоритми и програмирање 19.09.2017 Математика 1 20.09.2017 Математика 2 21.09.2017 Увод у
ОСНОВНЕ АКАДЕМСКЕ СТУДИЈЕ (АКРЕДИТАЦИЈА 2013) Модул: СВИ Година I Од II до IV Семестар I II IV-VII 18.09.2017 Алгоритми и програмирање 19.09.2017 Математика 1 20.09.2017 Математика 2 21.09.2017 Увод у
Microsoft PowerPoint - vezbe 4. Merenja u telekomunikacionim mrežama
 Merenja u telekomunikacionim mrežama Merenja telefonskog saobraćaja Primer 1 - TCBH Na osnovu najviših vrednosti intenziteta saobraćaja datih za 20 mernih dana (tabela), pomoću metode TCBH, pronaći čas
Merenja u telekomunikacionim mrežama Merenja telefonskog saobraćaja Primer 1 - TCBH Na osnovu najviših vrednosti intenziteta saobraćaja datih za 20 mernih dana (tabela), pomoću metode TCBH, pronaći čas
Универзитет у Београду Факултет организационих наука Коначан распоред испита за предмете Мастер академских студија Испитни рок: ОКТОБАР Предмет
 Универзитет у Београду Факултет организационих наука Коначан распоред испита за предмете Мастер академских студија Испитни рок: ОКТОБАР 2016. Предмет Датум Време Сала Напомена Big data у електронском пословању
Универзитет у Београду Факултет организационих наука Коначан распоред испита за предмете Мастер академских студија Испитни рок: ОКТОБАР 2016. Предмет Датум Време Сала Напомена Big data у електронском пословању
Microsoft Word - Akreditacija 2013
 ИСПИТНИ РОК: ОКТОБАР 2 2017/2018 ОСНОВНЕ АКАДЕМСКЕ СТУДИЈЕ (АКРЕДИТАЦИЈА 2013) Модул: СВИ Година I Од II до IV Семестар I II IV-VIII Лабораторијски практикум - Алгоритми и програмирање Лабораторијски практикум
ИСПИТНИ РОК: ОКТОБАР 2 2017/2018 ОСНОВНЕ АКАДЕМСКЕ СТУДИЈЕ (АКРЕДИТАЦИЈА 2013) Модул: СВИ Година I Од II до IV Семестар I II IV-VIII Лабораторијски практикум - Алгоритми и програмирање Лабораторијски практикум
LAB PRAKTIKUM OR1 _ETR_
 UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA, TELEKOMUNIKACIJE I RAČUNARI PREDMET: OSNOVE RAČUNARSTVA 1 FOND ČASOVA: 2+1+1 LABORATORIJSKA VJEŽBA BROJ 1 NAZIV: REALIZACIJA
UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA, TELEKOMUNIKACIJE I RAČUNARI PREDMET: OSNOVE RAČUNARSTVA 1 FOND ČASOVA: 2+1+1 LABORATORIJSKA VJEŽBA BROJ 1 NAZIV: REALIZACIJA
Microsoft PowerPoint - SEP-2013-CAS02
 STRATEGIJE E ZA ELEKTRONSKO POSLOVANJE STRATEGIJE ZA ELEKTRONSKO POSLOVANJE Elektronsko poslovanje ne predstavlja samo dodatak tradicionalnom, već ono predstavlja revoluciju u poslovanju. Ono omogućava
STRATEGIJE E ZA ELEKTRONSKO POSLOVANJE STRATEGIJE ZA ELEKTRONSKO POSLOVANJE Elektronsko poslovanje ne predstavlja samo dodatak tradicionalnom, već ono predstavlja revoluciju u poslovanju. Ono omogućava
Microsoft Word - Akreditacija 2013
 ИСПИТНИ РОК: СЕПТЕМБАР 2018/2019 ОСНОВНЕ АКАДЕМСКЕ СТУДИЈЕ (АКРЕДИТАЦИЈА 2013) Модул: СВИ Година I Од II до IV Семестар I II IV-VII Лабораторијски практикум Физика Лабораторијски практикум - Увод у рачунарство
ИСПИТНИ РОК: СЕПТЕМБАР 2018/2019 ОСНОВНЕ АКАДЕМСКЕ СТУДИЈЕ (АКРЕДИТАЦИЈА 2013) Модул: СВИ Година I Од II до IV Семестар I II IV-VII Лабораторијски практикум Физика Лабораторијски практикум - Увод у рачунарство
STABILNOST SISTEMA
 STABILNOST SISTEMA Najvaznija osobina sistema automatskog upravljanja je stabilnost. Generalni zahtev koji se postavlja pred projektanta jeste da projektovani i realizovani sistem automatskog upravljanja
STABILNOST SISTEMA Najvaznija osobina sistema automatskog upravljanja je stabilnost. Generalni zahtev koji se postavlja pred projektanta jeste da projektovani i realizovani sistem automatskog upravljanja
Metode psihologije
 Metode psihologije opažanje, samoopažanje, korelacijska metoda, eksperiment Metode služe za istraživanja... Bez znanstvenih istraživanja i znanstvene potvrde, spoznaje i objašnjenja ne mogu postati dio
Metode psihologije opažanje, samoopažanje, korelacijska metoda, eksperiment Metode služe za istraživanja... Bez znanstvenih istraživanja i znanstvene potvrde, spoznaje i objašnjenja ne mogu postati dio
TEORIJA SIGNALA I INFORMACIJA
 Multiple Input/Multiple Output sistemi MIMO sistemi Ulazi (pobude) Izlazi (odzivi) u 1 u 2 y 1 y 2 u k y r Obrada=Matematički model Načini realizacije: fizički sistemi (hardware) i algoritmi (software)
Multiple Input/Multiple Output sistemi MIMO sistemi Ulazi (pobude) Izlazi (odzivi) u 1 u 2 y 1 y 2 u k y r Obrada=Matematički model Načini realizacije: fizički sistemi (hardware) i algoritmi (software)
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић
 Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Драган Пејић, Бојан Вујичић, Небојша Пјевалица,
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Драган Пејић, Бојан Вујичић, Небојша Пјевалица,
Slide 1
 Str. 9 UVOD Predavač: Dr Mirko Savić savicmirko@ef.uns.ac.rs www.ef.uns.ac.rs Dokazano je... Da li vama treba statistika? Top ten najboljih zanimanja (Blic, 6.3.2010.): 1. Aktuari 2. Softverski inženjeri
Str. 9 UVOD Predavač: Dr Mirko Savić savicmirko@ef.uns.ac.rs www.ef.uns.ac.rs Dokazano je... Da li vama treba statistika? Top ten najboljih zanimanja (Blic, 6.3.2010.): 1. Aktuari 2. Softverski inženjeri
Projektovanje tehnoloških procesa
 ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА Департман за производно машинство Пројектовање технолошких процеса Тема: Др Мијодраг Милошевић Технолошки процеси израде производа Део производног процеса у коме се врши измена
ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА Департман за производно машинство Пројектовање технолошких процеса Тема: Др Мијодраг Милошевић Технолошки процеси израде производа Део производног процеса у коме се врши измена
Satnica.xlsx
 САТНИЦА ПОЛАГАЊА ИСПИТА У ИСПИТНОМ РОКУ СЕПТЕМБАР 2018/2019 ПОНЕДЕЉАК 19.08.2019 Објектно оријентисано програмирање 41 2Б-ТЕЛ Методе преноса у телекомуникационим системима 1 2Б-ТЕЛ Моделовање и симулација
САТНИЦА ПОЛАГАЊА ИСПИТА У ИСПИТНОМ РОКУ СЕПТЕМБАР 2018/2019 ПОНЕДЕЉАК 19.08.2019 Објектно оријентисано програмирање 41 2Б-ТЕЛ Методе преноса у телекомуникационим системима 1 2Б-ТЕЛ Моделовање и симулација
Microsoft Word - vodicitm.doc
 Универзитет у Београду Машински факултет ВОДИЧ кроз основне академске студије Информационе технологије у машинству Школска 2019/2020. година Београд, октобар 2019. године Структура студија које се од 1.10.2005.
Универзитет у Београду Машински факултет ВОДИЧ кроз основне академске студије Информационе технологије у машинству Школска 2019/2020. година Београд, октобар 2019. године Структура студија које се од 1.10.2005.
ТРОУГАО БРЗИНА и математичка неисправност Лоренцове трансформације у специјалној теорији релативности Александар Вукеља www.
 ТРОУГАО БРЗИНА и математичка неисправност Лоренцове трансформације у специјалној теорији релативности Александар Вукеља aleksandar@masstheory.org www.masstheory.org Август 2007 О ауторским правима: Дело
ТРОУГАО БРЗИНА и математичка неисправност Лоренцове трансформације у специјалној теорији релативности Александар Вукеља aleksandar@masstheory.org www.masstheory.org Август 2007 О ауторским правима: Дело
PowerPoint Presentation
 РЕДЕФИНИЦИЈА АМПЕРА Агенда међународне активности 2017-2019 o 20. 10. 2017. - 106. састанак CIPM - усвојена резолуција која препоручује редефиниције основних мерних јединица SI (килограма, ампера, келвина
РЕДЕФИНИЦИЈА АМПЕРА Агенда међународне активности 2017-2019 o 20. 10. 2017. - 106. састанак CIPM - усвојена резолуција која препоручује редефиниције основних мерних јединица SI (килограма, ампера, келвина
Р273 Пројектовање база података Примери питања за колоквијум 1. Навести најважније моделе података кроз историју рачунарства до данас. 2. Објаснити ос
 Р273 Пројектовање база података Примери питања за колоквијум 1. Навести најважније моделе података кроз историју рачунарства до данас. 2. Објаснити основне концепте мрежног модела 3. Објаснити основне
Р273 Пројектовање база података Примери питања за колоквијум 1. Навести најважније моделе података кроз историју рачунарства до данас. 2. Објаснити основне концепте мрежног модела 3. Објаснити основне
ТЕОРИЈА УЗОРАКА 2
 ТЕОРИЈА УЗОРАКА 2 12. 04. 13. ВЕЖБАЊА Написати функције за бирање елемената популације обима N у узорак обима n, код простог случајног узорка, користећи алгоритме: Draw by draw procedure for SRS/SRSWOR
ТЕОРИЈА УЗОРАКА 2 12. 04. 13. ВЕЖБАЊА Написати функције за бирање елемената популације обима N у узорак обима n, код простог случајног узорка, користећи алгоритме: Draw by draw procedure for SRS/SRSWOR
ASAS AS ASAS
 Распоред наставе за предмете Мастер академских студија 2017/18. M14014 Big data у електронском пословању 19.фебруар 2018. 21.фебруар 2018. 23.фебруар 2018. М14998 Cloud инфраструктуре и сервиси М09293
Распоред наставе за предмете Мастер академских студија 2017/18. M14014 Big data у електронском пословању 19.фебруар 2018. 21.фебруар 2018. 23.фебруар 2018. М14998 Cloud инфраструктуре и сервиси М09293
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аут
 Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Иван Жупунски, Небојша Пјевалица, Марјан Урекар,
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Иван Жупунски, Небојша Пјевалица, Марјан Урекар,
ПА-4 Машинско учење-алгоритми машинског учења
 ПА-4 Машинско учење-алгоритми машинског учења Машинско учење увод и основни појмови Деф: the desgn and development of algorthms that allow computers to mprove ther performance over tme based on data sensor
ПА-4 Машинско учење-алгоритми машинског учења Машинско учење увод и основни појмови Деф: the desgn and development of algorthms that allow computers to mprove ther performance over tme based on data sensor
Microsoft PowerPoint - MODELOVANJE-predavanje 9.ppt [Compatibility Mode]
![Microsoft PowerPoint - MODELOVANJE-predavanje 9.ppt [Compatibility Mode] Microsoft PowerPoint - MODELOVANJE-predavanje 9.ppt [Compatibility Mode]](/thumbs/104/162378327.jpg) MODELONJE I SIMULIJ PROES 9. Rešavanje dinamičkih modela; osnovni pojmovi upravljanja procesima http://elektron.tmf.bg.ac.rs/mod Dr Nikola Nikačević METODE Z REŠNJE LINERNIH DINMIČKIH MODEL 1. remenski
MODELONJE I SIMULIJ PROES 9. Rešavanje dinamičkih modela; osnovni pojmovi upravljanja procesima http://elektron.tmf.bg.ac.rs/mod Dr Nikola Nikačević METODE Z REŠNJE LINERNIH DINMIČKIH MODEL 1. remenski
GODIŠNJI KALENDAR ISPITA Inženjerski menadžment (OSNOVNE AKADEMSKE STUDIJE) ŠKOLSKA 2018/2019. GODINA Rbr
 GODIŠNJI KALENDAR ISPITA Inženjerski menadžment (OSNOVNE AKADEMSKE STUDIJE) ŠKOLSKA 2018/2019. GODINA Rbr 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Predmet Godina Januarski rok Februarski
GODIŠNJI KALENDAR ISPITA Inženjerski menadžment (OSNOVNE AKADEMSKE STUDIJE) ŠKOLSKA 2018/2019. GODINA Rbr 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Predmet Godina Januarski rok Februarski
Paper Title (use style: paper title)
 Статистичка анализа коришћења електричне енергије која за последицу има примену повољнијег тарифног става Аутор: Марко Пантовић Факултет техничких наука, Чачак ИАС Техника и информатика, 08/09 e-mal адреса:
Статистичка анализа коришћења електричне енергије која за последицу има примену повољнијег тарифног става Аутор: Марко Пантовић Факултет техничких наука, Чачак ИАС Техника и информатика, 08/09 e-mal адреса:
PowerPoint Presentation
 Показатељи технолошког напретка Технолошки развој Резултира стварањем нових или побољшањем постојећих производа, процеса и услуга. Технолошки развој - део економског и друштвеног развоја. Научни и технолошки
Показатељи технолошког напретка Технолошки развој Резултира стварањем нових или побољшањем постојећих производа, процеса и услуга. Технолошки развој - део економског и друштвеног развоја. Научни и технолошки
Model podataka
 Fakultet organizacionih nauka Uvod u informacione sisteme Doc. Dr Ognjen Pantelić Modeliranje podataka definisanje strategije snimanje postojećeg stanja projektovanje aplikativno modeliranje implementacija
Fakultet organizacionih nauka Uvod u informacione sisteme Doc. Dr Ognjen Pantelić Modeliranje podataka definisanje strategije snimanje postojećeg stanja projektovanje aplikativno modeliranje implementacija
( )
 Заштита животне средине Основе механике (кратак преглед предмета) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj 1. Информациjе о предмету
Заштита животне средине Основе механике (кратак преглед предмета) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj 1. Информациjе о предмету
Slide 1
 ИНФОРМАЦИЈА КОМУНИКОЛОГИЈА 8. ТЕМА САДРЖАЈ ПРЕДАВАЊА Појам информације Религиозно и метанаучно одређења информације Кибернетски приступ информацији Социоантрополошко схватање информације ПОЈАМ ИНФОРМАЦИЈЕ
ИНФОРМАЦИЈА КОМУНИКОЛОГИЈА 8. ТЕМА САДРЖАЈ ПРЕДАВАЊА Појам информације Религиозно и метанаучно одређења информације Кибернетски приступ информацији Социоантрополошко схватање информације ПОЈАМ ИНФОРМАЦИЈЕ
Na osnovu člana 33 stav 9 Zakona o zaštiti od nejonizujućih zračenja ( Službeni list CG, broj 35/13) Ministarstvo održivog razvoja i turizma, donijelo
 Na osnovu člana 33 stav 9 Zakona o zaštiti od nejonizujućih zračenja ( Službeni list CG, broj 35/13) Ministarstvo održivog razvoja i turizma, donijelo je PRAVILNIK O BLIŽEM SADRŽAJU AKCIONOG PROGRAMA O
Na osnovu člana 33 stav 9 Zakona o zaštiti od nejonizujućih zračenja ( Službeni list CG, broj 35/13) Ministarstvo održivog razvoja i turizma, donijelo je PRAVILNIK O BLIŽEM SADRŽAJU AKCIONOG PROGRAMA O
Зборник радова 6. Међународне конференције о настави физике у средњим школама, Алексинац, март Одређивање коефицијента пригушења у ваздуху
 Одређивање коефицијента пригушења у ваздуху помоћу линеарног хармонијског осцилатора Соња Ковачевић 1, Милан С. Ковачевић 2 1 Прва крагујевачка гимназија, Крагујевац, Србија 2 Природно-математички факултет,
Одређивање коефицијента пригушења у ваздуху помоћу линеарног хармонијског осцилатора Соња Ковачевић 1, Милан С. Ковачевић 2 1 Прва крагујевачка гимназија, Крагујевац, Србија 2 Природно-математички факултет,
ASAS AS ASAS
 Распоред испита за предмете Мастер академских студија Испитни рок: Maj 2019. Шифра Предмет Студијски програм Датум Време Сала Број пријављених / Напомена м14014 Big data у електронском пословању сви 13.
Распоред испита за предмете Мастер академских студија Испитни рок: Maj 2019. Шифра Предмет Студијски програм Датум Време Сала Број пријављених / Напомена м14014 Big data у електронском пословању сви 13.
Microsoft Word - HIPOTEZA PROSTORA I VREMENA
 INTERDISCIPLINARNOST SA MEHANIZMOM EVOLUCIJE I HIPOTEZOM PROSTORA I VREMENA Dvadeset i prvi vek će, u prvom redu, biti vek interdisciplinarnosti. Nacionalna akademija nauka SAD Fizika se ograničava na
INTERDISCIPLINARNOST SA MEHANIZMOM EVOLUCIJE I HIPOTEZOM PROSTORA I VREMENA Dvadeset i prvi vek će, u prvom redu, biti vek interdisciplinarnosti. Nacionalna akademija nauka SAD Fizika se ograničava na
ASAS AS ASAS
 Распоред испита за предмете Мастер академских студија Испитни рок: Април 2019. Шифра Предмет Студијски програм Датум Време Сала Број пријављених / Напомена м14014 Big data у електронском пословању сви
Распоред испита за предмете Мастер академских студија Испитни рок: Април 2019. Шифра Предмет Студијски програм Датум Време Сала Број пријављених / Напомена м14014 Big data у електронском пословању сви
Microsoft Word - ROKI doc
 UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU Žarko M. Janković ODRŽAVANJE TEHNIČKIH SISTEMA Niš, 2017. ODRŽAVANJE TEHNIČKIH SISTEMA Autor Dr Žarko M. Janković, red. prof. Fakultet zaštite na radu
UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU Žarko M. Janković ODRŽAVANJE TEHNIČKIH SISTEMA Niš, 2017. ODRŽAVANJE TEHNIČKIH SISTEMA Autor Dr Žarko M. Janković, red. prof. Fakultet zaštite na radu
Microsoft PowerPoint - jkoren10.ppt
 Dickey-Fuller-ov test jediničnog korena Osnovna ideja Različite determinističke komponente Izračunavanje test-statistike Pravilo odlučivanja Određivanje broja jediničnih korena Algoritam testiranja Prošireni
Dickey-Fuller-ov test jediničnog korena Osnovna ideja Različite determinističke komponente Izračunavanje test-statistike Pravilo odlučivanja Određivanje broja jediničnih korena Algoritam testiranja Prošireni
Школа Ј. Ј. Змај Свилајнац МЕСЕЧНИ ПЛАН РАДА ЗА СЕПТЕМБАР Школска 2018 /2019. Назив предмета: Информатика и рачунарство Разред: 5. Недељни број часова
 Школа Ј. Ј. Змај Свилајнац МЕСЕЧНИ ПЛАН РАДА ЗА СЕПТЕМБАР јединице 1. 1. Увод у информатику и рачунарство 1. 2. Oрганизација података на рачунару 1. 3. Рад са текстуалним документима 1. 4. Форматирање
Школа Ј. Ј. Змај Свилајнац МЕСЕЧНИ ПЛАН РАДА ЗА СЕПТЕМБАР јединице 1. 1. Увод у информатику и рачунарство 1. 2. Oрганизација података на рачунару 1. 3. Рад са текстуалним документима 1. 4. Форматирање
P11.3 Analiza zivotnog veka, Graf smetnji
 Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
Uvod u statistiku
 Uvod u statistiku Osnovni pojmovi Statistika nauka o podacima Uključuje prikupljanje, klasifikaciju, prikaz, obradu i interpretaciju podataka Staistička jedinica objekat kome se mjeri neko svojstvo. Svi
Uvod u statistiku Osnovni pojmovi Statistika nauka o podacima Uključuje prikupljanje, klasifikaciju, prikaz, obradu i interpretaciju podataka Staistička jedinica objekat kome se mjeri neko svojstvo. Svi
Elementarna matematika 1 - Oblici matematickog mišljenja
 Oblici matematičkog mišljenja 2007/2008 Mišljenje (psihološka definicija) = izdvajanje u čovjekovoj spoznaji odre denih strana i svojstava promatranog objekta i njihovo dovo denje u odgovarajuće veze s
Oblici matematičkog mišljenja 2007/2008 Mišljenje (psihološka definicija) = izdvajanje u čovjekovoj spoznaji odre denih strana i svojstava promatranog objekta i njihovo dovo denje u odgovarajuće veze s
Microsoft PowerPoint - Ispitivanje povezanosti Regresija redovni decembar 2007 [Compatibility Mode]
![Microsoft PowerPoint - Ispitivanje povezanosti Regresija redovni decembar 2007 [Compatibility Mode] Microsoft PowerPoint - Ispitivanje povezanosti Regresija redovni decembar 2007 [Compatibility Mode]](/thumbs/100/145919354.jpg) Ispitivanje povezanosti Jelena Marinkovi Institut za medicinsku statistiku i informatiku Medicinskog fakulteta Beograd, decembar 2007.g. Kakav je odnos DOZA-EFEKAT (ODGOVOR)? Log Doza vs Odgovor 150 y-osa
Ispitivanje povezanosti Jelena Marinkovi Institut za medicinsku statistiku i informatiku Medicinskog fakulteta Beograd, decembar 2007.g. Kakav je odnos DOZA-EFEKAT (ODGOVOR)? Log Doza vs Odgovor 150 y-osa
Slide 1
 Анализа електроенергетских система -Прорачун кратких спојева- Кратак спој представља поремећено стање мреже, односно поремећено стање система. За време трајања кратког споја напони и струје се мењају са
Анализа електроенергетских система -Прорачун кратких спојева- Кратак спој представља поремећено стање мреже, односно поремећено стање система. За време трајања кратког споја напони и струје се мењају са
KATALOG ZNANJA IZ INFORMATIKE
 KATALOG ZNANJA IZ INFORMATIKE Nacionalni savjet za obrazovanje je na 27. sjednici održanoj 17. marta 2014. godine utvrdio izmjene predmetnoga programa INFORMATIKA za I razred gimnazije. Na zahtijev Pedagoško-psihološke
KATALOG ZNANJA IZ INFORMATIKE Nacionalni savjet za obrazovanje je na 27. sjednici održanoj 17. marta 2014. godine utvrdio izmjene predmetnoga programa INFORMATIKA za I razred gimnazije. Na zahtijev Pedagoško-psihološke
Microsoft Word - Predmet 14-Strategijski menadzment-rjesenja
 КОМИСИЈА ЗА РАЧУНОВОДСТВО И РЕВИЗИЈУ БОСНЕ И ХЕРЦЕГОВИНЕ ИСПИТ ЗА СТИЦАЊЕ ПРОФЕСИОНАЛНОГ ЗВАЊА ОВЛАШТЕНИ РЕВИЗОР (ИСПИТНИ ТЕРМИН: МАЈ 2016. ГОДИНЕ) ПРЕДМЕТ 14: СТРАТЕГИЈСКИ МЕНАЏМЕНТ ЕСЕЈИ Есеј број 1
КОМИСИЈА ЗА РАЧУНОВОДСТВО И РЕВИЗИЈУ БОСНЕ И ХЕРЦЕГОВИНЕ ИСПИТ ЗА СТИЦАЊЕ ПРОФЕСИОНАЛНОГ ЗВАЊА ОВЛАШТЕНИ РЕВИЗОР (ИСПИТНИ ТЕРМИН: МАЈ 2016. ГОДИНЕ) ПРЕДМЕТ 14: СТРАТЕГИЈСКИ МЕНАЏМЕНТ ЕСЕЈИ Есеј број 1
На основу члана 15. и члана 59. став 2. Закона о Агенцији за борбу против корупције ( Службени гласник РС, бр. 97/08, 53/10, 66/11 - одлука УС, 67/13
 На основу члана 15. и члана 59. став 2. Закона о Агенцији за борбу против корупције ( Службени гласник РС, бр. 97/08, 53/10, 66/11 - одлука УС, 67/13 - одлука УС, 112/13 - аутентично тумачење и 8/15 -
На основу члана 15. и члана 59. став 2. Закона о Агенцији за борбу против корупције ( Службени гласник РС, бр. 97/08, 53/10, 66/11 - одлука УС, 67/13 - одлука УС, 112/13 - аутентично тумачење и 8/15 -
УНИВЕРЗИТЕТ У ИСТОЧНОМ САРАЈЕВУ МАШИНСКИ ФАКУЛТЕТ ИСТОЧНО САРАЈЕВО ИСПИТНИ ТЕРМИНИ ЗА ШКОЛСКУ 2018./2019. НАПОМЕНА: Испите обавезно пријавити! ПРЕДМЕТ
 УНИВЕРЗИТЕТ У ИСТОЧНОМ САРАЈЕВУ МАШИНСКИ ФАКУЛТЕТ ИСТОЧНО САРАЈЕВО ИСПИТНИ ЗА ШКОЛСКУ 2018./2019. I ГОДИНА II 1 МАТЕМАТИКА 1 07.02. 21.02. 18.04. 400 20.06. 04.07. 0.09. 19.09. 400 2 МЕХАНИКА 1 08.02.
УНИВЕРЗИТЕТ У ИСТОЧНОМ САРАЈЕВУ МАШИНСКИ ФАКУЛТЕТ ИСТОЧНО САРАЈЕВО ИСПИТНИ ЗА ШКОЛСКУ 2018./2019. I ГОДИНА II 1 МАТЕМАТИКА 1 07.02. 21.02. 18.04. 400 20.06. 04.07. 0.09. 19.09. 400 2 МЕХАНИКА 1 08.02.
POSLOVNI INFORMACIONI SISTEMI I RA^UNARSKE
 ZNAČAJ RAČUNARSKIH KOMUNIKACIJA U BANKARSKOM POSLOVANJU RAČUNARSKE MREŽE Računarske mreže su nastale kombinacijom računara i telekomunikacija dve tehnologije sa veoma različitom tradicijom i istorijom.
ZNAČAJ RAČUNARSKIH KOMUNIKACIJA U BANKARSKOM POSLOVANJU RAČUNARSKE MREŽE Računarske mreže su nastale kombinacijom računara i telekomunikacija dve tehnologije sa veoma različitom tradicijom i istorijom.
QFD METODA – PRIMER
 QFD METODA - PRIMER PROBLEM: U kompaniji X koja se bavi izradom kompjuterskih softvera uočen je pad prodaje konkretnog softvera - Softver za vođenje knjigovodstva. Kompanija X je raspolagala sa jednom
QFD METODA - PRIMER PROBLEM: U kompaniji X koja se bavi izradom kompjuterskih softvera uočen je pad prodaje konkretnog softvera - Softver za vođenje knjigovodstva. Kompanija X je raspolagala sa jednom
Tehničko rešenje: Industrijski prototip dvostrukog trofaznog analizatora snage sa funkcijama merenja kvaliteta električne energije tipska oznaka MM2 R
 Tehničko rešenje: Industrijski prototip dvostrukog trofaznog analizatora snage sa funkcijama merenja kvaliteta električne energije tipska oznaka MM2 Rukovodilac projekta: Vladimir Vujičić Odgovorno lice:
Tehničko rešenje: Industrijski prototip dvostrukog trofaznog analizatora snage sa funkcijama merenja kvaliteta električne energije tipska oznaka MM2 Rukovodilac projekta: Vladimir Vujičić Odgovorno lice:
Microsoft Word - finansijski administrator_zasnovanost kvalifikacije.doc
 ОБРАЗОВНИ ПРОФИЛ ФИНАНСИЈСКИ АДМИНИСТРАТОР СТАНДАРД КВАЛИФИКАЦИЈЕ, ЦИЉЕВИ И ИСХОДИ СТРУЧНОГ ОБРАЗОВАЊА 1. Назив квалификације: Финансијски администратор 2. Подручје рада: Економија, право и администрација
ОБРАЗОВНИ ПРОФИЛ ФИНАНСИЈСКИ АДМИНИСТРАТОР СТАНДАРД КВАЛИФИКАЦИЈЕ, ЦИЉЕВИ И ИСХОДИ СТРУЧНОГ ОБРАЗОВАЊА 1. Назив квалификације: Финансијски администратор 2. Подручје рада: Економија, право и администрација
Microsoft PowerPoint - Pokazatelji TP i stopa TP_ za studente [Compatibility Mode]
![Microsoft PowerPoint - Pokazatelji TP i stopa TP_ za studente [Compatibility Mode] Microsoft PowerPoint - Pokazatelji TP i stopa TP_ za studente [Compatibility Mode]](/thumbs/100/146045939.jpg) Показатељи технолошког напретка Технолошки развој Резултира стварањем новихили побољшањем постојећихпроизвода, процеса и услуга. Технолошки развој - део економског и друштвеног развоја. Научни и технолошки
Показатељи технолошког напретка Технолошки развој Резултира стварањем новихили побољшањем постојећихпроизвода, процеса и услуга. Технолошки развој - део економског и друштвеног развоја. Научни и технолошки
Mere slicnosti
 Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
Softversko inženjerstvo
 Softversko inženjerstvo OAS SOFTVERSKO INŽENJERSTBO Trajanje studija: 4 godine Broj ESPB: 240 ESPB Izborni moduli: Modul SI: Softversko inženjerstvo Modul RI: Razvoj igara Modul SI: Softversko inženjerstvo
Softversko inženjerstvo OAS SOFTVERSKO INŽENJERSTBO Trajanje studija: 4 godine Broj ESPB: 240 ESPB Izborni moduli: Modul SI: Softversko inženjerstvo Modul RI: Razvoj igara Modul SI: Softversko inženjerstvo
PowerPoint Presentation
 Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
DUBINSKA ANALIZA PODATAKA
 DUBINSKA ANALIZA PODATAKA () ASOCIJACIJSKA PRAVILA (ENGL. ASSOCIATION RULE) Studeni 2018. Mario Somek SADRŽAJ Asocijacijska pravila? Oblici učenja pravila Podaci za analizu Algoritam Primjer Izvođenje
DUBINSKA ANALIZA PODATAKA () ASOCIJACIJSKA PRAVILA (ENGL. ASSOCIATION RULE) Studeni 2018. Mario Somek SADRŽAJ Asocijacijska pravila? Oblici učenja pravila Podaci za analizu Algoritam Primjer Izvođenje
Jezička politika, jezičko planiranje i standardizacija jezika.
 Jezička politika, jezičko planiranje i standardizacija jezika PhDs Ljatif Demir Univerzitet Zagreb Jezička politika kao definicija Tipično sociolingvistički pojam jezička politika u lingvistickoj literaturi
Jezička politika, jezičko planiranje i standardizacija jezika PhDs Ljatif Demir Univerzitet Zagreb Jezička politika kao definicija Tipično sociolingvistički pojam jezička politika u lingvistickoj literaturi
untitled
 С А Д Р Ж А Ј Предговор...1 I II ОСНОВНИ ПОЈМОВИ И ДЕФИНИЦИЈЕ...3 1. Предмет и метод термодинамике... 3 2. Термодинамички систем... 4 3. Величине (параметри) стања... 6 3.1. Специфична запремина и густина...
С А Д Р Ж А Ј Предговор...1 I II ОСНОВНИ ПОЈМОВИ И ДЕФИНИЦИЈЕ...3 1. Предмет и метод термодинамике... 3 2. Термодинамички систем... 4 3. Величине (параметри) стања... 6 3.1. Специфична запремина и густина...
PLAN I PROGRAM ZA DOPUNSKU (PRODUŽNU) NASTAVU IZ MATEMATIKE (za 1. razred)
 PLAN I PROGRAM ZA DOPUNSKU (PRODUŽNU) NASTAVU IZ MATEMATIKE (za 1. razred) Učenik prvog razreda treba ostvarit sljedeće minimalne standarde 1. SKUP REALNIH BROJEVA -razlikovati brojevne skupove i njihove
PLAN I PROGRAM ZA DOPUNSKU (PRODUŽNU) NASTAVU IZ MATEMATIKE (za 1. razred) Učenik prvog razreda treba ostvarit sljedeće minimalne standarde 1. SKUP REALNIH BROJEVA -razlikovati brojevne skupove i njihove
______________________ sudu u ___________________
 На основу члана 14. став 1. Закона о безбедности и здрављу на раду (даље: Закон), Школски одбор наседници одржаној дана 30.03.2018. години доноси ПРАВИЛНИК О БЕЗБЕДНОСТИ И ЗДРАВЉУ НА РАДУ ТЕХНИЧКЕ ШКОЛЕ
На основу члана 14. став 1. Закона о безбедности и здрављу на раду (даље: Закон), Школски одбор наседници одржаној дана 30.03.2018. години доноси ПРАВИЛНИК О БЕЗБЕДНОСТИ И ЗДРАВЉУ НА РАДУ ТЕХНИЧКЕ ШКОЛЕ
ФАКУЛТЕТ ОРГАНИЗАЦИОНИХ НАУКА
 Питања за усмени део испита из Математике 3 I. ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ 1. Појам диференцијалне једначине. Пикарова теорема. - Написати општи и нормални облик диференцијалне једначине првог реда. - Дефинисати:
Питања за усмени део испита из Математике 3 I. ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ 1. Појам диференцијалне једначине. Пикарова теорема. - Написати општи и нормални облик диференцијалне једначине првог реда. - Дефинисати:
Matematka 1 Zadaci za vežbe Oktobar Uvod 1.1. Izračunati vrednost izraza (bez upotrebe pomoćnih sredstava): ( ) [ a) : b) 3 3
 Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
Microsoft PowerPoint - GR_MbIS_12_IDEF
 Menadžment poslovnih informacionih sistema - 12 metode modeliranja funkcija pripremila Doc. dr Gordana Radić Integfated DEFinition Definicija: je metoda (jezik) modeliranja bazirana je na kombinaciji grafike
Menadžment poslovnih informacionih sistema - 12 metode modeliranja funkcija pripremila Doc. dr Gordana Radić Integfated DEFinition Definicija: je metoda (jezik) modeliranja bazirana je na kombinaciji grafike
Osnovni pojmovi teorije verovatnoce
 Osnovni pojmovi teorije verovatnoće Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2019 Milan Merkle Osnovni pojmovi ETF Beograd 1 / 13 Verovatnoća i statistika:
Osnovni pojmovi teorije verovatnoće Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2019 Milan Merkle Osnovni pojmovi ETF Beograd 1 / 13 Verovatnoća i statistika:
Рачунарска интелигенција
 Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Praćenje kvaliteta zdravstvene zaštite u Republici Srbiji Nada Kosić Bibić 1, Snežana Pinter 1 1 Zavod za javno zdravlje Subotica Sažetak: Opredeljenj
 Praćenje kvaliteta zdravstvene zaštite u Republici Srbiji Nada Kosić Bibić 1, Snežana Pinter 1 1 Zavod za javno zdravlje Subotica Sažetak: Opredeljenje za organizovani, sistemski pristup stalnom unapređenju
Praćenje kvaliteta zdravstvene zaštite u Republici Srbiji Nada Kosić Bibić 1, Snežana Pinter 1 1 Zavod za javno zdravlje Subotica Sažetak: Opredeljenje za organizovani, sistemski pristup stalnom unapređenju
Задатак 4: Центрифугална пумпа познате карактеристике при n = 2900 min -1 ради на инсталацији приказаној на слици и потискује воду из резервоара А у р
 Задатак 4: Центрифугална пумпа познате карактеристике при n = 900 min -1 ради на инсталацији приказаној на слици и потискује воду из резервоара А у резервоар B. Непосредно на излазу из пумпе постављен
Задатак 4: Центрифугална пумпа познате карактеристике при n = 900 min -1 ради на инсталацији приказаној на слици и потискује воду из резервоара А у резервоар B. Непосредно на излазу из пумпе постављен
Projektovanje informacionih sistema i baze podataka
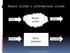 Realni sistem i informacioni sistem Ulaz Realni sistem Izlaz Unos Baza podataka Izveštaji Realni sistem i informacioni sistem Sistem se definiše kao skup objekata (entiteta) i njihovih međusobnih veza
Realni sistem i informacioni sistem Ulaz Realni sistem Izlaz Unos Baza podataka Izveštaji Realni sistem i informacioni sistem Sistem se definiše kao skup objekata (entiteta) i njihovih međusobnih veza
