PowerPoint Presentation
|
|
|
- Светолик Радојчић
- пре 6 година
- Прикази:
Транскрипт
1 Једнократна промена сале за предавања! О Б А В Е Ш Т Е Њ Е У петак, 26. октобра године, предавања из предмета Инжењерски оптимизациони алгоритми 13С074ИОА у термину од , одржаће се у амфитеатру 56. Инжењерски оптимизациони алгоритми 1/30
2 NFL теорема NO-FREE-LUNCH theorem Wolpert, D.H.; Macready, W.G., "No free lunch theorems for optimization," Evolutionary Computation, IEEE Transactions on, vol.1, no.1, pp , Apr 1997 уколико су све оптимизационе функције једнако вероватне, сви опт. алгоритми су једнако (не)ефикасни Зашто бисмо онда разматрали различите оптимизационе алгоритме? Инжењерски оптимизациони алгоритми 2/30
3 Пример функције уз NFL теорему f ( x) 0, ln(1 10x), P i 1,2,... N, rand x x P i Пример мало вероватне оптимизационе функције Овакав проблем није инжењерски добро дефинисан Инжењерски оптимизациони алгоритми 3/30
4 Критички осврт на NFL теорему (познати докази када НЕ важи) D.W. Corne, J.D. Knowles, Some multiobjective optimizers are better than the others, Proc. of IEEE CEC 2003, pp For multiobjective optimization, NFL does not hold C. Igel, M. Toussaint, A No-Free-Lunch theorem for nonuniform distributions of target functions, J. Math. Model. Algorithms 3(4), pp (2004) Classes of functions relevant in practice are not likely to satisfy the NFL scenario A. Auger, O. Teytaud, Continuous lunches are free plus the design of optimal optimization algorithms, Algorithmica 57, 2010, pp For continuous domains, NFL does not hold Инжењерски оптимизациони алгоритми 4/30
5 Пример инжењерског проблема: минимизација слабљења кабла Коаксијални кабл полупречници a и b површинска отпорност R s задато b (габарит) Пронаћи b/a тако да је α p минимално Непрекидна и диференцијабилна опт. функција Постоји јасна узрочно-последична зависност побуде (b/a) и одзива (α p ) p a Rs a b 60 b 2 ln a r b 240 b Инжењерски оптимизациони алгоритми 5/30 R s r b a ln 1 b a
6 Инжењерска пракса: неки алгоритми су БОЉИ Пракса: оптимизациона функција је смислено формулисана оптимизациони проблем је једнозначан поновљивост везе улаз-излаз црне кутије Инжењерски проблем подразумева узрочно-последичну везу неке оптимизационе функције су много вероватније од других У инжењерској пракси: неки оптимизациони алгоритми су знатно бољи од других алгоритама Инжењерски оптимизациони алгоритми 6/30
7 Комплексност алгоритма и поређење перформанси алгоритама Претпоставимо да алгоритам обрађује N улазних елемената Рачунска комплексност алгоритма линеарна, квадратна, логаритамска, итд. Означавање O(N), O(N 2 ), O(logN), итд. Генерално: алгоритми се пореде према комплексности (која је пропорционална времену потребном за извршавање алгоритма) За оптимизационе алгоритме, тражићемо и најбрже проналажње (средњег) најбољег решења Инжењерски оптимизациони алгоритми 7/30
8 Случајно претраживање На случајан начин генеришу се тачке у којима се рачуна функција грешке Најчешће се користи генератор са униформном расподелом Неефикасан начин оптимизације јер су претходно и наредно израчунавање оптимизационе функције независни (иста тачка може да се испита више пута) Добар начин за грубу претрагу простора Сложеност O(N), N број одбирака оптимизационог простора Инжењерски оптимизациони алгоритми 8/30
9 Генератори случајних бројева Рачунарско генерисање случајних бројева је нетривијалан задатак Генератори који постоје у библиотекама пролазе строге тестове случајности само делимично! Доступне функције: C/C++: rand(), srand(), boost/random MATLAB: rand(), randn(), randi() Python: random.randint, random.uniform Инжењерски оптимизациони алгоритми 9/30
10 Једноставна рутина за генерисање целих случајних бројева Опсег а ξ b Ограничење: RAND_MAX Ограничење зависи од компајлера (VS2017 RAND_MAX = 32768) Уколико је потребaн већи опсег генерисати произвољан низ бита {0,1} и претворити га у цео број генерисати два или више цела броја и њихове бите интерпретирати као бите већег целог броја Инжењерски оптимизациони алгоритми 10/30
11 Једноставнa рутина за генерисање реалних случајних бројева Опсег а ξ b Грануларност 1/RAND_MAX Уколико је потребна већа грануларност: Опсег [a, b] поделити на више подопсега и сабрати (случајне) бројеве из подопсега Инжењерски оптимизациони алгоритми 11/30
12 C++11 <random> Инжењерски оптимизациони алгоритми 12/30
13 Пример: различита решења при сваком покретању #1 #2 #3 #4 Инжењерски оптимизациони алгоритми 13/30
14 Пример случајног претраживања једне 2D функције Инжењерски оптимизациони алгоритми 14/30
15 О случајним процесима... (by Piet Hein) Whenever you're called on to make up your mind, and you're hampered by not having any, the best way to solve the dilemma, you'll find, is simply by spinning a penny. No - not so that chance shall decide the affair while you're passively standing there moping; but the moment the penny is up in the air, you suddenly know what you're hoping. Инжењерски оптимизациони алгоритми 15/30
16 Систематско претраживање: континуалне променљиве За сваки оптимизациони параметар задаје се број корака (или дужина) Вишедимензионална мрежа се формира у оптимизационом простору У сваком чвору мреже израчунава се оптимизациона функција За D-димензионални оптимизациони простор укупан број итерација је k 1 * k 2 * *k D, где је k i број корака по димензији i Сложеност алгоритма је O(N D ), N број корака по једној димензији D број димензија оптимизационог простора Инжењерски оптимизациони алгоритми 16/30
17 Систематско претраживање једне континуалне функције Инжењерски оптимизациони алгоритми 17/30
18 Систематско претраживање: дискретне променљиве Проверити СВА дискретна стања у оптимизационом простору Примери: испитати сва дискретна стања прекидача испитати све варијације са понављањем испитати све комбинације без понављања испитати све пермутације без понављања... Истинитосне таблице при испитивању таутологије у логици Инжењерски оптимизациони алгоритми 18/30
19 Варијације са понављањем (Систематско претраживање SAT) На колико начина се може распоредити n елемената на k места? Број начина распоређивања је n k Формирање као број са k цифара, а цифре су 1...n: 1111, 1112, 111n 1121, 1122, 112n... nnn1, nnn2, nnnn Инжењерски оптимизациони алгоритми 19/30
20 Комбинације без понављања Подскуп од k елемента бирамо из скупа од n елемената Број n n! избора је k ( n k)! k! Логика: Поставити k елемената на прва слободна места сa левe стране Померити крајњи десни удесно, за по једно место, док може Померити први слободни са десне стране за једно место, а остале десно од њега ставити до њега Поновити, док сви не буду десно Инжењерски оптимизациони алгоритми 20/30
21 Пермутације без понављања (Систематско претраживање TSP) На колико начина је могуће распоредити n елемената на n места? Број различитих распореда је n! Алгоритам изабран по критеријуму минималног броја линија кода Колико највише пермутација може да се изврши за 1 min? Колико је времена потребно за N=20? ** C/C++ #include <algorithm> std::next_permutation( ) Инжењерски оптимизациони алгоритми 21/30
22 Како алгоритам ради? Стања алгоритма за 3 елемента k= 2 i= 3 P={ 1 2 3} P={ 1 2 0} k= 2 i= 2 P={ 1 3 2} P={ 1 0 2} k= 2 i= 3 P={ 2 1 3} P={ 2 1 0} k= 2 i= 1 P={ 3 1 2} P={ 2} k= 2 i= 2 P={ 2 3 1} P={ 2 } k= 2 i= 1 P={ 3 2 1} P={ 0 2 1} k= 1 i= 2 P={ 1 2 0} k= 1 i= 2 P={ 1 0 0} k= 1 i= 3 P={ 1 0 2} k= 1 i= 3 P={ 1 0 0} k= 1 i= 1 P={ 2 1 0} k= 1 i= 1 P={ 0} k= 1 i= 3 P={ 2} k= 1 i= 3 P={ 0} k= 1 i= 1 P={ 2 } k= 1 i= 1 P={ 0 } k= 1 i= 2 P={ 0 2 1} k= 1 i= 2 P={ 0 } k= 0 i= 1 P={ 1 0 0} k= 0 i= 1 P={ 0 0 0} k= 0 i= 2 P={ 0} k= 0 i= 2 P={ 0 0 0} k= 0 i= 3 P={ 0 } k= 0 i= 3 P={ 0 0 0} k= -1 i= 1 P={ 0 0 0} k= -1 i= 1 P={ 0 0 0} Инжењерски оптимизациони алгоритми 22/30
23 Систематско претраживање: особине и употреба Уколико желимо да докажемо да смо нашли глобални оптимум (најбоље могуће решење) једини начин је да систематски претражимо читав оптимизациони простор, у општем случају За разлику од случајног претраживања једно решење се једном и само једном проверава Континуалне променљиве: систематско претраживање подразумева коначан корак за сваку димензију (тачност) решење смо нашли са тачношћу која је пропорционална кораку Дискретне променљиве: сва решења су проверена Инжењерски оптимизациони алгоритми 23/30
24 Варијације: хијерархијско систематско претраживање Проценити део простора и претражити га са мањим кораком у наредном нивоу 1. ниво 2. ниво 3. ниво Инжењерски оптимизациони алгоритми 24/30
25 Варијације: гранање и одсецање (branch & cut, backtracking) Минимизирати дискретну функцију: f ( b b k 3, b 2 0,1, b 1, b 0 ) 3 k 0 b k 2 k 0 1 Инжењерски оптимизациони алгоритми 25/30
26 Гранање и одсецање: прескочити део простора f ( 0,1,1,0) Познато f(0,1,1,0) = 6 Претраживање f(1,?,?,?) 8 непотребно 0 Простор смањен 2 пута! f ( 1,0,0,0) Инжењерски оптимизациони алгоритми 26/30
27 Други називи и особине систематског претраживања Други називи за систематско претраживање Grid search Brute-force search Parameter sweep Exhaustive search Generate & test Најбољи могући приступ уколико можемо да сачекамо да се претрага заврши (оптимизациони простор је мали) Уколико претрага траје недопустиво дуго, није од користи (оптмизациони простор је велики) Погодан за извршавање у паралели на рачунарима са више процесора (језгара) Инжењерски оптимизациони алгоритми 27/30
28 Задатак за вежбе #2 (Оптимално бушење плочице) Штампана плочица се израђује аутоматски На њој постоји више рупа истог пречника које је потребно избушити Аутоматска бургија има коначну брзину позиционирања Израђује се велики број идентичних плочица Уштеда времена израде једне плочице је од великог практичног интереса (множи се бројем плочица у серији) Потребно је минимизирати пут који пређе бургија (и минимизирати време израде) Бургија се не враћа на место полазне рупе када заврши један циклус бушења (у пракси, враћа се истом путањом уназад) Координате рупа на слици су дате у милиметрима Инжењерски оптимизациони алгоритми 28/30
29 Координате тачка у [mm] на штампаној плочици 19 (2.7, 56.8) 17 (9.1, 52.8) 16 (15.1, 49.6) 14 (21.5, 45.8) 12 (33.4, 60.5) 3 (51.7, 56.0) 8 (34.7, 45.1) 1 (62.0, 58.4) 2 (57.5, 56.0) 5 (57.7, 42.1) 4 (67.9,19.6) 10 (34.7, 26.4) 11 (28.4, 31.7) 6 (54.2, 29.1) 7 (46.0, 45.1) 9 (45.7, 25.1) 13 (22.9, 32.7) 15 (15.3, 37.8) 18 (9.1, 40.3) 20 (2.7, 33.1) Инжењерски оптимизациони алгоритми 29/30
30 Задатак за вежбе #2 (детаљи и израда) Пронаћи најкраћи пут за (а) првих 8 и (б) првих 12 рупа Задатак се своди на TSP проблем са 8 градова (8!= путања) 12 градова (12!= путања) Растојање између два града је L 2 норма (Еуклидовско растојање) Бургија може да крене из било које рупе (од првих 8 (a) или 12 (б)) У код за формирање свих пермутација додати рачунање дужине путање, поређење са претходно нађеном најкраћом путањом и памћење (испис) најкраће пронађене путање Измерити или проценити време извршавања програма * [5] БОНУС: пронаћи (нај)краћи пут за свих 20 рупа ** Lin-Kernighan heuristics [LKH] је једнa од најбољих хеуристика за TSP Инжењерски оптимизациони алгоритми 30/30
PowerPoint Presentation
 Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odr
 Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odrediti njene krajeve. b) Odrediti sledeće skupove: -
Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odrediti njene krajeve. b) Odrediti sledeće skupove: -
06 Poverljivost simetricnih algoritama1
 ЗАШТИТА ПОДАТАКА Симетрични алгоритми заштите поверљивост симетричних алгоритама Преглед биће објашњено: коришћење симетричних алгоритама заштите како би се заштитила поверљивост потреба за добрим системом
ЗАШТИТА ПОДАТАКА Симетрични алгоритми заштите поверљивост симетричних алгоритама Преглед биће објашњено: коришћење симетричних алгоритама заштите како би се заштитила поверљивост потреба за добрим системом
Slide 1
 Statistička analiza u hidrologiji Uvod Statistička analiza se primenjuje na podatke osmatranja hidroloških veličina (najčešće: protoka i kiša) Cilj: opisivanje veze između veličine i verovatnoće njene
Statistička analiza u hidrologiji Uvod Statistička analiza se primenjuje na podatke osmatranja hidroloških veličina (najčešće: protoka i kiša) Cilj: opisivanje veze između veličine i verovatnoće njene
Classroom Expectations
 АТ-8: Терминирање производно-технолошких ентитета Проф. др Зоран Миљковић Садржај Пројектовање флексибилних ; Математички модел за оптимизацију флексибилних ; Генетички алгоритми у оптимизацији флексибилних
АТ-8: Терминирање производно-технолошких ентитета Проф. др Зоран Миљковић Садржај Пројектовање флексибилних ; Математички модел за оптимизацију флексибилних ; Генетички алгоритми у оптимизацији флексибилних
MIP-heuristike (Matheuristike) Hibridi izmedu metaheurističkih i egzaktnih metoda Tatjana Davidović Matematički institut SANU
 MIP-heuristike (Matheuristike) Hibridi izmedu metaheurističkih i egzaktnih metoda Tatjana Davidović Matematički institut SANU http://www.mi.sanu.ac.rs/ tanjad (tanjad@mi.sanu.ac.rs) 21. januar 2013. Tatjana
MIP-heuristike (Matheuristike) Hibridi izmedu metaheurističkih i egzaktnih metoda Tatjana Davidović Matematički institut SANU http://www.mi.sanu.ac.rs/ tanjad (tanjad@mi.sanu.ac.rs) 21. januar 2013. Tatjana
1
 Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
AKVIZICIJA PODATAKA SA UREĐAJEM NI USB-6008 NI USB-6008 je jednostavni višenamjenski uređaj koji se koristi za akviziciju podataka (preko USBa), kao i
 AKVIZICIJA PODATAKA SA UREĐAJEM NI USB-6008 NI USB-6008 je jednostavni višenamjenski uređaj koji se koristi za akviziciju podataka (preko USBa), kao i za generisanje željenih izlaznih signala (slika 1).
AKVIZICIJA PODATAKA SA UREĐAJEM NI USB-6008 NI USB-6008 je jednostavni višenamjenski uređaj koji se koristi za akviziciju podataka (preko USBa), kao i za generisanje željenih izlaznih signala (slika 1).
Техничко решење: Софтвер за симулацију стохастичког ортогоналног мерила сигнала, његовог интеграла и диференцијала Руководилац пројекта: Владимир Вуји
 Техничко решење: Софтвер за симулацију стохастичког ортогоналног мерила сигнала, његовог интеграла и диференцијала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Велибор
Техничко решење: Софтвер за симулацију стохастичког ортогоналног мерила сигнала, његовог интеграла и диференцијала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Велибор
DISKRETNA MATEMATIKA
 DISKRETNA MATEMATIKA Kombinatorika Permutacije, kombinacije, varijacije, binomna formula Ivana Milosavljević - 1 - 1. KOMBINATORIKA PRINCIPI PREBROJAVANJA Predmet kombinatorike je raspoređivanje elemenata
DISKRETNA MATEMATIKA Kombinatorika Permutacije, kombinacije, varijacije, binomna formula Ivana Milosavljević - 1 - 1. KOMBINATORIKA PRINCIPI PREBROJAVANJA Predmet kombinatorike je raspoređivanje elemenata
РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена ) Прва година: ПРВА ГОДИНА - сви сем информатике Име пр
 РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена 23.01.2017.) Прва година: ПРВА ГОДИНА - сви сем информатике Име предмета Датум и термин одржавања писменог дела испита
РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена 23.01.2017.) Прва година: ПРВА ГОДИНА - сви сем информатике Име предмета Датум и термин одржавања писменог дела испита
Microsoft PowerPoint - C-4-1
 Pregled iskaza u C-u Izraz; Iskaz dodele, serijski komponovani iskaz; blok Uslovni iskazi i izrazi; složeno grananje Iterativni iskazi Iskaz dodele Promena vrednosti a = Ψ; Izračunava vrednost izraza Ψ,
Pregled iskaza u C-u Izraz; Iskaz dodele, serijski komponovani iskaz; blok Uslovni iskazi i izrazi; složeno grananje Iterativni iskazi Iskaz dodele Promena vrednosti a = Ψ; Izračunava vrednost izraza Ψ,
P11.3 Analiza zivotnog veka, Graf smetnji
 Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
Microsoft Word - III godina - EA - Metodi vjestacke inteligencije
 Школска година 2018/2019. Предмет Методи вјештачке интелигенције Шифра предмета 2284 Студијски програм Електроенергетика и аутоматика Циклус студија Година студија Семестар Број студената Број група за
Школска година 2018/2019. Предмет Методи вјештачке интелигенције Шифра предмета 2284 Студијски програм Електроенергетика и аутоматика Циклус студија Година студија Семестар Број студената Број група за
Microsoft Word - CAD sistemi
 U opštem slučaju, se mogu podeliti na 2D i 3D. 2D Prvo pojavljivanje 2D CAD sistema se dogodilo pre više od 30 godina. Do tada su inženjeri koristili table za crtanje (kulman), a zajednički jezik komuniciranja
U opštem slučaju, se mogu podeliti na 2D i 3D. 2D Prvo pojavljivanje 2D CAD sistema se dogodilo pre više od 30 godina. Do tada su inženjeri koristili table za crtanje (kulman), a zajednički jezik komuniciranja
Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]
![Microsoft PowerPoint - 03-Slozenost [Compatibility Mode] Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]](/thumbs/102/154806426.jpg) Сложеност алгоритама (Програмирање 2, глава 3, глава 4-4.3) Проблем: класа задатака истог типа Велики број различитих (коректних) алгоритама Величина (димензија) проблема нпр. количина података које треба
Сложеност алгоритама (Програмирање 2, глава 3, глава 4-4.3) Проблем: класа задатака истог типа Велики број различитих (коректних) алгоритама Величина (димензија) проблема нпр. количина података које треба
Slide 1
 Merni sistemi u računarstvu, http://automatika.etf.rs/sr/13e053msr Merna nesigurnost tipa A doc. dr Nadica Miljković, kabinet 68, nadica.miljkovic@etf.rs Prezentacija za ovo predavanje je skoro u potpunosti
Merni sistemi u računarstvu, http://automatika.etf.rs/sr/13e053msr Merna nesigurnost tipa A doc. dr Nadica Miljković, kabinet 68, nadica.miljkovic@etf.rs Prezentacija za ovo predavanje je skoro u potpunosti
Algoritmi
 Projektovanje algoritama L09.1. Topološko sortiranje Današnje teme Topološko sortiranje Povezanost grafa jako povezane komponente Minimum Spanning Trees (razapinjuće stablo) Lektira: 22. Elementary Graph
Projektovanje algoritama L09.1. Topološko sortiranje Današnje teme Topološko sortiranje Povezanost grafa jako povezane komponente Minimum Spanning Trees (razapinjuće stablo) Lektira: 22. Elementary Graph
Орт колоквијум
 II колоквијум из Основа рачунарске технике I - 27/28 (.6.28.) Р е ш е њ е Задатак На улазе x, x 2, x 3, x 4 комбинационе мреже, са излазом z, долази четворобитни BCD број. Ако број са улаза при дељењу
II колоквијум из Основа рачунарске технике I - 27/28 (.6.28.) Р е ш е њ е Задатак На улазе x, x 2, x 3, x 4 комбинационе мреже, са излазом z, долази четворобитни BCD број. Ако број са улаза при дељењу
P1.1 Analiza efikasnosti algoritama 1
 Analiza efikasnosti algoritama I Asimptotske notacije Master metoda (teorema) 1 Asimptotske notacije (1/2) Služe za opis vremena izvršenja algoritma T(n) gde je n N veličina ulaznih podataka npr. br. elemenata
Analiza efikasnosti algoritama I Asimptotske notacije Master metoda (teorema) 1 Asimptotske notacije (1/2) Služe za opis vremena izvršenja algoritma T(n) gde je n N veličina ulaznih podataka npr. br. elemenata
Pojačavači
 Programiranje u fizici Prirodno-matematički fakultet u Nišu Departman za fiziku dr Dejan S. Aleksić Programiranje u fizici dr Dejan S. Aleksić, vanredni profesor Kabinet 307 (treći sprat), lab. za elektroniku
Programiranje u fizici Prirodno-matematički fakultet u Nišu Departman za fiziku dr Dejan S. Aleksić Programiranje u fizici dr Dejan S. Aleksić, vanredni profesor Kabinet 307 (treći sprat), lab. za elektroniku
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe
 6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe, očekuje se da su koordinate celobrojne. U slučaju
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe, očekuje se da su koordinate celobrojne. U slučaju
EFIKASNO MODELIRANJE REALNIH OPTIMIZACIONIH PROBLEMA Tatjana Davidović Matematički institut SANU tanjad
 EFIKASNO MODELIRANJE REALNIH OPTIMIZACIONIH PROBLEMA Tatjana Davidović Matematički institut SANU http://www.mi.sanu.ac.rs/ tanjad (tanjad@mi.sanu.ac.rs) VII Simpozijum,,Matematika i primene 4. novembar
EFIKASNO MODELIRANJE REALNIH OPTIMIZACIONIH PROBLEMA Tatjana Davidović Matematički institut SANU http://www.mi.sanu.ac.rs/ tanjad (tanjad@mi.sanu.ac.rs) VII Simpozijum,,Matematika i primene 4. novembar
Slide 1
 Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 1: Увод и историјски развој теорије система UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES Катедра за управљање системима Наставници:
Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 1: Увод и историјски развој теорије система UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES Катедра за управљање системима Наставници:
Konstrukcija i analiza algoritama Nina Radojičić februar Analiza algoritama, rekurentne relacije 1 Definicija: Neka su f i g dve pozitivne fun
 Konstrukcija i analiza algoritama Nina Radojičić februar 2018. 1 Analiza algoritama, rekurentne relacije 1 Definicija: Neka su f i g dve pozitivne funkcije od argumenta n iz skupa N prirodnih brojeva.
Konstrukcija i analiza algoritama Nina Radojičić februar 2018. 1 Analiza algoritama, rekurentne relacije 1 Definicija: Neka su f i g dve pozitivne funkcije od argumenta n iz skupa N prirodnih brojeva.
STABILNOST SISTEMA
 STABILNOST SISTEMA Najvaznija osobina sistema automatskog upravljanja je stabilnost. Generalni zahtev koji se postavlja pred projektanta jeste da projektovani i realizovani sistem automatskog upravljanja
STABILNOST SISTEMA Najvaznija osobina sistema automatskog upravljanja je stabilnost. Generalni zahtev koji se postavlja pred projektanta jeste da projektovani i realizovani sistem automatskog upravljanja
ФАКУЛТЕТ ОРГАНИЗАЦИОНИХ НАУКА
 Питања за усмени део испита из Математике 3 I. ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ 1. Појам диференцијалне једначине. Пикарова теорема. - Написати општи и нормални облик диференцијалне једначине првог реда. - Дефинисати:
Питања за усмени део испита из Математике 3 I. ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ 1. Појам диференцијалне једначине. Пикарова теорема. - Написати општи и нормални облик диференцијалне једначине првог реда. - Дефинисати:
ТРОУГАО БРЗИНА и математичка неисправност Лоренцове трансформације у специјалној теорији релативности Александар Вукеља www.
 ТРОУГАО БРЗИНА и математичка неисправност Лоренцове трансформације у специјалној теорији релативности Александар Вукеља aleksandar@masstheory.org www.masstheory.org Август 2007 О ауторским правима: Дело
ТРОУГАО БРЗИНА и математичка неисправност Лоренцове трансформације у специјалној теорији релативности Александар Вукеља aleksandar@masstheory.org www.masstheory.org Август 2007 О ауторским правима: Дело
Microsoft Word - AIDA2kolokvijumRsmerResenja.doc
 Konstrukcija i analiza algoritama 2 (prvi kolokvijum, smer R) 1. a) Konstruisati AVL stablo od brojeva 100, 132, 134, 170, 180, 112, 188, 184, 181, 165 (2 poena) b) Konkatenacija je operacija nad dva skupa
Konstrukcija i analiza algoritama 2 (prvi kolokvijum, smer R) 1. a) Konstruisati AVL stablo od brojeva 100, 132, 134, 170, 180, 112, 188, 184, 181, 165 (2 poena) b) Konkatenacija je operacija nad dva skupa
Matematka 1 Zadaci za vežbe Oktobar Uvod 1.1. Izračunati vrednost izraza (bez upotrebe pomoćnih sredstava): ( ) [ a) : b) 3 3
 Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
Maksimalni protok kroz mrežu - Ford-Fulkerson, Edmonds-Karp
 Maksimalni protok kroz mrežu - Ford-Fulkerson, Edmonds-Karp PMF-MO Seminar iz kolegija Oblikovanje i analiza algoritama 22.1.2019. mrežu - Ford-Fulkerson, Edmonds-Karp 22.1.2019. 1 / 35 Uvod - definicije
Maksimalni protok kroz mrežu - Ford-Fulkerson, Edmonds-Karp PMF-MO Seminar iz kolegija Oblikovanje i analiza algoritama 22.1.2019. mrežu - Ford-Fulkerson, Edmonds-Karp 22.1.2019. 1 / 35 Uvod - definicije
TEORIJA SIGNALA I INFORMACIJA
 Multiple Input/Multiple Output sistemi MIMO sistemi Ulazi (pobude) Izlazi (odzivi) u 1 u 2 y 1 y 2 u k y r Obrada=Matematički model Načini realizacije: fizički sistemi (hardware) i algoritmi (software)
Multiple Input/Multiple Output sistemi MIMO sistemi Ulazi (pobude) Izlazi (odzivi) u 1 u 2 y 1 y 2 u k y r Obrada=Matematički model Načini realizacije: fizički sistemi (hardware) i algoritmi (software)
LAB PRAKTIKUM OR1 _ETR_
 UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA, TELEKOMUNIKACIJE I RAČUNARI PREDMET: OSNOVE RAČUNARSTVA 1 FOND ČASOVA: 2+1+1 LABORATORIJSKA VJEŽBA BROJ 1 NAZIV: REALIZACIJA
UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA, TELEKOMUNIKACIJE I RAČUNARI PREDMET: OSNOVE RAČUNARSTVA 1 FOND ČASOVA: 2+1+1 LABORATORIJSKA VJEŽBA BROJ 1 NAZIV: REALIZACIJA
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica
 Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
Verovatnoća - kolokvijum 17. decembar Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je
 Verovatnoća - kolokvijum 17. decembar 2016. 1. Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je 0.8. Ako je ispit težak, verovatnoća da se prvo pitanje
Verovatnoća - kolokvijum 17. decembar 2016. 1. Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je 0.8. Ako je ispit težak, verovatnoća da se prvo pitanje
VEŽBE IZ OPERACIONIH ISTRAŽIVANJA
 VEŽBE IZ OPERACIONIH ISTRAŽIVANJA Glava 4 1. Metoda grananja i odsecanja 2. Metoda grananja i ograničavanja 3. Metoda implicitnog prebrojavanja MARIJA IVANOVIĆ marijai@math.rs Metoda grananja i odsecanja
VEŽBE IZ OPERACIONIH ISTRAŽIVANJA Glava 4 1. Metoda grananja i odsecanja 2. Metoda grananja i ograničavanja 3. Metoda implicitnog prebrojavanja MARIJA IVANOVIĆ marijai@math.rs Metoda grananja i odsecanja
Tutoring System for Distance Learning of Java Programming Language
 Niz (array) Nizovi Niz je lista elemenata istog tipa sa zajedničkim imenom. Redosled elemenata u nizovnoj strukturi je bitan. Konkretnom elementu niza pristupa se preko zajedničkog imena niza i konkretne
Niz (array) Nizovi Niz je lista elemenata istog tipa sa zajedničkim imenom. Redosled elemenata u nizovnoj strukturi je bitan. Konkretnom elementu niza pristupa se preko zajedničkog imena niza i konkretne
08 RSA1
 Преглед ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције RSA алгоритам Биће објашњено: RSA алгоритам алгоритам прорачунски аспекти ефикасност коришћењем јавног кључа генерисање кључа сигурност проблем
Преглед ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције RSA алгоритам Биће објашњено: RSA алгоритам алгоритам прорачунски аспекти ефикасност коришћењем јавног кључа генерисање кључа сигурност проблем
Програмирај!
 Листе Поред појединачних вредности исказаних бројем или ниском карактера, често је потребно забележити већи скуп вредности које су на неки начин повезане, као, на пример, имена у списку путника у неком
Листе Поред појединачних вредности исказаних бројем или ниском карактера, често је потребно забележити већи скуп вредности које су на неки начин повезане, као, на пример, имена у списку путника у неком
SKRIPTE EKOF 2019/20 skripteekof.com Lekcija 1: Brojevni izrazi Lekcija 1: Brojevni izrazi Pregled lekcije U okviru ove lekcije imaćete priliku da nau
 Lekcija : Brojevni izrazi Pregled lekcije U okviru ove lekcije imaćete priliku da naučite sledeće: osnovni pojmovi o razlomcima proširivanje, skraćivanje, upoređivanje; zapis razlomka u okviru mešovitog
Lekcija : Brojevni izrazi Pregled lekcije U okviru ove lekcije imaćete priliku da naučite sledeće: osnovni pojmovi o razlomcima proširivanje, skraćivanje, upoređivanje; zapis razlomka u okviru mešovitog
MAZALICA DUŠKA.pdf
 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ELEKTROTEHNIČKI FAKULTET Sveučilišni studij OPTIMIRANJE INTEGRACIJE MALIH ELEKTRANA U DISTRIBUCIJSKU MREŽU Diplomski rad Duška Mazalica Osijek, 2014. SADRŽAJ
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ELEKTROTEHNIČKI FAKULTET Sveučilišni studij OPTIMIRANJE INTEGRACIJE MALIH ELEKTRANA U DISTRIBUCIJSKU MREŽU Diplomski rad Duška Mazalica Osijek, 2014. SADRŽAJ
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић
 Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Драган Пејић, Бојан Вујичић, Небојша Пјевалица,
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Драган Пејић, Бојан Вујичић, Небојша Пјевалица,
Рачунарска интелигенција
 Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Uvod u računarstvo 2+2
 Programiranje 2 doc.dr.sc. Goranka Nogo PMF Matematički odsjek, Zagreb Kontakt ured: 228, drugi kat e-mail: nogo@math.hr konzultacije: četvrtak, 12:00-14:00 petak, 11:00-12:00 neki drugi termin, uz prethodni
Programiranje 2 doc.dr.sc. Goranka Nogo PMF Matematički odsjek, Zagreb Kontakt ured: 228, drugi kat e-mail: nogo@math.hr konzultacije: četvrtak, 12:00-14:00 petak, 11:00-12:00 neki drugi termin, uz prethodni
Konstrukcija i analiza algoritama vežbe 10 Nina Radojičić 15. decembar Algoritamske strategije - podeli pa vladaj (divide and conquer) Ova stra
 Konstrukcija i analiza algoritama vežbe 10 Nina Radojičić 15. decembar 2016 1 Algoritamske strategije - podeli pa vladaj (divide and conquer) Ova strategija rekurzivno razbija problem na 2 ili više potproblema
Konstrukcija i analiza algoritama vežbe 10 Nina Radojičić 15. decembar 2016 1 Algoritamske strategije - podeli pa vladaj (divide and conquer) Ova strategija rekurzivno razbija problem na 2 ili više potproblema
Електротехнички факултет Универзитета у Београду Катедра за рачунарску технику и информатику Kолоквијум из Интелигентних система Колоквију
 Електротехнички факултет Универзитета у Београду 19.11.017. Катедра за рачунарску технику и информатику Kолоквијум из Интелигентних система Колоквијум траје h. Напуштање сале дозвољено је након 1h. Употреба
Електротехнички факултет Универзитета у Београду 19.11.017. Катедра за рачунарску технику и информатику Kолоквијум из Интелигентних система Колоквијум траје h. Напуштање сале дозвољено је након 1h. Употреба
Veeeeeliki brojevi
 Matematička gimnazija Nedelja informatike 3 12. decembar 2016. Uvod Postoji 10 tipova ljudi na svetu, oni koji razumeju binarni sistem, oni koji ne razumeju binarni sistem i oni koji nisu očekivali šalu
Matematička gimnazija Nedelja informatike 3 12. decembar 2016. Uvod Postoji 10 tipova ljudi na svetu, oni koji razumeju binarni sistem, oni koji ne razumeju binarni sistem i oni koji nisu očekivali šalu
Projektovanje tehnoloških procesa
 ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА Департман за производно машинство Пројектовање технолошких процеса Тема: Др Мијодраг Милошевић Технолошки процеси израде производа Део производног процеса у коме се врши измена
ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА Департман за производно машинство Пројектовање технолошких процеса Тема: Др Мијодраг Милошевић Технолошки процеси израде производа Део производног процеса у коме се врши измена
Microsoft PowerPoint - jkoren10.ppt
 Dickey-Fuller-ov test jediničnog korena Osnovna ideja Različite determinističke komponente Izračunavanje test-statistike Pravilo odlučivanja Određivanje broja jediničnih korena Algoritam testiranja Prošireni
Dickey-Fuller-ov test jediničnog korena Osnovna ideja Različite determinističke komponente Izračunavanje test-statistike Pravilo odlučivanja Određivanje broja jediničnih korena Algoritam testiranja Prošireni
Slide 1
 Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
МОДЕЛ КОНТРОЛНЕ ВЕЖБЕ Информатика и рачунарство за шести разред разред Наставна тема: Редни број часа: 8. РАЧУНАРСТВО Циљ часа: Теститарање постигнућа
 МОДЕЛ КОНТРОЛНЕ ВЕЖБЕ Наставна тема: Редни број часа: 8. РАЧУНАРСТВО Циљ часа: Теститарање постигнућа ученика из области: Линијска структура алгоритма, петља for, гранање, петља while, угњежђене петље.
МОДЕЛ КОНТРОЛНЕ ВЕЖБЕ Наставна тема: Редни број часа: 8. РАЧУНАРСТВО Циљ часа: Теститарање постигнућа ученика из области: Линијска структура алгоритма, петља for, гранање, петља while, угњежђене петље.
Računarski praktikum I - Vježbe 11 - Funktori
 Prirodoslovno-matematički fakultet Matematički odsjek Sveučilište u Zagrebu RAČUNARSKI PRAKTIKUM I Vježbe 11 - Funktori v2018/2019. Sastavio: Zvonimir Bujanović Funkcijski objekti (funktori) Objekt klase
Prirodoslovno-matematički fakultet Matematički odsjek Sveučilište u Zagrebu RAČUNARSKI PRAKTIKUM I Vježbe 11 - Funktori v2018/2019. Sastavio: Zvonimir Bujanović Funkcijski objekti (funktori) Objekt klase
Algoritmi i arhitekture DSP I
 Univerzitet u Novom Sadu Fakultet Tehničkih Nauka Katedra za računarsku tehniku i međuračunarske komunikacije Algoritmi i arhitekture DSP I INTERNA ORGANIACIJA DIGITALNOG PROCESORA A OBRADU SIGNALA INTERNA
Univerzitet u Novom Sadu Fakultet Tehničkih Nauka Katedra za računarsku tehniku i međuračunarske komunikacije Algoritmi i arhitekture DSP I INTERNA ORGANIACIJA DIGITALNOG PROCESORA A OBRADU SIGNALA INTERNA
Skripte2013
 Chapter 2 Algebarske strukture Preslikivanje f : A n! A se naziva n-arna operacija na skupu A Ako je n =2, kažemo da je f : A A! A binarna operacija na A Kažemo da je operacija f arnosti n, u oznaci ar
Chapter 2 Algebarske strukture Preslikivanje f : A n! A se naziva n-arna operacija na skupu A Ako je n =2, kažemo da je f : A A! A binarna operacija na A Kažemo da je operacija f arnosti n, u oznaci ar
DR DRAGOŚ CVETKOVIC DR SLOBODAN SIMIC DISKRETNA MATEMATIKA MATEMATIKA ZA KOMPJUTERSKE NAUKĘ DRUGO ISPRAYLJENO I PROSIRENO IZDANJE HMUJ
 DR DRAGOŚ CVETKOVIC DR SLOBODAN SIMIC DISKRETNA MATEMATIKA MATEMATIKA ZA KOMPJUTERSKE NAUKĘ DRUGO ISPRAYLJENO I PROSIRENO IZDANJE HMUJ Sadrżaj Predgovor Iz predgovora prvoni izdanju knjige "Diskretne mateiuatićke
DR DRAGOŚ CVETKOVIC DR SLOBODAN SIMIC DISKRETNA MATEMATIKA MATEMATIKA ZA KOMPJUTERSKE NAUKĘ DRUGO ISPRAYLJENO I PROSIRENO IZDANJE HMUJ Sadrżaj Predgovor Iz predgovora prvoni izdanju knjige "Diskretne mateiuatićke
Neuronske mreže
 Neuronske mreže: Genetički algoritmi Prof. dr. sc. Sven Lončarić Fakultet elektrotehnike i računarstva sven.loncaric@fer.hr http://ipg.zesoi.fer.hr 1 Uvod U mnogim primjenama pojavljuje se problem optimizacije
Neuronske mreže: Genetički algoritmi Prof. dr. sc. Sven Lončarić Fakultet elektrotehnike i računarstva sven.loncaric@fer.hr http://ipg.zesoi.fer.hr 1 Uvod U mnogim primjenama pojavljuje se problem optimizacije
Упутство за пријављивање испита путем интернета Да би студент могао да пријави испит путем интернета мора прво да се пријави. Пријављивање се врши у п
 Упутство за пријављивање испита путем интернета Да би студент могао да пријави испит путем интернета мора прво да се пријави. Пријављивање се врши у посебном дијалог-прозору до кога се долази линком есервис
Упутство за пријављивање испита путем интернета Да би студент могао да пријави испит путем интернета мора прво да се пријави. Пријављивање се врши у посебном дијалог-прозору до кога се долази линком есервис
Microsoft Word - ZadaciSeminarski.doc
 Format izrade rada:.pdf,.html Programski jezik: C/C++ Rok izrade: 7.12.2013. Način predaje: e-mail (C file + pdf/html opis resenja ili URL kompletne arhive) Pretpostavka: 100 MIPS sistem za evaluaciju
Format izrade rada:.pdf,.html Programski jezik: C/C++ Rok izrade: 7.12.2013. Način predaje: e-mail (C file + pdf/html opis resenja ili URL kompletne arhive) Pretpostavka: 100 MIPS sistem za evaluaciju
2015_k2_z12.dvi
 OBLIKOVANJE I ANALIZA ALGORITAMA 2. kolokvij 27. 1. 2016. Skice rješenja prva dva zadatka 1. (20) Zadano je n poslova. Svaki posao je zadan kao vremenski interval realnih brojeva, P i = [p i,k i ],zai
OBLIKOVANJE I ANALIZA ALGORITAMA 2. kolokvij 27. 1. 2016. Skice rješenja prva dva zadatka 1. (20) Zadano je n poslova. Svaki posao je zadan kao vremenski interval realnih brojeva, P i = [p i,k i ],zai
ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 2006/2007 године I разред
 ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 006/007 године разред. Електрични систем се састоји из отпорника повезаних тако
ДРУШТВО ФИЗИЧАРА СРБИЈЕ МИНИСТАРСТВО ПРОСВЕТЕ И СПОРТА РЕПУБЛИКЕ СРБИЈЕ Задаци за републичко такмичење ученика средњих школа 006/007 године разред. Електрични систем се састоји из отпорника повезаних тако
Univerzitet u Novom Sadu Tehnički fakultet Mihajlo Pupin Zrenjanin Seminarski rad Predmet: Konkuretno programiranje doc. dr Dejan Lacmanovic Zorica Br
 Univerzitet u Novom Sadu Tehnički fakultet Mihajlo Pupin Zrenjanin Seminarski rad Predmet: Konkuretno programiranje doc. dr Dejan Lacmanovic Zorica Brkić SI 29/15 Zrenjanin 2018. Softversko inženjerstvo
Univerzitet u Novom Sadu Tehnički fakultet Mihajlo Pupin Zrenjanin Seminarski rad Predmet: Konkuretno programiranje doc. dr Dejan Lacmanovic Zorica Brkić SI 29/15 Zrenjanin 2018. Softversko inženjerstvo
P2.1 Projektovanje paralelnih algoritama 1
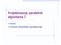 Projektovanje paralelnih algoritama I Uvod Osnove dinamičke paralelizacije 1 Primer: Fibonačijev niz Primer rekurz. računanja Fibonačijevih brojeva: F 0 = 0; F 1 = 1; F i = F i -1 + F i -2 za i 2 Algoritam
Projektovanje paralelnih algoritama I Uvod Osnove dinamičke paralelizacije 1 Primer: Fibonačijev niz Primer rekurz. računanja Fibonačijevih brojeva: F 0 = 0; F 1 = 1; F i = F i -1 + F i -2 za i 2 Algoritam
Microsoft PowerPoint - PS9_Linijski raspored i redosled
 ОДРЕЂИВАЊЕ ОДГОВАРАЈУЋЕГ ЛИНИЈСКОГ РАСПОРЕДА РАДНИХ МЕСТА ОДРЕЂИВАЊЕ ОДГОВАРАЈУЋЕГ ЛИНИЈСКОГ РАСПОРЕДА РАДНИХ МЕСТА Код серијске и великосеријске производње ФУНКЦИЈА ЦИЉА (КРИТЕРИЈУМ ОПТИМАЛНОСТИ) > Минимални
ОДРЕЂИВАЊЕ ОДГОВАРАЈУЋЕГ ЛИНИЈСКОГ РАСПОРЕДА РАДНИХ МЕСТА ОДРЕЂИВАЊЕ ОДГОВАРАЈУЋЕГ ЛИНИЈСКОГ РАСПОРЕДА РАДНИХ МЕСТА Код серијске и великосеријске производње ФУНКЦИЈА ЦИЉА (КРИТЕРИЈУМ ОПТИМАЛНОСТИ) > Минимални
Microsoft Word - Elektrijada_V2_2014_final.doc
 I област. У колу сталне струје са слике када је и = V, амперметар показује I =. Одредити показивање амперметра I када је = 3V и = 4,5V. Решење: а) I = ) I =,5 c) I =,5 d) I = 7,5 3 3 Слика. I област. Дата
I област. У колу сталне струје са слике када је и = V, амперметар показује I =. Одредити показивање амперметра I када је = 3V и = 4,5V. Решење: а) I = ) I =,5 c) I =,5 d) I = 7,5 3 3 Слика. I област. Дата
PITANJA I ZADACI ZA II KOLOKVIJUM IZ MATEMATIKE I Pitanja o nizovima Nizovi Realni niz i njegov podniz. Tačka nagomilavanja niza i granična vrednost(l
 PITANJA I ZADACI ZA II KOLOKVIJUM IZ MATEMATIKE I Pitanja o nizovima Nizovi Realni niz i njegov podniz. Tačka nagomilavanja niza i granična vrednost(limes) niza. Svojstva konvergentnih nizova, posebno
PITANJA I ZADACI ZA II KOLOKVIJUM IZ MATEMATIKE I Pitanja o nizovima Nizovi Realni niz i njegov podniz. Tačka nagomilavanja niza i granična vrednost(limes) niza. Svojstva konvergentnih nizova, posebno
Microsoft PowerPoint - NAD IR OS pravila 2017.pptx
 Нумеричка анализа и дискретна математика 2017/2018 ИР, ОС ванр. проф. др Бранко Малешевић, доц. др Ивана Јововић ванр. проф. др Синиша Јешић, доц. др Наташа Ћировић Настава Курс Нумеричка анализа и дискретна
Нумеричка анализа и дискретна математика 2017/2018 ИР, ОС ванр. проф. др Бранко Малешевић, доц. др Ивана Јововић ванр. проф. др Синиша Јешић, доц. др Наташа Ћировић Настава Курс Нумеричка анализа и дискретна
Задатак 4: Центрифугална пумпа познате карактеристике при n = 2900 min -1 ради на инсталацији приказаној на слици и потискује воду из резервоара А у р
 Задатак 4: Центрифугална пумпа познате карактеристике при n = 900 min -1 ради на инсталацији приказаној на слици и потискује воду из резервоара А у резервоар B. Непосредно на излазу из пумпе постављен
Задатак 4: Центрифугална пумпа познате карактеристике при n = 900 min -1 ради на инсталацији приказаној на слици и потискује воду из резервоара А у резервоар B. Непосредно на излазу из пумпе постављен
Microsoft Word - 1. REALNI BROJEVI- formulice
 REALNI BROJEVI Skup prirodnih brojeva je N={1,2,3,4,,6,7, } Ako skupu prirodnih brojeva dodamo i nulu onda imamo skup N 0 ={0,1,2,3, } Skup celih brojeva je Z = {,-3,-2,-1,0,1,2,3, } Skup racionalnih brojeva
REALNI BROJEVI Skup prirodnih brojeva je N={1,2,3,4,,6,7, } Ako skupu prirodnih brojeva dodamo i nulu onda imamo skup N 0 ={0,1,2,3, } Skup celih brojeva je Z = {,-3,-2,-1,0,1,2,3, } Skup racionalnih brojeva
Razvoj programa, Code::Blocks, struktura programa, printf, scanf, konverzioni karakteri predavač: Nadežda Jakšić
 Razvoj programa, Code::Blocks, struktura programa, printf, scanf, konverzioni karakteri predavač: Nadežda Jakšić projektni zadatak projektovanje programa (algoritmi) pisanje programskog koda, izvorni kod,
Razvoj programa, Code::Blocks, struktura programa, printf, scanf, konverzioni karakteri predavač: Nadežda Jakšić projektni zadatak projektovanje programa (algoritmi) pisanje programskog koda, izvorni kod,
13E114PAR, 13S113PAR DOMAĆI ZADATAK 2018/2019. Cilj domaćeg zadatka je formiranje petlje softverske protočnosti za minimalni broj ciklusa.
 13E114PAR, 13S113PAR 29.04.2019. DOMAĆI ZADATAK 2018/2019. Cilj domaćeg zadatka je formiranje petlje softverske protočnosti za minimalni broj ciklusa. U okviru svake grupe data je doall ili doacross petlja
13E114PAR, 13S113PAR 29.04.2019. DOMAĆI ZADATAK 2018/2019. Cilj domaćeg zadatka je formiranje petlje softverske protočnosti za minimalni broj ciklusa. U okviru svake grupe data je doall ili doacross petlja
Талесова 1 теорема и примене - неки задаци из збирке Дефинициjа 1: Нека су a и b две дужи чиjе су дужине изражене преко мерне jединице k > 0, тако да
 Талесова 1 теорема и примене - неки задаци из збирке Дефинициjа 1: Нека су и две дужи чиjе су дужине изражене преко мерне jединице k > 0, тако да jе m k и n k, где су m, n > 0. Тада кажемо да су дужи и
Талесова 1 теорема и примене - неки задаци из збирке Дефинициjа 1: Нека су и две дужи чиjе су дужине изражене преко мерне jединице k > 0, тако да jе m k и n k, где су m, n > 0. Тада кажемо да су дужи и
Drveta odlucivanja - algoritmi
 Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Uvod Algoritmi (Iterative Dichotomiser 3) C5.0 (Classification And Regression Trees) (CHi-squared Automatic Interaction Detection) Exhaustive (Quick,
Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Uvod Algoritmi (Iterative Dichotomiser 3) C5.0 (Classification And Regression Trees) (CHi-squared Automatic Interaction Detection) Exhaustive (Quick,
Programiranje u C-u ili C++-u Pseudo-slučajni brojevi; Dinamička alokacija memorije 1 ZADACI SA ČASA Zadatak 1 Napraviti funkciju koja generišlučajan
 Programiranje u C-u ili C++-u Pseudo-slučajni brojevi; Dinamička alokacija memorije 1 ZADACI SA ČASA Zadatak 1 Napraviti funkciju koja generišlučajan realan broj od 0 i 1. Na standardni izlaz ispisati
Programiranje u C-u ili C++-u Pseudo-slučajni brojevi; Dinamička alokacija memorije 1 ZADACI SA ČASA Zadatak 1 Napraviti funkciju koja generišlučajan realan broj od 0 i 1. Na standardni izlaz ispisati
Microsoft Word - 1.Operacije i zakoni operacija
 1. Operacije i zakoni operacija Neka je S neprazan skup. Operacija dužine n skupa S jeste svako preslikavanje : n n f S S ( S = S S S... S) Ako je n = 1, onda operaciju nazivamo unarna. ( f : S S ) Ako
1. Operacije i zakoni operacija Neka je S neprazan skup. Operacija dužine n skupa S jeste svako preslikavanje : n n f S S ( S = S S S... S) Ako je n = 1, onda operaciju nazivamo unarna. ( f : S S ) Ako
SEMINAR
 1. Cilj vežbe Lekcija 9 Akvizicija i osnovna obrada slike u LabVIEW Cilj vežbe je da studente upozna sa: Akvizicijom slike. Osnovnim koracima pri obradi slike Zadatak 9.1. Povezati USB kameru i kreirati
1. Cilj vežbe Lekcija 9 Akvizicija i osnovna obrada slike u LabVIEW Cilj vežbe je da studente upozna sa: Akvizicijom slike. Osnovnim koracima pri obradi slike Zadatak 9.1. Povezati USB kameru i kreirati
PROGRAMIRANJE Program je niz naredbi razumljivih računalu koje rješavaju neki problem. Algoritam je postupak raščlanjivanja problema na jednostavnije
 PROGRAMIRANJE Program je niz naredbi razumljivih računalu koje rješavaju neki problem. Algoritam je postupak raščlanjivanja problema na jednostavnije korake. Uz dobro razrađen algoritam neku radnju ćemo
PROGRAMIRANJE Program je niz naredbi razumljivih računalu koje rješavaju neki problem. Algoritam je postupak raščlanjivanja problema na jednostavnije korake. Uz dobro razrađen algoritam neku radnju ćemo
Optimizacija
 Optimizacija 1 / 43 2 / 43 Uvod u optimizaciju Zadana funkcija Uvod u optimizaciju f : R n R Cilj: Naći x, točku minimuma funkcije f : - Problem je jednostavno opisati x = arg min x R n f (x). - Rješavanje
Optimizacija 1 / 43 2 / 43 Uvod u optimizaciju Zadana funkcija Uvod u optimizaciju f : R n R Cilj: Naći x, točku minimuma funkcije f : - Problem je jednostavno opisati x = arg min x R n f (x). - Rješavanje
Oblikovanje i analiza algoritama 4. predavanje Saša Singer web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb OAA 2017, 4. pr
 Oblikovanje i analiza algoritama 4. predavanje Saša Singer singer@math.hr web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb OAA 2017, 4. predavanje p. 1/69 Sadržaj predavanja Složenost u praksi
Oblikovanje i analiza algoritama 4. predavanje Saša Singer singer@math.hr web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb OAA 2017, 4. predavanje p. 1/69 Sadržaj predavanja Složenost u praksi
FTN Novi Sad Katedra za motore i vozila Potrošnja goriva Teorija kretanja drumskih vozila Potrošnja goriva
 Ključni faktori: 1. ENERGIJA potrebna za kretanje vozila na određenoj deonici puta Povećanje E K pri ubrzavanju, pri penjanju, kompenzacija energetskih gubitaka usled dejstva F f i F W Zavisi od parametara
Ključni faktori: 1. ENERGIJA potrebna za kretanje vozila na određenoj deonici puta Povećanje E K pri ubrzavanju, pri penjanju, kompenzacija energetskih gubitaka usled dejstva F f i F W Zavisi od parametara
Microsoft Word - Raspored ispita Jun.doc
 FAKULTET ORGANIZACIONIH NAUKA KONAČAN RASPORED ISPITA ZA JUNSKI ISPITNI ROK 8. GODINE Predmet Od. P/U Datum Sale Napomena Akcionarstvo i berzansko poslovanje ME U 21/06/8---- Arhitektura računara i oper.
FAKULTET ORGANIZACIONIH NAUKA KONAČAN RASPORED ISPITA ZA JUNSKI ISPITNI ROK 8. GODINE Predmet Od. P/U Datum Sale Napomena Akcionarstvo i berzansko poslovanje ME U 21/06/8---- Arhitektura računara i oper.
Microsoft Word - 4.Ucenik razlikuje direktno i obrnuto proporcionalne velicine, zna linearnu funkciju i graficki interpretira n
 4. UČENIK RAZLIKUJE DIREKTNO I OBRNUTO PROPORCIONALNE VELIČINE, ZNA LINEARNU FUNKCIJU I GRAFIČKI INTERPRETIRA NJENA SVOJSTVA U fajlu 4. iz srednjeg nivoa smo se upoznali sa postupkom rada kada je u pitanju
4. UČENIK RAZLIKUJE DIREKTNO I OBRNUTO PROPORCIONALNE VELIČINE, ZNA LINEARNU FUNKCIJU I GRAFIČKI INTERPRETIRA NJENA SVOJSTVA U fajlu 4. iz srednjeg nivoa smo se upoznali sa postupkom rada kada je u pitanju
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K.
 1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K. Elementi a k K su koeficijenti polinoma P (x). Ako
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K. Elementi a k K su koeficijenti polinoma P (x). Ako
PLAN I PROGRAM ZA DOPUNSKU (PRODUŽNU) NASTAVU IZ MATEMATIKE (za 1. razred)
 PLAN I PROGRAM ZA DOPUNSKU (PRODUŽNU) NASTAVU IZ MATEMATIKE (za 1. razred) Učenik prvog razreda treba ostvarit sljedeće minimalne standarde 1. SKUP REALNIH BROJEVA -razlikovati brojevne skupove i njihove
PLAN I PROGRAM ZA DOPUNSKU (PRODUŽNU) NASTAVU IZ MATEMATIKE (za 1. razred) Učenik prvog razreda treba ostvarit sljedeće minimalne standarde 1. SKUP REALNIH BROJEVA -razlikovati brojevne skupove i njihove
Орт колоквијум
 Испит из Основа рачунарске технике - / (6.6.. Р е ш е њ е Задатак Комбинациона мрежа има пет улаза, по два за број освојених сетова тенисера и један сигнал који одлучује ко је бољи уколико је резултат
Испит из Основа рачунарске технике - / (6.6.. Р е ш е њ е Задатак Комбинациона мрежа има пет улаза, по два за број освојених сетова тенисера и један сигнал који одлучује ко је бољи уколико је резултат
Kombinatorno testiranje
 Kombinatorno testiranje Uvod Na ponašanje aplikacije utiče puno faktora, npr. ulazne vrednosti, konfiguracije okruženja. Tehnike kao što je podela na klase ekvivalencije ili analiza graničnih vrednosti
Kombinatorno testiranje Uvod Na ponašanje aplikacije utiče puno faktora, npr. ulazne vrednosti, konfiguracije okruženja. Tehnike kao što je podela na klase ekvivalencije ili analiza graničnih vrednosti
ЈЕДАН НОВИ ПРИСТУП У ПРЕВОЂЕЊУ ИЗ BPMN а У BPEL ONE NEW APPROACH IN TRANSLATING FROM BPMN TO BPEL Александар Недељковић Факултет организационих наука,
 ЈЕДАН НОВИ ПРИСТУП У ПРЕВОЂЕЊУ ИЗ BPMN а У BPEL ONE NEW APPROACH IN TRANSLATING FROM BPMN TO BPEL Александар Недељковић Факултет организационих наука, Београд Садржај BPMN и BPEL су два највише коришћена
ЈЕДАН НОВИ ПРИСТУП У ПРЕВОЂЕЊУ ИЗ BPMN а У BPEL ONE NEW APPROACH IN TRANSLATING FROM BPMN TO BPEL Александар Недељковић Факултет организационих наука, Београд Садржај BPMN и BPEL су два највише коришћена
ЛИНЕАРНА ФУНКЦИЈА ЛИНЕАРНА ФУНКЦИЈА у = kх + n А утврди 1. Које од наведених функција су линеарне: а) у = 2х; б) у = 4х; в) у = 2х 7; г) у = 2 5 x; д)
 ЛИНЕАРНА ФУНКЦИЈА ЛИНЕАРНА ФУНКЦИЈА у = kх + n А утврди 1. Које од наведених функција су линеарне: а) у = х; б) у = 4х; в) у = х 7; г) у = 5 x; д) у = 5x ; ђ) у = х + х; е) у = x + 5; ж) у = 5 x ; з) у
ЛИНЕАРНА ФУНКЦИЈА ЛИНЕАРНА ФУНКЦИЈА у = kх + n А утврди 1. Које од наведених функција су линеарне: а) у = х; б) у = 4х; в) у = х 7; г) у = 5 x; д) у = 5x ; ђ) у = х + х; е) у = x + 5; ж) у = 5 x ; з) у
FAKULTET ORGANIZACIONIH NAUKA
 FAKULTET ORGANIZACIONIH NAUKA KONAČAN RASPORED ISPITA ZA OKTOBARSKI ISPITNI ROK (po datumu) Predmet Odsek P/U Datum Sala Upravljanje kvalitetom dokumentacije UK P 22/09/2007----09:00 RC Informacioni sistemi
FAKULTET ORGANIZACIONIH NAUKA KONAČAN RASPORED ISPITA ZA OKTOBARSKI ISPITNI ROK (po datumu) Predmet Odsek P/U Datum Sala Upravljanje kvalitetom dokumentacije UK P 22/09/2007----09:00 RC Informacioni sistemi
Postavka 2: Osnovni graf algoritmi 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch
 Postavka 2: Osnovni graf algoritmi 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch A1 Slanje svima preko fiksiranog razapinjućeg stabla
Postavka 2: Osnovni graf algoritmi 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch A1 Slanje svima preko fiksiranog razapinjućeg stabla
Profajliranje ivica: Knutov algoritam i njegova unapredenja Seminarski rad u okviru kursa Verifikacija softvera Matematički fakultet Nevena Nikolić, 1
 Profajliranje ivica: Knutov algoritam i njegova unapredenja Seminarski rad u okviru kursa Verifikacija softvera Matematički fakultet Nevena Nikolić, 1021/2018 nevena134@hotmail.com 9. decembar 2018 Sažetak
Profajliranje ivica: Knutov algoritam i njegova unapredenja Seminarski rad u okviru kursa Verifikacija softvera Matematički fakultet Nevena Nikolić, 1021/2018 nevena134@hotmail.com 9. decembar 2018 Sažetak
Problemi zadovoljavanja ogranicenja.
 I122 Osnove umjetne inteligencije Tema:. 7.1.2016. predavač: Darija Marković asistent: Darija Marković 1 I122 Osnove umjetne inteligencije. 2/26 (PZO) Problem zadovoljavanja ograničenja sastoji se od 3
I122 Osnove umjetne inteligencije Tema:. 7.1.2016. predavač: Darija Marković asistent: Darija Marković 1 I122 Osnove umjetne inteligencije. 2/26 (PZO) Problem zadovoljavanja ograničenja sastoji se od 3
Microsoft PowerPoint - 10 PEK EMT Logicka simulacija 1 od 2 (2012).ppt [Compatibility Mode]
![Microsoft PowerPoint - 10 PEK EMT Logicka simulacija 1 od 2 (2012).ppt [Compatibility Mode] Microsoft PowerPoint - 10 PEK EMT Logicka simulacija 1 od 2 (2012).ppt [Compatibility Mode]](/thumbs/101/150310241.jpg) ij Cilj: Dobiti što više informacija o ponašanju digitalnih kola za što kraće vreme. Metod: - Detaljni talasni oblik signala prikazati samo na nivou logičkih stanja. - Simulirati ponašanje kola samo u
ij Cilj: Dobiti što više informacija o ponašanju digitalnih kola za što kraće vreme. Metod: - Detaljni talasni oblik signala prikazati samo na nivou logičkih stanja. - Simulirati ponašanje kola samo u
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ и технолошког развоја ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВН
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ и технолошког развоја ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2018/2019. година
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ и технолошког развоја ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2018/2019. година
ПА-4 Машинско учење-алгоритми машинског учења
 ПА-4 Машинско учење-алгоритми машинског учења Машинско учење увод и основни појмови Деф: the desgn and development of algorthms that allow computers to mprove ther performance over tme based on data sensor
ПА-4 Машинско учење-алгоритми машинског учења Машинско учење увод и основни појмови Деф: the desgn and development of algorthms that allow computers to mprove ther performance over tme based on data sensor
Увод у организацију и архитектуру рачунара 1
 Увод у организацију и архитектуру рачунара 2 Александар Картељ kartelj@matf.bg.ac.rs Напомена: садржај ових слајдова је преузет од проф. Саше Малкова Увод у организацију и архитектуру рачунара 2 1 Секвенцијалне
Увод у организацију и архитектуру рачунара 2 Александар Картељ kartelj@matf.bg.ac.rs Напомена: садржај ових слајдова је преузет од проф. Саше Малкова Увод у организацију и архитектуру рачунара 2 1 Секвенцијалне
Microsoft Word - 14Celobrojno.doc
 3. CELOBROJNO LINEARNO PROGAMIRANJE 3.1. MODELI CELOBROJNOG PROGRAMIRANJA Svaki matematički model, sa funkcijom kriterijuma minimuma ili maksimuma, u kojem bar jedna primarna promenljiva mora biti celobrojna
3. CELOBROJNO LINEARNO PROGAMIRANJE 3.1. MODELI CELOBROJNOG PROGRAMIRANJA Svaki matematički model, sa funkcijom kriterijuma minimuma ili maksimuma, u kojem bar jedna primarna promenljiva mora biti celobrojna
Microsoft PowerPoint - vezbe 4. Merenja u telekomunikacionim mrežama
 Merenja u telekomunikacionim mrežama Merenja telefonskog saobraćaja Primer 1 - TCBH Na osnovu najviših vrednosti intenziteta saobraćaja datih za 20 mernih dana (tabela), pomoću metode TCBH, pronaći čas
Merenja u telekomunikacionim mrežama Merenja telefonskog saobraćaja Primer 1 - TCBH Na osnovu najviših vrednosti intenziteta saobraćaja datih za 20 mernih dana (tabela), pomoću metode TCBH, pronaći čas
Microsoft Word - ASIMPTOTE FUNKCIJE.doc
 ASIMPTOTE FUNKCIJE (PONAŠANJE FUNKCIJE NA KRAJEVIMA OBLASTI DEFINISANOSTI) Ovo je jedna od najznačajnijih tačaka u ispitivanju toka funkcije. Neki profesori zahtevaju da se asimptote rade kao. tačka u
ASIMPTOTE FUNKCIJE (PONAŠANJE FUNKCIJE NA KRAJEVIMA OBLASTI DEFINISANOSTI) Ovo je jedna od najznačajnijih tačaka u ispitivanju toka funkcije. Neki profesori zahtevaju da se asimptote rade kao. tačka u
POSLOVNI INFORMACIONI SISTEMI I RA^UNARSKE
 ZNAČAJ RAČUNARSKIH KOMUNIKACIJA U BANKARSKOM POSLOVANJU RAČUNARSKE MREŽE Računarske mreže su nastale kombinacijom računara i telekomunikacija dve tehnologije sa veoma različitom tradicijom i istorijom.
ZNAČAJ RAČUNARSKIH KOMUNIKACIJA U BANKARSKOM POSLOVANJU RAČUNARSKE MREŽE Računarske mreže su nastale kombinacijom računara i telekomunikacija dve tehnologije sa veoma različitom tradicijom i istorijom.
