SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU FAKULTET ELEKTROTEHNIKE, RAČUNARSTVA I INFORMACIJSKIH TEHNOLOGIJA Sveučilišni preddiplomski studij PRI
|
|
|
- Pavlina Simić
- пре 5 година
- Прикази:
Транскрипт
1 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU FAKULTET ELEKTROTEHNIKE, RAČUNARSTVA I INFORMACIJSKIH TEHNOLOGIJA Sveučilišni preddiplomski studij PRIMJENA STROJNOG UČENJA U KLASIFICIRANJU LEGO KOCAKA Završni rad Ervin Hamzić Osijek, 2018.
2 Sadržaj 1. UVOD ZADATAK ZAVRŠNOG RADA TEORIJSKA POZADINA MOTIVACIJA UMJETNE NEURONSKE MREŽE STRUKTURA NEURONSKE MREŽE KONVOLUCIJSKI SLOJ ReLU SLOJ OSTALE AKTIVACIJSKE FUNKCIJE DROPOUT SLOJ I UNAKRSNA VALIDACIJA SLOJ SAŽIMANJA POTPUNO POVEZAN SLOJ TRENIRANJE NEURONSKE MREŽE ALGORITAM PROPAGACIJE POGREŠKE UNATRAG REALIZACIJA NEURONSKE MREŽE PRIPREMA PODATAKA KORIŠTENE TEHNOLOGIJE TENSORFLOW KERAS PRIMJER IMPLEMENTIRANE ARHITEKTURE ZAKLJUČAK...25 LITERATURA...26 SAŽETAK...27 ABSTRACT...28 ŽIVOTOPIS...29
3 1. UVOD U području umjetne inteligencije, posljednjih nekoliko desetljeća donijelo je izniman razvoj metodologija, kao i njihovo usvajanje u primjeni na sve većem broju problema. Na temelju aktualnih trendova, svakako se može reći da se svojevrstan naglasak u okviru umjetne inteligencije kao računarske discipline pomiče u smjeru primjenskog aspekta, što kroz dulje razdoblje nakon početaka razvoja nije bio slučaj, već je ta grana imala prvenstveno akademski predznak. U tom smislu, primjeri poput obrada govora, prepoznavanje ljudskog lica ili pak potpuno ili djelomično autonomne vožnje samo su neki od istaknutih primjera koje pronalazimo u svakodnevnom životu, a koji su zasnovani na pristupima strojnog učenja. Razlog takvim promjenama i napretku leži ponajprije u sve većoj pristupačnosti grafičkih procesorskih jedinica visokih performansi, kao i velikih podatkovnih skupova. Samim time, otvoren je put ka treniranju vrlo složenih neuronskih mreža, što ujedno znači i početak u današnje vrijeme vrlo perspektivne discipline poznate pod nazivom duboko učenje, a to je stvorilo nove potencijale u područjima poput računalnog vida i već spomenute obrade govora, ali i mnogih drugih, odnosno svih onih u kojima se rješavanje problema svodi na svojevrsnu identifikaciju određenog uzorka ili trenda iz velike količine nestrukturiranih podataka. Kao rezultat toga, niz velikih tehnoloških kompanija poput Microsofta, Google-a, YouTube-a ili Amazona provode procese redizajna svojih ključnih proizvoda i usluga imajući u vidu pristupe dubokog učenja. Vrlo sličan trend pojavio se i među vodećim kompanijama iz sektora razvoja i proizvodnje procesorskih jedinica, kao i u okviru FPGA (engl. Field Programmable Gate Array) tehnologije na kojoj se danas zasnivaju računalni sustavi visokih performansi za obradu slike i govora implementirani u velikom broju široko dostupnih elektronskih uređaja, a ponajprije u pametnim telefonima i automobilima. Još jedna vrlo važna domena čiji je razvoj dobio snažan zamah jest autonomna vožnja i različiti sustavi asistencije vozaču (ADAS Advanced Driver Assistance Systems) poput asistencije pri održavanju vozila unutar vozne trake ili pak detekcije objekata u mrtvom kutu, odnosno ispred samog vozila ili npr. sustava za prepoznavanje prometnih znakova. Svi navedeni sustavi danas se baziraju na dubokim neuronskim mrežama radi uspješnosti koju takav pristup pokazuje u rješavanju problema iz područja računalnog vida poput klasifikacije slika te detekcije i lokalizacije objekata, kojem ujedno pripada i zadani problem klasifikacija LEGO kocaka primjenom strojnog učenja. 1.1 ZADATAK ZAVRŠNOG RADA Zadatak ovog rada je primjenom numeričke biblioteke TensorFlow i aplikacijskog sučelja Keras nad prikladnim podatkovnim skupom razviti, istrenirati i testirati duboku konvolucijsku neuronsku mrežu za klasifikaciju slika LEGO kocaka. 1
4 2. TEORIJSKA POZADINA Ovo poglavlje detaljnije obrađuje teorijske pretpostavke i motivaciju koja stoji iza primjene neuronskih mreža na problemima identifikacije objekata gdje ulaznu informaciju predstavlja slika. Naime, ideja o umjetnim neuronskim mrežama nije najnovija matematički modeli kojima ih se može opisati pojavili su se još sredinom prošlog stoljeća. 2.1 MOTIVACIJA Jedan od središnjih zadataka koji se postavlja pri donošenju odluka i predviđanju trendova, a o čemu ovise mnogi važni procesi, kao npr. u poslovnom okruženju ili pak kao u slučaju spomenute problematike koja je obrađena u samom radu prepoznavanje klase objekta bazira se na lokalizaciji i ekstrakciji informacije iz apstraktnog skupa podataka, što je u zadanom problemu slika, a može se raditi i npr. o vremenskom nizu kao informaciji koja ima odgovarajuću interpretaciju poput kretanja cijene određene dionice na tržištu u nekom vremenskom razdoblju. Prije ere strojnog učenja, spomenuti problemi bili su rješivi samo čovjeku na temelju prethodnog iskustva, iako uz određenu (nezanemarivu) vjerojatnost pogreške, ovisno o različitim faktorima. Međutim, ljudski perceptivni sustav vrlo je učinkovit kada govorimo o analizi slike radi prepoznavanja različitih objekata. Točnost koju postiže prosječna osoba u prepoznavanju vizualne informacije u većini je slučajeva svojevrsna referenca koja često još uvijek nije nadmašena metodama strojnog učenja. U tom pogledu, važno je spomenuti ImageNet Large Scale Visual Recognition Challenge (ILSVRC) međunarodno natjecanje i referencu za istraživačke timove u problemima računalnog vida, odnosno prepoznavanja i grupiranja objekata na ImageNet bazi podataka s više od 14 milijuna slika razvrstanih u klase, na kojoj se evaluiraju implementacije rješenja za klasifikaciju. Rezultati postizani iz godine u godinu znakoviti su za primjenu neuronskih mreža u takvim zadacima te predstavljaju važan doprinos i motivaciju daljnjim istraživanjima u tom znanstvenom području godina i rezultati tadašnjeg izdanja natjecanja u kojem je rješenje zasnovano na konvolucijskoj neuronskoj mreži odnijelo uvjerljivu pobjedu (pogreška klasifikacije od 16.4 %, drugoplasirani 26.2 %) smatraju se prekretnicom i početkom revolucije dubokog učenja. Ono što je uslijedilo jest konstantno smanjenje pogreške klasifikacije godine gotovo svi timovi postižu vrijednost pogreške manju od 5 %, što je rezultat vrlo sličan, odnosno bolji od onoga koji se uzima za točnost prepoznavanja koju ostvaruje čovjek na istom skupu podataka (pogreška od približno 5.1 %) [1]. 2
5 Sl. 2.1: Rezultati ImageNet natjecanja u razdoblju od do godine. [3] 2.2 UMJETNE NEURONSKE MREŽE Postavljeni problem zahtijeva da se za određeni podatkovni skup koji se sastoji od niza slika LEGO kocaka osmisli algoritam koji će slike klasificirati prema zajedničkim vizualnim obilježjima. Kao što je već naznačeno, konvolucijska neuronska mreža kao metoda dubokog učenja najefikasniji je, a ujedno i odabrani pristup za rješavanje takvog problema. Klasifikacija slike podrazumijeva da se za određenu sliku kao ulaznu informaciju reproducira klasa kojoj objekt sa slike pripada ili pak niz vjerojatnosti pripadanja najizglednijim klasama. Pod slikom se podrazumijeva JPG slika dimenzija m x n koju možemo predočiti kao niz brojčanih vrijednosti koje povezujemo uz pojedini piksel u slici. Taj je niz veličine m x n x 3, pri čemu se posljednja dimenzija odnosi na RGB vrijednosti. Sve su vrijednosti iz raspona 0 do 255 (oboje uključivo). Tu treću dimenziju u ovom kontekstu često nazivamo dubinom. Ideja o neuronskoj mreži i njezinoj strukturi, barem na apstraktnoj razini, naslanja se način funkcioniranja dijela ljudskog mozga odgovornog za vizualnu percepciju. Ukratko, živčane stanice vizualnog korteksa grupirane su po svojoj funkciji i njihovo okidanje događa se samo u prisustvu određene vrste podražaja, ovisno o grupi [2]. 3
6 Npr. aktivacije se u pojedinoj grupi događaju jedino s obzirom na postojanje okomitih, horizontalnih ili dijagonalnih rubova i sl. Ono što proizlazi iz toga jest da perceptivni sustava čovjeka na svojstven način ''kreće'' od jednostavnih obilježja u analizi vizualnog podražaja te ih grupira i povezuje prema apstraktnijim objektima. Iako se radi o vrlo apstraktnom opisu funkcioniranja, opisani način analize ulazne informacije vrlo je blizak onome kojeg pronalazimo kod neuronskih mreža, što se ogleda i u njihovoj slojevitoj arhitekturi. Intuitivno govoreći, ''provlačenjem'' slike kroz slojeve neuronske mreže, sliku kao ulaz sustava pretačemo u niz vjerojatnosti pripadanja pojedinoj klasi objekata na izlazu. Opisan način funkcioniranja odgovara unaprijednoj neuronskoj mreži (eng. feedforward neural network) čija je implementacija predmet ovog rada. Atribut unaprijedna označava da se informacija unutar neuronske mreže prenosi isključivo u jednom smjeru, bez petlji i povratnih veza kao što je to slučaj kod povratnih neuronskih mreža (eng. recurrent neural network). Sl 2.2: Pojednostavljeni prikaz unaprijedne neuronske mreže [4] 4
7 2.2.1 STRUKTURA NEURONSKE MREŽE Kao što je spomenuto, duboka neuronska mreža inkorporira niz slojeva uvijek se radi o određenom broju konvolucijskih, nelinearnih (ReLU) i sažimajućih (eng. undersampling, pooling layer) slojeva koji su zaključeni jednim ili više potpuno povezanih slojeva. Svi unutarnji slojevi (između prvog konvolucijskog i potpuno povezanog sloja na kraju) nazivaju se i skrivenim slojevima. Slojevi dolaze u određenom slijedu, odnosno grupirani su na odgovarajući način. Značaj i operacije koje podrazumijevamo pod svakim od slojeva bit će pojašnjeni u nastavku. Sl. 2.3: Organizacija slojeva neuronske mreže zajedničko velikoj većini arhitektura je konvolucijski sloj na početku i potpuno povezani sloj kao završni [2] KONVOLUCIJSKI SLOJ Sloj koji se uvijek pojavljuje kao prvi u konvolucijskoj neuronskoj mreži (eng. Convolutional Neural Network CNN) upravo je konvolucijski sloj. Ovdje je potrebno uvesti pojam filtra (također neuron ili jezgra) kao manje strukture (matrice) koja se ''pomiče'' po slici za analizu, odnosno koji je konvoluiran sa slikom prikazanom nizom RGB brojčanih vrijednosti. S apstraktnog stajališta, svrha filtra je identifikacija pojedinih manjih obilježja na slici. Matematički, konvolucija ovdje podrazumijeva niz pojedinačnih operacija množenja elemenata filtra sa spomenutim RGB vrijednostima slike. Uvijek se uzima da konvolucija kreće iz gornjeg lijevog kuta slike. Tada, ako je slika npr. dimenzija 64 x 64, a odabrani filtar 6 x 6, to znači da svaki korak konvolucije imati 108 operacija množenja pojedinačnih elemenata (ne zaboraviti na to da imamo treću dimenziju, dakle potrebno je izvesti 6 * 6 * 3 = 108 operacija). Svi se parcijalni rezultati množenja sumiraju, te se dobiva pojedinačna vrijednost. Filtar se zatim pomiče udesno za određeni broj elemenata (piksela slike) i tako do kraja retka, nakon čega se pozicionira do kraja ulijevo i obično jedno polje niže te se isti postupak ponavlja dok se ne dođe do posljednje pozicije koju filtar takvim pomicanjem može zauzeti nad slikom (filtar u donjem desnom uglu slike). Opisani postupak najslikovitije je predočen na slici 6. Korak pomaka filtra (eng. stride) predstavlja jedan od hiperparametara neuronske mreže i potreban je za određivanje veličine izlazne matrice konvolucijskog sloja [3]. Ta je matrica ujedno i ulaz za idući sloj neuronske mreže te se naziva mapom aktivacija (eng. activation map, feature map). U našem slučaju, s obzirom na spomenute dimenzije filtra i slike, rezultat konvolucije bila bi matrica dimenzija 59 x 59. 5
8 Sl. 2.4: Prikaz operacije konvolucije filtra sa slikom i dobivanja mape aktivacija [2] Kao što je spomenuto, filtar efektivno izolira pojedine strukture unutar slike. U svezi s time, ako se težine filtra poklope s odgovarajućim područjem slike, odgovarajuća vrijednost u mapi aktivacija bit će izrazito velika. Sl. 2.5: Rezultat jednog koraka konvolucije za slučaj velikog poklapanja segmenta slike s koeficijentima filtra [2] Ono što je važno istaknuti jest da se prolaskom filtra po ulaznom volumenu na ovaj način prebrzo gube prostorne dimenzije. U gornjem se primjeru vidi da za ulaz dimenzija 64 x 64 proizlazi mapa veličine 59 x 59. Time bi se prolaskom već kroz nekoliko konvolucijskih slojeva dimenzija izlaznog volumena smanjila na neželjeno male veličine. To posebno negativno utječe na ekstrakciju detalja niske razine u ranijoj fazi treniranja neuronske mreže. Kako bi očuvali prostorne dimenzije, ulazni se volumen proširi poljima koja sadrže nule (eng. zero padding) kako prikazuje slika 7. 6
9 Sl. 2.6: Prelazak filtra po ulaznom uzorku Sl. 2.7: Povećanje dimenzija ulaznog volumena dodavanjem polja s nulama [3] Ovim postupkom uveli smo još jedan hiperparametar neuronske mreže. U konačnici, dimenzija mape aktivacija određuje se prema sljedećem izrazu [3]: O = W K+2P S + 1, (2.1) gdje je O dimenzija ulazne matrice, W je dimenzija mape aktivacija (izlaz konvolucijskog sloja), K je dimenzija filtra, P proširenje nulama (u gornjem primjeru iznosi 2), a S je korak filtra. Jednostavnim računom može se vidjeti da za W = 32, K = 5, P = 2 i S = 1 dimenzija koja je bila prisutna na ulazu ostaje sačuvana. 7
10 ReLU SLOJ Kako bi se moglo razumjeti funkciju koju ReLU (eng. Rectified Linear Unit) sloj ima u neuronskoj mreži, potrebno je uvesti pojam aktivacijske funkcije. Ovdje je zgodno nastaviti spomenutu paralelu između neuronskih mreža i ljudskog perceptivnog sustava. Neuroni u živčanom sustavu preuzimaju signale preko dendrita i generiraju električni potencijal na svom aksonu koji se zatim grana i taj se signal prenosi sinaptičkim vezama na dendrite drugih neurona. Jakost sinaptičke veze određuje faktor pojačavanja ili potiskivanja privedenog signala, što je ključno za interpretaciju podražaja, a ujedno i ekvivalent težinama filtra kojima je modeliran konvolucijski sloj neuronske mreže. Unutar samog neurona događa se, uvjetno rečeno, sumacija doprinosa pojedinih signala koji su stigli preko dendrita živčane stanice. Ukoliko ta suma prekoračuje određeni prag (eng. threshold), događa se aktivacija, okidanje neurona, što rezultira pojavom izrazitog potencijala na aksonu živčane stanice. Procesom učenja kod čovjeka utječe se na jakost sinaptičkih veza. Slično tome, treniranjem neuronske mreže prilagođavaju se vrijednosti koeficijenata filtra. Sl. 2.8: Pojednostavljeni matematički model neurona [5]. Osnovni matematički model neurona bio bi ovakav: 0, w j x j b j y = 1, w j x j > b { j 8
11 Sljedeći je zapis istog izraza međutim učestaliji: 0, w j x j b 0 j y = 1, w j x j b > 0 { j Parametri prikazanog modela su sljedeći: x ulazna veličina, svojstvo (eng. input feature), w težina (eng. weight), b prag (eng. bias). Ulazna veličina u pojednostavljenom slučaju predstavlja binarnu vrijednost (0 ili 1) koja odgovara tome je li neki preduvjet ili događaj ispunjen, težina je faktor koji naznačava relevantnost pojedine ulazne veličine, a bias je efektivno prag okidanja neurona. Predstavljeni model neurona naziva se TLU perceptronom (eng. Threshold Logic Unit). Nažalost, ovakav model pokazuje izrazite nedostatke utoliko što rezultira mrežama koje su vrlo teške za treniranje. Naime, u velikom broju slučajeva, mala promjena jednog od ulaza takvog perceptrona rezultirat će promjenom njegovog izlaza iz 0 u 1 ili obrnuto, što jako utječe na rezultat. Potrebna je drukčija aktivacijska funkcija od opisane. Općenito, aktivacijskom funkcijom ostvarujemo mapiranje izlaza funkcije iz modela neurona f(x) = (w i x i + b i ) (2.2) u određeno područje vrijednosti koje se razlikuje između pojedinih aktivacijskih funkcija. Aktivacijska funkcija za koju smo ustanovili problem zapravo je step funkcija, a da bi taj problem bio izbjegnut, prvenstveno je potrebna ''analogna'' funkcija. ReLU funkcija jedna je od najzastupljenijih i definirana je na sljedeći način: f(x) = max(0, x), (2.3) gdje je x vektor ulaznih vrijednosti neurona. Sl. 2.9: Graf ReLU aktivacijske funkcije [9] 9
12 ReLU je u velikoj većini slučajeva preferirana vrsta aktivacijske funkcije, prvenstveno radi toga što omogućuje bolje performanse neuronske mreže u odnosu na sigmoidnu, odnosno tangens hiperbolnu funkciju [11]. To podrazumijeva bržu konvergenciju težina i pragova vrijednostima koje daju minimalnu pogrešku klasifikacije objekta, što znači da je treniranje mreže time brži proces (budući da je dostizanje globalnog minimuma vrijednosti pogreške i konačan cilj treniranja neuronske mreže). Kao matematička operacija, ReLU je vrlo nezahtjevna funkcija za izvođenje. Također, još jedno od istaknutih svojstava te funkcije jest efikasnost s obzirom na broj okinutih neurona pri obradi pojedinog inputa. Drugim riječima, različiti ulazi (slike) rezultiraju okidanjem različitih (manjih) grupa neurona uz mala preklapanja između grupa. Naime, kao što se vidi iz grafa funkcije, svi neuroni čija je suma po funkciji (2.2) negativna bit će isključeni. Ta separiranost aktivacija donosi bolju sposobnost predikcije utoliko što se smanjuje prenaučenost (eng. overfitting) nad podacima za trening. Prenaučenost ili pretreniranost neuronske mreže karakterističan je problem kod određenih algoritama strojnog učenja, pri čemu je posljedica nedovoljna sposobnost generalizacije od strane istreniranog modela kada taj model izložimo novim podacima, različitim od onih na kojima je model treniran. Sl. 2.10: Pravac dobra generalizacija, krivulja jako loša generalizacija [12] Slika 10 jednostavan je primjer koji prikazuje razliku između ciljane aproksimacije podatkovnog skupa i prenaučenog modela koji na danom skupu čak savršeno oponaša trend, ali kada bi se izvodila ekstrapolacija izvan prikazanog područja, model predstavljen pravcem dao bi puno točnije rezultate. Bolju generalizaciju u pravilu predstavlja što jednostavnija i ''glađa'' krivulja. Općenito govoreći, ono na što prvenstveno ciljamo primjenom aktivacijske funkcije jest da neuronsku mrežu učinimo nelinearnom, što omogućuje da mreža aproksimira nelinearne zakonitosti između ulaza i izlaza s visokom preciznošću. Bez slojeva aktivacijskih funkcija, neuronska bi mreža mogla precizno mapirati samo linearne procese. 10
13 Naime, funkcija f(x) = wx + b kojom je opisan pojedini neuron predstavlja polinom prvog reda, a linearna kombinacija više takvih funkcija ponovno daje polinom prvog reda. Dakle, neovisno o tome koliko bi slojeva neuronska mreža imala, efektivno bi se radilo o mreži sa samo jednim slojem, što je naravno vrlo ograničavajuće. Sl. 2.11: Primjer linearnog klasifikatora [8] Takva bi mreža mogla biti upotrijebljena jedino u slučaju binarne klasifikacije i to kada uzorci u koordinatnoj ravnini imaju takvu distribuciju da ih je moguće razdvojiti povlačenjem pravca. Time bi bio realiziran linearni klasifikator. Problem klasifikacije slike s velikim brojem razreda izrazito je nelinearan pa je primjena (nelinearne) aktivacijske funkcije svakako neizostavna OSTALE AKTIVACIJSKE FUNKCIJE Kako bi se još bolje razumjelo radi čega je ReLU preferirana aktivacijska funkcija, zgodno je dodatno pojasniti svojstva drugih dviju često spominjanih nelinearnih aktivacijskih funkcija sigmoidne i tangens hiperbolne funkcije. Sigmoidna funkcija definirana je na sljedeći način: f(x) = σ(x) = 1 1+e x (2.4) 11
14 Sigmoidnu funkciju možemo promatrati kao ''zaglađenu'' step funkciju, što se na prvi pogled čini kao pogodna karakteristika jer je time prevladan glavni nedostatak step funkcije (binarna aktivacija radi koje je treniranje mreže vrlo zahtjevan proces). Iako je u slučaju sigmoidne funkcije interval aktivacija ograničen između 0 i 1, što je svojevrsna prednost u odnosu na ReLU koja je neograničena u smjeru pozitivnih vrijednosti aktivacija (a jako izrazite aktivacije nisu poželjne), glavni je problem što se za aktivacije bliske 0 i 1 gradijent jako smanjuje, odnosno učenje se jako usporava. Navedeni problem poznat je kao nestajući gradijent (engl. vanishing gradient) To otežava treniranje mreže jer, osim sporosti, posljedica je i ''upadanje'' u lokalne minimume funkcije pogreške predikcije. Sl. 2.12: Zasićenje derivacije sigmoidne funkcije [9] Tangens hiperbolna funkcija je pak samo skalirana sigmoidna funkcija: f(x) = tanh(x) = ex e x = 2 σ(2x) 1 e x + e x Sl. 2.13: Usporedba sigmoidne i tangens hiperbolne aktivacijske funkcije [10] 12
15 Prednost tangens hiperbolne funkcije nad sigmoidnom je prvenstveno izraženiji gradijent u ulaznom intervalu između -1 i 1, što pogoduje brzini treninga, ali se nailazi na isti problem nestajućeg gradijenta izvan tog područja DROPOUT SLOJ I UNAKRSNA PROVJERA Jedan od jednostavnijih postupaka za smanjenje sklonosti mreže da razvije pretreniranost je primjena dropout slojeva u fazi treniranja neuronske mreže, a to donosi nasumično isključivanje određenog broja neurona s obzirom na oba prolaza kroz mrežu (unaprijed i unatrag) kako bi se mrežu učinilo redundantnijom i smanjilo usvajanje svojstava koja predstavljaju šum, kao i suzbilo stvaranje međuovisnosti između pojedinih neurona. S druge strane, primjenom dropout slojeva produljuje se vrijeme koje je mreži potrebno za konvergenciju. Sl. 2.14: Deaktivacija (dropout) pojedinih neurona [11] Često korištena metoda kojom se može ocijeniti sklonost neuronske mreže prenaučenosti jest k-struka unakrsna provjera (eng. k-fold cross validation). Tom se metodom može dati procjena testne pogreške. Sam postupak sastoji se u dijeljenju ukupnog podatkovnog skupa na k podskupova i potom se u svakoj od k iteracija izvodi eksperiment gdje se jedan od tih k podskupova odabere kao testni, a nad preostalih k-1 mreža se trenira. Nakon toga, rezultati iz k eksperimenata se usrednjavaju kako bi se dobila ocjena performansi prediktivnog modela. Na taj se način maksimiziraju dostupni podaci u odnosu na standardnu statičku podjelu podataka na podskup za trening i validaciju. Naime, svaki se podatak iskoristi i za učenje i za evaluaciju modela, no to se učini samo jednom za svaki od uzoraka. 13
16 Metoda se uglavnom koristi na manjim podatkovnim skupovima kada podataka nema dovoljno da bi se skup podijelio na isključive podskupove za učenje i validaciju kao u uobičajenim slučajevima. Ukupan podatkovni skup najčešće se pritom dijeli na 10 podgrupa (k = 10). Značajno je i to da je sam postupak skup za veliku vrijednost parametra k radi toga što metoda zahtijeva k treniranja modela SLOJ SAŽIMANJA U okviru sloja sažimanja (eng. pooling layer), manji segmenti mape aktivacija proizašle iz prethodnog konvolucijskog sloja svode se na pojedinačne elemente, što rezultira smanjenjem dimenzija mape, a to pak povlači manji broj potrebnih računskih operacija u kasnijim slojevima. Također, tim se postupkom povećava prostorna neosjetljivost neuronske mreže (neosjetljivost s obzirom na prostorne pomake objekata unutar uzorka). Sloj sažimanja pritom se može realizirati na različite načine. Najčešće korišteno je sažimanje usrednjavanjem gdje se pojedinačna vrijednost nad malim segmentom volumena izvede kao aritmetička sredina grupiranih elemenata ili se pak uzme maksimalna vrijednost među elementima (eng. max pooling). Na donjem primjeru radi se o sažimanju maksimalnom vrijednošću gdje je polje nad kojim se sažimanje radi dimenzija 2 x 2, te je izlazna mapa značajki 4 puta manja (faktor skaliranja jednak je 2). Ono u čemu se ove dvije metode sažimanja također razlikuju jest to što je kod sažimanja maksimalnom vrijednošću potrebno memorirati lokaciju elemenata s maksimalnim vrijednostima (onih koji su izvučeni iz podsegmenata), dok kod sažimanja srednjom vrijednošću to nije slučaj. Sl. 2.15: Postupak sažimanja maksimalnom vrijednošću [2] 14
17 POTPUNO POVEZAN SLOJ Potpuno povezan sloj (eng. fully connected layer) uvijek dolazi na kraju mreže kao posljednji sloj. Nakon što je stvoren prostor značajki (eng. feature space) prolaskom ulaznog volumena kroz sve prethodeće slojeve, taj završni sloj ima ulogu konačne klasifikacije ulazne slike te kao izlaz daje vektor duljine N, gdje je N broj klasa objekata definiranih u podatkovnom skupu. Pojedina vrijednost unutar vektora predstavlja vjerojatnost da za ulazni volumen pripada odgovarajućoj klasi od tih N klasa. Primjerice, za N = 10, gdje se radi o problemu prepoznavanja pojedine znamenke, gdje je izlazni vektor [ ], najveća je vjerojatnost da se na ulazu pojavila znamenka 4 i ona iznosi 80%. 2.3 TRENIRANJE NEURONSKE MREŽE Kao što je već naznačeno, proces učenja neuronske mreže nad određenim podatkovnim skupom podrazumijeva konstantna ažuriranja vrijednosti težina te mreže. Ta podešavanja težinskih faktora vode ka smanjenju greške klasifikacije na minimum. Težine filtra prije samog učenja imaju slučajne vrijednosti koje ni na koji način nisu uvjetovane podatkovnim skupom za učenje ili validaciju. Slično kao što čovjek u najranijoj dobi upoznaje okolinu oko sebe povezujući određeni naziv predmeta s njegovom vizualnom pojavom, tako i neuronska mreža uči parametre prolaskom kroz veliku količinu slikovnih podataka uparenih s odgovarajućim nazivom klase. Spomenuta metoda spada u klasu metoda nadziranog učenja (eng. supervised learning). Algoritam čija je uporaba najraširenija za treniranje neuronskih mreža i općenito najpopularniji za nadzirano učenje kod višeslojnih perceptrona naziva se algoritmom propagacije pogreške unatrag (eng. error backpropagation). Glavni razlog radi kojeg je algoritam toliko zastupljen je što se njime postiže najbrži spust u prostoru težina. Algoritam je detaljnije opisan u nastavku ALGORITAM PROPAGACIJE POGREŠKE UNATRAG Algoritam propagacije pogreške unatrag ima četiri karakteristične faze unaprijedna faza (eng. forward pass), izračun pogreške, unazadna faza (eng. backward pass) i ažuriranje težina. Vratimo li se na spomenuti primjer s klasifikacijom znamenki, mreža na samom početku neće davati izrazitu preferenciju bilo kojoj klasi (znamenki), što znači da će izlazni vektor vjerojatnosti imati ujednačene vrijednosti, dok će ciljani rezultat imati vjerojatnosti jednake nuli za sve znamenke osim one koja se pojavila na ulazu. Radi toga pogreška u početnoj fazi treniranja ima veliku vrijednost. 15
18 Jedan od češće korištenih načina za određivanje pogreške jest prema srednjem kvadratnom odstupanju (eng. mean square error): E total = 1 n (x i,target x i,output ) 2 i (2.5) U spomenutom primjeru klasifikacije znamenki, vektori xtarget i xoutput bi na početku faze učenja mogli izgledati ovako (znamenka na ulazu je 5): xtarget = [ ], xoutput = [ ]. Dakle, ovaj se optimizacijski problem sastoji u pronalasku minimuma pogreške između predikcije koju radi neuronska mreža i ciljane vrijednosti s obzirom na težinske faktore. Prve dvije od spomenutih faza obavljene su prolaskom slike kroz mrežu i određivanjem pogreške nastale pogreške u predikciji prema izrazu (2.5), nakon čega slijedi ključan korak, a taj korak podrazumijeva propagaciju izračunate pogreške u obrnutom smjeru (prema prvom sloju) i određivanje gradijenta pogreške. Gradijent pogreške, odnosno parcijalne derivacije pogreške po težinama unutar slojeva neuronske mreže, govori koliko se intenzivno mijenja vrijednost pogreške s obzirom na težine, a određuje se kako bi se znalo na koji način podesiti težine da bi se greška postupno odvela u minimum. Korekcija težine pritom se odvija u pravcu negativnog gradijenta [7]. Sada uzmimo sljedeći primjer mreže kako je prikazano: 16
19 Sloj s neuronom j uzimamo kao izlazni te gledano iz tog sloja počinje određivanje pogreške rekurzivnim računanjem za svaki neuron pojedinačno sloj po sloj. Težinski faktori veza između neurona j i onih iz prethodnog sloja označeni su s wji. Ulaz bloka aktivacijske funkcije označen s vj jednak je: (2.6) pri čemu yi predstavlja izlaz i-tog neurona prethodnog sloja. Zatim imamo konačni izlaz yj neurona nakon aktivacijskog bloka: gdje aktivacijska funkcija djeluje na izlaz neurona vj. (2.7) Gradijent se potom računa na sljedeći način: (2.8) Kada se gradijent odredi, sljedeći korak je konačno ažuriranje težina, što je općenito dano sljedećim izrazom (metoda najbržeg spusta): w ji = w ji-1 η* de (2.9) dw ji 1 Parametar η predstavlja brzinu učenja (eng. learning rate) i radi se o veličini koju sami određujemo. 17
20 Veća vrijednost znači bržu konvergenciju težinskih faktora prema vrijednosti minimuma pogreške (dakle postupak treniranja neuronske mreže kraće traje), no to ujedno znači veću nestabilnost i može značiti da točka minimuma nikada neće biti dosegnuta zbog prevelikih skokova [2]. Međutim, nestabilniji proces učenja ima jednu karakterističnu prednost, a to je da je takav proces manje sklon upadanju u lokalne minimume gdje bi se onda završilo treniranje bez da je pronađen stvarni minimum pogreške. Sl. 2.16: Problem previsoke brzine učenja [1] 18
21 3. REALIZACIJA NEURONSKE MREŽE 3.1 PRIPREMA PODATAKA Kao što je već naznačeno, konvolucijske neuronske mreže zahtijevaju velike količine podataka ako se računa na imalo reprezentativne rezultate. Pod reprezentativnim rezultatom smatra se točnost predikcije od strane istreniranog modela nad novim podacima iskazana kao udio ispravno prepoznatih uzoraka. Veličina tog udjela naravno ovisi o vrsti uzoraka i klasifikacije koja se izvodi. U principu je poželjno raspolagati skupom reda veličine tisuću ili deset tisuća uzoraka po klasi. Te su količine podataka potrebne jer je postupak ekstrakcije svojstava i struktura iz podataka spor, a posebno je to istaknuto kod visoko dimenzionalnih ulaznih uzoraka kao što su slikovni podaci. Klasifikacija slika u pravilu zahtijeva kompleksne modele s velikim brojem parametara, no da bi razvoj tako kompleksnih modela imao smisla, ključno je raspolagati izrazito velikim podatakovnim skupom jer je uspješnost optimizacije parametara mreže proporcionalna broju iteracija u procesu treniranja mreže. Tako na primjer jedna od poznatijih dubokih neuronskih mreža za klasifikaciju slika VGGNet (pobjednik natjecanja ILSVRC godine) ima 140 milijuna parametara. Može se reći kako je, barem u većini slučajeva, sinteza kvalitetnog podatkovnog skupa na kojem će neuronska mreža trenirati veći i prioritetniji zadatak od samog dizajna mreže. Međutim, u nekim slučajevima dovoljno veliki podatkovni skupovi nisu izvorno dostupni ili bi izgradnja takvog skupa ''ručnim'' metodama bila predugotrajan postupak. Ručni postupak podrazumijevao bi npr. ručno (pojedinačno) uzimanje novih slika, te pridruživanje oznake klase svakoj slici. Radi toga se vrlo često nad slikama primjenjuju određene transformacije kako bi se uvećala izvorna količina podataka (engl. data augmentation) [16]. Pritom se može raditi o vrlo raznolikim metodama u ovisnosti o tome s kakvim podacima se radi, no za slikovne podatke karakteristične su afine transformacije poput skaliranja, rotacije ili smika (engl. shearing). Sl.3.1: Afine transformacije (engl. affine transformation) [14] 19
22 Sl. 3.2: Primjer transformacija nad izvornom slikom [15] Pored spomenutih metoda, nad slikovnim se podacima često primjenjuju i modifikacije parametara poput osvjetljenja ili pak dodavanje šuma. Osim samog povećanja podatkovnog volumena, dodatna prednost koja se ostvaruje primjenom transformacijskih postupaka na izvornim podacima jest to da model treniran na takvom podatkovnom skupu postaje neosjetljiviji upravo na spomenute varijacije, što je u realnim uvjetima vrlo poželjno svojstvo modela. Može se reći da su na taj način uklonjene irelevantne karakteristike iz podataka. Naime, kada je cilj ispravna klasifikacija slike, na samu klasifikaciju ne bi trebao utjecati npr. položaj ili orijentacija objekta unutar slike. Osim toga, na taj se način ujedno i smanjuje sklonost modela razvijanju problema pretreniranosti, odnosno takav model ima veću sposobnost generalizacije. Kao što se može i pretpostaviti, upravo su modeli trenirani na malim podatkovim skupovima loši u pogledu generalizacije. U konačnici, ono što model čini kvalitetnim, a što proizlazi iz podatkovnog skupa na kojem je treniran jest balans u pogledu količine i relevantnosti karakteristika ekstrahiranih iz podataka. 3.2 KORIŠTENE TEHNOLOGIJE TENSORFLOW TensorFlow je biblioteka otvorenog koda (engl. open source) namijenjena za numeričke proračune izvorno razvijena od strane Google Brain istraživačkog tima za potrebe internih projekata. Jedna od istaknutih primjena ovog frameworka upravo je u području strojnog učenja, a posebno se to odnosi na duboko učenje. Karakteristika ove biblioteke je i mogućnost razvoja na različitim platformama, što podrazumijeva opciju iskorištenja grafičke procesorske jedinice, a to je od velikog značaja budući da su višeslojne neuronske mreže i treniranje pripadajućih modela računski vrlo zahtjevni pa je time vrijeme razvoja znatno skraćeno. Jezgru računskog modela oko kojeg je TensorFlow baziran čini struktura koja se naziva tenzor. 20
23 Ostavljajući po strani stroge matematičke definicije, može se reći da je tenzor višedimenzionalno polje podataka nad kojim su definirana određena transformacijska svojstva. Ta svojstva opisuju promjene spomenutog polja kao rezultat matričnih operacija. Modeliranje neuronske mreže primjenom TensorFlow-a podrazumijeva definiranje instance dataflow grafa kojeg čini niz objekata koji predstavljaju jedinice izračuna (engl. units of computation). TensorFlow grafovi prevode se u visoko optimiziran C++ programski kod. U radu se TensorFlow ne koristi izravno već se pozivi njegovih konstrukata ostvaruju kroz Keras sučelje KERAS Keras je aplikacijsko programsko sučelje (engl. application programming interface) visoke razine pisano u programskom jeziku Python, a omogućuje definiciju i treniranje kompleksnih neuronskih mreža te funkcionira kao sloj iznad TensorFlow-a [17]. Keras ima važnu primjenu u području dubokog učenja jer je njime ostvariv jednostavniji dizajn neuronske mreže gdje je fokus izravno na realizaciji apstraktnih struktura koje su predstavljene u teorijskom dijelu o konvolucijskim neuronskim mrežama (slojevi, aktivacijske funkcije, itd.). Dakle, sam proces dizajna je time intuitivniji i brži, a programer na raspolaganju ima velik broj pripremljenih implementacija spomenutih elemenata mreže. 3.3 PRIMJER IMPLEMENTIRANE ARHITEKTURE U ovom će dijelu biti izneseni detalji arhitekture i parametara konvolucijske neuronske mreže realizirane spomenutim tehnologijama. Za treniranje i validaciju mreže korišten je relativno mali podatkovni skup podijeljen na 11 klasa s približno 200 do 250 uzoraka po klasi. Validacijski skup sastoji se od ukupno 200 slika. Budući da se radi o ograničenom skupu podataka, nad skupom su primijenjena 4 tipa transformacija skaliranje slike, uvećanje (engl. zoom), zrcaljenje slike po horizontalnoj osi i smik, čime je izvorni podatkovni volumen upeterostručen. Slike su izvorno velikih dimenzija (640x480), te im je prije bilo kakve obrade i treniranja mreže smanjena veličina na dimenzije 64 x 48. Što se tiče arhitekture same mreže, u početku je odabrana relativno jednostavna izvedba s tri povezane kombinacije konvolucijskog i sloja sažimanja maksimalnom vrijednošću nakon kojeg dolazi aktivacijska funkcija, a potom dolazi potpuno povezan sloj. Konvolucijski slojevi imaju po 32 filtra dimenzija 3 x 3, sažimanje se izvodi po blokovima veličine 2 x 2, te se koristi ReLU aktivacijska funkcija. 21
24 Sl. 3.3: Uzorci skupa za treniranje mreže iz 11 klasa Za prvu iteraciju treniranja mreže, evaluacija točnosti klasifikacije odvija se nakon obrade svakih 10 ulaznih uzoraka (engl. batch), te se izvodi 10 epoha treniranja, odnosno mreža se 10 puta trenira na ukupnom podatkovnom skupu za učenje. Od ostalih hiperparametara, korak pomaka filtra (engl. stride) iznosi 1, te se ne primjenjuje proširenje ulaznog volumena dodatnim poljima s nulama (engl. zero padding). Takvom je mrežom u prvoj trening iteraciji (testni slučaj 1) postignuta točnost klasifikacije (engl. accuracy) od 65,44 %. Vrijeme treniranja mreže po epohi iznosi nešto više od 1 minute. U idućem eksperimentu, mreža je učinjena nešto kompleksnijom povećanjem broja filtara u konvolucijskim slojevima (testni slučaj 2) na 64. Rezultat je iznosio 69,02 %. Ovo povećanje kompleksnosti gotovo uopće nije usporilo treniranje mreže. Zatim je isproban utjecaj broja epoha treniranja iste mreže. Povećanjem broja epoha na 20, dobiva se točnost od 79,23 % u 19. epohi, no nakon obavljenih 20 epoha, točnost počinje opadati (testni slučaj 3). Daljnjim eksperimentima u pravcu povećanja kompleksnosti početne mreže, isprobano je dodavanje još dviju spomenutih kombinacija skrivenih slojeva (konvolucijski sloj sloj sažimanja ReLU; testni slučaj 4) u odnosu na testni slučaj 2 te je zabilježena točnost klasifikacije od 71,10 %, a potom je i uvećan broj filtara konvolucijskog sloja na 128 (testni slučaj 5) uz rezultat od 74,69 %. Oba rezultata odnose se na treniranje kroz 10 epoha. Vrijeme treniranja mreže povećalo se time za približno 50 % u odnosu na prve dvije implementacije. Kao posljednji primjer, mreža iz posljednjeg testnog slučaja trenirana je kroz 20 epoha (testni slučaj 6). Tim je eksperimentom u posljednjoj epohi dobivena točnost od 83,17 % U konačnici, primjetno je da kompleksnija mreža ima veći potencijal za učenje parametara nelinearnog procesa nad ovakvim podatkovnim skupom, što je i očekivano. 22
25 Sl. 3.4: Početno odabrana arhitektura mreže za klasifikaciju slika LEGO kocaka (prikazano radi jednostavnosti isprobani kompleksniji testni primjeri s više slojeva donosili su samo dodatne blokove konvolucija sažimanje ReLU) testni slučaj Broj testnog slučaja Broj kombinacija skrivenih slojeva Broj filtara konvolucijskog sloja Broj epoha Točnost klasifikacije - trening [%] Točnost klasifikacijevalidacija [%] (konvolucija - sažimanje ReLU) ,44 57, ,02 60, ,23 68, ,10 64, ,69 69, ,17 74,26 Tablica 3.1: Obrađeni testni slučajevi treniranja mreže i dobiveni rezultati 23
26 Sl. 3.5: Usporedba procesa učenja mreže na dva najuspješnija testna slučaja Konačno, postupkom validacije se istrenirane mreže testiraju na podatkovnom skupu koji je obično nešto različit od testnog jer se na taj način provjerava najvažnija sposobnost neuronske mreže, a to je sposobnost generalizacije. Budući da je izvorni podatkovni skup u ovom slučaju relativno ujednačen po svojim karakteristikama, odnosno same slike se ne razlikuju u znatnoj mjeri s obzirom na svojstva kao što su osvjetljenje, pozadina, položaj objekta na slici i sl., da bi se testirala generalizacijska svojstva istrenirane mreže, korištene su nešto različite postavke transformacija nad podskupom za trening i onim za validaciju. U konačnici, najbolji validacijski rezultat postignut je u testnom slučaju 6 kao što je i očekivano te iznosi 74,26 %. Primjetna su znatnija odstupanja točnosti prilikom validacije u odnosu na točnost postizanu u toku treninga, što se u najvećoj mjeri pripisuje ipak nedovoljno velikom podatkovnom skupu. 24
27 ZAKLJUČAK Radom su razjašnjene teorijske pretpostavke koje stoje iza primjene konvolucijskih neuronskih mreža na problemima klasifikacije slikovnih podataka. Pritom su obrađene sve značajnije specifičnosti dizajna duboke neuronske mreže, u prvom redu uloge pojedinih slojeva i način funkcioniranja algoritma propagacije pogreške unatrag kojim se ažuriraju težinski faktori filtara tijekom treniranja mreže. Također, pokriven je i problem pripreme podataka za treniranje mreže, što je vrlo značajno za uspješnost mreže u klasifikaciji podataka. Cilj rada bio je dizajn i učenje mreže za klasifikaciju slika LEGO kocaka. U izradi rješenja korištena je numerička biblioteka TensorFlow u kombinaciji s aplikacijskim sučeljem Keras. Također, korišten je jedan od već dostupnih podatkovnih skupova koji se sastoji od 11 klasa LEGO kocaka sa po otprilike 200 uzoraka slika po klasi nad kojima je zatim primijenjen niz afinih transformacija radi uvećanja samog skupa i postizanja boljih rezultata klasifikacije. Sama implementacija i treniranje mreže obavljeno je kroz 6 testnih slučajeva gdje je najbolji rezultat klasifikacije iznosio 83,17 %, a validacije 74,26 %. U daljnjem radu fokus bi bio prvenstveno na podatkovnom skupu budući da se taj element pokazao najzahtjevnijim na zadanom problemu. S obzirom da se radi o klasifikaciji LEGO kocaka gdje je prisutan vrlo veliki broj različitih klasa kocaka, a reprezentativne količine podataka nisu lako dostupne, sinteza bogatijeg podatkovnog skupa doprinijela bi kvaliteti procesa treniranja mreže. Nadalje, preporučuje se mrežu trenirati na modificiranoj arhitekturi, s drukčijim hiperparametrima i aktivacijskim funkcijama, a ujedno i primijeniti neke dodatne tehnike transformacije izvornog skupa podataka. 25
28 LITERATURA [1] [2] Understanding-Convolutional-Neural-Networks/ [3] Convolutional-Neural-Networks-Part-2/ [4] [5] [6] [7] [8] [9] _tensor_flow.ipynb [10] 1cbd9f8d91d6?gi=df368c769b68 [11] -less-to-learn-better-dropout-in-deep-machine-learning-74334da4bfc5 [12] =MachineLearning&doc=exercises/ex7/ex7.html [13] [14] [15] [16] [17] [18] -data-part-2-data-augmentation-c26971dc8ced [19] 26
29 SAŽETAK Rad donosi teorijsku pozadinu potrebnu za razumijevanje funkcioniranja i realizacije konvolucijskih neuronskih mreža, danas najzastupljenije metode dubokog učenja na problemima klasifikacije slikovnih podataka. Cilj rada bio je demonstrirati izradu konvolucijske neuronske mreže za rješavanje problema klasifikacije slika LEGO kocaka. U rješavanju zadatka korištene su tehnologije TensorFlow i Keras pomoću kojih je neuronska mreža dizajnirana, trenirana i evaluirana. Na samom kraju rada opisani dobiveni rezultati i zaključci. Ključne riječi: duboko učenje, umjetne neuronske mreže, konvolucijske neuronske mreže, klasifikacija slika, algoritam propagacije pogreške unatrag 27
30 ABSTRACT Title: The application of machine learning for LEGO brick classification This work presents the theoretical background required in order to understand the way of functioning and implementation of convolutional neural networks which are the most widely used method of deep learning applied for image classification problems nowadays. The aim of this work was to demonstrate the design of a convolutional neural network applied on a LEGO brick image classification problem. TensorFlow and Keras were the technologies used in solving this task and by means of which the neural network was designed, trained and evaluated. The results and conclusions are described in the final part of the work. Keywords: deep learning, artificial neural networks, convolutional neural networks, image classification, backpropagation algorithm 28
31 ŽIVOTOPIS Ervin Hamzić rođen je 23. veljače godine u Zagrebu gdje je pohađao osnovnu i srednju školu (Prva gimnazija Zagreb). Po završetku gimnazije upisuje preddiplomski studij elektrotehnike na Fakultetu elektrotehnike i računarstva u Zagrebu godine. Studij od godine nastavlja na Fakultetu elektrotehnike, računarstva i informacijskih tehnologija u Osijeku, smjer Komunikacije i informatika. Trenutno je student 3. godine godine na prvom izdanju natjecanja STEM Games za studente osvaja 4. mjesto u finalu Technology arene. Aktivno se služi engleskim i njemačkim jezikom u govoru i pismu. Ervin Hamzić 29
Klasifikacija slika kucnih brojeva dubokim konvolucijskim modelima
 Klasifikacija slika kućnih brojeva dubokim konvolucijskim modelima Ivan Šego 4. srpnja 2018. Sadržaj 1 Uvod 2 Konvolucijske neuronske mreže Konvolucijski sloj Sloj sažimanja Potpuno povezani sloj 3 Ispitni
Klasifikacija slika kućnih brojeva dubokim konvolucijskim modelima Ivan Šego 4. srpnja 2018. Sadržaj 1 Uvod 2 Konvolucijske neuronske mreže Konvolucijski sloj Sloj sažimanja Potpuno povezani sloj 3 Ispitni
MAZALICA DUŠKA.pdf
 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ELEKTROTEHNIČKI FAKULTET Sveučilišni studij OPTIMIRANJE INTEGRACIJE MALIH ELEKTRANA U DISTRIBUCIJSKU MREŽU Diplomski rad Duška Mazalica Osijek, 2014. SADRŽAJ
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ELEKTROTEHNIČKI FAKULTET Sveučilišni studij OPTIMIRANJE INTEGRACIJE MALIH ELEKTRANA U DISTRIBUCIJSKU MREŽU Diplomski rad Duška Mazalica Osijek, 2014. SADRŽAJ
Microsoft Word - predavanje8
 DERIVACIJA KOMPOZICIJE FUNKCIJA Ponekad je potrebno derivirati funkcije koje nisu jednostavne (složene su). Na primjer, funkcija sin2 je kompozicija funkcija sin (vanjska funkcija) i 2 (unutarnja funkcija).
DERIVACIJA KOMPOZICIJE FUNKCIJA Ponekad je potrebno derivirati funkcije koje nisu jednostavne (složene su). Na primjer, funkcija sin2 je kompozicija funkcija sin (vanjska funkcija) i 2 (unutarnja funkcija).
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br Autonomno kretanje virtualnih objekata Marin Hrkec Zagreb, lipanj 201
 SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br. 6404 Autonomno kretanje virtualnih objekata Marin Hrkec Zagreb, lipanj 2019. iii SADRŽAJ 1. Uvod 1 2. Korišteni alati i tehnologije
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br. 6404 Autonomno kretanje virtualnih objekata Marin Hrkec Zagreb, lipanj 2019. iii SADRŽAJ 1. Uvod 1 2. Korišteni alati i tehnologije
Postojanost boja
 Korištenje distribucije osvjetljenja za ostvaranje brzih i točnih metode za postojanost boja Nikola Banić 26. rujna 2014. Sadržaj Postojanost boja Ubrzavanje lokalnog podešavanja boja Distribucija najčešćih
Korištenje distribucije osvjetljenja za ostvaranje brzih i točnih metode za postojanost boja Nikola Banić 26. rujna 2014. Sadržaj Postojanost boja Ubrzavanje lokalnog podešavanja boja Distribucija najčešćih
Microsoft Word - III godina - EA - Metodi vjestacke inteligencije
 Школска година 2018/2019. Предмет Методи вјештачке интелигенције Шифра предмета 2284 Студијски програм Електроенергетика и аутоматика Циклус студија Година студија Семестар Број студената Број група за
Школска година 2018/2019. Предмет Методи вјештачке интелигенције Шифра предмета 2284 Студијски програм Електроенергетика и аутоматика Циклус студија Година студија Семестар Број студената Број група за
Microsoft Word - 15ms261
 Zadatak 6 (Mirko, elektrotehnička škola) Rješenje 6 Odredite sup S, inf S, ma S i min S u skupu R ako je S = { R } a b = a a b + b a b, c < 0 a c b c. ( ), : 5. Skratiti razlomak znači brojnik i nazivnik
Zadatak 6 (Mirko, elektrotehnička škola) Rješenje 6 Odredite sup S, inf S, ma S i min S u skupu R ako je S = { R } a b = a a b + b a b, c < 0 a c b c. ( ), : 5. Skratiti razlomak znači brojnik i nazivnik
Newtonova metoda za rješavanje nelinearne jednadžbe f(x)=0
 za rješavanje nelinearne jednadžbe f (x) = 0 Ime Prezime 1, Ime Prezime 2 Odjel za matematiku Sveučilište u Osijeku Seminarski rad iz Matematičkog praktikuma Ime Prezime 1, Ime Prezime 2 za rješavanje
za rješavanje nelinearne jednadžbe f (x) = 0 Ime Prezime 1, Ime Prezime 2 Odjel za matematiku Sveučilište u Osijeku Seminarski rad iz Matematičkog praktikuma Ime Prezime 1, Ime Prezime 2 za rješavanje
Microsoft Word - 6ms001
 Zadatak 001 (Anela, ekonomska škola) Riješi sustav jednadžbi: 5 z = 0 + + z = 14 4 + + z = 16 Rješenje 001 Sustav rješavamo Gaussovom metodom eliminacije (isključivanja). Gaussova metoda provodi se pomoću
Zadatak 001 (Anela, ekonomska škola) Riješi sustav jednadžbi: 5 z = 0 + + z = 14 4 + + z = 16 Rješenje 001 Sustav rješavamo Gaussovom metodom eliminacije (isključivanja). Gaussova metoda provodi se pomoću
Uvod u statistiku
 Uvod u statistiku Osnovni pojmovi Statistika nauka o podacima Uključuje prikupljanje, klasifikaciju, prikaz, obradu i interpretaciju podataka Staistička jedinica objekat kome se mjeri neko svojstvo. Svi
Uvod u statistiku Osnovni pojmovi Statistika nauka o podacima Uključuje prikupljanje, klasifikaciju, prikaz, obradu i interpretaciju podataka Staistička jedinica objekat kome se mjeri neko svojstvo. Svi
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br Klasifikacija slika kućnih brojeva dubokim konvolucijskim modelima Iv
 SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br. 5702 Klasifikacija slika kućnih brojeva dubokim konvolucijskim modelima Ivan Šego Zagreb, srpanj 2018. Umjesto ove stranice umetnite
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br. 5702 Klasifikacija slika kućnih brojeva dubokim konvolucijskim modelima Ivan Šego Zagreb, srpanj 2018. Umjesto ove stranice umetnite
(Microsoft Word - Dr\236avna matura - studeni osnovna razina - rje\232enja)
 1. C. Imamo redom: I. ZADATCI VIŠESTRUKOGA IZBORA 9 + 7 6 9 + 4 51 = = = 5.1 18 4 18 8 10. B. Pomoću kalkulatora nalazimo 10 1.5 = 63.45553. Četvrta decimala je očito jednaka 5, pa se zaokruživanje vrši
1. C. Imamo redom: I. ZADATCI VIŠESTRUKOGA IZBORA 9 + 7 6 9 + 4 51 = = = 5.1 18 4 18 8 10. B. Pomoću kalkulatora nalazimo 10 1.5 = 63.45553. Četvrta decimala je očito jednaka 5, pa se zaokruživanje vrši
Matrice. Algebarske operacije s matricama. - Predavanje I
 Matrice.. Predavanje I Ines Radošević inesr@math.uniri.hr Odjel za matematiku Sveučilišta u Rijeci Matrice... Matrice... Podsjeti se... skup, element skupa,..., matematička logika skupovi brojeva N,...,
Matrice.. Predavanje I Ines Radošević inesr@math.uniri.hr Odjel za matematiku Sveučilišta u Rijeci Matrice... Matrice... Podsjeti se... skup, element skupa,..., matematička logika skupovi brojeva N,...,
Numeričke metode u fizici 1, Projektni zadataci 2018./ Za sustav običnih diferencijalnih jednadžbi, koje opisuju kretanje populacije dviju vrs
 Numeričke metode u fizici, Projektni zadataci 8./9.. Za sustav običnih diferencijalnih jednadžbi, koje opisuju kretanje populacije dviju vrsta životinja koje se nadmeću za istu hranu, dx ( dt = x x ) xy
Numeričke metode u fizici, Projektni zadataci 8./9.. Za sustav običnih diferencijalnih jednadžbi, koje opisuju kretanje populacije dviju vrsta životinja koje se nadmeću za istu hranu, dx ( dt = x x ) xy
Raspoznavanje prometnih znakova
 1.7.2013. RASPOZNAVANJE PROMETNIH ZNAKOVA Ivan Filković Mentor: Prof. dr. sc. Zoran Kalafatić 1.7.2013. 2 Sadržaj Motivacija, uvod Sustav za raspoznavanje prometnih znakova Skupovi podataka Rezultati testiranja
1.7.2013. RASPOZNAVANJE PROMETNIH ZNAKOVA Ivan Filković Mentor: Prof. dr. sc. Zoran Kalafatić 1.7.2013. 2 Sadržaj Motivacija, uvod Sustav za raspoznavanje prometnih znakova Skupovi podataka Rezultati testiranja
Metode za automatsko podešavanje boje i svjetline slike
 Metode za automatsko podešavanje boje i svjetline slike Mentor: prof. dr. sc. Sven Lončarić Student: Nikola Banić Zagreb, 9. srpnja 2013. Sadržaj Uvod Boje Postojanost boja Algoritmi za podešavanje boja
Metode za automatsko podešavanje boje i svjetline slike Mentor: prof. dr. sc. Sven Lončarić Student: Nikola Banić Zagreb, 9. srpnja 2013. Sadržaj Uvod Boje Postojanost boja Algoritmi za podešavanje boja
ALIP1_udzb_2019.indb
 Razmislimo Kako u memoriji računala prikazujemo tekst, brojeve, slike? Gdje se spremaju svi ti podatci? Kako uopće izgleda memorija računala i koji ju elektronički sklopovi čine? Kako biste znali odgovoriti
Razmislimo Kako u memoriji računala prikazujemo tekst, brojeve, slike? Gdje se spremaju svi ti podatci? Kako uopće izgleda memorija računala i koji ju elektronički sklopovi čine? Kako biste znali odgovoriti
Sadržaj 1 Diskretan slučajan vektor Definicija slučajnog vektora Diskretan slučajan vektor
 Sadržaj Diskretan slučajan vektor Definicija slučajnog vektora 2 Diskretan slučajan vektor Funkcija distribucije slučajnog vektora 2 4 Nezavisnost slučajnih vektora 2 5 Očekivanje slučajnog vektora 6 Kovarijanca
Sadržaj Diskretan slučajan vektor Definicija slučajnog vektora 2 Diskretan slučajan vektor Funkcija distribucije slučajnog vektora 2 4 Nezavisnost slučajnih vektora 2 5 Očekivanje slučajnog vektora 6 Kovarijanca
Objektno orjentirano programiranje 2P
 Sveučilište u Rijeci ODJEL ZA INFORMATIKU Akademska 2016./2017. godina OBJEKTNO ORIJENTIRANO PROGRAMIRANJE Studij: Preddiplomski studij informatike (dvopredmetni) Godina i semestar: 2. godina, 3. semestar
Sveučilište u Rijeci ODJEL ZA INFORMATIKU Akademska 2016./2017. godina OBJEKTNO ORIJENTIRANO PROGRAMIRANJE Studij: Preddiplomski studij informatike (dvopredmetni) Godina i semestar: 2. godina, 3. semestar
Grupiranje podataka: pristupi, metode i primjene, ljetni semestar 2013./ Standardizacija podataka Predavanja i vježbe 8 Ako su podaci zadani
 Grupiranje podataka: pristupi, metode i primjene, ljetni semestar 2013/2014 1 5 Standardizacija podataka Predavanja i vježbe 8 Ako su podaci zadani s više obilježja (atributa), ta se obilježja mogu međusobno
Grupiranje podataka: pristupi, metode i primjene, ljetni semestar 2013/2014 1 5 Standardizacija podataka Predavanja i vježbe 8 Ako su podaci zadani s više obilježja (atributa), ta se obilježja mogu međusobno
Stručno usavršavanje
 TOPLINSKI MOSTOVI IZRAČUN PO HRN EN ISO 14683 U organizaciji: TEHNIČKI PROPIS O RACIONALNOJ UPORABI ENERGIJE I TOPLINSKOJ ZAŠTITI U ZGRADAMA (NN 128/15, 70/18, 73/18, 86/18) dalje skraćeno TP Čl. 4. 39.
TOPLINSKI MOSTOVI IZRAČUN PO HRN EN ISO 14683 U organizaciji: TEHNIČKI PROPIS O RACIONALNOJ UPORABI ENERGIJE I TOPLINSKOJ ZAŠTITI U ZGRADAMA (NN 128/15, 70/18, 73/18, 86/18) dalje skraćeno TP Čl. 4. 39.
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA Seminarski rad u okviru predmeta Računalna forenzika BETTER PORTABLE GRAPHICS FORMAT Matej
 SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA Seminarski rad u okviru predmeta Računalna forenzika BETTER PORTABLE GRAPHICS FORMAT Matej Crnac Zagreb, siječanj 2018 Sadržaj Uvod 2 BPG format
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA Seminarski rad u okviru predmeta Računalna forenzika BETTER PORTABLE GRAPHICS FORMAT Matej Crnac Zagreb, siječanj 2018 Sadržaj Uvod 2 BPG format
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA DIPLOMSKI RAD br Učenje dubokih korespondencijskih metrika trojnim gubitkom Marin Ko
 SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA DIPLOMSKI RAD br. 1729 Učenje dubokih korespondencijskih metrika trojnim gubitkom Marin Kostelac Zagreb, srpanj 2018. Umjesto ove stranice umetnite
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA DIPLOMSKI RAD br. 1729 Učenje dubokih korespondencijskih metrika trojnim gubitkom Marin Kostelac Zagreb, srpanj 2018. Umjesto ove stranice umetnite
18. ožujka Državno natjecanje / Osnovna škola (6. razred) Primjena algoritama (Basic/Python/Pascal/C/C++) Sadržaj Zadaci... 1 Zadatak: Kineski..
 18. ožujka 2015. Državno natjecanje / Primjena algoritama (Basic/Python/Pascal/C/C++) Sadržaj Zadaci... 1 Zadatak: Kineski... 2 Zadatak: Zmija... 3 Zadatak: Vlakovi... 5 Zadaci U tablici možete pogledati
18. ožujka 2015. Državno natjecanje / Primjena algoritama (Basic/Python/Pascal/C/C++) Sadržaj Zadaci... 1 Zadatak: Kineski... 2 Zadatak: Zmija... 3 Zadatak: Vlakovi... 5 Zadaci U tablici možete pogledati
Matematika 1 - izborna
 3.3. NELINEARNE DIOFANTSKE JEDNADŽBE Navest ćemo sada neke metode rješavanja diofantskih jednadžbi koje su drugog i viših stupnjeva. Sve su te metode zapravo posebni oblici jedne opće metode, koja se naziva
3.3. NELINEARNE DIOFANTSKE JEDNADŽBE Navest ćemo sada neke metode rješavanja diofantskih jednadžbi koje su drugog i viših stupnjeva. Sve su te metode zapravo posebni oblici jedne opće metode, koja se naziva
Hej hej bojiš se matematike? Ma nema potrebe! Dobra priprema je pola obavljenog posla, a da bi bio izvrsno pripremljen tu uskačemo mi iz Štreberaja. D
 Hej hej bojiš se matematike? Ma nema potrebe! Dobra priprema je pola obavljenog posla, a da bi bio izvrsno pripremljen tu uskačemo mi iz Štreberaja. Donosimo ti primjere ispita iz matematike, s rješenjima.
Hej hej bojiš se matematike? Ma nema potrebe! Dobra priprema je pola obavljenog posla, a da bi bio izvrsno pripremljen tu uskačemo mi iz Štreberaja. Donosimo ti primjere ispita iz matematike, s rješenjima.
Algoritmi SŠ P1
 Državno natjecanje iz informatike Srednja škola Prvi dan natjecanja 2. ožujka 219. ime zadatka BADMINTON SJEME MANIPULATOR vremensko ograničenje 1 sekunda 1 sekunda 3 sekunde memorijsko ograničenje 512
Državno natjecanje iz informatike Srednja škola Prvi dan natjecanja 2. ožujka 219. ime zadatka BADMINTON SJEME MANIPULATOR vremensko ograničenje 1 sekunda 1 sekunda 3 sekunde memorijsko ograničenje 512
Optimizacija
 Optimizacija 1 / 43 2 / 43 Uvod u optimizaciju Zadana funkcija Uvod u optimizaciju f : R n R Cilj: Naći x, točku minimuma funkcije f : - Problem je jednostavno opisati x = arg min x R n f (x). - Rješavanje
Optimizacija 1 / 43 2 / 43 Uvod u optimizaciju Zadana funkcija Uvod u optimizaciju f : R n R Cilj: Naći x, točku minimuma funkcije f : - Problem je jednostavno opisati x = arg min x R n f (x). - Rješavanje
Napredno estimiranje strukture i gibanja kalibriranim parom kamera
 Napredno estimiranje strukture i gibanja kalibriranim parom kamera Ivan Krešo Mentor: Siniša Šegvić 3. srpnja 2013. Motivacija Stereo vid dvije kamere omogućavaju mjerenje dubine korespondentnih točaka
Napredno estimiranje strukture i gibanja kalibriranim parom kamera Ivan Krešo Mentor: Siniša Šegvić 3. srpnja 2013. Motivacija Stereo vid dvije kamere omogućavaju mjerenje dubine korespondentnih točaka
PowerPoint Presentation
 Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Орт колоквијум
 II колоквијум из Основа рачунарске технике I - 27/28 (.6.28.) Р е ш е њ е Задатак На улазе x, x 2, x 3, x 4 комбинационе мреже, са излазом z, долази четворобитни BCD број. Ако број са улаза при дељењу
II колоквијум из Основа рачунарске технике I - 27/28 (.6.28.) Р е ш е њ е Задатак На улазе x, x 2, x 3, x 4 комбинационе мреже, са излазом z, долази четворобитни BCD број. Ако број са улаза при дељењу
Odreivanje neodreenosti hadronske strukture metodama strojnog ucenja
 Odredivanje neodredenosti hadronske strukture metodama strojnog učenja Ivan Ćorić 1 Mentor: prof. Krešimir Kumerički 1 1 Prirodoslovno matematički fakultet, Fizički odsjek Sveučilište u Zagrebu 29. siječnja
Odredivanje neodredenosti hadronske strukture metodama strojnog učenja Ivan Ćorić 1 Mentor: prof. Krešimir Kumerički 1 1 Prirodoslovno matematički fakultet, Fizički odsjek Sveučilište u Zagrebu 29. siječnja
ПА-4 Машинско учење-алгоритми машинског учења
 ПА-4 Машинско учење-алгоритми машинског учења Машинско учење увод и основни појмови Деф: the desgn and development of algorthms that allow computers to mprove ther performance over tme based on data sensor
ПА-4 Машинско учење-алгоритми машинског учења Машинско учење увод и основни појмови Деф: the desgn and development of algorthms that allow computers to mprove ther performance over tme based on data sensor
12_Predavanja_OPE
 OSNOVE POSLOVNE EKONOMIJE 12. Kalkulacija Sadržaj izlaganja: 12. KALKULACIJA 12.1. Pojam kalkulacije 12.2. Elementi kalkulacije 12.3. Vrste kalkulacije 12.4. Metode kalkulacije 12.4.1. Kalkulacija cijene
OSNOVE POSLOVNE EKONOMIJE 12. Kalkulacija Sadržaj izlaganja: 12. KALKULACIJA 12.1. Pojam kalkulacije 12.2. Elementi kalkulacije 12.3. Vrste kalkulacije 12.4. Metode kalkulacije 12.4.1. Kalkulacija cijene
DUBINSKA ANALIZA PODATAKA
 DUBINSKA ANALIZA PODATAKA () ASOCIJACIJSKA PRAVILA (ENGL. ASSOCIATION RULE) Studeni 2018. Mario Somek SADRŽAJ Asocijacijska pravila? Oblici učenja pravila Podaci za analizu Algoritam Primjer Izvođenje
DUBINSKA ANALIZA PODATAKA () ASOCIJACIJSKA PRAVILA (ENGL. ASSOCIATION RULE) Studeni 2018. Mario Somek SADRŽAJ Asocijacijska pravila? Oblici učenja pravila Podaci za analizu Algoritam Primjer Izvođenje
Logičke izjave i logičke funkcije
 Logičke izjave i logičke funkcije Građa računala, prijenos podataka u računalu Što su logičke izjave? Logička izjava je tvrdnja koja može biti istinita (True) ili lažna (False). Ako je u logičkoj izjavi
Logičke izjave i logičke funkcije Građa računala, prijenos podataka u računalu Što su logičke izjave? Logička izjava je tvrdnja koja može biti istinita (True) ili lažna (False). Ako je u logičkoj izjavi
Daljinski upravljiva utičnica
 Zvonimir Miličević;Martin Berić SEMINARSKI RAD - SPVP Projekt u sklopu Pametna kuća Poznavanje ugradbenih računalnih sustava Načini upravljanja na daljinu 14. lipnja 2018 Sažetak Svakome se dogodilo da
Zvonimir Miličević;Martin Berić SEMINARSKI RAD - SPVP Projekt u sklopu Pametna kuća Poznavanje ugradbenih računalnih sustava Načini upravljanja na daljinu 14. lipnja 2018 Sažetak Svakome se dogodilo da
1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan
 1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan jednačinom oblika: a 11 x 2 + 2a 12 xy + a 22 y 2
1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan jednačinom oblika: a 11 x 2 + 2a 12 xy + a 22 y 2
Microsoft PowerPoint - Predavanje3.ppt
 Фрактална геометрија и фрактали у архитектури функционални системи Улаз Низ правила (функција F) Излаз Фрактална геометрија и фрактали у архитектури функционални системи Функционални систем: Улаз Низ правила
Фрактална геометрија и фрактали у архитектури функционални системи Улаз Низ правила (функција F) Излаз Фрактална геометрија и фрактали у архитектури функционални системи Функционални систем: Улаз Низ правила
Техничко решење: Софтвер за симулацију стохастичког ортогоналног мерила сигнала, његовог интеграла и диференцијала Руководилац пројекта: Владимир Вуји
 Техничко решење: Софтвер за симулацију стохастичког ортогоналног мерила сигнала, његовог интеграла и диференцијала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Велибор
Техничко решење: Софтвер за симулацију стохастичког ортогоналног мерила сигнала, његовог интеграла и диференцијала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Велибор
Elementi praćenja i ocjenjivanja za nastavni predmet Matematika u 4. razredu Elementi praćenja i ocjenjivanja za nastavni predmet Matematika u 4. razr
 Elementi praćenja i ocjenjivanja za nastavni predmet Matematika u 4. razredu ODLIČAN (5) navodi primjer kuta kao dijela ravnine omeđenog polupravcima analizira i uspoređuje vrh i krakove kuta analizira
Elementi praćenja i ocjenjivanja za nastavni predmet Matematika u 4. razredu ODLIČAN (5) navodi primjer kuta kao dijela ravnine omeđenog polupravcima analizira i uspoređuje vrh i krakove kuta analizira
Slide 1
 0(a) 0(b) 0(c) 0(d) 0(e) :: :: Neke fizikalne veličine poput indeksa loma u anizotropnim sredstvima ovise o iznosu i smjeru, a nisu vektori. Stoga se namede potreba poopdavanja. Međutim, fizikalne veličine,
0(a) 0(b) 0(c) 0(d) 0(e) :: :: Neke fizikalne veličine poput indeksa loma u anizotropnim sredstvima ovise o iznosu i smjeru, a nisu vektori. Stoga se namede potreba poopdavanja. Međutim, fizikalne veličine,
(Microsoft Word - Dr\236avna matura - kolovoz ni\236a razina - rje\232enja)
 1. C. Imamo redom: I. ZADATCI VIŠESTRUKOGA IZBORA. B. Imamo redom: 0.3 0. 8 7 8 19 ( 3) 4 : = 9 4 = 9 4 = 9 = =. 0. 0.3 3 3 3 3 0 1 3 + 1 + 4 8 5 5 = = = = = = 0 1 3 0 1 3 0 1+ 3 ( : ) ( : ) 5 5 4 0 3.
1. C. Imamo redom: I. ZADATCI VIŠESTRUKOGA IZBORA. B. Imamo redom: 0.3 0. 8 7 8 19 ( 3) 4 : = 9 4 = 9 4 = 9 = =. 0. 0.3 3 3 3 3 0 1 3 + 1 + 4 8 5 5 = = = = = = 0 1 3 0 1 3 0 1+ 3 ( : ) ( : ) 5 5 4 0 3.
Microsoft PowerPoint - SEP-2013-CAS02
 STRATEGIJE E ZA ELEKTRONSKO POSLOVANJE STRATEGIJE ZA ELEKTRONSKO POSLOVANJE Elektronsko poslovanje ne predstavlja samo dodatak tradicionalnom, već ono predstavlja revoluciju u poslovanju. Ono omogućava
STRATEGIJE E ZA ELEKTRONSKO POSLOVANJE STRATEGIJE ZA ELEKTRONSKO POSLOVANJE Elektronsko poslovanje ne predstavlja samo dodatak tradicionalnom, već ono predstavlja revoluciju u poslovanju. Ono omogućava
Toplinska i električna vodljivost metala
 Električna vodljivost metala Cilj vježbe Određivanje koeficijenta električne vodljivosti bakra i aluminija U-I metodom. Teorijski dio Eksperimentalno je utvrđeno da otpor ne-ohmskog vodiča raste s porastom
Električna vodljivost metala Cilj vježbe Određivanje koeficijenta električne vodljivosti bakra i aluminija U-I metodom. Teorijski dio Eksperimentalno je utvrđeno da otpor ne-ohmskog vodiča raste s porastom
(Microsoft Word vje\236ba - LIMES FUNKCIJE.doc)
 Zadatak Pokažite, koristeći svojstva esa, da je ( 6 ) 5 Svojstva esa funkcije u točki: Ako je k konstanta, k k c c c f ( ) L i g( ) M, tada vrijedi: c c [ f ( ) ± g( ) ] c c f ( ) ± g( ) L ± M c [ f (
Zadatak Pokažite, koristeći svojstva esa, da je ( 6 ) 5 Svojstva esa funkcije u točki: Ako je k konstanta, k k c c c f ( ) L i g( ) M, tada vrijedi: c c [ f ( ) ± g( ) ] c c f ( ) ± g( ) L ± M c [ f (
(Microsoft Word - Dr\236avna matura - svibanj osnovna razina - rje\232enja)
 I. ZADATCI VIŠESTRUKOGA IZBORA 1. A. Svih pet zadanih razlomaka svedemo na najmanji zajednički nazivnik. Taj nazivnik je najmanji zajednički višekratnik brojeva i 3, tj. NZV(, 3) = 6. Dobijemo: 15 1, 6
I. ZADATCI VIŠESTRUKOGA IZBORA 1. A. Svih pet zadanih razlomaka svedemo na najmanji zajednički nazivnik. Taj nazivnik je najmanji zajednički višekratnik brojeva i 3, tj. NZV(, 3) = 6. Dobijemo: 15 1, 6
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Ivana Šore REKURZIVNOST REALNIH FUNKCIJA Diplomski rad Voditelj rada: doc.
 SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Ivana Šore REKURZIVNOST REALNIH FUNKCIJA Diplomski rad Voditelj rada: doc.dr.sc. Zvonko Iljazović Zagreb, rujan, 2015. Ovaj diplomski
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Ivana Šore REKURZIVNOST REALNIH FUNKCIJA Diplomski rad Voditelj rada: doc.dr.sc. Zvonko Iljazović Zagreb, rujan, 2015. Ovaj diplomski
Skalarne funkcije više varijabli Parcijalne derivacije Skalarne funkcije više varijabli i parcijalne derivacije Franka Miriam Brückler
 i parcijalne derivacije Franka Miriam Brückler Jednadžba stanja idealnog plina uz p = nrt V f (x, y, z) = xy z x = n mol, y = T K, z = V L, f == p Pa. Pritom je kodomena od f skup R, a domena je Jednadžba
i parcijalne derivacije Franka Miriam Brückler Jednadžba stanja idealnog plina uz p = nrt V f (x, y, z) = xy z x = n mol, y = T K, z = V L, f == p Pa. Pritom je kodomena od f skup R, a domena je Jednadžba
Microsoft PowerPoint - podatkovni promet za objavu.pptx
 1 2 3 Što je složaj protokola (protocol suite)? Pojedini protokol se odnosi samo na jedno pitanje koje omogućava komunikaciju. Kada se kombinira više protokola, grupa protokola koja je rezultat takve kombinacije
1 2 3 Što je složaj protokola (protocol suite)? Pojedini protokol se odnosi samo na jedno pitanje koje omogućava komunikaciju. Kada se kombinira više protokola, grupa protokola koja je rezultat takve kombinacije
Рачунарска интелигенција
 Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Interpretacija čuda pomoću teorije determinističkog kaosa (Jerko Kolovrat, KBF Split; Marija Todorić, PMF Zagreb) Postoje razne teme koje zaokupljaju
 Interpretacija čuda pomoću teorije determinističkog kaosa (Jerko Kolovrat, KBF Split; Marija Todorić, PMF Zagreb) Postoje razne teme koje zaokupljaju ljudski um i tjeraju ga da prema njima zauzme stav
Interpretacija čuda pomoću teorije determinističkog kaosa (Jerko Kolovrat, KBF Split; Marija Todorić, PMF Zagreb) Postoje razne teme koje zaokupljaju ljudski um i tjeraju ga da prema njima zauzme stav
4
 4.1.2 Eksperimentalni rezultati Rezultati eksperimentalnog istraživanja obrađeni su u programu za digitalno uređivanje audio zapisa (Coll Edit). To je program koji omogućava široku obradu audio zapisa.
4.1.2 Eksperimentalni rezultati Rezultati eksperimentalnog istraživanja obrađeni su u programu za digitalno uređivanje audio zapisa (Coll Edit). To je program koji omogućava široku obradu audio zapisa.
Državna matura iz informatike
 DRŽAVNA MATURA IZ INFORMATIKE U ŠK. GOD. 2013./14. 2016./17. SADRŽAJ Osnovne informacije o ispitu iz informatike Područja ispitivanja Pragovi prolaznosti u 2014./15. Primjeri zadataka po područjima ispitivanja
DRŽAVNA MATURA IZ INFORMATIKE U ŠK. GOD. 2013./14. 2016./17. SADRŽAJ Osnovne informacije o ispitu iz informatike Područja ispitivanja Pragovi prolaznosti u 2014./15. Primjeri zadataka po područjima ispitivanja
(Microsoft Word - Rje\232enja zadataka)
 1. D. Svedimo sve razlomke na jedinstveni zajednički nazivnik. Lako provjeravamo da vrijede rastavi: 85 = 17 5, 187 = 17 11, 170 = 17 10, pa je zajednički nazivnik svih razlomaka jednak Tako sada imamo:
1. D. Svedimo sve razlomke na jedinstveni zajednički nazivnik. Lako provjeravamo da vrijede rastavi: 85 = 17 5, 187 = 17 11, 170 = 17 10, pa je zajednički nazivnik svih razlomaka jednak Tako sada imamo:
Numerička matematika 11. predavanje dodatak Saša Singer web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb NumMat 2019, 11. p
 Numerička matematika 11. predavanje dodatak Saša Singer singer@math.hr web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb NumMat 2019, 11. predavanje dodatak p. 1/46 Sadržaj predavanja dodatka
Numerička matematika 11. predavanje dodatak Saša Singer singer@math.hr web.math.pmf.unizg.hr/~singer PMF Matematički odsjek, Zagreb NumMat 2019, 11. predavanje dodatak p. 1/46 Sadržaj predavanja dodatka
VELEUČILIŠTE VELIKA GORICA REZULTATI STUDENTSKE ANKETE PROVEDENE NA VELEUČILIŠTU VELIKA GORICA ZA ZIMSKI SEMESTAR AKADEMSKE 2013/2014 GODINE 1. Uvod E
 REZULTATI STUDENTSKE ANKETE PROVEDENE NA VELEUČILIŠTU VELIKA GORICA ZA ZIMSKI SEMESTAR AKADEMSKE 2013/2014 GODINE 1. Uvod Evaluacijska anketa nastavnika i nastavnih predmeta provedena je putem interneta.
REZULTATI STUDENTSKE ANKETE PROVEDENE NA VELEUČILIŠTU VELIKA GORICA ZA ZIMSKI SEMESTAR AKADEMSKE 2013/2014 GODINE 1. Uvod Evaluacijska anketa nastavnika i nastavnih predmeta provedena je putem interneta.
(Microsoft Word - MATB - kolovoz osnovna razina - rje\232enja zadataka)
 . B. Zapišimo zadane brojeve u obliku beskonačno periodičnih decimalnih brojeva: 3 4 = 0.7, = 0.36. Prvi od navedenih četiriju brojeva je manji od 3 4, dok su treći i četvrti veći od. Jedini broj koji
. B. Zapišimo zadane brojeve u obliku beskonačno periodičnih decimalnih brojeva: 3 4 = 0.7, = 0.36. Prvi od navedenih četiriju brojeva je manji od 3 4, dok su treći i četvrti veći od. Jedini broj koji
Sveučilište J.J. Strossmayera Fizika 2 FERIT Predložak za laboratorijske vježbe Određivanje relativne permitivnosti sredstva Cilj vježbe Određivanje r
 Sveučilište J.J. Strossmayera Fizika 2 Predložak za laboratorijske vježbe Cilj vježbe Određivanje relativne permitivnosti stakla, plastike, papira i zraka mjerenjem kapaciteta pločastog kondenzatora U-I
Sveučilište J.J. Strossmayera Fizika 2 Predložak za laboratorijske vježbe Cilj vježbe Određivanje relativne permitivnosti stakla, plastike, papira i zraka mjerenjem kapaciteta pločastog kondenzatora U-I
P11.3 Analiza zivotnog veka, Graf smetnji
 Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
1 MATEMATIKA 1 (prva zadaća) Vektori i primjene 1. U trokutu ABC točke M i N dijele stranicu AB na tri jednaka dijela. O
 http://www.fsb.hr/matematika/ (prva zadać Vektori i primjene. U trokutu ABC točke M i N dijele stranicu AB na tri jednaka dijela. Označite CA= a, CB= b i izrazite vektore CM i CN pomoću vektora a i b..
http://www.fsb.hr/matematika/ (prva zadać Vektori i primjene. U trokutu ABC točke M i N dijele stranicu AB na tri jednaka dijela. Označite CA= a, CB= b i izrazite vektore CM i CN pomoću vektora a i b..
Objektno orijentirano modeliranje
 Sveučilište u Rijeci ODJEL ZA INFORMATIKU Akademska 2018./2019. godina OBJEKTNO ORIJENTIRANO MODELIRANJE Studij: Preddiplomski studij informatike (JP) Preddiplomski dvopredmetni studij informatike (DP)
Sveučilište u Rijeci ODJEL ZA INFORMATIKU Akademska 2018./2019. godina OBJEKTNO ORIJENTIRANO MODELIRANJE Studij: Preddiplomski studij informatike (JP) Preddiplomski dvopredmetni studij informatike (DP)
Podružnica za građenje
 Dodatak A OPIS USLUGA DODATAK A-1 PROJEKTNI ZADATAK Revizija scenarija i algoritama Regionalnih centara za nadzor i upravljanje prometom na autocestama Zagreb, srpanj 2019. 1. Uvod Sve veći porast prometa
Dodatak A OPIS USLUGA DODATAK A-1 PROJEKTNI ZADATAK Revizija scenarija i algoritama Regionalnih centara za nadzor i upravljanje prometom na autocestama Zagreb, srpanj 2019. 1. Uvod Sve veći porast prometa
NAZIV PREDMETA UNUTARNJETRGOVINSKO POSLOVANJE I Kod Godina studija 2. Nositelj/i predmeta dr.sc. Ivana Plazibat, prof. Bodovna vrijednost 6 ECTS v.š.
 NAZIV PREDMETA UNUTARNJETRGOVINSKO POSLOVANJE I Kod Godina studija 2. Nositelj/i predmeta dr.sc. Ivana Plazibat, prof. Bodovna vrijednost 6 ECTS v.š. (ECTS) Suradnici nema Način izvođenja nastave P S V
NAZIV PREDMETA UNUTARNJETRGOVINSKO POSLOVANJE I Kod Godina studija 2. Nositelj/i predmeta dr.sc. Ivana Plazibat, prof. Bodovna vrijednost 6 ECTS v.š. (ECTS) Suradnici nema Način izvođenja nastave P S V
Test ispravio: (1) (2) Ukupan broj bodova: 21. veljače od 13:00 do 14:00 Županijsko natjecanje / Osnove informatike Osnovne škole Ime i prezime
 Test ispravio: () () Ukupan broj bodova:. veljače 04. od 3:00 do 4:00 Ime i prezime Razred Škola Županija Mentor Sadržaj Upute za natjecatelje... Zadaci... Upute za natjecatelje Vrijeme pisanja: 60 minuta
Test ispravio: () () Ukupan broj bodova:. veljače 04. od 3:00 do 4:00 Ime i prezime Razred Škola Županija Mentor Sadržaj Upute za natjecatelje... Zadaci... Upute za natjecatelje Vrijeme pisanja: 60 minuta
UAAG Osnovne algebarske strukture 5. Vektorski prostori Borka Jadrijević
 Osnovne algebarske strukture 5. Vektorski prostori Borka Jadrijević Osnovne algebarske strukture5. Vektorski prostori 2 5.1 Unutarnja i vanjska množenja Imamo dvije vrste algebarskih operacija, tzv. unutarnja
Osnovne algebarske strukture 5. Vektorski prostori Borka Jadrijević Osnovne algebarske strukture5. Vektorski prostori 2 5.1 Unutarnja i vanjska množenja Imamo dvije vrste algebarskih operacija, tzv. unutarnja
AM_Ple_NonLegReport
 9.2.2017 A8-0005/9 Amandman 9 Stavak 1.a (novi) 1 a. poziva Komisiju da predloži sljedeće zajedničke europske definicije: umjetna inteligencija je automatizirani sustav s mogućnošću simulacije nekih ljudskih
9.2.2017 A8-0005/9 Amandman 9 Stavak 1.a (novi) 1 a. poziva Komisiju da predloži sljedeće zajedničke europske definicije: umjetna inteligencija je automatizirani sustav s mogućnošću simulacije nekih ljudskih
Posjet poduzeću Model Pakiranja d.d je u sklopu kolegija Menadžment ljudskih potencijala organizirana terenska nastava i posjet poduzeću M
 Posjet poduzeću Model Pakiranja d.d. 23.5.2019. je u sklopu kolegija Menadžment ljudskih potencijala organizirana terenska nastava i posjet poduzeću Model Pakiranja. Studente je kroz poduzeće vodio g.
Posjet poduzeću Model Pakiranja d.d. 23.5.2019. je u sklopu kolegija Menadžment ljudskih potencijala organizirana terenska nastava i posjet poduzeću Model Pakiranja. Studente je kroz poduzeće vodio g.
Microsoft Word - 09_Frenetove formule
 6 Frenet- Serret-ove formule x : 0,L Neka je regularna parametrizaija krivulje C u prostoru parametru s ) zadana vektorskom jednadžbom: x s x s i y s j z s k x s, y s, z s C za svaki 0, L Pritom je zbog
6 Frenet- Serret-ove formule x : 0,L Neka je regularna parametrizaija krivulje C u prostoru parametru s ) zadana vektorskom jednadžbom: x s x s i y s j z s k x s, y s, z s C za svaki 0, L Pritom je zbog
NAZIV PREDMETA OBLIKOVANJE WEB STRANICA Kod SIT132 Godina studija 3. Bodovna vrijednost Nositelj/i predmeta Haidi Božiković, predavač 6 (ECTS) Suradni
 NAZIV PREDMETA OBLIKOVANJE WEB STRANICA Kod SIT132 Godina studija 3. Bodovna vrijednost Nositelj/i predmeta Haidi Božiković, predavač 6 (ECTS) Suradnici Status predmeta Ciljevi predmeta Uvjeti za upis
NAZIV PREDMETA OBLIKOVANJE WEB STRANICA Kod SIT132 Godina studija 3. Bodovna vrijednost Nositelj/i predmeta Haidi Božiković, predavač 6 (ECTS) Suradnici Status predmeta Ciljevi predmeta Uvjeti za upis
Uvod u obične diferencijalne jednadžbe Metoda separacije varijabli Obične diferencijalne jednadžbe Franka Miriam Brückler
 Obične diferencijalne jednadžbe Franka Miriam Brückler Primjer Deriviranje po x je linearan operator d dx kojemu recimo kao domenu i kodomenu uzmemo (beskonačnodimenzionalni) vektorski prostor funkcija
Obične diferencijalne jednadžbe Franka Miriam Brückler Primjer Deriviranje po x je linearan operator d dx kojemu recimo kao domenu i kodomenu uzmemo (beskonačnodimenzionalni) vektorski prostor funkcija
7. predavanje Vladimir Dananić 14. studenoga Vladimir Dananić () 7. predavanje 14. studenoga / 16
 7. predavanje Vladimir Dananić 14. studenoga 2011. Vladimir Dananić () 7. predavanje 14. studenoga 2011. 1 / 16 Sadržaj 1 Operator kutne količine gibanja 2 3 Zadatci Vladimir Dananić () 7. predavanje 14.
7. predavanje Vladimir Dananić 14. studenoga 2011. Vladimir Dananić () 7. predavanje 14. studenoga 2011. 1 / 16 Sadržaj 1 Operator kutne količine gibanja 2 3 Zadatci Vladimir Dananić () 7. predavanje 14.
10_Perdavanja_OPE [Compatibility Mode]
![10_Perdavanja_OPE [Compatibility Mode] 10_Perdavanja_OPE [Compatibility Mode]](/thumbs/101/152226818.jpg) OSNOVE POSLOVNE EKONOMIJE Predavanja: 10. cjelina 10.1. OSNOVNI POJMOVI Proizvodnja je djelatnost kojom se uz pomoć ljudskog rada i tehničkih sredstava predmeti rada pretvaraju u proizvode i usluge. S
OSNOVE POSLOVNE EKONOMIJE Predavanja: 10. cjelina 10.1. OSNOVNI POJMOVI Proizvodnja je djelatnost kojom se uz pomoć ljudskog rada i tehničkih sredstava predmeti rada pretvaraju u proizvode i usluge. S
УНИВЕРЗИТЕТ У БЕОГРАДУ МАШИНСКИ ФАКУЛТЕТ Предмет: КОМПЈУТЕРСКА СИМУЛАЦИЈА И ВЕШТАЧКА ИНТЕЛИГЕНЦИЈА Задатак број: Лист/листова: 1/1 Задатак 5.1 Pостоје
 Лист/листова: 1/1 Задатак 5.1 Pостоје софтвери за препознавање бар кодова који знатно олакшавају велики број операција које захтевају препознавање објеката. Слика 1: Приказ свих слова за које је ART-1
Лист/листова: 1/1 Задатак 5.1 Pостоје софтвери за препознавање бар кодова који знатно олакшавају велики број операција које захтевају препознавање објеката. Слика 1: Приказ свих слова за које је ART-1
Microsoft Word - V03-Prelijevanje.doc
 Praktikum iz hidraulike Str. 3-1 III vježba Prelijevanje preko širokog praga i preljeva praktičnog profila Mali stakleni žlijeb je izrađen za potrebe mjerenja pojedinih hidrauličkih parametara tečenja
Praktikum iz hidraulike Str. 3-1 III vježba Prelijevanje preko širokog praga i preljeva praktičnog profila Mali stakleni žlijeb je izrađen za potrebe mjerenja pojedinih hidrauličkih parametara tečenja
8 2 upiti_izvjesca.indd
 1 2. Baze podataka Upiti i izvješća baze podataka Na početku cjeline o bazama podataka napravili ste plošnu bazu podataka o natjecanjima učenika. Sada ćete izraditi relacijsku bazu u Accessu o učenicima
1 2. Baze podataka Upiti i izvješća baze podataka Na početku cjeline o bazama podataka napravili ste plošnu bazu podataka o natjecanjima učenika. Sada ćete izraditi relacijsku bazu u Accessu o učenicima
Microsoft Word - 24ms241
 Zadatak (Branko, srednja škola) Parabola zadana jednadžbom = p x prolazi točkom tangente na tu parabolu u točki A? A,. A. x + = 0 B. x 8 = 0 C. x = 0 D. x + + = 0 Rješenje b a b a b a =, =. c c b a Kako
Zadatak (Branko, srednja škola) Parabola zadana jednadžbom = p x prolazi točkom tangente na tu parabolu u točki A? A,. A. x + = 0 B. x 8 = 0 C. x = 0 D. x + + = 0 Rješenje b a b a b a =, =. c c b a Kako
Microsoft PowerPoint - GR_MbIS_12_IDEF
 Menadžment poslovnih informacionih sistema - 12 metode modeliranja funkcija pripremila Doc. dr Gordana Radić Integfated DEFinition Definicija: je metoda (jezik) modeliranja bazirana je na kombinaciji grafike
Menadžment poslovnih informacionih sistema - 12 metode modeliranja funkcija pripremila Doc. dr Gordana Radić Integfated DEFinition Definicija: je metoda (jezik) modeliranja bazirana je na kombinaciji grafike
Veeeeeliki brojevi
 Matematička gimnazija Nedelja informatike 3 12. decembar 2016. Uvod Postoji 10 tipova ljudi na svetu, oni koji razumeju binarni sistem, oni koji ne razumeju binarni sistem i oni koji nisu očekivali šalu
Matematička gimnazija Nedelja informatike 3 12. decembar 2016. Uvod Postoji 10 tipova ljudi na svetu, oni koji razumeju binarni sistem, oni koji ne razumeju binarni sistem i oni koji nisu očekivali šalu
Microsoft Word - 24ms221
 Zadatak (Katarina, maturantica) Kružnica dira os apscisa u točki (3, 0) i siječe os ordinata u točki (0, 0). Koliki je polumjer te kružnice? A. 5 B. 5.45 C. 6.5. 7.38 Rješenje Kružnica je skup svih točaka
Zadatak (Katarina, maturantica) Kružnica dira os apscisa u točki (3, 0) i siječe os ordinata u točki (0, 0). Koliki je polumjer te kružnice? A. 5 B. 5.45 C. 6.5. 7.38 Rješenje Kružnica je skup svih točaka
РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена ) Прва година: ПРВА ГОДИНА - сви сем информатике Име пр
 РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена 23.01.2017.) Прва година: ПРВА ГОДИНА - сви сем информатике Име предмета Датум и термин одржавања писменог дела испита
РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена 23.01.2017.) Прва година: ПРВА ГОДИНА - сви сем информатике Име предмета Датум и термин одржавања писменог дела испита
Uvod u računarstvo 2+2
 Programiranje 2 doc.dr.sc. Goranka Nogo PMF Matematički odsjek, Zagreb Kontakt ured: 228, drugi kat e-mail: nogo@math.hr konzultacije: četvrtak, 12:00-14:00 petak, 11:00-12:00 neki drugi termin, uz prethodni
Programiranje 2 doc.dr.sc. Goranka Nogo PMF Matematički odsjek, Zagreb Kontakt ured: 228, drugi kat e-mail: nogo@math.hr konzultacije: četvrtak, 12:00-14:00 petak, 11:00-12:00 neki drugi termin, uz prethodni
PuTTY CERT.hr-PUBDOC
 PuTTY CERT.hr-PUBDOC-2018-12-371 Sadržaj 1 UVOD... 3 2 INSTALACIJA ALATA PUTTY... 4 3 KORIŠTENJE ALATA PUTTY... 7 3.1 POVEZIVANJE S UDALJENIM RAČUNALOM... 7 3.2 POHRANA PROFILA KORISNIČKIH SJEDNICA...
PuTTY CERT.hr-PUBDOC-2018-12-371 Sadržaj 1 UVOD... 3 2 INSTALACIJA ALATA PUTTY... 4 3 KORIŠTENJE ALATA PUTTY... 7 3.1 POVEZIVANJE S UDALJENIM RAČUNALOM... 7 3.2 POHRANA PROFILA KORISNIČKIH SJEDNICA...
Slide 1
 , In Cubis d.o.o. Dani hrvatskog osiguranja Opatija, 6.11.2014. Funkcije informacijskog sustava u osiguranju Informacijski sustav... Čuva najvrijedniju imovinu podatke Automatizira poslovne procese Otvara
, In Cubis d.o.o. Dani hrvatskog osiguranja Opatija, 6.11.2014. Funkcije informacijskog sustava u osiguranju Informacijski sustav... Čuva najvrijedniju imovinu podatke Automatizira poslovne procese Otvara
Prikaz slike na monitoru i pisaču
 CRT monitori s katodnom cijevi i LCD monitori na bazi tekućih kristala koji su gotovo istisnuli iz upotrebe prethodno navedene. LED monitori- Light Emitting Diode, zasniva se na elektrodama i diodama koje
CRT monitori s katodnom cijevi i LCD monitori na bazi tekućih kristala koji su gotovo istisnuli iz upotrebe prethodno navedene. LED monitori- Light Emitting Diode, zasniva se na elektrodama i diodama koje
Technology management performance indicators in global country rankings
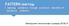 PATTERN метод (Planning Assistance Through Technical Evaluation of Relevance Numbers) Менаџмент технологије и развоја 2018/19 PATTERN метод Метод нормативног предвиђања Метод стабла значајности Стабло
PATTERN метод (Planning Assistance Through Technical Evaluation of Relevance Numbers) Менаџмент технологије и развоја 2018/19 PATTERN метод Метод нормативног предвиђања Метод стабла значајности Стабло
Seminar 13 (Tok funkcije) Obavezna priprema za seminar nalazi se na drugoj stranici ovog materijala. Ove materijale obražujemo na seminarima do kraja
 Seminar 13 (Tok funkcije) Obavezna priprema za seminar nalazi se na drugoj stranici ovog materijala. Ove materijale obražujemo na seminarima do kraja semestra. Potrebno predznanje Ovaj seminar saºima sva
Seminar 13 (Tok funkcije) Obavezna priprema za seminar nalazi se na drugoj stranici ovog materijala. Ove materijale obražujemo na seminarima do kraja semestra. Potrebno predznanje Ovaj seminar saºima sva
Zadatak 1 U tablici se nalaze podaci dobiveni odredivanjem bilirubina u 24 uzoraka seruma (µmol/l):
 Zadatak 1 U tablici se nalaze podaci dobiveni odredivanjem bilirubina u 4 uzoraka seruma (µmol/l): 1.8 13.8 15.9 14.7 13.7 14.7 13.5 1.4 13 14.4 15 13.1 13. 15.1 13.3 14.4 1.4 15.3 13.4 15.7 15.1 14.5
Zadatak 1 U tablici se nalaze podaci dobiveni odredivanjem bilirubina u 4 uzoraka seruma (µmol/l): 1.8 13.8 15.9 14.7 13.7 14.7 13.5 1.4 13 14.4 15 13.1 13. 15.1 13.3 14.4 1.4 15.3 13.4 15.7 15.1 14.5
1
 Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA Lokalizacija karakterističnih točaka lica u videu Generalić Boris Gulan Filip Kopljar Damir Miličević Andrija Nu
 FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA Lokalizacija karakterističnih točaka lica u videu Generalić Boris Gulan Filip Kopljar Damir Miličević Andrija Nuić Hrvoje Šarić Fredi Zadro Tvrtko Zagreb, siječanj
FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA Lokalizacija karakterističnih točaka lica u videu Generalić Boris Gulan Filip Kopljar Damir Miličević Andrija Nuić Hrvoje Šarić Fredi Zadro Tvrtko Zagreb, siječanj
Može li učenje tablice množenja biti zabavno?
 Mogu li besplatne igre na tabletima potaknuti učenike na učenje tablice množenja i dijeljenja? Sanja Loparić, prof. matematike i informatike Tehnička škola Čakovec Rovinj, 11.11.2016. Kad djeca nisu u
Mogu li besplatne igre na tabletima potaknuti učenike na učenje tablice množenja i dijeljenja? Sanja Loparić, prof. matematike i informatike Tehnička škola Čakovec Rovinj, 11.11.2016. Kad djeca nisu u
Орт колоквијум
 Испит из Основа рачунарске технике - / (6.6.. Р е ш е њ е Задатак Комбинациона мрежа има пет улаза, по два за број освојених сетова тенисера и један сигнал који одлучује ко је бољи уколико је резултат
Испит из Основа рачунарске технике - / (6.6.. Р е ш е њ е Задатак Комбинациона мрежа има пет улаза, по два за број освојених сетова тенисера и један сигнал који одлучује ко је бољи уколико је резултат
CARNET Helpdesk - Podrška obrazovnom sustavu e-dnevnik upute za nadzor razrednih knjiga tel: fax: mail:
 Sadržaj... 1 1. Predgovor... 2 2. Prijava u sustav... 2 3. Postavke... 3 4. Kreiranje zahtjeva za nadzorom razrednih knjiga... 4 5. Pregled razredne knjige... 6 5.1 Dnevnik rada... 7 5.2 Imenik... 11 5.3
Sadržaj... 1 1. Predgovor... 2 2. Prijava u sustav... 2 3. Postavke... 3 4. Kreiranje zahtjeva za nadzorom razrednih knjiga... 4 5. Pregled razredne knjige... 6 5.1 Dnevnik rada... 7 5.2 Imenik... 11 5.3
JMBAG IME I PREZIME BROJ BODOVA MJERA I INTEGRAL završni ispit 6. srpnja (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni!) 1.
 MJERA I INTEGRAL završni ispit 6. srpnja 208. (Knjige bilježnice dodatni papiri i kalkulatori nisu dozvoljeni!). (8 bodova) Kao na predavanjima za d N sa P d : a b ] a d b d ] : a i b i R a i b i za i
MJERA I INTEGRAL završni ispit 6. srpnja 208. (Knjige bilježnice dodatni papiri i kalkulatori nisu dozvoljeni!). (8 bodova) Kao na predavanjima za d N sa P d : a b ] a d b d ] : a i b i R a i b i za i
Infokup - Školsko Osnovne škole Algoritmi BaPaCpp
 21.. siječnja 2013.. od 1:30 do 16:30 Školsko natjecanje / Algoritmi (Basic/Pascal/C/C++) Sadržaj Zadaci... 1 Zadatak: Napolitanke... 2 Zadatak: Peking... 3 Zadatak: Joker... Zadaci U tablici možete pogledati
21.. siječnja 2013.. od 1:30 do 16:30 Školsko natjecanje / Algoritmi (Basic/Pascal/C/C++) Sadržaj Zadaci... 1 Zadatak: Napolitanke... 2 Zadatak: Peking... 3 Zadatak: Joker... Zadaci U tablici možete pogledati
Development Case
 Tehnička dokumentacija Verzija Studentski tim: Nastavnik: < izv. prof. dr. sc. Nikola Mišković> FER 2 -
Tehnička dokumentacija Verzija Studentski tim: Nastavnik: < izv. prof. dr. sc. Nikola Mišković> FER 2 -
Vrjednovanje diplomskih studija od strane studenata koji su tijekom akademske godine 2015./2016. završili studij Fakultet organizacije i informatike I
 Vrjednovanje diplomskih studija od strane studenata koji su tijekom akademske godine 2015./2016. završili studij Fakultet organizacije i informatike Informacijsko i programsko inženjerstvo Ured za upravljanje
Vrjednovanje diplomskih studija od strane studenata koji su tijekom akademske godine 2015./2016. završili studij Fakultet organizacije i informatike Informacijsko i programsko inženjerstvo Ured za upravljanje
Microsoft Word - Svrha projekta.doc
 S V E U Č I L I Š T E U Z A G R E B U FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA Zavod za elektroničke sustave i obradbu informacija FER 2 program, 1. godina diplomskog studija Kolegij: Sustavi za praćenje
S V E U Č I L I Š T E U Z A G R E B U FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA Zavod za elektroničke sustave i obradbu informacija FER 2 program, 1. godina diplomskog studija Kolegij: Sustavi za praćenje
Microsoft Word - IP_Tables_programski_alat.doc
 1. IP Tables alat (pregled naredbi) 1.1. Osnovne IP Tables naredbe za filtriranje paketa U ovom poglavlju opisane su osnovne IP Tables naredbe korištene za filtriranje paketa. S programskim paketom IP
1. IP Tables alat (pregled naredbi) 1.1. Osnovne IP Tables naredbe za filtriranje paketa U ovom poglavlju opisane su osnovne IP Tables naredbe korištene za filtriranje paketa. S programskim paketom IP
