Microsoft PowerPoint - AT 3-2 .ppt
|
|
|
- Vojko Vodopivec
- пре 5 година
- Прикази:
Транскрипт
1 Алгоритам учења перцептрона Корак : Иницијализација. Нека је t=0 и нека вектор иницијалних тежинскиходноса w(t) R a дефинише иницијалнопресликавање од скривених неурона до излазног неурона. Корак : Изабрати стимулацију (подстреке) перцептрона примењујућиузоркеизобучавајућегскупа x k наслучајанначин, што се може исказати помоћу x k (t)=(s k (t),o k (t)) {0,}, где је o k циљни вектор, којипредстављазахтеваниодговорнастимулацију. Корак : Израчунати активацију неурона у скривеном слоју h k, на основуактивацијеулазнихнеурона, h k (t)= q(s k (t)). Корак 4: Израчунати активацију излазног неурона мреже r k, на основу активације неурона из скривеног слоја, r k (t)= f(net)= f(w(t) T, h k (t)), причемује f(net)=акоје net 0 и f(net)=0 акоје net < 0. Корак 5: Модификовати тежинске односе између скривених неурона иизлазногнеурона, w(t+)= w(t)+[ o k (t)- r k (t)]h k (t). Корак 6: Зауставитиучењеакоје t > t max или o k (t)= r k (t), за k=,...,n, иначенекаје t=t+итадајенеопходновратитисенакорак. 7/5
2 Детаљна анализа перцептрона у погледу могућности и ограничења примене Marvin Minsky и Seymour Papert (969) Главна карактеристика: линеарна дискриминациона функција у простору узорака у коначном броју итерација; y y x x a) Коректна класификација: самоза линеарно раздвајајуће класе узорака; а), самоједан процесирајући елемент перцептрона јепотребан, собзиром да је цела површина раздељена једном правом линијом на два одвојена региона, који су идентификовани са + и -; б), регион формиран од много правих линија => неопходно развити више перцептроназаовајпроблем. b) 8/5
3 Реализација логичког ИЛИ w =, w =, w =, w =, w =, w = -, θ = 0.5, θ =.5, θ = /5
4 Вишеслојни перцептрони Проширују могућности класификације на шире скупове; Уводе се појмови хиперраван и хиперпростор, тако да су хиперравни, за n-димензионални простор (хиперпростор), одређене n- димензијом; У n-димензионалном улазном простору X, хиперраван H која врши сепарацију, дефинисана је на следећи начин: w x + wx + + wn xn = θ = w0 w x x Вектор тежинских односа w = [w,w,,w n ] Т управанна хиперраван; H + X X Каолинеарнисепаратор, перцептрон има велика ограничења у погледу нелинеарних пресликавања (бинарнаактивационафункција). 0/5
5 Backpropagation (BP) неуронска мрежа Развијена са циљем да се реши проблем нелинеарног пресликавања из улазног простора у излазни простор; Остварује се и модификација тежинских односа и између улазног и скривеног слоја неурона; Као и перцептрон, BP неуронска мрежа је мрежа са простирањем сигнала унапред; Реализује супервизорски вид учења; Користиградијентнипоступакприобучавању; Учипресликавањаизулазногпростораузоркауизлазнипростор, кроз процес минимизације грешке између актуелног излаза и захтеваног излаза; /5
6 Backpropagation (BP) неуронска мрежа Процес учења почиње са презентацијом улазног облика узорка BP мрежи; Простирањем кроз мрежу улазног облика узорка остварује се излазни облик; Затим се примењује генералисано делта правило да би се утврдила грешканаизлазу, којупростирањемуназадпрекоскривеногслоја, користи за лагано модификовање сваког тежинског односа између неурона; Поступак се понавља за сваки нови узорак; Систем BP неуронске мреже користи сигмоидну активациону функцију; Применом генералисаног делта правила утврђена грешка се коригује, тако што се користи први извод сигмоидне функције f (net)= f (S). Уколикосигмоиднафункција f(net) бржерасте, онда требаизвршитивећукорекцијугрешкеиобрнуто. /5
7 Архитектура BP мреже bias Елементарна архитектура BP мреже има три слоја; СлојевиСлојеви потпуноповезани; Користисеиструктураса више од једног скривеног слоја. I= [i,i, i,...,i R ] T улазни слој скривени слој излазни слој O=[o,o, o,...,o S ] T Број неурона у сваком слоју зависи од области примене, као и број скривених слојева; Најчешће постоји само један скривени слој, јер је BP мрежа са таквом структуром у стању да обезбеди репродуковање скупа захтеваних излазних облика за све обучавајуће парове; ЕкстраЕкстра улаз - неурон је увек активан и има излазно стање bias неурон; Понашасеумрежикаоисвакидругинеурон, иимазадатакдапартиципира у процесу учења побољшава конвергентне карактеристике BPмреже. /5
8 Генералисано делта правило Применом генералисаног делта правилa остварују се основне карактеристике мреже генерализација и нелинеарно раздвајање; M број обучавајућих парова, R број неурона у улазном слоју и С број неурона у излазном слоју; Обучавајућипарови (x,y )...(x М,y М ), којисудоведенина улаз мреже, обезбеђују мрежи могућност да реализује нелинеарнопресликавањеизмеђу x i и y i вектора, за i=,...,м. Lбројслојевамрежеинекајеса означенсвакислој: = 0 улазнислој, =,...,L скривенислој(еви), = L излазнислој. 4/5
9 Генералисано делта правило Неуронскамрежаима K неуронаусвакомслоју (гдеје =,...,L), Улазиуk-тинеурон -тогслојасудатипреко, зај=,...,k (истовременои излази неурона претходног слоја), који се могу означити са ; Сумирана улазна вредност за k-ти неурон у слоју је: S Излаз из k-тог неурона у -том слоју је остварен као резултат активације неурона; Преко функције преноса пропушта се улаз дат преко израза: K = net = O = f j= Грешка на излазном слоју L, BP неуронске мреже, је представљена разликом између израчунатих и задатих излаза: w kj ( S ) I + θ k O E pi = K L k= ( ) y O 5/5
10 Генералисано делта правило Минимизација грешке: = = K K E pi ( y O ) = y f k ( S ) k = k= ( ) =... = K K 0 0 K K y fk wkj f j + w ju fu w jvoiv + θ u + θ j θ k k = = = = j u v ГрадијентгрешкеЕ p, уодносунатежинскеодносе (заизлазнислој (=)): E w O I ( y O ) = ( y O ) f ( S ) I pi = k kj wkj Негативни предзнак указује на то да је правац промене тежинских односа са негативним градијентом Еp. 6/5
11 Генералисано делта правило ПравацпростирањаградијентагрешкеЕ p. Инкремент промене тежинских односа, за задати параметар учења η, је: i kj ( y O ) f ( S ) I η δ I w = η = k δ = ( y O ) f ( S ) k Параметар учења η се најчешће бира у опсегу од 0.5 (спорије обучавање) до 0.75 (брже, али нестабилније); Тежински односи се итеративно мењају док грешка Еp не оствари минумумутачки z min. Метода променљивог параметра:у почетку обучавања параметар η већи, током обучавања η се смањује, омогућавајући тако мрежи боље карактеристике учења. 7/5
12 Генералисано делта правило Други скривени слој (=): E w pi ju = K K O I I ( y ) ( ) ( ) ( ) O = y O f k S wkj f j S I iu k = i ju Први скривени слој (=): O O w ju Наосновуописаноггенералисаногделтаправила, алгоритамучења BP мрежеможесепредставитипрекоседамкорака, датихунаставку. k = w = ηδ I δ = f j ( S ) δ wkj E w = pi uv K ( y O ) K k = K K ( y O ) f k ( S ) wkj f j ( S ) w ju f u ( S iu ) x iv k= = k= O j= I O O O iu O iu iu w K iwuv = ηδ iu xiv δ iu = fu ( Siu ) δ w j= iu uv ju 8/5
13 Алгоритам учења BP неуронске мреже 9/5
14 Коришћене сигмоидне функције 0/5
15 E p Глобалнии локални минимуми z z min Понекад се обучавање BP неуронске мреже зауставља у тачки која се налази негде на правцу простирања градијента Еp, пре него што је стварни минимум остварен, јер је та вредност грешке Еp задовољавајућа. То управо говори о комплексности проблема конвергенције. z w Попречни пресек хипотетичке комплекснеповршигрешкее p у простору тежинских односа; Тачка z min јеглобални минимум. Каоштосевиди, наслициимаидругихтачака, z и z, којепредстављају локалне минимуме; Градијентни поступак минимизацијегрешкее p има зациљдасеуместоових локалних минимума пронађе глобални минимум. /5
16 Стохастички алгоритам тражења глобалног минимума E p w() w() w() w(0) w(6) w(7) w(8) w(9) w() w(5) w(4) w(0) w() w() Корисна хеуристичка техника напуштања тренутног локалног минимума и конвергирања ка дубљим локалним минимумима; Иницијализација алгоритма је у тачки w(0); w w w Трајекторија конвергенције се креће ка стриктном локалном минимуму који се налазиуw ; Након дивергенције до тачке w(), алгоритам враћа трајекторију конвергенције у w(4) уз тренутно задржавање у близини стриктног локалног минимума w; Следећа итерација: кретање ка тачки w(6); Обезбеђује секвенцијално конвергирање ка глобалном минимуму у w(0); /5
17 Стохастички алгоритам тражења глобалног минимума Бегом изстриктног глобалног минимума, преко тачака w() и w() (узевентуални одлазакиутачку w()), алгоритам остварује конвергенцију у стриктном глобалном минимуму w ; E p w() w() w() w(0) w(6) w(7) w(8) w(9) w() w(5) w(4) w(0) w() w() w w w У практичној примени алгоритам спорије конвергира ка глобалном минимуму; Свакиследећипутпроцесјезнатнобржи! Наградно питање: Да ли је брзина конвергенције важна за учење неуронске мреже? Одговор: Да, завећинупроблемавезанихзапроцесодлучивања, посебно када су роботи у питању! /5
18 Софтвер за симулирање вештачких неуронских мрежа- BPnet У BPnet-у је спроведена стохастичка конвергенција; Реализовано је рескалирање вредности улазних и излазних неурона каоињиховонормирање, причемусутевредностисведенена распон од 0. до 0.9, због успешне и брже стохастичке конвергенције; Када је конвергенција успешно завршена, вредностисеконвертују, рескалирањем у супротном смеру у стварне вредности (нпр. углова ротацијезазглобоверобота, З.Миљковић-књига); Конвергенција грешке Еp се прати и преко неколико контрола софтвера BPnet ( min. saved error ); Важну улогу у процесу конвергенције грешке Еp има и параметар учења η; Морадабудедовољномаликакоутоку тражења глобалног минимума или дубљег локалног минимума не би дошло до тога да мрежа веома тешко и споро пронађе уопште било какав прихватљив минимум грешке Еp; За конкретан проблем оптимална вредност параметра учења η је била 0.. 4/5
19 Хвалана напажњи! Питања? :: ИТС :: Вештачке неуронске мреже 5/5
Microsoft Word - III godina - EA - Metodi vjestacke inteligencije
 Школска година 2018/2019. Предмет Методи вјештачке интелигенције Шифра предмета 2284 Студијски програм Електроенергетика и аутоматика Циклус студија Година студија Семестар Број студената Број група за
Школска година 2018/2019. Предмет Методи вјештачке интелигенције Шифра предмета 2284 Студијски програм Електроенергетика и аутоматика Циклус студија Година студија Семестар Број студената Број група за
УНИВЕРЗИТЕТ У БЕОГРАДУ МАШИНСКИ ФАКУЛТЕТ Предмет: КОМПЈУТЕРСКА СИМУЛАЦИЈА И ВЕШТАЧКА ИНТЕЛИГЕНЦИЈА Задатак број: Лист/листова: 1/1 Задатак 5.1 Pостоје
 Лист/листова: 1/1 Задатак 5.1 Pостоје софтвери за препознавање бар кодова који знатно олакшавају велики број операција које захтевају препознавање објеката. Слика 1: Приказ свих слова за које је ART-1
Лист/листова: 1/1 Задатак 5.1 Pостоје софтвери за препознавање бар кодова који знатно олакшавају велики број операција које захтевају препознавање објеката. Слика 1: Приказ свих слова за које је ART-1
ПА-4 Машинско учење-алгоритми машинског учења
 ПА-4 Машинско учење-алгоритми машинског учења Машинско учење увод и основни појмови Деф: the desgn and development of algorthms that allow computers to mprove ther performance over tme based on data sensor
ПА-4 Машинско учење-алгоритми машинског учења Машинско учење увод и основни појмови Деф: the desgn and development of algorthms that allow computers to mprove ther performance over tme based on data sensor
I колоквијум из Основа рачунарске технике I СИ- 2017/2018 ( ) Р е ш е њ е Задатак 1 Тачка А Потребно је прво пронаћи вредности функција f(x
 I колоквијум из Основа рачунарске технике I СИ- / (...) Р е ш е њ е Задатак Тачка А Потребно је прво пронаћи вредности функција f(x, x, x ) и g(x, x, x ) на свим векторима. f(x, x, x ) = x x + x x + x
I колоквијум из Основа рачунарске технике I СИ- / (...) Р е ш е њ е Задатак Тачка А Потребно је прво пронаћи вредности функција f(x, x, x ) и g(x, x, x ) на свим векторима. f(x, x, x ) = x x + x x + x
P11.3 Analiza zivotnog veka, Graf smetnji
 Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
PowerPoint Presentation
 Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Microsoft Word - SIORT1_2019_K1_resenje.docx
 I колоквијум из Основа рачунарске технике I СИ- 208/209 (24.03.209.) Р е ш е њ е Задатак f(x, x 2, x 3 ) = (x + x x ) x (x x 2 + x ) + x x 2 x 3 f(x, x 2, x 3 ) = (x + x x ) (x x + (x )) 2 + x + x x 2
I колоквијум из Основа рачунарске технике I СИ- 208/209 (24.03.209.) Р е ш е њ е Задатак f(x, x 2, x 3 ) = (x + x x ) x (x x 2 + x ) + x x 2 x 3 f(x, x 2, x 3 ) = (x + x x ) (x x + (x )) 2 + x + x x 2
Optimizacija
 Optimizacija 1 / 43 2 / 43 Uvod u optimizaciju Zadana funkcija Uvod u optimizaciju f : R n R Cilj: Naći x, točku minimuma funkcije f : - Problem je jednostavno opisati x = arg min x R n f (x). - Rješavanje
Optimizacija 1 / 43 2 / 43 Uvod u optimizaciju Zadana funkcija Uvod u optimizaciju f : R n R Cilj: Naći x, točku minimuma funkcije f : - Problem je jednostavno opisati x = arg min x R n f (x). - Rješavanje
Newtonova metoda za rješavanje nelinearne jednadžbe f(x)=0
 za rješavanje nelinearne jednadžbe f (x) = 0 Ime Prezime 1, Ime Prezime 2 Odjel za matematiku Sveučilište u Osijeku Seminarski rad iz Matematičkog praktikuma Ime Prezime 1, Ime Prezime 2 za rješavanje
za rješavanje nelinearne jednadžbe f (x) = 0 Ime Prezime 1, Ime Prezime 2 Odjel za matematiku Sveučilište u Osijeku Seminarski rad iz Matematičkog praktikuma Ime Prezime 1, Ime Prezime 2 za rješavanje
Microsoft PowerPoint - Predavanje3.ppt
 Фрактална геометрија и фрактали у архитектури функционални системи Улаз Низ правила (функција F) Излаз Фрактална геометрија и фрактали у архитектури функционални системи Функционални систем: Улаз Низ правила
Фрактална геометрија и фрактали у архитектури функционални системи Улаз Низ правила (функција F) Излаз Фрактална геометрија и фрактали у архитектури функционални системи Функционални систем: Улаз Низ правила
Рачунарска интелигенција
 Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Орт колоквијум
 II колоквијум из Основа рачунарске технике I - 27/28 (.6.28.) Р е ш е њ е Задатак На улазе x, x 2, x 3, x 4 комбинационе мреже, са излазом z, долази четворобитни BCD број. Ако број са улаза при дељењу
II колоквијум из Основа рачунарске технике I - 27/28 (.6.28.) Р е ш е њ е Задатак На улазе x, x 2, x 3, x 4 комбинационе мреже, са излазом z, долази четворобитни BCD број. Ако број са улаза при дељењу
SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE ZAVRŠNI RAD Mario Svačina Zagreb, 2014.
 SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE ZAVRŠNI RAD Mario Svačina Zagreb, 2014. SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE ZAVRŠNI RAD Mentor: Prof. dr. sc. Dubravko Majetić
SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE ZAVRŠNI RAD Mario Svačina Zagreb, 2014. SVEUČILIŠTE U ZAGREBU FAKULTET STROJARSTVA I BRODOGRADNJE ZAVRŠNI RAD Mentor: Prof. dr. sc. Dubravko Majetić
ИНТЕЛИГЕНТНИ ТЕХНОЛОШКИ СИСТЕМИ АТ-6 Когнитивна роботика: Оцењивање положаја мобилног робота и карактеристичних објеката у технолошком окружењу Оцењив
 ИНТЕЛИГЕНТНИ ТЕХНОЛОШКИ СИСТЕМИ АТ-6 Когнитивна роботика: Оцењивање положаја мобилног робота и карактеристичних објеката у технолошком окружењу Оцењивање положаја робота и карактеристичних објеката у окружењу
ИНТЕЛИГЕНТНИ ТЕХНОЛОШКИ СИСТЕМИ АТ-6 Когнитивна роботика: Оцењивање положаја мобилног робота и карактеристичних објеката у технолошком окружењу Оцењивање положаја робота и карактеристичних објеката у окружењу
1
 Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Орт колоквијум
 I колоквијум из Основа рачунарске технике I - надокнада СИ - 008/009 (10.05.009.) Р е ш е њ е Задатак 1 a) Пошто постоје вектори на којима се функција f не јавља и вектори на којима има вредност један,
I колоквијум из Основа рачунарске технике I - надокнада СИ - 008/009 (10.05.009.) Р е ш е њ е Задатак 1 a) Пошто постоје вектори на којима се функција f не јавља и вектори на којима има вредност један,
PowerPoint Presentation
 Факултет организационих наука Центар за пословно одлучивање Системи за препоруку П8: Системи за препоруку Закључивање на основу случајева Системи за препоруку 2 Закључивање на основу случајева ПРОНАЂЕНО
Факултет организационих наука Центар за пословно одлучивање Системи за препоруку П8: Системи за препоруку Закључивање на основу случајева Системи за препоруку 2 Закључивање на основу случајева ПРОНАЂЕНО
Увод у организацију и архитектуру рачунара 1
 Увод у организацију и архитектуру рачунара 2 Александар Картељ kartelj@matf.bg.ac.rs Напомена: садржај ових слајдова је преузет од проф. Саше Малкова Увод у организацију и архитектуру рачунара 2 1 Секвенцијалне
Увод у организацију и архитектуру рачунара 2 Александар Картељ kartelj@matf.bg.ac.rs Напомена: садржај ових слајдова је преузет од проф. Саше Малкова Увод у организацију и архитектуру рачунара 2 1 Секвенцијалне
Microsoft PowerPoint - C-4-1
 Pregled iskaza u C-u Izraz; Iskaz dodele, serijski komponovani iskaz; blok Uslovni iskazi i izrazi; složeno grananje Iterativni iskazi Iskaz dodele Promena vrednosti a = Ψ; Izračunava vrednost izraza Ψ,
Pregled iskaza u C-u Izraz; Iskaz dodele, serijski komponovani iskaz; blok Uslovni iskazi i izrazi; složeno grananje Iterativni iskazi Iskaz dodele Promena vrednosti a = Ψ; Izračunava vrednost izraza Ψ,
Klasifikacija slika kucnih brojeva dubokim konvolucijskim modelima
 Klasifikacija slika kućnih brojeva dubokim konvolucijskim modelima Ivan Šego 4. srpnja 2018. Sadržaj 1 Uvod 2 Konvolucijske neuronske mreže Konvolucijski sloj Sloj sažimanja Potpuno povezani sloj 3 Ispitni
Klasifikacija slika kućnih brojeva dubokim konvolucijskim modelima Ivan Šego 4. srpnja 2018. Sadržaj 1 Uvod 2 Konvolucijske neuronske mreže Konvolucijski sloj Sloj sažimanja Potpuno povezani sloj 3 Ispitni
Slide 1
 Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
ELEKTROTEHNIČKI FAKULTET, UNIVERZITET U BEOGRADU KATEDRA ZA ELEKTRONIKU UVOD U ELEKTRONIKU - 13E041UE LABORATORIJSKA VEŽBA Primena mikrokontrolera
 ELEKTROTEHNIČKI FAKULTET, UNIVERZITET U BEOGRADU KATEDRA ZA ELEKTRONIKU UVOD U ELEKTRONIKU - 13E041UE LABORATORIJSKA VEŽBA Primena mikrokontrolera CILJ VEŽBE Cilj ove vežbe je da se studenti kreiranjem
ELEKTROTEHNIČKI FAKULTET, UNIVERZITET U BEOGRADU KATEDRA ZA ELEKTRONIKU UVOD U ELEKTRONIKU - 13E041UE LABORATORIJSKA VEŽBA Primena mikrokontrolera CILJ VEŽBE Cilj ove vežbe je da se studenti kreiranjem
Матрична анализа конструкција
 . 5 ПРИМЕР На слици. је приказан носач који је састављен од три штапа. Хоризонтални штапови су константног попречног пресека b/h=./.5 m, док је коси штап са линеарном променом висине. Одредити силе на
. 5 ПРИМЕР На слици. је приказан носач који је састављен од три штапа. Хоризонтални штапови су константног попречног пресека b/h=./.5 m, док је коси штап са линеарном променом висине. Одредити силе на
P9.1 Dodela resursa, Bojenje grafa
 Фаза доделе ресурса Ова фаза се у литератури назива и фазом доделе регистара, при чему се под регистрима подразумева скуп ресурса истог типа. Додела регистара променљивама из графа сметњи се обавља тзв.
Фаза доделе ресурса Ова фаза се у литератури назива и фазом доделе регистара, при чему се под регистрима подразумева скуп ресурса истог типа. Додела регистара променљивама из графа сметњи се обавља тзв.
Tutoring System for Distance Learning of Java Programming Language
 Deklaracija promenljivih Inicijalizacija promenljivih Deklaracija promenljive obuhvata: dodelu simboličkog imena promenljivoj i određivanje tipa promenljive (tip određuje koja će vrsta memorijskog registra
Deklaracija promenljivih Inicijalizacija promenljivih Deklaracija promenljive obuhvata: dodelu simboličkog imena promenljivoj i određivanje tipa promenljive (tip određuje koja će vrsta memorijskog registra
Verovatnoća - kolokvijum 17. decembar Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je
 Verovatnoća - kolokvijum 17. decembar 2016. 1. Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je 0.8. Ako je ispit težak, verovatnoća da se prvo pitanje
Verovatnoća - kolokvijum 17. decembar 2016. 1. Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je 0.8. Ako je ispit težak, verovatnoća da se prvo pitanje
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић
 Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Драган Пејић, Бојан Вујичић, Небојша Пјевалица,
Техничко решење: Метода мерења ефективне вредности сложенопериодичног сигнала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Драган Пејић, Бојан Вујичић, Небојша Пјевалица,
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA SEMINAR Duboke neuronske mreže Florijan Stamenković Voditelj: Marko Čupić Zagreb, ožujak 2
 SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA SEMINAR Duboke neuronske mreže Florijan Stamenković Voditelj: Marko Čupić Zagreb, ožujak 2015. SADRŽAJ 1. Uvod 1 2. Hopfieldove mreže 3 2.1.
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA SEMINAR Duboke neuronske mreže Florijan Stamenković Voditelj: Marko Čupić Zagreb, ožujak 2015. SADRŽAJ 1. Uvod 1 2. Hopfieldove mreže 3 2.1.
Орт колоквијум
 Задатак 1 I колоквијум из Основа рачунарске технике I - надокнада - 008/009 (16.05.009.) Р е ш е њ е a) Пошто постоје вектори на којима се функција f не јавља и вектори на којима има вредност један, лако
Задатак 1 I колоквијум из Основа рачунарске технике I - надокнада - 008/009 (16.05.009.) Р е ш е њ е a) Пошто постоје вектори на којима се функција f не јавља и вектори на којима има вредност један, лако
TEORIJA SIGNALA I INFORMACIJA
 Multiple Input/Multiple Output sistemi MIMO sistemi Ulazi (pobude) Izlazi (odzivi) u 1 u 2 y 1 y 2 u k y r Obrada=Matematički model Načini realizacije: fizički sistemi (hardware) i algoritmi (software)
Multiple Input/Multiple Output sistemi MIMO sistemi Ulazi (pobude) Izlazi (odzivi) u 1 u 2 y 1 y 2 u k y r Obrada=Matematički model Načini realizacije: fizički sistemi (hardware) i algoritmi (software)
Development Case
 Tehnička dokumentacija Verzija Studentski tim: Nastavnik: < izv. prof. dr. sc. Nikola Mišković> FER 2 -
Tehnička dokumentacija Verzija Studentski tim: Nastavnik: < izv. prof. dr. sc. Nikola Mišković> FER 2 -
1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan
 1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan jednačinom oblika: a 11 x 2 + 2a 12 xy + a 22 y 2
1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan jednačinom oblika: a 11 x 2 + 2a 12 xy + a 22 y 2
Programski jezik QBasic Kriteriji ocjenjivanja programiranje(b) - QBasic razred 42
 Kriteriji ocjenjivanja programiranje(b) - QBasic 5. - 8. razred 42 5. RAZRED - prisjeća sa pojmova: algoritam, algoritma slijeda i grananja, dijagrama toka, te ulaznih i izlaznih jedinica, ne shvaća njihovo
Kriteriji ocjenjivanja programiranje(b) - QBasic 5. - 8. razred 42 5. RAZRED - prisjeća sa pojmova: algoritam, algoritma slijeda i grananja, dijagrama toka, te ulaznih i izlaznih jedinica, ne shvaća njihovo
Programski jezik QBasic Kriteriji ocjenjivanja programiranje(b) - QBasic razred 42
 Kriteriji ocjenjivanja programiranje(b) - QBasic 5. - 8. razred 42 5. RAZRED - prisjeća sa pojmova: algoritam, algoritma slijeda i grananja, dijagrama toka, te ulaznih i izlaznih jedinica, ne shvaća njihovo
Kriteriji ocjenjivanja programiranje(b) - QBasic 5. - 8. razred 42 5. RAZRED - prisjeća sa pojmova: algoritam, algoritma slijeda i grananja, dijagrama toka, te ulaznih i izlaznih jedinica, ne shvaća njihovo
UNIVERZITET U BEOGRADU MATEMATIČKI FAKULTET MASTER RAD Iskazne neuronske mreže za aproksimaciju kombinatornih kola na osnovu uzorka ulaza i izlaza Stu
 UNIVERZITET U BEOGRADU MATEMATIČKI FAKULTET MASTER RAD Iskazne neuronske mreže za aproksimaciju kombinatornih kola na osnovu uzorka ulaza i izlaza Student: Marjana ŠOLAJIĆ Mentor: dr Mladen NIKOLIĆ Članovi
UNIVERZITET U BEOGRADU MATEMATIČKI FAKULTET MASTER RAD Iskazne neuronske mreže za aproksimaciju kombinatornih kola na osnovu uzorka ulaza i izlaza Student: Marjana ŠOLAJIĆ Mentor: dr Mladen NIKOLIĆ Članovi
POSLOVNI INFORMACIONI SISTEMI I RA^UNARSKE
 ZNAČAJ RAČUNARSKIH KOMUNIKACIJA U BANKARSKOM POSLOVANJU RAČUNARSKE MREŽE Računarske mreže su nastale kombinacijom računara i telekomunikacija dve tehnologije sa veoma različitom tradicijom i istorijom.
ZNAČAJ RAČUNARSKIH KOMUNIKACIJA U BANKARSKOM POSLOVANJU RAČUNARSKE MREŽE Računarske mreže su nastale kombinacijom računara i telekomunikacija dve tehnologije sa veoma različitom tradicijom i istorijom.
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br Autonomno kretanje virtualnih objekata Marin Hrkec Zagreb, lipanj 201
 SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br. 6404 Autonomno kretanje virtualnih objekata Marin Hrkec Zagreb, lipanj 2019. iii SADRŽAJ 1. Uvod 1 2. Korišteni alati i tehnologije
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br. 6404 Autonomno kretanje virtualnih objekata Marin Hrkec Zagreb, lipanj 2019. iii SADRŽAJ 1. Uvod 1 2. Korišteni alati i tehnologije
Техничко решење: Софтвер за симулацију стохастичког ортогоналног мерила сигнала, његовог интеграла и диференцијала Руководилац пројекта: Владимир Вуји
 Техничко решење: Софтвер за симулацију стохастичког ортогоналног мерила сигнала, његовог интеграла и диференцијала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Велибор
Техничко решење: Софтвер за симулацију стохастичког ортогоналног мерила сигнала, његовог интеграла и диференцијала Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Велибор
Орт колоквијум
 Испит из Основа рачунарске технике - / (6.6.. Р е ш е њ е Задатак Комбинациона мрежа има пет улаза, по два за број освојених сетова тенисера и један сигнал који одлучује ко је бољи уколико је резултат
Испит из Основа рачунарске технике - / (6.6.. Р е ш е њ е Задатак Комбинациона мрежа има пет улаза, по два за број освојених сетова тенисера и један сигнал који одлучује ко је бољи уколико је резултат
Classroom Expectations
 АТ-8: Терминирање производно-технолошких ентитета Проф. др Зоран Миљковић Садржај Пројектовање флексибилних ; Математички модел за оптимизацију флексибилних ; Генетички алгоритми у оптимизацији флексибилних
АТ-8: Терминирање производно-технолошких ентитета Проф. др Зоран Миљковић Садржај Пројектовање флексибилних ; Математички модел за оптимизацију флексибилних ; Генетички алгоритми у оптимизацији флексибилних
LAB PRAKTIKUM OR1 _ETR_
 UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA, TELEKOMUNIKACIJE I RAČUNARI PREDMET: OSNOVE RAČUNARSTVA 1 FOND ČASOVA: 2+1+1 LABORATORIJSKA VJEŽBA BROJ 1 NAZIV: REALIZACIJA
UNIVERZITET CRNE GORE ELEKTROTEHNIČKI FAKULTET STUDIJSKI PROGRAM: ELEKTRONIKA, TELEKOMUNIKACIJE I RAČUNARI PREDMET: OSNOVE RAČUNARSTVA 1 FOND ČASOVA: 2+1+1 LABORATORIJSKA VJEŽBA BROJ 1 NAZIV: REALIZACIJA
06 Poverljivost simetricnih algoritama1
 ЗАШТИТА ПОДАТАКА Симетрични алгоритми заштите поверљивост симетричних алгоритама Преглед биће објашњено: коришћење симетричних алгоритама заштите како би се заштитила поверљивост потреба за добрим системом
ЗАШТИТА ПОДАТАКА Симетрични алгоритми заштите поверљивост симетричних алгоритама Преглед биће објашњено: коришћење симетричних алгоритама заштите како би се заштитила поверљивост потреба за добрим системом
P3.2 Paralelno programiranje 2
 Paralelno programiranje II Analiza zavisnosti Struktura algoritma Pomoćne strukture Komunikacioni šabloni 1 4 Koraka paralelizacije programa 2 Evo algoritma. Gde je paralelizam? Dekompozicija zadataka
Paralelno programiranje II Analiza zavisnosti Struktura algoritma Pomoćne strukture Komunikacioni šabloni 1 4 Koraka paralelizacije programa 2 Evo algoritma. Gde je paralelizam? Dekompozicija zadataka
Matematka 1 Zadaci za vežbe Oktobar Uvod 1.1. Izračunati vrednost izraza (bez upotrebe pomoćnih sredstava): ( ) [ a) : b) 3 3
 Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
AKVIZICIJA PODATAKA SA UREĐAJEM NI USB-6008 NI USB-6008 je jednostavni višenamjenski uređaj koji se koristi za akviziciju podataka (preko USBa), kao i
 AKVIZICIJA PODATAKA SA UREĐAJEM NI USB-6008 NI USB-6008 je jednostavni višenamjenski uređaj koji se koristi za akviziciju podataka (preko USBa), kao i za generisanje željenih izlaznih signala (slika 1).
AKVIZICIJA PODATAKA SA UREĐAJEM NI USB-6008 NI USB-6008 je jednostavni višenamjenski uređaj koji se koristi za akviziciju podataka (preko USBa), kao i za generisanje željenih izlaznih signala (slika 1).
Microsoft PowerPoint - Topic02 - Serbian.ppt
 Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU FAKULTET ELEKTROTEHNIKE, RAČUNARSTVA I INFORMACIJSKIH TEHNOLOGIJA Sveučilišni preddiplomski studij PRI
 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU FAKULTET ELEKTROTEHNIKE, RAČUNARSTVA I INFORMACIJSKIH TEHNOLOGIJA Sveučilišni preddiplomski studij PRIMJENA STROJNOG UČENJA U KLASIFICIRANJU LEGO KOCAKA
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU FAKULTET ELEKTROTEHNIKE, RAČUNARSTVA I INFORMACIJSKIH TEHNOLOGIJA Sveučilišni preddiplomski studij PRIMJENA STROJNOG UČENJA U KLASIFICIRANJU LEGO KOCAKA
Vektorske funkcije i polja Mate Kosor / 23
 i polja Mate Kosor 9.12.2010. 1 / 23 Tokom vježbi pokušajte rješavati zadatke koji su vam zadani. Ova prezentacija biti će dostupna na webu. Isti format vježbi očekujte do kraja semestra. 2 / 23 Danas
i polja Mate Kosor 9.12.2010. 1 / 23 Tokom vježbi pokušajte rješavati zadatke koji su vam zadani. Ova prezentacija biti će dostupna na webu. Isti format vježbi očekujte do kraja semestra. 2 / 23 Danas
Projektovanje informacionih sistema i baze podataka
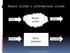 Realni sistem i informacioni sistem Ulaz Realni sistem Izlaz Unos Baza podataka Izveštaji Realni sistem i informacioni sistem Sistem se definiše kao skup objekata (entiteta) i njihovih međusobnih veza
Realni sistem i informacioni sistem Ulaz Realni sistem Izlaz Unos Baza podataka Izveštaji Realni sistem i informacioni sistem Sistem se definiše kao skup objekata (entiteta) i njihovih međusobnih veza
Microsoft PowerPoint - Topic02 - Serbian.ppt
 Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
Microsoft PowerPoint - DAC.ppt [Compatibility Mode]
![Microsoft PowerPoint - DAC.ppt [Compatibility Mode] Microsoft PowerPoint - DAC.ppt [Compatibility Mode]](/thumbs/100/145818915.jpg) Analogne i digitalne velicine Analogne veličine su kontinualne po vremenu i amplitudi. Digitalne veličine se predstavljaju nizom brojeva. Svaki broj predstavlja jedan odbirak u vremenu. Odbirak ima konačnu
Analogne i digitalne velicine Analogne veličine su kontinualne po vremenu i amplitudi. Digitalne veličine se predstavljaju nizom brojeva. Svaki broj predstavlja jedan odbirak u vremenu. Odbirak ima konačnu
Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]
![Microsoft PowerPoint - 03-Slozenost [Compatibility Mode] Microsoft PowerPoint - 03-Slozenost [Compatibility Mode]](/thumbs/102/154806426.jpg) Сложеност алгоритама (Програмирање 2, глава 3, глава 4-4.3) Проблем: класа задатака истог типа Велики број различитих (коректних) алгоритама Величина (димензија) проблема нпр. количина података које треба
Сложеност алгоритама (Програмирање 2, глава 3, глава 4-4.3) Проблем: класа задатака истог типа Велики број различитих (коректних) алгоритама Величина (димензија) проблема нпр. количина података које треба
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br Klasifikacija srčanih bolesti na temelju EKG signala uz pomoć strojno
 SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br. 4832 Klasifikacija srčanih bolesti na temelju EKG signala uz pomoć strojnog učenja podržanog evolucijskim računarstvom Danijel
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br. 4832 Klasifikacija srčanih bolesti na temelju EKG signala uz pomoć strojnog učenja podržanog evolucijskim računarstvom Danijel
3.Kontrlne (upravlja~ke) strukture u Javi
 Објектно орјентисано програмирање Владимир Филиповић vladaf@matf.bg.ac.rs Александар Картељ kartelj@matf.bg.ac.rs Низови у програмском језику Јава Владимир Филиповић vladaf@matf.bg.ac.rs Александар Картељ
Објектно орјентисано програмирање Владимир Филиповић vladaf@matf.bg.ac.rs Александар Картељ kartelj@matf.bg.ac.rs Низови у програмском језику Јава Владимир Филиповић vladaf@matf.bg.ac.rs Александар Картељ
Microsoft PowerPoint - 10 PEK EMT Logicka simulacija 1 od 2 (2012).ppt [Compatibility Mode]
![Microsoft PowerPoint - 10 PEK EMT Logicka simulacija 1 od 2 (2012).ppt [Compatibility Mode] Microsoft PowerPoint - 10 PEK EMT Logicka simulacija 1 od 2 (2012).ppt [Compatibility Mode]](/thumbs/101/150310241.jpg) ij Cilj: Dobiti što više informacija o ponašanju digitalnih kola za što kraće vreme. Metod: - Detaljni talasni oblik signala prikazati samo na nivou logičkih stanja. - Simulirati ponašanje kola samo u
ij Cilj: Dobiti što više informacija o ponašanju digitalnih kola za što kraće vreme. Metod: - Detaljni talasni oblik signala prikazati samo na nivou logičkih stanja. - Simulirati ponašanje kola samo u
2015_k2_z12.dvi
 OBLIKOVANJE I ANALIZA ALGORITAMA 2. kolokvij 27. 1. 2016. Skice rješenja prva dva zadatka 1. (20) Zadano je n poslova. Svaki posao je zadan kao vremenski interval realnih brojeva, P i = [p i,k i ],zai
OBLIKOVANJE I ANALIZA ALGORITAMA 2. kolokvij 27. 1. 2016. Skice rješenja prva dva zadatka 1. (20) Zadano je n poslova. Svaki posao je zadan kao vremenski interval realnih brojeva, P i = [p i,k i ],zai
РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена ) Прва година: ПРВА ГОДИНА - сви сем информатике Име пр
 РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена 23.01.2017.) Прва година: ПРВА ГОДИНА - сви сем информатике Име предмета Датум и термин одржавања писменог дела испита
РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена 23.01.2017.) Прва година: ПРВА ГОДИНА - сви сем информатике Име предмета Датум и термин одржавања писменог дела испита
Microsoft Word - Smerovi 1996
 ИСПИТНИ РОК: СЕПТЕМБАР 2018/2019 СТАРИ НАСТАВНИ ПЛАН И ПРОГРАМ (1996) Смер: СВИ Филозофија и социологија 20.08.2019 Теорија друштвеног развоја 20.08.2019 Програмирање 20.08.2019 Математика I 21.08.2019
ИСПИТНИ РОК: СЕПТЕМБАР 2018/2019 СТАРИ НАСТАВНИ ПЛАН И ПРОГРАМ (1996) Смер: СВИ Филозофија и социологија 20.08.2019 Теорија друштвеног развоја 20.08.2019 Програмирање 20.08.2019 Математика I 21.08.2019
Microsoft Word - ETH2_EM_Amperov i generalisani Amperov zakon - za sajt
 Полупречник унутрашњег проводника коаксијалног кабла је Спољашњи проводник је коначне дебљине унутрашњег полупречника и спољашњег Проводници кабла су начињени од бакра Кроз кабл протиче стална једносмерна
Полупречник унутрашњег проводника коаксијалног кабла је Спољашњи проводник је коначне дебљине унутрашњег полупречника и спољашњег Проводници кабла су начињени од бакра Кроз кабл протиче стална једносмерна
MIP-heuristike (Matheuristike) Hibridi izmedu metaheurističkih i egzaktnih metoda Tatjana Davidović Matematički institut SANU
 MIP-heuristike (Matheuristike) Hibridi izmedu metaheurističkih i egzaktnih metoda Tatjana Davidović Matematički institut SANU http://www.mi.sanu.ac.rs/ tanjad (tanjad@mi.sanu.ac.rs) 21. januar 2013. Tatjana
MIP-heuristike (Matheuristike) Hibridi izmedu metaheurističkih i egzaktnih metoda Tatjana Davidović Matematički institut SANU http://www.mi.sanu.ac.rs/ tanjad (tanjad@mi.sanu.ac.rs) 21. januar 2013. Tatjana
Numeričke metode u fizici 1, Projektni zadataci 2018./ Za sustav običnih diferencijalnih jednadžbi, koje opisuju kretanje populacije dviju vrs
 Numeričke metode u fizici, Projektni zadataci 8./9.. Za sustav običnih diferencijalnih jednadžbi, koje opisuju kretanje populacije dviju vrsta životinja koje se nadmeću za istu hranu, dx ( dt = x x ) xy
Numeričke metode u fizici, Projektni zadataci 8./9.. Za sustav običnih diferencijalnih jednadžbi, koje opisuju kretanje populacije dviju vrsta životinja koje se nadmeću za istu hranu, dx ( dt = x x ) xy
Slide 1
 Универзитет у Београду Машински факултет Катедра за производно машинство ЕМПИРИЈСКО УПРАВЉАЊЕ ИНТЕЛИГЕНТНОГ МОБИЛНОГ РОБОТА БАЗИРАНО НА МАШИНСКОМ УЧЕЊУ Кандидат: Марко Митић, дипл. маш. инж. Комисија за
Универзитет у Београду Машински факултет Катедра за производно машинство ЕМПИРИЈСКО УПРАВЉАЊЕ ИНТЕЛИГЕНТНОГ МОБИЛНОГ РОБОТА БАЗИРАНО НА МАШИНСКОМ УЧЕЊУ Кандидат: Марко Митић, дипл. маш. инж. Комисија за
СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за векто
![СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за векто СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за векто](/thumbs/102/155791469.jpg) СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за вектор a (коjи може бити и дужине нула) и неке изометриjе
СТРАХИЊА РАДИЋ КЛАСИФИКАЦИJА ИЗОМЕТРИJА И СЛИЧНОСТИ Према књизи [1], свака изометриjа σ се може представити ком позици - jом неке транслациjе за вектор a (коjи може бити и дужине нула) и неке изометриjе
Napredno estimiranje strukture i gibanja kalibriranim parom kamera
 Napredno estimiranje strukture i gibanja kalibriranim parom kamera Ivan Krešo Mentor: Siniša Šegvić 3. srpnja 2013. Motivacija Stereo vid dvije kamere omogućavaju mjerenje dubine korespondentnih točaka
Napredno estimiranje strukture i gibanja kalibriranim parom kamera Ivan Krešo Mentor: Siniša Šegvić 3. srpnja 2013. Motivacija Stereo vid dvije kamere omogućavaju mjerenje dubine korespondentnih točaka
Odreivanje neodreenosti hadronske strukture metodama strojnog ucenja
 Odredivanje neodredenosti hadronske strukture metodama strojnog učenja Ivan Ćorić 1 Mentor: prof. Krešimir Kumerički 1 1 Prirodoslovno matematički fakultet, Fizički odsjek Sveučilište u Zagrebu 29. siječnja
Odredivanje neodredenosti hadronske strukture metodama strojnog učenja Ivan Ćorić 1 Mentor: prof. Krešimir Kumerički 1 1 Prirodoslovno matematički fakultet, Fizički odsjek Sveučilište u Zagrebu 29. siječnja
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br PREDVIÐANJE POTROŠNJE ELEKTRIČNE ENERGIJE NA SVEUČILIŠTU U ZAGREBU FA
 SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br. 2500 PREDVIÐANJE POTROŠNJE ELEKTRIČNE ENERGIJE NA SVEUČILIŠTU U ZAGREBU FAKULTETU ELEKTROTEHNIKE I RAČUNARSTVA NEURONSKOM MREŽOM
SVEUČILIŠTE U ZAGREBU FAKULTET ELEKTROTEHNIKE I RAČUNARSTVA ZAVRŠNI RAD br. 2500 PREDVIÐANJE POTROŠNJE ELEKTRIČNE ENERGIJE NA SVEUČILIŠTU U ZAGREBU FAKULTETU ELEKTROTEHNIKE I RAČUNARSTVA NEURONSKOM MREŽOM
Microsoft PowerPoint - OOPpredavanja05 [Compatibility Mode]
![Microsoft PowerPoint - OOPpredavanja05 [Compatibility Mode] Microsoft PowerPoint - OOPpredavanja05 [Compatibility Mode]](/thumbs/88/116292779.jpg) OBJEKTNO ORIJENTISANO PROGRAMIRANJE PREDAVANJE 5 OBJEKTI U INTERAKCIJI Miloš Kovačević Đorđe Nedeljković 1 /25 OSNOVNI KONCEPTI - Abstrakcija - Modularizacija - Objektne reference - Klasni dijagram - Objektni
OBJEKTNO ORIJENTISANO PROGRAMIRANJE PREDAVANJE 5 OBJEKTI U INTERAKCIJI Miloš Kovačević Đorđe Nedeljković 1 /25 OSNOVNI KONCEPTI - Abstrakcija - Modularizacija - Objektne reference - Klasni dijagram - Objektni
ТЕОРИЈА УЗОРАКА 2
 ТЕОРИЈА УЗОРАКА 2 12. 04. 13. ВЕЖБАЊА Написати функције за бирање елемената популације обима N у узорак обима n, код простог случајног узорка, користећи алгоритме: Draw by draw procedure for SRS/SRSWOR
ТЕОРИЈА УЗОРАКА 2 12. 04. 13. ВЕЖБАЊА Написати функције за бирање елемената популације обима N у узорак обима n, код простог случајног узорка, користећи алгоритме: Draw by draw procedure for SRS/SRSWOR
DUBINSKA ANALIZA PODATAKA
 DUBINSKA ANALIZA PODATAKA () ASOCIJACIJSKA PRAVILA (ENGL. ASSOCIATION RULE) Studeni 2018. Mario Somek SADRŽAJ Asocijacijska pravila? Oblici učenja pravila Podaci za analizu Algoritam Primjer Izvođenje
DUBINSKA ANALIZA PODATAKA () ASOCIJACIJSKA PRAVILA (ENGL. ASSOCIATION RULE) Studeni 2018. Mario Somek SADRŽAJ Asocijacijska pravila? Oblici učenja pravila Podaci za analizu Algoritam Primjer Izvođenje
Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odr
 Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odrediti njene krajeve. b) Odrediti sledeće skupove: -
Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odrediti njene krajeve. b) Odrediti sledeće skupove: -
DISKRETNA MATEMATIKA
 DISKRETNA MATEMATIKA Kombinatorika Permutacije, kombinacije, varijacije, binomna formula Ivana Milosavljević - 1 - 1. KOMBINATORIKA PRINCIPI PREBROJAVANJA Predmet kombinatorike je raspoređivanje elemenata
DISKRETNA MATEMATIKA Kombinatorika Permutacije, kombinacije, varijacije, binomna formula Ivana Milosavljević - 1 - 1. KOMBINATORIKA PRINCIPI PREBROJAVANJA Predmet kombinatorike je raspoređivanje elemenata
Mere slicnosti
 Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
ЛИНЕАРНА ФУНКЦИЈА ЛИНЕАРНА ФУНКЦИЈА у = kх + n А утврди 1. Које од наведених функција су линеарне: а) у = 2х; б) у = 4х; в) у = 2х 7; г) у = 2 5 x; д)
 ЛИНЕАРНА ФУНКЦИЈА ЛИНЕАРНА ФУНКЦИЈА у = kх + n А утврди 1. Које од наведених функција су линеарне: а) у = х; б) у = 4х; в) у = х 7; г) у = 5 x; д) у = 5x ; ђ) у = х + х; е) у = x + 5; ж) у = 5 x ; з) у
ЛИНЕАРНА ФУНКЦИЈА ЛИНЕАРНА ФУНКЦИЈА у = kх + n А утврди 1. Које од наведених функција су линеарне: а) у = х; б) у = 4х; в) у = х 7; г) у = 5 x; д) у = 5x ; ђ) у = х + х; е) у = x + 5; ж) у = 5 x ; з) у
I година Назив предмета I термин Вријеме II термин Вријеме Сала Математика : :00 све Основи електротехнике
 I година Математика 1 2225 07.02.2019. 9:00 21.02.2019. 9:00 све Основи електротехнике 1 2226 04.02.2019. 9:00 18.02.2019. 9:00 све Програмирање 1 2227 08.02.2019. 9:00 22.02.2019. 9:00 све Основи рачунарске
I година Математика 1 2225 07.02.2019. 9:00 21.02.2019. 9:00 све Основи електротехнике 1 2226 04.02.2019. 9:00 18.02.2019. 9:00 све Програмирање 1 2227 08.02.2019. 9:00 22.02.2019. 9:00 све Основи рачунарске
I година Назив предмета I термин Вријеме II термин Вријеме Сала Математика : :00 све Основи електротехнике
 I година Математика 1 2225 20.06.2019. 9:00 04.07.2019. 9:00 све Основи електротехнике 1 2226 17.06.2019. 9:00 01.07.2019. 13:00 све Програмирање 1 2227 21.06.2019. 9:00 05.07.2019. 9:00 све Основи рачунарске
I година Математика 1 2225 20.06.2019. 9:00 04.07.2019. 9:00 све Основи електротехнике 1 2226 17.06.2019. 9:00 01.07.2019. 13:00 све Програмирање 1 2227 21.06.2019. 9:00 05.07.2019. 9:00 све Основи рачунарске
I година Назив предмета I термин Вријеме II термин Вријеме Сала Математика : :00 све Основи електротехнике
 I година Математика 1 2225 05.09.2019. 9:00 19.09.2019. 9:00 све Основи електротехнике 1 2226 02.09.2019. 9:00 16.09.2019. 9:00 све Програмирање 1 2227 06.09.2019. 9:00 20.09.2019. 9:00 све Основи рачунарске
I година Математика 1 2225 05.09.2019. 9:00 19.09.2019. 9:00 све Основи електротехнике 1 2226 02.09.2019. 9:00 16.09.2019. 9:00 све Програмирање 1 2227 06.09.2019. 9:00 20.09.2019. 9:00 све Основи рачунарске
PowerPoint Presentation
 НАПРЕДНО ПЛАНИРАЊЕ И РАСПОРЕЂИВАЊЕ Милан Станојевић, Гордана Савић, Драгана Макајић-Николић Начин полагања испита Студије случаја Задате Изабране самостално Направљен систем за подршку одлучивању у проблему
НАПРЕДНО ПЛАНИРАЊЕ И РАСПОРЕЂИВАЊЕ Милан Станојевић, Гордана Савић, Драгана Макајић-Николић Начин полагања испита Студије случаја Задате Изабране самостално Направљен систем за подршку одлучивању у проблему
Slide 1
 Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 1: Увод и историјски развој теорије система UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES Катедра за управљање системима Наставници:
Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 1: Увод и историјски развој теорије система UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES Катедра за управљање системима Наставници:
PLAN I PROGRAM ZA DOPUNSKU (PRODUŽNU) NASTAVU IZ MATEMATIKE (za 1. razred)
 PLAN I PROGRAM ZA DOPUNSKU (PRODUŽNU) NASTAVU IZ MATEMATIKE (za 1. razred) Učenik prvog razreda treba ostvarit sljedeće minimalne standarde 1. SKUP REALNIH BROJEVA -razlikovati brojevne skupove i njihove
PLAN I PROGRAM ZA DOPUNSKU (PRODUŽNU) NASTAVU IZ MATEMATIKE (za 1. razred) Učenik prvog razreda treba ostvarit sljedeće minimalne standarde 1. SKUP REALNIH BROJEVA -razlikovati brojevne skupove i njihove
untitled
 С А Д Р Ж А Ј Предговор...1 I II ОСНОВНИ ПОЈМОВИ И ДЕФИНИЦИЈЕ...3 1. Предмет и метод термодинамике... 3 2. Термодинамички систем... 4 3. Величине (параметри) стања... 6 3.1. Специфична запремина и густина...
С А Д Р Ж А Ј Предговор...1 I II ОСНОВНИ ПОЈМОВИ И ДЕФИНИЦИЈЕ...3 1. Предмет и метод термодинамике... 3 2. Термодинамички систем... 4 3. Величине (параметри) стања... 6 3.1. Специфична запремина и густина...
I година Назив предмета I термин Вријеме Сала Математика :00 све Основи електротехнике :00 све Програмирање
 I година Математика 1 2225 03.10.2019. 15:00 све Основи електротехнике 1 2226 30.09.2019. 15:00 све Програмирање 1 2227 04.10.2019. 15:00 све Основи рачунарске технике 2228 01.10.2019. 15:00 све Социологија
I година Математика 1 2225 03.10.2019. 15:00 све Основи електротехнике 1 2226 30.09.2019. 15:00 све Програмирање 1 2227 04.10.2019. 15:00 све Основи рачунарске технике 2228 01.10.2019. 15:00 све Социологија
9. : , ( )
 9. Динамика тачке: Енергиjа, рад и снага (први део) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj - Шта ћемо научити (1) 1. Преглед литературе
9. Динамика тачке: Енергиjа, рад и снага (први део) др Ратко Маретић др Дамир Мађаревић Департман за Техничку механику, Факултет техничких наука Нови Сад Садржаj - Шта ћемо научити (1) 1. Преглед литературе
Microsoft PowerPoint - 3_Elektrohemijska_korozija_kinetika.ppt - Compatibility Mode
 KOROZIJA I ZAŠTITA METALA dr Aleksandar Lj. Bojić Elektrohemijska korozija Kinetika korozionog procesa 1 Korozioni sistem izvan stanja ravnoteže polarizacija Korozija metala: istovremeno odvijanje dve
KOROZIJA I ZAŠTITA METALA dr Aleksandar Lj. Bojić Elektrohemijska korozija Kinetika korozionog procesa 1 Korozioni sistem izvan stanja ravnoteže polarizacija Korozija metala: istovremeno odvijanje dve
Slide 1
 Mjerenja kvaliteta servisa mobilnih mreža u Crnoj Gori Ivan Vujović menadžer za kontrolu i monitoring RF spektra 1 Radio-frekvencijskim spektrom, kao ograničenim prirodnim resursom države Crne Gore, upravlja
Mjerenja kvaliteta servisa mobilnih mreža u Crnoj Gori Ivan Vujović menadžer za kontrolu i monitoring RF spektra 1 Radio-frekvencijskim spektrom, kao ograničenim prirodnim resursom države Crne Gore, upravlja
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аут
 Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Иван Жупунски, Небојша Пјевалица, Марјан Урекар,
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Иван Жупунски, Небојша Пјевалица, Марјан Урекар,
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe
 6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe, očekuje se da su koordinate celobrojne. U slučaju
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe, očekuje se da su koordinate celobrojne. U slučaju
1 MATEMATIKA 1 (prva zadaća) Vektori i primjene 1. U trokutu ABC točke M i N dijele stranicu AB na tri jednaka dijela. O
 http://www.fsb.hr/matematika/ (prva zadać Vektori i primjene. U trokutu ABC točke M i N dijele stranicu AB na tri jednaka dijela. Označite CA= a, CB= b i izrazite vektore CM i CN pomoću vektora a i b..
http://www.fsb.hr/matematika/ (prva zadać Vektori i primjene. U trokutu ABC točke M i N dijele stranicu AB na tri jednaka dijela. Označite CA= a, CB= b i izrazite vektore CM i CN pomoću vektora a i b..
UDŽBENIK 2. dio
 UDŽBENIK 2. dio Pročitaj pažljivo Primjer 1. i Primjer 2. Ova dva primjera bi te trebala uvjeriti u potrebu za uvo - denjem još jedne vrste brojeva. Primjer 1. Živa u termometru pokazivala je temperaturu
UDŽBENIK 2. dio Pročitaj pažljivo Primjer 1. i Primjer 2. Ova dva primjera bi te trebala uvjeriti u potrebu za uvo - denjem još jedne vrste brojeva. Primjer 1. Živa u termometru pokazivala je temperaturu
Betonske i zidane konstrukcije 2
 5. STTIČKI PRORČUN PLOČE KRKTERISTIČNOG KT PROGR IZ KOLEGIJ BETONSKE I ZIDNE KONSTRUKCIJE 44 15 4 4 5. Statički proračun ploče karakterističnog kata 5.1. naliza opterećenja Stambeni prostor: 15 4 5, parket
5. STTIČKI PRORČUN PLOČE KRKTERISTIČNOG KT PROGR IZ KOLEGIJ BETONSKE I ZIDNE KONSTRUKCIJE 44 15 4 4 5. Statički proračun ploče karakterističnog kata 5.1. naliza opterećenja Stambeni prostor: 15 4 5, parket
Microsoft Word - Dopunski_zadaci_iz_MFII_uz_III_kolokvij.doc
 Dopunski zadaci za vježbu iz MFII Za treći kolokvij 1. U paralelno strujanje fluida gustoće ρ = 999.8 kg/m viskoznosti μ = 1.1 1 Pa s brzinom v = 1.6 m/s postavljana je ravna ploča duljine =.7 m (u smjeru
Dopunski zadaci za vježbu iz MFII Za treći kolokvij 1. U paralelno strujanje fluida gustoće ρ = 999.8 kg/m viskoznosti μ = 1.1 1 Pa s brzinom v = 1.6 m/s postavljana je ravna ploča duljine =.7 m (u smjeru
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica
 Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
Algoritmi i arhitekture DSP I
 Univerzitet u Novom Sadu Fakultet Tehničkih Nauka Katedra za računarsku tehniku i međuračunarske komunikacije Algoritmi i arhitekture DSP I INTERNA ORGANIACIJA DIGITALNOG PROCESORA A OBRADU SIGNALA INTERNA
Univerzitet u Novom Sadu Fakultet Tehničkih Nauka Katedra za računarsku tehniku i međuračunarske komunikacije Algoritmi i arhitekture DSP I INTERNA ORGANIACIJA DIGITALNOG PROCESORA A OBRADU SIGNALA INTERNA
Postavka 2: Osnovni graf algoritmi 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch
 Postavka 2: Osnovni graf algoritmi 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch A1 Slanje svima preko fiksiranog razapinjućeg stabla
Postavka 2: Osnovni graf algoritmi 1 DISTRIBUIRANI ALGORITMI I SISTEMI Iz kursa CSCE 668 Proleće 2014 Autor izvorne prezentacije: Prof. Jennifer Welch A1 Slanje svima preko fiksiranog razapinjućeg stabla
Uvod u statistiku
 Uvod u statistiku Osnovni pojmovi Statistika nauka o podacima Uključuje prikupljanje, klasifikaciju, prikaz, obradu i interpretaciju podataka Staistička jedinica objekat kome se mjeri neko svojstvo. Svi
Uvod u statistiku Osnovni pojmovi Statistika nauka o podacima Uključuje prikupljanje, klasifikaciju, prikaz, obradu i interpretaciju podataka Staistička jedinica objekat kome se mjeri neko svojstvo. Svi
АНКЕТА О ИЗБОРУ СТУДИЈСКИХ ГРУПА И МОДУЛА СТУДИЈСКИ ПРОГРАМИ МАСТЕР АКАДЕМСКИХ СТУДИЈА (МАС): А) РАЧУНАРСТВО И АУТОМАТИКА (РиА) и Б) СОФТВЕРСКО ИНЖЕЊЕ
 АНКЕТА О ИЗБОРУ СТУДИЈСКИХ ГРУПА И МОДУЛА СТУДИЈСКИ ПРОГРАМИ МАСТЕР АКАДЕМСКИХ СТУДИЈА (МАС): А) РАЧУНАРСТВО И АУТОМАТИКА (РиА) и Б) СОФТВЕРСКО ИНЖЕЊЕРСТВО И ИНФОРМАЦИОНЕ ТЕХНОЛОГИЈЕ (СИИТ) У циљу бољег
АНКЕТА О ИЗБОРУ СТУДИЈСКИХ ГРУПА И МОДУЛА СТУДИЈСКИ ПРОГРАМИ МАСТЕР АКАДЕМСКИХ СТУДИЈА (МАС): А) РАЧУНАРСТВО И АУТОМАТИКА (РиА) и Б) СОФТВЕРСКО ИНЖЕЊЕРСТВО И ИНФОРМАЦИОНЕ ТЕХНОЛОГИЈЕ (СИИТ) У циљу бољег
KATALOG ZNANJA IZ INFORMATIKE
 KATALOG ZNANJA IZ INFORMATIKE Nacionalni savjet za obrazovanje je na 27. sjednici održanoj 17. marta 2014. godine utvrdio izmjene predmetnoga programa INFORMATIKA za I razred gimnazije. Na zahtijev Pedagoško-psihološke
KATALOG ZNANJA IZ INFORMATIKE Nacionalni savjet za obrazovanje je na 27. sjednici održanoj 17. marta 2014. godine utvrdio izmjene predmetnoga programa INFORMATIKA za I razred gimnazije. Na zahtijev Pedagoško-psihološke
P1.0 Uvod
 Системска програмска подршка у реалном времену 1 Миодраг Ђукић miodrag.djukic@rt-rk.uns.ac.rs www.rt-rk.uns.ac.rs 1 Системска програмска подршка у реалном времену 1 програмска подршка = софтвер Системски
Системска програмска подршка у реалном времену 1 Миодраг Ђукић miodrag.djukic@rt-rk.uns.ac.rs www.rt-rk.uns.ac.rs 1 Системска програмска подршка у реалном времену 1 програмска подршка = софтвер Системски
PowerPoint Presentation
 Data mining kocepti i tehnike Udžbenik: Data Mining: Concepts and Techniques, Jiawei Han, Micheline Kamber Introduction to Data Mining, Pang-Ning Tan, Michael Steinbach, Vipin Kumar Ocjenjivanje: kolokvijumi
Data mining kocepti i tehnike Udžbenik: Data Mining: Concepts and Techniques, Jiawei Han, Micheline Kamber Introduction to Data Mining, Pang-Ning Tan, Michael Steinbach, Vipin Kumar Ocjenjivanje: kolokvijumi
Microsoft PowerPoint - 13-Funkcije_2.ppt [Compatibility Mode]
![Microsoft PowerPoint - 13-Funkcije_2.ppt [Compatibility Mode] Microsoft PowerPoint - 13-Funkcije_2.ppt [Compatibility Mode]](/thumbs/100/145658154.jpg) Osnove programiranja Funkcije - Metode Prenos parametara Po vrednosti Po referenci Po izlazu Sadržaj Opseg važenja promenljive u drugim strukturama Rekurzije Prenos parametara Metoda može vratiti isključivo
Osnove programiranja Funkcije - Metode Prenos parametara Po vrednosti Po referenci Po izlazu Sadržaj Opseg važenja promenljive u drugim strukturama Rekurzije Prenos parametara Metoda može vratiti isključivo
УНИВЕРЗИТЕТ У НОВОМ САДУ ОБРАЗАЦ 6
 УНИВЕРЗИТЕТ У НОВОМ САДУ ОБРАЗАЦ 6. ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА ИЗВЕШТАЈ О ОЦЕНИ ДОКТОРСКЕ ДИСЕРТАЦИЈЕ Мр БОШКА БОЖИЛОВИЋА I ПОДАЦИ О КОМИСИЈИ 1. Датум и орган који је именовао комисију Решење Декана Факултета
УНИВЕРЗИТЕТ У НОВОМ САДУ ОБРАЗАЦ 6. ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА ИЗВЕШТАЈ О ОЦЕНИ ДОКТОРСКЕ ДИСЕРТАЦИЈЕ Мр БОШКА БОЖИЛОВИЋА I ПОДАЦИ О КОМИСИЈИ 1. Датум и орган који је именовао комисију Решење Декана Факултета
