samo NASLOV8_Layout 1
|
|
|
- Tomaž Slokar
- пре 6 година
- Прикази:
Транскрипт
1 UDC: : PREGLEDNI RAD PRIMENA FAZI TEORIJE U IZRADI DINAMIČKIH PLANOVA GRAĐENJA PO METODI KRITIČNOG PUTA APPLICATION OF FAZZY CRITICAL PATH METHOD TO CONSTRUCTION PLANING Prof. Dr Kazimir Kurij, dipl. inž. Mr Saša Jovanović, dipl. inž. građ. Fakultet za graditeljski menadžment, Beograd SAŽETAK Ovaj rad prikazuje jednu od metoda za izradu dinamičkih planova u graditeljstvu, u uslovima neizvesnosti, baziranu na fazi teoriji. Namena metode kritičnog puta (CPM) je da identifikuje kritične aktivnosti i kritične puteve u mrežnom dijagramu, koji grafičiki prikazuje dinamički plan izgradnje objekta. Međutim u praksi je najčeši slučaj da se trajanje aktivnosti u dinamičkom planu procenjuje na osnovu intuicije, odnosno profesionalnog osećanja pojedinaca, što se može pretpostaviti da je neprecizno i ne pouzdano. Korišćenje nepreciznih podataka o trajanju aktivnosti u graditeljstvu zahteva i odgovarajuće metode analize vremena u mrežnom dijagramu, kao što je koncept fazifikacije, gde se nesigurnost procene trajanja aktivnosti prikazuje u vidu fazi broja. Ovaj rad prikazuje metodu definisanja fazi kritičnog puta u kojem su aktivnosti predstavljene trapezoidnim fazi brojevima. Ključne reči: Kritični put, trapezoidni fazi brojevi, fazi CPM, fazi projekt, nepreciznost. ABSTRACT This paper presents a method based on fuzzy theory for solving fazzy project planing in fuzy enviroment. The purpose of the critical path method (CPM) is to identify the critical activities in the critical path of an activity network. However, in the real world for many project it has to use human judgment for estimating the duration of activities and it has supposed duration of acitivities are very imprecise. A way to deal with this imprecise data is to employ te concept of fuzzines, where the vague activity times can be represents by fuzzy sets. This paper prezents a method for finding critical path in the fuzzy project network. Trapezoidal fuzzy numbers are used to represents activity times in the project network. Key words: Critical Path Method, trapezoidal fuzzy numbers, fazzy projects, fuzzy CPM, imprecise. 1. UVOD Pouzdanost dinamičkih planova u graditeljstvu uglavnom zavisi od detaljnosti i tačnosti analize strukture plana i preciznosti podataka o vremenu trajanja aktivnosti u mrežnom planu. Dok se problem analize strukture plana može rešiti angažovanjem izuzetnih stručnjaka tehnologa za određenu oblast graditeljstva, nepreciznost vremena trajanja aktivnosti ostaje i dalje problem koji ugrožava pouzdanost dinamičkog plana. Trajanje aktivnosti u graditeljstvu uglavnom se određuje na osnovu zvaničnih normativa, ali kada se uzme u obzir definicija normativa koja glasi: Normativ je vreme potrebno kvalifikovanom (obučenom) radniku, odgovarajuće struke, da po određenom postupku i redosledu radnih operacija, određenom vrstom materijala, određenim alatima i mašinama, u normalnim uslovima okruženja, uz normalno zalaganje i zamor izvrši tačno određen posao, [4] Lako se dolazi do zaključka da izmena bilo kog parametra iz definicije normativa (obučenost, postupak, alat, mašne, uslovi na radnom mestu, zalaganje, zamor i sl.) dovodi i do promene vrednosti normativa. To znači da za jednu aktivnost normativ, nije jedan broj, nego čitav spektar brojeva, zavisno od promenljivih parametara u definiciji normativa. TEHNIČKA DIJAGNOSTIKA (BROJ ) 59
2 Uzimajući u obzir da još uvek nema zvaničnih normativa dobivenih naučno istaživačkm pristupom, čija bi vrednost, u skladu sa definicijom normativa, bila izražena nekom srednjom vrednosti i odgovarajućim intervalom poverenja izraženim standardnom devijacijom, fazi logika i fazi skupovi mogu da budu pravo rešenje za rešavanje nepreciznosti dinamičkih planova u graditeljstvu. Fazi logika i fazi skupovi, kao nov pojam definisani su još godine (Lotfi Zadeh), sa osnovnim ciljem da se na matematički formalizovan način predtstavi i modelira nepreciznost, odnosno neodređenost u ljudskom razmišljanju i subjektivnosti. Fazi logika je našla veliku primenu u teoriji upravljanja, kvantitativnoj analizi, informacionim sistemima planiranje itd, odnosno u svim slučajevima gde ne postoji matematički model ili je isti suviše kompleksan za rad u praksi. Za razliku od diskretnih skupova gde element ili pripada ili ne pripada određenom skupu, što se matematički kaže da je stepen pripadnosti skupu 1 (ako pripada) ili 0 (ako ne pripada), elementi u fuzzy skupovima mogu da pripadaju skupu, delimično da pripadaju skupu ili uopšte ne pripadaju skupu, što se matematički može izraziti kao broj 1 (100% pripada skupu), broj 0.7 (70% pripada skupu i broj 0 (uopšte ne pripada skupu). Ovim pristupom mogu se preciznije da reprezentuju neprecizni iskazi. Na primer, da li je jasna granica između skupova mlad čovek i star čovek. Neka je za jasan, klasičan skup granica npr. 50 godina Sl.1, (isprekidana linija). Međutim očito je da je percepcija pojma star svakog pojedinca različita. Ako se prihvati da ljudi mlađi od 25 godina definitivno ne pripadaju skupu Star čovek, tj. pripadaju mu sa stepenom 0, a da stepen pripadnosti skupu Star čovek raste u intervalu od 25 do 75 godina, pri čemu se ljudi stariji od 75 godina definitivno smatraju starim (stepen pripadnosti je jednak 1), definicija skupa Star čovek može se prikazati monotono neopadajućom funkcijom pripadnosti: Sl.1. (kriva puna linija). Potpuno je jasno da je ovakvo preslikavanje ulaznih promenjivih (godine) u odgovarajuće vrednosti funkcije pripadnosti fazi skupa Star čovek mnogo bliže ljudskom načinu razmišljanja nego li slučaj preslikavanja koje definiše jasne skupove. [5] Cilj ovog rada je da ukaže na realnu primenljivost fazi brojeva kod izražavanja trajanja aktivnosti u graditeljskim dinamičkim planovima. Radi toga urađen je jedan primer sa malim brojem aktivnosti u mrežnom dijagramu, ali sa detaljno razrađenim algoritmom postupka iznalaženja kritičnog puta. Za dati primer urađen je i odgovarajući algoritam rešenja problema (t. 2.1). 60 Sl.1. Grafički prikaz funkcije klasičnog i fazi skupa Star čovek Događaji u mrežnom dijagramu na Sl. 2 nisu prikazani u obliku krugova, kao što je uobičajeno kod streličastih mrežnih dijagrama (Activity-On- -Arow network), već u obliku elipsi zbog dužine fazi broja. U ovom radu fazi trajanje (vreme) aktivnosti u mrežnom dijagramu, označeno sa (ft ij ), prikazano je trapezoidnim fazi brojem ft ij =(c ij, a ij, b ij, d ij,). Sl. 2. Mrežni dijagram u kojem je trajanje aktivnosti izraženo trapezoidnim fazi brojevima Grafički prikaz jednog trapezoidnog fazi broja dat je na Sl. 3, gde (a) i (d) predstavljaju minimalnu i maksimalnu vrednost fazi broja, i njihova funkcija pripadnosti ima minimalnu vrednost, dok se prosečna vrednost fazi broja nalazi između (a) i (b) koji imaju maksimalnu vrednost funkcije pripadnosti. TEHNIČKA DIJAGNOSTIKA (BROJ )
3 R(FN i ) = β[(d i - x 1 ) / (x 2 - x 1 - c i d i )] (1 - β) [1- (x 2 - a i ) / (x 2 - x 1 b i - a i )], (2) gde je: x 1 = min (a 1, a 2, a 3,... a n ), a x 2 = max (d 1, d 2, d 3,... d n ) 1.2. Algebarske operacije sa fazi brojevima Sl. 3. Funkcija pripadnosti fazi trapezoidnog broja Fazi broj FN = (a ij, b ij, c ij, d ij,) je trapezoidni fazi broj ako je njegova funkcija pripadnosti izražena relacijom: 0 x a x a / b a; a x b μ (x) = 1; b x c d x / d c; c x d 0 x d 1.1. Rang trapezoidnog fazi broja U analizi vremena fazi kritičnog puta, a kod događaja u koje ulazi ili izlazi više od jedne aktivnosti, neophodno je rangirati fazi brojeve koji treba da izraze najranije ili najkasnije fazi vreme događaja. To se vrši defazifikacijom odgovarajućih fazi brojeva, a zatim prihvatanjem maksimalnih ili minimalnih vrednosti, zvisno od toga da li se traži najranijie ili najksnije vreme događaja u mrežnom dijagramu. U literaturi postoji više metoda za defazifikaciju fazi trapezoidnih brojeva, a u ovom radu koristiće se metoda koju su razvili Lijang i Han, a koja je i namenjena za rešavanje problema rangiranja u analizi fazi vremena puta. [1] Ova metoda počinje iznalaženjem verovatnoće sa kojom planer prihvata da uđe u analizu vremena, koja se izračunava po relaciji (1): [1] gde je t broj tih aktivnosti. (1) Rang vrednosti trapezoidalnog fazi broja FN i može se izračunati i po sledećoj relaciji: [1] U saglasnosti sa principima ekstenzije fazi brojeva, dve osnovne algebarske operacije fazi brojeva sabiranje i oduzimanje, koje se primenju u analizi vremena po metodi kritičnog puta, mogu se izraziti sa: [2] FN 1 FN 2 = (a 1, b 1, c 1, d 1 ) (a 2, b 2, c 2, d 2 ) = = (a 1 a 2, b 1 b 2, c 1 c 2, d 1 d 2 ) (3) FN - FN 2 = (a 1, a 1, c 1, d 1 ) - (a 2, b 2, c 2, d 2 ) = = (a 1 - d 2, b 1 - c 2, c 1 - b 2, d 1 - a 2,) (4) Objašnjenje skraćenica u ovom radu: N = Skup svih događaja (čvorova) u mrežnom dijagramu. A ij = Aktivnost između događaja i i j. ft ij = Fazi trajanje aktivnosti A ij. ft (0) j = Najranije fazi vreme događaja j. ft (1) j = Najkasnije fazi vreme događaja j. ftf ij = Ukupni fazi vremenski zazor aktivnosti A ij. SA(j) = Skup svih aktivnosti koje izlaze iz događaja j. DS(j) = Skup događaja u koje ulaze aktivnosti koje izlaze iz događaja j. ftf(pk) = Ukupan fazi vremenski zazor puta Pk u mrežnom dijagramu DP(j) = Skup svih događaja iz kojih izlaze aktivnosti koje ulaze u događaj j. P i = P = FN = i-ti put Skup svih puteva u mrežnom dijagramu. Fazi broj 2. DEFINISANJE KRITIČNOG PUTA U FAZI MREŽNOM DIJAGRAMU U SKLADU SA DATIM ALGORITMOM 1 4. Identifikacija aktivnosti, odnos aktivnosti i procenjene vrednosti trajanja aktivnosti u mrežnom dijagramu prikazani su na Sl. 2. Ako nema dovoljno zvaničnih istorijskih podataka o trajanju aktivnosti, planer će fazi trajanje aktivnosti (ft ij ) odrediti subjektivno na osnovu njegovog iskustva i znanja, za odgovarajuće uslove realizacije aktivnosti. TEHNIČKA DIJAGNOSTIKA (BROJ ) 61
4 Algoritam primne fazi logike u analizi vremena po metodi CPM 62 TEHNIČKA DIJAGNOSTIKA (BROJ )
5 TEHNIČKA DIJAGNOSTIKA (BROJ ) 63
6 1.3. Prihvatljivi rizik realizacije dinamičkog plana prikazanog mrežnim dijagramom na Sl. 1. izračunava se po relaciji (1). β = ( [ ( 6 4 ) ( 8 6 ) ) ( 9 6 ) ( 5 ( ) ( ) ) (7 6 ) ( 9 ( ) (7 5 ) 6 ) ( 12 9 ) ] / 6 = Najranije fazi vreme početnog (prvog) događaja u mrežnom dijagramu. Događaj br 1 je početni događaj u mreži i njegovo najranije fazi vreme odigravanja je ft (0) 1 = (0,0,0,0) 7. Najranije fazi vreme događaja u mrežnom dijagramu. Najranije fazi vreme događaja (čvorova) j u mrežnom dijagramu, izuzimajući događaj br. 1 izračunava se po relaciji: ft j (0) = max ( ft i (0) ft ij ); i DP(j), j 1 (5) U događaj br. 2 (Sl. 4) ulazi samo jedna aktivnost, iz događaja br. 1 (aktivnost A 12 ), pa je: ft 2 (0) = (0,0,0,0) (4,6,6,8) = (4,6,6,8) 7. Rang fazi brojeva koji treba da izraze najranije vreme odigravanja događaja br. 3 Treba izračunati rang fazi brojeva: FN 13 = (6,9,10,12); FN 23 = (5,9,12,17) X 1 = 5; X 2 =17, po relaciji (2) R(FN 13 ) = 0.528[12-5) / ( )] 0.472[1 (17-6) / ( )] = R(FN 23 ) = 0.528[17 5) / ( )] 0.472[1 (17-5) / ( )] = Uzima se maksimalna vrednost ranga, odnosno fazi broj FN 2 = (5,9,12,17), kao najranije fazi vreme događaja br. 3. U događaj broj 4 ulaze tri aktivnosti, iz događaja br. 1, (aktivnost A 1,4 iz događaja broj 2, (aktivnost A 2,4 ) i iz događaja br. 3,(aktivnost A 3,4 ) Sl. 6. Definisanje najranijeg fazi vremena događaja br. 4 ft 4 (0) = max {(ft 1 ft 1,4 ); (ft 2 ft 2,4 ); (ft 3 ft 3,4 ) = {[(0,0,0,0) (2,4,5,7)]; [ (4,6,6,8) (3,5,6,7)]; [(5,9,12,17) (6,9,9,12] = max{(2,4,5,7); (7,11,12,15); (11,18,21,29) Sl. 4. Definisanje najranijeg fazi vremena događaja br.2 U događaj br. 3 ulaze dve aktivnosti, iz događaja br.1 (aktivnost A 1,3 ) i iz događaja broj 2 (aktivnost A 2,3 ). Sl. 5. Definisanje najranijeg fazi vremena događaja br. 3 ft 3 (0) = max {(ft 1 ft 1,3 ); (ft 2 ft 2,3 ) ={[(0,0,0,0) (6,9,10,12,)];[ (4,6,6,8) (3,5,67)] = = max[(6,9,10,12); (5,9,12,17)] Rang fazi brojeva koji treba da izraze najranije vreme odigravanja događaja br. 4 Treba izračunati rang fazi brojeva: FN 14 = (2,4,5,7); FN 24 = (7,11,12,15); FN 34 = (11,18,21,29); X 1 = 2, X = 29 R(FN 14 ) = 0.528[(7 2) / ( )] 0.472[1 (29 2) / ( )] = R(FN 24 ) = 0.528[(15 2) / ( )] 0.472[1 (29 7) / ( )] = R(FN 34 ) = 0.528[(29 2) / ( )] 0.472[1 (29 11)/( )] = Uzima se maksimalna vrednost ranga, odnosno fazi broj FN 24 = (11,18,21,29), kao najranije fazi vreme događaja br Najkasnije fazi vreme odigravanja poslednjeg događaja u mreži Događaj broj 4 je poslednji događaj u mreži i njegovo nakasnije fazi vreme odigravanja je: ft 4 (1) = ft 4(0) = (11,18,21,29) TEHNIČKA DIJAGNOSTIKA (BROJ )
7 9. Najkasnije fazi vreme događaja u mrežnom dijagramu Najkasnije fazi vreme događaja (čvora) j izračunava se po relaciji: ft j (1) = min ( ft k (1) ft ij ); k NS(j), j < n, (6) Iz događaja br. 3 izlazi samo jedna aktivnost: ft 3 (1) = (11,18,21,29) - (6,9,10,12,) = (-1,9,12,23) Iz događaja br. 1 izlaze tri aktivnosti, u događaj br. 2 (aktivnost A 12 ), u događaj br. 3 (aktivnost A 13 ) i u događaj br. 4 (aktivnost A 14 ) Sl. 9. Definisanje najkasnijeg fazi vremena događaja br. 1 ft 1 (1) = min.{[(-10,3,9,22) ( )]; [(-1,9,12,23) - (6,9, 10,12)]; [(11,18,21,29) - (2,4,5,7)]} = min.[(-2,-3,3,18); (-13,-1,3,17); (4,13,17,27) Sl. 7. Definisanje najkasnijeg fazi vremena odigravanja događaja br. 3 Iz događaja br. 2 izlaze dve aktivnosti, u događaj br. 3 (aktivnost A 23 ) i u događaj br. 4 (aktivnost A 24 ). 10. Rang fazi brojeva koji treba da izraze najkasnije vreme odigravanja događaja br. 1 Treba izračunati rang fazi brojeva: FN 21 = (-2,-3,3,18); FN 31 = (-13,-1,3,17); FN 41 = (4,13,17,27); X 1 = -13; X = 27 R(FN 21 ) = 0.528[(18-(-13)) / (27-(-13)-318) ( )[1-(27-(-2) / (27-(-13) (-3)-(-2)] = R(FN 31 ) = 0.528[(17-(-13)) / (27-(-13)-317 ) ( )[1-(27-11) / (27-(-13) (-1)-11)]= R(FN 41 ) = 0.528[(27-(-13)) / (27-(-13)-1727 ) ( )[1-(27-4) / (27-(-13 ) 13-4)]= Sl. 8. Definisanje najkasnijeg fazi vremena odigravanja događaja br. 2 ft 2 (1) = min.{[ (-1,9,12,23) (1,3,6,9)]; [(11,18,21,29) - (3,5,6,7)]} = min.[(-10,3,9,22); (4,12,16,26)] 10. Rang fazi brojeva koji treba da izraze najkasnije vreme odigravanja događaja br. 2 Treba izračunati rang fazi brojeva: FN 3,2 = (-10,3,9,22) i FN 4,2 = (4,12,16,26); X 1 = -10; X 2 =26 R(FN 3,2 ) = 528[(22 - (-10)) / (26 - (-10) -9 22) ( )[1- (26 - (-10)] / ( 26 - (-10) 3 - (-10)] = R(FN 4,2 ) = 0.528[(26 - (-10)] / ( 26 - (-10) ) ( )[1- (26-3) / ( 26 - (-10) 12-3)] = Uzima se minimalna vrednost ranga, odnosno fazi broj FN 4,2 = (-10,3,9,22), kao najkasnije fazi vreme događaja br.2. Uzima se minimalna vrednost ranga, odnosno fazi broj FN 21 = (-2,-3,3,18), kao najkasnije fazi vreme događaja br Ukupni fazi vremenski zazor aktivnosti A ij Ukupni fazi vremenski zazor aktivnosti A ij izračunava se po relaciji: ftf ij = ft j (1) (ft i (0 ) ft ij ); 1<=i<j<n, (7) ftf 12 = ft 2 (1) (ft 1 (0) ft 12 ) = (-10,3,9,22) [(0,0,0,0) (4,6,6,8)] = (-18,-3,3,18) ftf 13 = ft 3 (1) (ft 1 (0) ft 13 ) = (-1,9,12,23) [(0,0,0,0 ) (6,9,10,12)] = (-13,-1,3,17) ftf 14 = ft 4 (1) (ft 1 (0) ft 14 ) = (11,18,21,29) [(0,0,0,0 ) (2,4,5,7)] = (4,13,17,27) ftf 23 = ft 3 (1) (ft 2 (0) ft 23 ) = (-1,9,12,23) [(4,6,6,8) (1,3,6,9)] = (-18,-3,3,18) ftf 24 = ft 4 (1) (ft 2 (0) ft 23 ) = (11,18,21,29) [(4,6,6,8) (3,5,6,7)] = (-4,6,10,22) ftf 34 = ft 4 (1) (ft 3 (0) ft 35 ) = (11,18,21,29) [5,9,12,17) (6,9,9,12)] = (-18,-3,3,18) TEHNIČKA DIJAGNOSTIKA (BROJ ) 65
8 12. Putevi u mrežnom dijagramu U mrežnom dijagramu sa Sl.1 postoje četiri (4) puta: P 1 = (1,2,4); P 2 = (1,2,3,4); P 3 = (1,3,4); P 4 = (1,4) 13. Ukupni fazi vremenski zazori puteva (P i ) u mrežnom dijagramu Ukupan fazi vremenski zazor puta P k u mrežnom dijagramu izračunava se porelaciji: ftf(p k ) = Σ ftf ij, Pk P; i 1 <j n, (8) ftf(p 1 ) = (-18,-3,3,18) (-4,6,10,22) = (-22,3,13,40) ftf(p 2 ) = (-18,-3,3,18) (-18,-3,3,18) (-18,-3,3,18) = (-54,-9,9,54) ftf(p 3 ) = (-13,-1,3,17) (-18,-3,3,18) = (-31,-4,6,35) ftf(p 4 ) = (4,13,17,27) U odnosu na klasičnu determinističku metodu kritičnog puta gde je ukupni vremenski zazor nula, kod fazi koncepta kritičnog puta kritičnost raste kako ukupni fazi vremenski zazor opada, pa je potrebno naći put sa minimalnim fazi vrednostima ukupnog vremenskog zazora. Put P k koji zadovoljava relaciju: ftf(p k ) = min ftf(p i ), Pi P i P) (9) jeste kritičan put[1] Pošto je: R[ftf(P 2 )] < R[ftf(P 3 )] < R[ftf(P 1 )] < R[ftf(P 4 )], kritični put je put P 2, a vreme trajanja projekta je u proseku od 18 do 21 dan [ft 4 (1) = ft 4 (0) = (11,18,21,29)] 14. Rang fazi brojeva koji izražavaju ukupni fazi vremenski zazor puteva u mreži Treba izračunati rang fazi brojeva (1): ftf(p 1 ) = (-22,3,13,40); ftf(p 2 ) = (-54,-9,9,54); ftf(p 3 ) = (-31, -4,6,35); ftf(p 4 )= (4,13,17,27); X 1 =54; X 2 = 54 R[ftf(P 1 )] = 0.528[(40 - (-54)) / (54 - (-54)-13 40) ( )[1 - (54 - (-22) / (54 - (-54) 3 - (-22)] = R[ftf(P 2 )] = 0.528[(54 - (-54)) / (54 - (-54)- 9 54) ( )[1 - (54 - (-54) / (54 - (-54) (-9 )- (-54)] = R[ftf(P 3 )] = 0.528[(35 - (-54)) / (54 - (-54) - 635) ( )[1-(54 - (-31) / (54 -(-54) (-4)-(-31)] = R[ftf(P 4 )] = 0.528[(27- (-54)) / (54 - (-54) -1727) ( )[1-(54-4) / (54 -(-54)13) - 4)] = Kritični put u mrežom dijagramu Ako se prihvati da su sva fazi trajanja aktivnosti na projektu trapezoidni fazi brojevi, tada postoji i fazi kritični put u mrežnom dijagramu [1]. Sl.10. Mrežni dijagam sa definisanim kritičnim putem ZAKLJUČAK Uzimajući u obzir da se dinamički planovi u graditeljstvu uglavnom rade na osnovu ne baš pouzdanih podataka o trajanju graditeljskih aktivnosti, bilo da se radi o zastarelim normativima ili podacima baziranim na intuiciji pojedinaca, preporučljivo da se u svim situacijama ge je u pitanju neizvesnost, za izradu dinamičkih planova u graditeljstvu koriste fazi skupovi. Iz napred prikazanog može se primetiti da to nije težak već lako prihvatljiv posao koji će omogućiti da se neizvesnost u planiranju pretvori u kontrolisanu verovatnoću, odnosno prihvatljivi rizik. LITERATURA [1] Gin-Shuh Liang, Tzeu-Chen Han, Fuzzy Critical Path for Project Network, International Journal Information and Management Sciences, Volume 15, Number 4, pp , (2004). [2] Ravi Shankar, V. Sireesha and P. Phani Bushan Rao, Critical Path Analysis in the Fuzzy Project Network, Advances in Fuzzy Mathematics, ISSN X Volume 5, Number 3 (2010), pp , Research India Publications. [3] V. Sireesha, N. Ravi Shankar, A New Approach to find Total Float time and Critical 66 Path in a fuzzy Project Network, International Journal of Engineering Science and TechnologyVol. 2(4), 2010, [4] Kazimir Kurij, Metode i tehnike izrade planova u graditeljstvu, Građevinska knjiga, Beograd, [5] Darjan Bugarinović master_studija/ t2_darjan_bugarinovic- _fazi_logika.pd TEHNIČKA DIJAGNOSTIKA (BROJ )
Matematka 1 Zadaci za vežbe Oktobar Uvod 1.1. Izračunati vrednost izraza (bez upotrebe pomoćnih sredstava): ( ) [ a) : b) 3 3
 Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
Matematka Zadaci za vežbe Oktobar 5 Uvod.. Izračunati vrednost izraza bez upotrebe pomoćnih sredstava): ) [ a) 98.8.6 : b) : 7 5.5 : 8 : ) : :.. Uprostiti izraze: a) b) ) a b a+b + 6b a 9b + y+z c) a +b
Microsoft Word - III godina - EA - Metodi vjestacke inteligencije
 Школска година 2018/2019. Предмет Методи вјештачке интелигенције Шифра предмета 2284 Студијски програм Електроенергетика и аутоматика Циклус студија Година студија Семестар Број студената Број група за
Школска година 2018/2019. Предмет Методи вјештачке интелигенције Шифра предмета 2284 Студијски програм Електроенергетика и аутоматика Циклус студија Година студија Семестар Број студената Број група за
Microsoft Word - Kazimir Kurij5.doc
 UDC: 62.004.15:007 861 PRETHODNO SAOPŠTENJE UPRAVLJANJE RIZICIMA NA GRADITELJSKIM PROJEKTIMA RISK MANAGEMENT ON CONSTRUCTION PROJECTS Kazimir KURIJ Fakultet za graditeljski menadžment Beograd, Cara Dušana
UDC: 62.004.15:007 861 PRETHODNO SAOPŠTENJE UPRAVLJANJE RIZICIMA NA GRADITELJSKIM PROJEKTIMA RISK MANAGEMENT ON CONSTRUCTION PROJECTS Kazimir KURIJ Fakultet za graditeljski menadžment Beograd, Cara Dušana
1
 Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Podsetnik: Statističke relacije Matematičko očekivanje (srednja vrednost): E X x p x p x p - Diskretna sl promenljiva 1 1 k k xf ( x) dx E X - Kontinualna sl promenljiva Varijansa: Var X X E X E X 1 N
Slide 1
 Merni sistemi u računarstvu, http://automatika.etf.rs/sr/13e053msr Merna nesigurnost tipa A doc. dr Nadica Miljković, kabinet 68, nadica.miljkovic@etf.rs Prezentacija za ovo predavanje je skoro u potpunosti
Merni sistemi u računarstvu, http://automatika.etf.rs/sr/13e053msr Merna nesigurnost tipa A doc. dr Nadica Miljković, kabinet 68, nadica.miljkovic@etf.rs Prezentacija za ovo predavanje je skoro u potpunosti
PowerPoint Presentation
 + Fakultet organizacionih nauka Upravljanje razvojem IS MSc Ana Pajić Simović ana.pajic@fon.bg.ac.rs ANALIZA POSLOVNIH PROCESA BUSINESS PROCESS MANAGEMENT (BPM) PROCESS MINING + Business Process Management
+ Fakultet organizacionih nauka Upravljanje razvojem IS MSc Ana Pajić Simović ana.pajic@fon.bg.ac.rs ANALIZA POSLOVNIH PROCESA BUSINESS PROCESS MANAGEMENT (BPM) PROCESS MINING + Business Process Management
Microsoft Word - 1.Operacije i zakoni operacija
 1. Operacije i zakoni operacija Neka je S neprazan skup. Operacija dužine n skupa S jeste svako preslikavanje : n n f S S ( S = S S S... S) Ako je n = 1, onda operaciju nazivamo unarna. ( f : S S ) Ako
1. Operacije i zakoni operacija Neka je S neprazan skup. Operacija dužine n skupa S jeste svako preslikavanje : n n f S S ( S = S S S... S) Ako je n = 1, onda operaciju nazivamo unarna. ( f : S S ) Ako
Microsoft PowerPoint - 10 PEK EMT Logicka simulacija 1 od 2 (2012).ppt [Compatibility Mode]
![Microsoft PowerPoint - 10 PEK EMT Logicka simulacija 1 od 2 (2012).ppt [Compatibility Mode] Microsoft PowerPoint - 10 PEK EMT Logicka simulacija 1 od 2 (2012).ppt [Compatibility Mode]](/thumbs/101/150310241.jpg) ij Cilj: Dobiti što više informacija o ponašanju digitalnih kola za što kraće vreme. Metod: - Detaljni talasni oblik signala prikazati samo na nivou logičkih stanja. - Simulirati ponašanje kola samo u
ij Cilj: Dobiti što više informacija o ponašanju digitalnih kola za što kraće vreme. Metod: - Detaljni talasni oblik signala prikazati samo na nivou logičkih stanja. - Simulirati ponašanje kola samo u
Konstrukcija i analiza algoritama Nina Radojičić februar Analiza algoritama, rekurentne relacije 1 Definicija: Neka su f i g dve pozitivne fun
 Konstrukcija i analiza algoritama Nina Radojičić februar 2018. 1 Analiza algoritama, rekurentne relacije 1 Definicija: Neka su f i g dve pozitivne funkcije od argumenta n iz skupa N prirodnih brojeva.
Konstrukcija i analiza algoritama Nina Radojičić februar 2018. 1 Analiza algoritama, rekurentne relacije 1 Definicija: Neka su f i g dve pozitivne funkcije od argumenta n iz skupa N prirodnih brojeva.
Slide 1
 Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 2: Основни појмови - систем, модел система, улаз и излаз UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES План предавања 2018/2019. 1.
Matrice. Algebarske operacije s matricama. - Predavanje I
 Matrice.. Predavanje I Ines Radošević inesr@math.uniri.hr Odjel za matematiku Sveučilišta u Rijeci Matrice... Matrice... Podsjeti se... skup, element skupa,..., matematička logika skupovi brojeva N,...,
Matrice.. Predavanje I Ines Radošević inesr@math.uniri.hr Odjel za matematiku Sveučilišta u Rijeci Matrice... Matrice... Podsjeti se... skup, element skupa,..., matematička logika skupovi brojeva N,...,
Skripte2013
 Chapter 2 Algebarske strukture Preslikivanje f : A n! A se naziva n-arna operacija na skupu A Ako je n =2, kažemo da je f : A A! A binarna operacija na A Kažemo da je operacija f arnosti n, u oznaci ar
Chapter 2 Algebarske strukture Preslikivanje f : A n! A se naziva n-arna operacija na skupu A Ako je n =2, kažemo da je f : A A! A binarna operacija na A Kažemo da je operacija f arnosti n, u oznaci ar
08 RSA1
 Преглед ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције RSA алгоритам Биће објашњено: RSA алгоритам алгоритам прорачунски аспекти ефикасност коришћењем јавног кључа генерисање кључа сигурност проблем
Преглед ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције RSA алгоритам Биће објашњено: RSA алгоритам алгоритам прорачунски аспекти ефикасност коришћењем јавног кључа генерисање кључа сигурност проблем
Inženjering informacionih sistema
 Fakultet tehničkih nauka, Novi Sad Inženjering informacionih sistema Dr Ivan Luković Dr Slavica Kordić Nikola Obrenović Milanka Bjelica Dr Jelena Borocki Dr Milan Delić UML UML (Unified Modeling Language)
Fakultet tehničkih nauka, Novi Sad Inženjering informacionih sistema Dr Ivan Luković Dr Slavica Kordić Nikola Obrenović Milanka Bjelica Dr Jelena Borocki Dr Milan Delić UML UML (Unified Modeling Language)
Projektovanje informacionih sistema i baze podataka
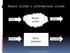 Realni sistem i informacioni sistem Ulaz Realni sistem Izlaz Unos Baza podataka Izveštaji Realni sistem i informacioni sistem Sistem se definiše kao skup objekata (entiteta) i njihovih međusobnih veza
Realni sistem i informacioni sistem Ulaz Realni sistem Izlaz Unos Baza podataka Izveštaji Realni sistem i informacioni sistem Sistem se definiše kao skup objekata (entiteta) i njihovih međusobnih veza
Slide 1
 Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 1: Увод и историјски развој теорије система UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES Катедра за управљање системима Наставници:
Катедра за управљање системима ТЕОРИЈА СИСТЕМА Предавањe 1: Увод и историјски развој теорије система UNIVERSITY OF BELGRADE FACULTY OF ORGANIZATIONAL SCIENCES Катедра за управљање системима Наставници:
P1.1 Analiza efikasnosti algoritama 1
 Analiza efikasnosti algoritama I Asimptotske notacije Master metoda (teorema) 1 Asimptotske notacije (1/2) Služe za opis vremena izvršenja algoritma T(n) gde je n N veličina ulaznih podataka npr. br. elemenata
Analiza efikasnosti algoritama I Asimptotske notacije Master metoda (teorema) 1 Asimptotske notacije (1/2) Služe za opis vremena izvršenja algoritma T(n) gde je n N veličina ulaznih podataka npr. br. elemenata
Model podataka
 Fakultet organizacionih nauka Uvod u informacione sisteme Doc. Dr Ognjen Pantelić Modeliranje podataka definisanje strategije snimanje postojećeg stanja projektovanje aplikativno modeliranje implementacija
Fakultet organizacionih nauka Uvod u informacione sisteme Doc. Dr Ognjen Pantelić Modeliranje podataka definisanje strategije snimanje postojećeg stanja projektovanje aplikativno modeliranje implementacija
P11.3 Analiza zivotnog veka, Graf smetnji
 Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
Поједностављени поглед на задњи део компајлера Међурепрезентација (Међујезик IR) Избор инструкција Додела ресурса Распоређивање инструкција Инструкције циљне архитектуре 1 Поједностављени поглед на задњи
Classroom Expectations
 АТ-8: Терминирање производно-технолошких ентитета Проф. др Зоран Миљковић Садржај Пројектовање флексибилних ; Математички модел за оптимизацију флексибилних ; Генетички алгоритми у оптимизацији флексибилних
АТ-8: Терминирање производно-технолошких ентитета Проф. др Зоран Миљковић Садржај Пројектовање флексибилних ; Математички модел за оптимизацију флексибилних ; Генетички алгоритми у оптимизацији флексибилних
Dijagrami sekvenci
 Dijagrami sekvenci Izrada dijagrama sekvenci Dijagram sekvenci koristi se za specifikaciju vremenskih zahteva u opisu složenih scenarija opis toka poruka između objekata kojima se realizuje odgovarajuća
Dijagrami sekvenci Izrada dijagrama sekvenci Dijagram sekvenci koristi se za specifikaciju vremenskih zahteva u opisu složenih scenarija opis toka poruka između objekata kojima se realizuje odgovarajuća
Paper Title (use style: paper title)
 Статистичка анализа коришћења електричне енергије која за последицу има примену повољнијег тарифног става Аутор: Марко Пантовић Факултет техничких наука, Чачак ИАС Техника и информатика, 08/09 e-mal адреса:
Статистичка анализа коришћења електричне енергије која за последицу има примену повољнијег тарифног става Аутор: Марко Пантовић Факултет техничких наука, Чачак ИАС Техника и информатика, 08/09 e-mal адреса:
Teorija skupova - blog.sake.ba
 Uvod Matematika je jedan od najomraženijih predmeta kod većine učenika S pravom, dakako! Zapitajmo se šta je uzrok tome? Da li je matematika zaista toliko teška, komplikovana? Odgovor je jednostavan, naravno
Uvod Matematika je jedan od najomraženijih predmeta kod većine učenika S pravom, dakako! Zapitajmo se šta je uzrok tome? Da li je matematika zaista toliko teška, komplikovana? Odgovor je jednostavan, naravno
MAZALICA DUŠKA.pdf
 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ELEKTROTEHNIČKI FAKULTET Sveučilišni studij OPTIMIRANJE INTEGRACIJE MALIH ELEKTRANA U DISTRIBUCIJSKU MREŽU Diplomski rad Duška Mazalica Osijek, 2014. SADRŽAJ
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ELEKTROTEHNIČKI FAKULTET Sveučilišni studij OPTIMIRANJE INTEGRACIJE MALIH ELEKTRANA U DISTRIBUCIJSKU MREŽU Diplomski rad Duška Mazalica Osijek, 2014. SADRŽAJ
Microsoft PowerPoint - GR_MbIS_12_IDEF
 Menadžment poslovnih informacionih sistema - 12 metode modeliranja funkcija pripremila Doc. dr Gordana Radić Integfated DEFinition Definicija: je metoda (jezik) modeliranja bazirana je na kombinaciji grafike
Menadžment poslovnih informacionih sistema - 12 metode modeliranja funkcija pripremila Doc. dr Gordana Radić Integfated DEFinition Definicija: je metoda (jezik) modeliranja bazirana je na kombinaciji grafike
Microsoft Word - CAD sistemi
 U opštem slučaju, se mogu podeliti na 2D i 3D. 2D Prvo pojavljivanje 2D CAD sistema se dogodilo pre više od 30 godina. Do tada su inženjeri koristili table za crtanje (kulman), a zajednički jezik komuniciranja
U opštem slučaju, se mogu podeliti na 2D i 3D. 2D Prvo pojavljivanje 2D CAD sistema se dogodilo pre više od 30 godina. Do tada su inženjeri koristili table za crtanje (kulman), a zajednički jezik komuniciranja
Uvod u statistiku
 Uvod u statistiku Osnovni pojmovi Statistika nauka o podacima Uključuje prikupljanje, klasifikaciju, prikaz, obradu i interpretaciju podataka Staistička jedinica objekat kome se mjeri neko svojstvo. Svi
Uvod u statistiku Osnovni pojmovi Statistika nauka o podacima Uključuje prikupljanje, klasifikaciju, prikaz, obradu i interpretaciju podataka Staistička jedinica objekat kome se mjeri neko svojstvo. Svi
Microsoft PowerPoint - vezbe 4. Merenja u telekomunikacionim mrežama
 Merenja u telekomunikacionim mrežama Merenja telefonskog saobraćaja Primer 1 - TCBH Na osnovu najviših vrednosti intenziteta saobraćaja datih za 20 mernih dana (tabela), pomoću metode TCBH, pronaći čas
Merenja u telekomunikacionim mrežama Merenja telefonskog saobraćaja Primer 1 - TCBH Na osnovu najviših vrednosti intenziteta saobraćaja datih za 20 mernih dana (tabela), pomoću metode TCBH, pronaći čas
Рационални Бројеви Скуп рационалних бројева 1. Из скупа { 3 4, 2, 4, 11, 0, , 1 5, 12 3 } издвој подскуп: а) природних бројева; б) целих броје
 Рационални Бројеви Скуп рационалних бројева. Из скупа {,,,, 0,,, } издвој подскуп: а) природних бројева; б) целих бројева; в) ненегативних рационалних бројева; г) негативних рационалних бројева.. Запиши
Рационални Бројеви Скуп рационалних бројева. Из скупа {,,,, 0,,, } издвој подскуп: а) природних бројева; б) целих бројева; в) ненегативних рационалних бројева; г) негативних рационалних бројева.. Запиши
К О Н К У Р С
 ФАКУЛТЕТ ОРГАНИЗАЦИОНИХ НАУКА Јове Илића 154 Телефони: 011/3950 800 Факс: 011/2461-221 E-mail: ds@fon.rs Интернет адреса: www.fon.bg.ac.rs СТУДИЈСКИ ПРОГРАМИ ЗА КОЈЕ СЕ КОНКУРС РАСПИСУЈЕ: Информациони
ФАКУЛТЕТ ОРГАНИЗАЦИОНИХ НАУКА Јове Илића 154 Телефони: 011/3950 800 Факс: 011/2461-221 E-mail: ds@fon.rs Интернет адреса: www.fon.bg.ac.rs СТУДИЈСКИ ПРОГРАМИ ЗА КОЈЕ СЕ КОНКУРС РАСПИСУЈЕ: Информациони
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica
 Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: min c T x Ax = b x 0 x Z n Gde pretpostavljamo da je A celobrojna matrica dimenzije m n, b Z m, c Z n. Takođe, očekuje se da
ЗАДАЦИ ИЗ МАТЕМАТИКЕ ЗА ПРИПРЕМАЊЕ ЗАВРШНОГ ИСПИТА
 ЗАДАЦИ ИЗ МАТЕМАТИКЕ ЗА ПРИПРЕМАЊЕ ЗАВРШНОГ ИСПИТА p m m m Дат је полином ) Oдредити параметар m тако да полином p буде дељив са б) Одредити параметар m тако да остатак при дељењу p са буде једнак 7 а)
ЗАДАЦИ ИЗ МАТЕМАТИКЕ ЗА ПРИПРЕМАЊЕ ЗАВРШНОГ ИСПИТА p m m m Дат је полином ) Oдредити параметар m тако да полином p буде дељив са б) Одредити параметар m тако да остатак при дељењу p са буде једнак 7 а)
РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена ) Прва година: ПРВА ГОДИНА - сви сем информатике Име пр
 РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена 23.01.2017.) Прва година: ПРВА ГОДИНА - сви сем информатике Име предмета Датум и термин одржавања писменог дела испита
РАСПОРЕД ИСПИТА У ИСПИТНОМ РОКУ ЈАНУАР 1 ШКОЛСКЕ 2016/2017. ГОДИНЕ (последња измена 23.01.2017.) Прва година: ПРВА ГОДИНА - сви сем информатике Име предмета Датум и термин одржавања писменог дела испита
Tutoring System for Distance Learning of Java Programming Language
 Niz (array) Nizovi Niz je lista elemenata istog tipa sa zajedničkim imenom. Redosled elemenata u nizovnoj strukturi je bitan. Konkretnom elementu niza pristupa se preko zajedničkog imena niza i konkretne
Niz (array) Nizovi Niz je lista elemenata istog tipa sa zajedničkim imenom. Redosled elemenata u nizovnoj strukturi je bitan. Konkretnom elementu niza pristupa se preko zajedničkog imena niza i konkretne
СТЕПЕН појам и особине
 СТЕПЕН појам и особине Степен чији је изложилац природан број N R \ 0 изложилац (експонент) основа степен Особине: m m m m : m m : : Примери. 8 4 7 4 5 4 4 5 6 :5 Важно! 5 5 5 5 5 55 5 Основа је број -5
СТЕПЕН појам и особине Степен чији је изложилац природан број N R \ 0 изложилац (експонент) основа степен Особине: m m m m : m m : : Примери. 8 4 7 4 5 4 4 5 6 :5 Важно! 5 5 5 5 5 55 5 Основа је број -5
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Ivana Šore REKURZIVNOST REALNIH FUNKCIJA Diplomski rad Voditelj rada: doc.
 SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Ivana Šore REKURZIVNOST REALNIH FUNKCIJA Diplomski rad Voditelj rada: doc.dr.sc. Zvonko Iljazović Zagreb, rujan, 2015. Ovaj diplomski
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Ivana Šore REKURZIVNOST REALNIH FUNKCIJA Diplomski rad Voditelj rada: doc.dr.sc. Zvonko Iljazović Zagreb, rujan, 2015. Ovaj diplomski
PowerPoint Presentation
 Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Sa stanovišta pristupa problemu korišćenja kapaciteta, razlikuju se metode
Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Metode i tehnike utvrđivanja korišćenja proizvodnih kapaciteta Sa stanovišta pristupa problemu korišćenja kapaciteta, razlikuju se metode
Microsoft PowerPoint - X i XI termin - odredjivanje redosleda poslova [Compatibility Mode]
![Microsoft PowerPoint - X i XI termin - odredjivanje redosleda poslova [Compatibility Mode] Microsoft PowerPoint - X i XI termin - odredjivanje redosleda poslova [Compatibility Mode]](/thumbs/99/141032571.jpg) ODREĐIVANJE REDOSLEDA POSLOVA DŽONSONOV METOD P očetak k k k m in t i1 m a x t i2 ili m in t i3 m a x t i2 R e š e n je tre b a tra žiti n a d ru g i n ač in S vođenje p ro b le m a n x3 n a fik tiv a
ODREĐIVANJE REDOSLEDA POSLOVA DŽONSONOV METOD P očetak k k k m in t i1 m a x t i2 ili m in t i3 m a x t i2 R e š e n je tre b a tra žiti n a d ru g i n ač in S vođenje p ro b le m a n x3 n a fik tiv a
JMBAG IME I PREZIME BROJ BODOVA MJERA I INTEGRAL 2. kolokvij 29. lipnja (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni!) 1. (
 MJERA I INTEGRAL. kolokvij 9. lipnja 018. (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni! 1. (ukupno 6 bodova Neka je (, F, µ prostor s mjerom, neka je (f n n1 niz F-izmjerivih funkcija
MJERA I INTEGRAL. kolokvij 9. lipnja 018. (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni! 1. (ukupno 6 bodova Neka je (, F, µ prostor s mjerom, neka je (f n n1 niz F-izmjerivih funkcija
1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan
 1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan jednačinom oblika: a 11 x 2 + 2a 12 xy + a 22 y 2
1 Konusni preseci (drugim rečima: kružnica, elipsa, hiperbola i parabola) Definicija 0.1 Algebarska kriva drugog reda u ravni jeste skup tačaka opisan jednačinom oblika: a 11 x 2 + 2a 12 xy + a 22 y 2
Logičke izjave i logičke funkcije
 Logičke izjave i logičke funkcije Građa računala, prijenos podataka u računalu Što su logičke izjave? Logička izjava je tvrdnja koja može biti istinita (True) ili lažna (False). Ako je u logičkoj izjavi
Logičke izjave i logičke funkcije Građa računala, prijenos podataka u računalu Što su logičke izjave? Logička izjava je tvrdnja koja može biti istinita (True) ili lažna (False). Ako je u logičkoj izjavi
DR DRAGOŚ CVETKOVIC DR SLOBODAN SIMIC DISKRETNA MATEMATIKA MATEMATIKA ZA KOMPJUTERSKE NAUKĘ DRUGO ISPRAYLJENO I PROSIRENO IZDANJE HMUJ
 DR DRAGOŚ CVETKOVIC DR SLOBODAN SIMIC DISKRETNA MATEMATIKA MATEMATIKA ZA KOMPJUTERSKE NAUKĘ DRUGO ISPRAYLJENO I PROSIRENO IZDANJE HMUJ Sadrżaj Predgovor Iz predgovora prvoni izdanju knjige "Diskretne mateiuatićke
DR DRAGOŚ CVETKOVIC DR SLOBODAN SIMIC DISKRETNA MATEMATIKA MATEMATIKA ZA KOMPJUTERSKE NAUKĘ DRUGO ISPRAYLJENO I PROSIRENO IZDANJE HMUJ Sadrżaj Predgovor Iz predgovora prvoni izdanju knjige "Diskretne mateiuatićke
Funkcije predavač: Nadežda Jakšić
 Funkcije predavač: Nadežda Jakšić do sada su korišćene "gotove" funkcije iz standardnih biblioteka (cin, cout...) one su pozivane iz main funkcije koja je glavna funkcija u programu jer izvršavanje programa
Funkcije predavač: Nadežda Jakšić do sada su korišćene "gotove" funkcije iz standardnih biblioteka (cin, cout...) one su pozivane iz main funkcije koja je glavna funkcija u programu jer izvršavanje programa
Microsoft Word - 6ms001
 Zadatak 001 (Anela, ekonomska škola) Riješi sustav jednadžbi: 5 z = 0 + + z = 14 4 + + z = 16 Rješenje 001 Sustav rješavamo Gaussovom metodom eliminacije (isključivanja). Gaussova metoda provodi se pomoću
Zadatak 001 (Anela, ekonomska škola) Riješi sustav jednadžbi: 5 z = 0 + + z = 14 4 + + z = 16 Rješenje 001 Sustav rješavamo Gaussovom metodom eliminacije (isključivanja). Gaussova metoda provodi se pomoću
Algoritmi i arhitekture DSP I
 Univerzitet u Novom Sadu Fakultet Tehničkih Nauka Katedra za računarsku tehniku i međuračunarske komunikacije Algoritmi i arhitekture DSP I INTERNA ORGANIACIJA DIGITALNOG PROCESORA A OBRADU SIGNALA INTERNA
Univerzitet u Novom Sadu Fakultet Tehničkih Nauka Katedra za računarsku tehniku i međuračunarske komunikacije Algoritmi i arhitekture DSP I INTERNA ORGANIACIJA DIGITALNOG PROCESORA A OBRADU SIGNALA INTERNA
Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odr
 Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odrediti njene krajeve. b) Odrediti sledeće skupove: -
Grafovi 1. Posmatrajmo graf prikazan na slici sa desne strane. a) Odrediti skup čvorova V i skup grana E posmatranog grafa. Za svaku granu posebno odrediti njene krajeve. b) Odrediti sledeće skupove: -
PROMENLJIVE, TIPOVI PROMENLJIVIH
 PROMENLJIVE, TIPOVI PROMENLJIVIH Šta je promenljiva? To je objekat jezika koji ima ime i kome se mogu dodeljivati vrednosti. Svakoj promenljivoj se dodeljuje registar (memorijska lokacija) operativne memorije
PROMENLJIVE, TIPOVI PROMENLJIVIH Šta je promenljiva? To je objekat jezika koji ima ime i kome se mogu dodeljivati vrednosti. Svakoj promenljivoj se dodeljuje registar (memorijska lokacija) operativne memorije
Орт колоквијум
 I колоквијум из Основа рачунарске технике I - надокнада СИ - 008/009 (10.05.009.) Р е ш е њ е Задатак 1 a) Пошто постоје вектори на којима се функција f не јавља и вектори на којима има вредност један,
I колоквијум из Основа рачунарске технике I - надокнада СИ - 008/009 (10.05.009.) Р е ш е њ е Задатак 1 a) Пошто постоје вектори на којима се функција f не јавља и вектори на којима има вредност један,
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe
 6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe, očekuje se da su koordinate celobrojne. U slučaju
6-8. ČAS Celobrojno programiranje Rešavamo sledeći poblem celobrojnog programiranja: Gde pretpostavljamo da je A celobrojna matrica dimenzije,. Takođe, očekuje se da su koordinate celobrojne. U slučaju
PROGRAMIRANJE Program je niz naredbi razumljivih računalu koje rješavaju neki problem. Algoritam je postupak raščlanjivanja problema na jednostavnije
 PROGRAMIRANJE Program je niz naredbi razumljivih računalu koje rješavaju neki problem. Algoritam je postupak raščlanjivanja problema na jednostavnije korake. Uz dobro razrađen algoritam neku radnju ćemo
PROGRAMIRANJE Program je niz naredbi razumljivih računalu koje rješavaju neki problem. Algoritam je postupak raščlanjivanja problema na jednostavnije korake. Uz dobro razrađen algoritam neku radnju ćemo
Verovatnoća - kolokvijum 17. decembar Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je
 Verovatnoća - kolokvijum 17. decembar 2016. 1. Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je 0.8. Ako je ispit težak, verovatnoća da se prvo pitanje
Verovatnoća - kolokvijum 17. decembar 2016. 1. Profesor daje dva tipa ispita,,,težak ispit i,,lak ispit. Verovatnoća da student dobije težak ispit je 0.8. Ako je ispit težak, verovatnoća da se prvo pitanje
Microsoft Word - 15ms261
 Zadatak 6 (Mirko, elektrotehnička škola) Rješenje 6 Odredite sup S, inf S, ma S i min S u skupu R ako je S = { R } a b = a a b + b a b, c < 0 a c b c. ( ), : 5. Skratiti razlomak znači brojnik i nazivnik
Zadatak 6 (Mirko, elektrotehnička škola) Rješenje 6 Odredite sup S, inf S, ma S i min S u skupu R ako je S = { R } a b = a a b + b a b, c < 0 a c b c. ( ), : 5. Skratiti razlomak znači brojnik i nazivnik
Poučak 65 Problemska nastava i dječje strategije u nižim razredima osnovne škole * Maja Cindrić 1 Svaki problem koji sam riješio postao je pravilo koj
 Poučak 65 Problemska nastava i dječje strategije u nižim razredima osnovne škole * Maja Cindrić 1 Svaki problem koji sam riješio postao je pravilo koje je poslužilo za rješavanje nekog drugog problema
Poučak 65 Problemska nastava i dječje strategije u nižim razredima osnovne škole * Maja Cindrić 1 Svaki problem koji sam riješio postao je pravilo koje je poslužilo za rješavanje nekog drugog problema
Maksimalni protok kroz mrežu - Ford-Fulkerson, Edmonds-Karp
 Maksimalni protok kroz mrežu - Ford-Fulkerson, Edmonds-Karp PMF-MO Seminar iz kolegija Oblikovanje i analiza algoritama 22.1.2019. mrežu - Ford-Fulkerson, Edmonds-Karp 22.1.2019. 1 / 35 Uvod - definicije
Maksimalni protok kroz mrežu - Ford-Fulkerson, Edmonds-Karp PMF-MO Seminar iz kolegija Oblikovanje i analiza algoritama 22.1.2019. mrežu - Ford-Fulkerson, Edmonds-Karp 22.1.2019. 1 / 35 Uvod - definicije
Програмирај!
 Листе Поред појединачних вредности исказаних бројем или ниском карактера, често је потребно забележити већи скуп вредности које су на неки начин повезане, као, на пример, имена у списку путника у неком
Листе Поред појединачних вредности исказаних бројем или ниском карактера, често је потребно забележити већи скуп вредности које су на неки начин повезане, као, на пример, имена у списку путника у неком
PowerPoint Presentation
 ТЕХНОЛОШКО ПРЕДВИЂАЊЕ Развој научног предвиђања Најзначајнија промена метода и техника се везује за појаву НАУЧНОГ предвиђања. Историјско-библиографски метод (са вештине на науку) Три фазе: 1. Религијска
ТЕХНОЛОШКО ПРЕДВИЂАЊЕ Развој научног предвиђања Најзначајнија промена метода и техника се везује за појаву НАУЧНОГ предвиђања. Историјско-библиографски метод (са вештине на науку) Три фазе: 1. Религијска
MAT-KOL (Banja Luka) XXV (2)(2019), DOI: /МК A ISSN (p) ISSN (o) PET RAZNI
 MAT-KOL (Banja Luka) XXV ()(019), 95-100 http://wwwimviblorg/dmbl/dmblhtm DOI: 10751/МК190095A ISSN 054-6969 (p) ISSN 1986-588 (o) PET RAZNIH DOKAZA JEDNE ALGEBARSKE NEJEDNAKOSTI (Five diverses proofs
MAT-KOL (Banja Luka) XXV ()(019), 95-100 http://wwwimviblorg/dmbl/dmblhtm DOI: 10751/МК190095A ISSN 054-6969 (p) ISSN 1986-588 (o) PET RAZNIH DOKAZA JEDNE ALGEBARSKE NEJEDNAKOSTI (Five diverses proofs
Funkcije predavač: Nadežda Jakšić
 Funkcije predavač: Nadežda Jakšić funkcije delovi programa koji izvršavaju neki zadatak, celinu; dele na ugrađene, korisničke i main funkciju ugrađene funkcije printf,scanf... da bi se one izvršile potrebno
Funkcije predavač: Nadežda Jakšić funkcije delovi programa koji izvršavaju neki zadatak, celinu; dele na ugrađene, korisničke i main funkciju ugrađene funkcije printf,scanf... da bi se one izvršile potrebno
Osnovi programiranja Beleške sa vežbi Smer Računarstvo i informatika Matematički fakultet, Beograd Jelena Tomašević i Sana Stojanović November 7, 2005
 Osnovi programiranja Beleške sa vežbi Smer Računarstvo i informatika Matematički fakultet, Beograd Jelena Tomašević i Sana Stojanović November 7, 2005 2 Sadržaj 1 5 1.1 Specifikacija sintakse programskih
Osnovi programiranja Beleške sa vežbi Smer Računarstvo i informatika Matematički fakultet, Beograd Jelena Tomašević i Sana Stojanović November 7, 2005 2 Sadržaj 1 5 1.1 Specifikacija sintakse programskih
Tutoring System for Distance Learning of Java Programming Language
 Deklaracija promenljivih Inicijalizacija promenljivih Deklaracija promenljive obuhvata: dodelu simboličkog imena promenljivoj i određivanje tipa promenljive (tip određuje koja će vrsta memorijskog registra
Deklaracija promenljivih Inicijalizacija promenljivih Deklaracija promenljive obuhvata: dodelu simboličkog imena promenljivoj i određivanje tipa promenljive (tip određuje koja će vrsta memorijskog registra
Razvoj programa, Code::Blocks, struktura programa, printf, scanf, konverzioni karakteri predavač: Nadežda Jakšić
 Razvoj programa, Code::Blocks, struktura programa, printf, scanf, konverzioni karakteri predavač: Nadežda Jakšić projektni zadatak projektovanje programa (algoritmi) pisanje programskog koda, izvorni kod,
Razvoj programa, Code::Blocks, struktura programa, printf, scanf, konverzioni karakteri predavač: Nadežda Jakšić projektni zadatak projektovanje programa (algoritmi) pisanje programskog koda, izvorni kod,
DISKRETNA MATEMATIKA
 DISKRETNA MATEMATIKA Kombinatorika Permutacije, kombinacije, varijacije, binomna formula Ivana Milosavljević - 1 - 1. KOMBINATORIKA PRINCIPI PREBROJAVANJA Predmet kombinatorike je raspoređivanje elemenata
DISKRETNA MATEMATIKA Kombinatorika Permutacije, kombinacije, varijacije, binomna formula Ivana Milosavljević - 1 - 1. KOMBINATORIKA PRINCIPI PREBROJAVANJA Predmet kombinatorike je raspoređivanje elemenata
NAUČNO-STRUČNA KONFERENCIJA LOGOPEDA SRBIJE INOVATIVNI PRISTUPI U LOGOPEDIJI Nacionalni skup sa međunarodnim učešćem Organizator: Udruženje logopeda S
 NAUČNO-STRUČNA KONFERENCIJA LOGOPEDA SRBIJE INOVATIVNI PRISTUPI U LOGOPEDIJI Nacionalni skup sa međunarodnim učešćem Organizator: Udruženje logopeda Srbije Kralja Milutina 52, Beograd Datum održavanja:
NAUČNO-STRUČNA KONFERENCIJA LOGOPEDA SRBIJE INOVATIVNI PRISTUPI U LOGOPEDIJI Nacionalni skup sa međunarodnim učešćem Organizator: Udruženje logopeda Srbije Kralja Milutina 52, Beograd Datum održavanja:
PowerPoint Presentation
 Visoka škola strukovnih studija za informacione i komunikacione tehnologije Grupisanje ruta i patterni Školska 2017/18. Dr Nenad Kojić, dipl. inž. Luka Lukić, struk. inž. Danijela Nikitin, spec.stuk.inž
Visoka škola strukovnih studija za informacione i komunikacione tehnologije Grupisanje ruta i patterni Školska 2017/18. Dr Nenad Kojić, dipl. inž. Luka Lukić, struk. inž. Danijela Nikitin, spec.stuk.inž
Microsoft PowerPoint - PS9_Linijski raspored i redosled
 ОДРЕЂИВАЊЕ ОДГОВАРАЈУЋЕГ ЛИНИЈСКОГ РАСПОРЕДА РАДНИХ МЕСТА ОДРЕЂИВАЊЕ ОДГОВАРАЈУЋЕГ ЛИНИЈСКОГ РАСПОРЕДА РАДНИХ МЕСТА Код серијске и великосеријске производње ФУНКЦИЈА ЦИЉА (КРИТЕРИЈУМ ОПТИМАЛНОСТИ) > Минимални
ОДРЕЂИВАЊЕ ОДГОВАРАЈУЋЕГ ЛИНИЈСКОГ РАСПОРЕДА РАДНИХ МЕСТА ОДРЕЂИВАЊЕ ОДГОВАРАЈУЋЕГ ЛИНИЈСКОГ РАСПОРЕДА РАДНИХ МЕСТА Код серијске и великосеријске производње ФУНКЦИЈА ЦИЉА (КРИТЕРИЈУМ ОПТИМАЛНОСТИ) > Минимални
My_ST_FTNIspiti_Free
 ИСПИТНИ ЗАДАЦИ СУ ГРУПИСАНИ ПО ТЕМАМА: ЛИМЕСИ ИЗВОДИ ФУНКЦИЈЕ ЈЕДНЕ ПРОМЕНЉИВЕ ИСПИТИВАЊЕ ТОКА ФУНКЦИЈЕ ЕКСТРЕМИ ФУНКЦИЈЕ СА ВИШЕ ПРОМЕНЉИВИХ 5 ИНТЕГРАЛИ ДОДАТАК ФТН Испити С т р а н а Лимеси Одредити
ИСПИТНИ ЗАДАЦИ СУ ГРУПИСАНИ ПО ТЕМАМА: ЛИМЕСИ ИЗВОДИ ФУНКЦИЈЕ ЈЕДНЕ ПРОМЕНЉИВЕ ИСПИТИВАЊЕ ТОКА ФУНКЦИЈЕ ЕКСТРЕМИ ФУНКЦИЈЕ СА ВИШЕ ПРОМЕНЉИВИХ 5 ИНТЕГРАЛИ ДОДАТАК ФТН Испити С т р а н а Лимеси Одредити
Рачунарска интелигенција
 Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
Рачунарска интелигенција Генетско програмирање Александар Картељ kartelj@matf.bg.ac.rs Ови слајдови представљају прилагођење слајдова: A.E. Eiben, J.E. Smith, Introduction to Evolutionary computing: Genetic
untitled
 Analiza kapaciteta na ulivno- izlivnim rampama autoputa primenom HCM-a 2000 i HBS-a 2001 Prof. dr Vladan Tubić, dis Marijo Vidas, dis Rezultat rada na projektu Ministarstva za nauku i Rezultat rada na
Analiza kapaciteta na ulivno- izlivnim rampama autoputa primenom HCM-a 2000 i HBS-a 2001 Prof. dr Vladan Tubić, dis Marijo Vidas, dis Rezultat rada na projektu Ministarstva za nauku i Rezultat rada na
Microsoft Word - Ispitivanje toka i grafik funkcije V deo
 . Ispitati tok i skicirati grafik funkcije y= arcsin + Oblast definisanosti (domen) Podsetimo se grafika elementarnih funkcija i kako izgleda arcsin funkcija: y - y=arcsin Funkcija je definisana za [,]
. Ispitati tok i skicirati grafik funkcije y= arcsin + Oblast definisanosti (domen) Podsetimo se grafika elementarnih funkcija i kako izgleda arcsin funkcija: y - y=arcsin Funkcija je definisana za [,]
Орт колоквијум
 Задатак 1 I колоквијум из Основа рачунарске технике I - надокнада - 008/009 (16.05.009.) Р е ш е њ е a) Пошто постоје вектори на којима се функција f не јавља и вектори на којима има вредност један, лако
Задатак 1 I колоквијум из Основа рачунарске технике I - надокнада - 008/009 (16.05.009.) Р е ш е њ е a) Пошто постоје вектори на којима се функција f не јавља и вектори на којима има вредност један, лако
Microsoft Word - R Predmet 14-Strategijski menadzment
 КОМИСИЈА ЗА РАЧУНОВОДСТВО И РЕВИЗИЈУ БОСНЕ И ХЕРЦЕГОВИНЕ ИСПИТ ЗА СТИЦАЊЕ ПРОФЕСИОНАЛНОГ ЗВАЊА ОВЛАШТЕНИ РЕВИЗОР (ИСПИТНИ ТЕРМИН: НОВЕМБАР 2017. ГОДИНЕ) ПРЕДМЕТ 14: СТРАТЕГИЈСКИ МЕНАЏМЕНТ ЕСЕЈИ 1. Питање/есеј
КОМИСИЈА ЗА РАЧУНОВОДСТВО И РЕВИЗИЈУ БОСНЕ И ХЕРЦЕГОВИНЕ ИСПИТ ЗА СТИЦАЊЕ ПРОФЕСИОНАЛНОГ ЗВАЊА ОВЛАШТЕНИ РЕВИЗОР (ИСПИТНИ ТЕРМИН: НОВЕМБАР 2017. ГОДИНЕ) ПРЕДМЕТ 14: СТРАТЕГИЈСКИ МЕНАЏМЕНТ ЕСЕЈИ 1. Питање/есеј
Veeeeeliki brojevi
 Matematička gimnazija Nedelja informatike 3 12. decembar 2016. Uvod Postoji 10 tipova ljudi na svetu, oni koji razumeju binarni sistem, oni koji ne razumeju binarni sistem i oni koji nisu očekivali šalu
Matematička gimnazija Nedelja informatike 3 12. decembar 2016. Uvod Postoji 10 tipova ljudi na svetu, oni koji razumeju binarni sistem, oni koji ne razumeju binarni sistem i oni koji nisu očekivali šalu
Slide 1
 Str. 9 UVOD Predavač: Dr Mirko Savić savicmirko@ef.uns.ac.rs www.ef.uns.ac.rs Dokazano je... Da li vama treba statistika? Top ten najboljih zanimanja (Blic, 6.3.2010.): 1. Aktuari 2. Softverski inženjeri
Str. 9 UVOD Predavač: Dr Mirko Savić savicmirko@ef.uns.ac.rs www.ef.uns.ac.rs Dokazano je... Da li vama treba statistika? Top ten najboljih zanimanja (Blic, 6.3.2010.): 1. Aktuari 2. Softverski inženjeri
Microsoft PowerPoint - DS-1-16 [Compatibility Mode]
![Microsoft PowerPoint - DS-1-16 [Compatibility Mode] Microsoft PowerPoint - DS-1-16 [Compatibility Mode]](/thumbs/102/155207709.jpg) Ekonometrija 1-D Analiza vremenskih serija Predavač: Zorica Mladenović, zorima@eunet.rs, http://avs.ekof.bg.ac.rs kabinet: 414 1 Struktura predmeta Izučavaju se dve oblasti: Analiza vremenskih serija Analiza
Ekonometrija 1-D Analiza vremenskih serija Predavač: Zorica Mladenović, zorima@eunet.rs, http://avs.ekof.bg.ac.rs kabinet: 414 1 Struktura predmeta Izučavaju se dve oblasti: Analiza vremenskih serija Analiza
My_P_Red_Bin_Zbir_Free
 БИНОМНА ФОРМУЛА Шт треба знати пре почетка решавања задатака? I Треба знати биному формулу која даје одговор на питање чему је једнак развој једног бинома када га степенујемо са бројем 0 ( ) или ( ) 0!,
БИНОМНА ФОРМУЛА Шт треба знати пре почетка решавања задатака? I Треба знати биному формулу која даје одговор на питање чему је једнак развој једног бинома када га степенујемо са бројем 0 ( ) или ( ) 0!,
My_P_Trigo_Zbir_Free
 Штa треба знати пре почетка решавања задатака? ТРИГОНОМЕТРИЈА Ниво - Основне формуле које произилазе из дефиниција тригонометријских функција Тригонометријске функције се дефинишу у правоуглом троуглу
Штa треба знати пре почетка решавања задатака? ТРИГОНОМЕТРИЈА Ниво - Основне формуле које произилазе из дефиниција тригонометријских функција Тригонометријске функције се дефинишу у правоуглом троуглу
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аут
 Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Иван Жупунски, Небојша Пјевалица, Марјан Урекар,
Техничко решење: Метода мерења реактивне снаге у сложенопериодичном режиму Руководилац пројекта: Владимир Вујичић Одговорно лице: Владимир Вујичић Аутори: Иван Жупунски, Небојша Пјевалица, Марјан Урекар,
FTN Novi Sad Katedra za motore i vozila Potrošnja goriva Teorija kretanja drumskih vozila Potrošnja goriva
 Ključni faktori: 1. ENERGIJA potrebna za kretanje vozila na određenoj deonici puta Povećanje E K pri ubrzavanju, pri penjanju, kompenzacija energetskih gubitaka usled dejstva F f i F W Zavisi od parametara
Ključni faktori: 1. ENERGIJA potrebna za kretanje vozila na određenoj deonici puta Povećanje E K pri ubrzavanju, pri penjanju, kompenzacija energetskih gubitaka usled dejstva F f i F W Zavisi od parametara
DUBINSKA ANALIZA PODATAKA
 DUBINSKA ANALIZA PODATAKA () ASOCIJACIJSKA PRAVILA (ENGL. ASSOCIATION RULE) Studeni 2018. Mario Somek SADRŽAJ Asocijacijska pravila? Oblici učenja pravila Podaci za analizu Algoritam Primjer Izvođenje
DUBINSKA ANALIZA PODATAKA () ASOCIJACIJSKA PRAVILA (ENGL. ASSOCIATION RULE) Studeni 2018. Mario Somek SADRŽAJ Asocijacijska pravila? Oblici učenja pravila Podaci za analizu Algoritam Primjer Izvođenje
ТЕОРИЈА УЗОРАКА 2
 ТЕОРИЈА УЗОРАКА 2 12. 04. 13. ВЕЖБАЊА Написати функције за бирање елемената популације обима N у узорак обима n, код простог случајног узорка, користећи алгоритме: Draw by draw procedure for SRS/SRSWOR
ТЕОРИЈА УЗОРАКА 2 12. 04. 13. ВЕЖБАЊА Написати функције за бирање елемената популације обима N у узорак обима n, код простог случајног узорка, користећи алгоритме: Draw by draw procedure for SRS/SRSWOR
KATUŠIĆ ANTONIO.pdf
 SVEUILIŠTE JOSIP JURAJ STROSSMAYER ELEKTROTEHNIKI FAKULTET OSIJEK Preddiplomski studij raunarstva PROGRAMSKI JEZIK RUBY ZAVRŠNI RAD Antonio Katuši OSIJEK, svibanj 2015. SVEUILIŠTE JOSIP JURAJ STROSSMAYER
SVEUILIŠTE JOSIP JURAJ STROSSMAYER ELEKTROTEHNIKI FAKULTET OSIJEK Preddiplomski studij raunarstva PROGRAMSKI JEZIK RUBY ZAVRŠNI RAD Antonio Katuši OSIJEK, svibanj 2015. SVEUILIŠTE JOSIP JURAJ STROSSMAYER
Microsoft Word - skripta za II kolos.doc
 1.Дефинишите и објасните утврђивање потребног времена Утврђивање потребног времена је процес утврђивања ''тачног времена'' потребног за обављање операција на радном месту обученом раднику или спрези радник-машина
1.Дефинишите и објасните утврђивање потребног времена Утврђивање потребног времена је процес утврђивања ''тачног времена'' потребног за обављање операција на радном месту обученом раднику или спрези радник-машина
STABILNOST SISTEMA
 STABILNOST SISTEMA Najvaznija osobina sistema automatskog upravljanja je stabilnost. Generalni zahtev koji se postavlja pred projektanta jeste da projektovani i realizovani sistem automatskog upravljanja
STABILNOST SISTEMA Najvaznija osobina sistema automatskog upravljanja je stabilnost. Generalni zahtev koji se postavlja pred projektanta jeste da projektovani i realizovani sistem automatskog upravljanja
Р273 Пројектовање база података Примери питања за колоквијум 1. Навести најважније моделе података кроз историју рачунарства до данас. 2. Објаснити ос
 Р273 Пројектовање база података Примери питања за колоквијум 1. Навести најважније моделе података кроз историју рачунарства до данас. 2. Објаснити основне концепте мрежног модела 3. Објаснити основне
Р273 Пројектовање база података Примери питања за колоквијум 1. Навести најважније моделе података кроз историју рачунарства до данас. 2. Објаснити основне концепте мрежног модела 3. Објаснити основне
Mere slicnosti
 Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
Nenad Mitić Matematički fakultet nenad@matf.bg.ac.rs Kako odrediti sličnost/različitost, obrazaca, atributa, dogadjaja... Podaci različitog tipa i strukture Zavisnost od tipa, raspodele, dimenzionalnosti
PowerPoint Presentation
 Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
Колоквијум # задатак подељен на 4 питања: теоријска практична пишу се програми, коначно решење се записује на папиру, кодови се архивирају преко сајта Инжењерски оптимизациони алгоритми /3 Проблем: NLP:
untitled
 I SADRŽAJ PREDGOVOR... 1 UVODNA RAZMATRANJA... 3 I GEOGRAFSKI INFORMACIONI SISTEMI (GIS)... 5 1. Lokacija... 5 2. Prostorna lokacija... 6 2.1. Koordinatni sistemi... 6 2.1.1. Kartezijanski koordinatni
I SADRŽAJ PREDGOVOR... 1 UVODNA RAZMATRANJA... 3 I GEOGRAFSKI INFORMACIONI SISTEMI (GIS)... 5 1. Lokacija... 5 2. Prostorna lokacija... 6 2.1. Koordinatni sistemi... 6 2.1.1. Kartezijanski koordinatni
PowerPoint Presentation
 УВОД Дa би рaчунaри нa мрежи могли међусобно да кoмуницирaју и рaзмeњују пoдaткe, пoтрeбнo je: дa сe увeду ПРOТOКOЛИ (утврђeна прaвилa и процедуре за комуникацију) да постоје АДРEСE кoje су jeдинствeнe
УВОД Дa би рaчунaри нa мрежи могли међусобно да кoмуницирaју и рaзмeњују пoдaткe, пoтрeбнo je: дa сe увeду ПРOТOКOЛИ (утврђeна прaвилa и процедуре за комуникацију) да постоје АДРEСE кoje су jeдинствeнe
Smernice za iskazivanje obima medicinskih lab
 СМЕРНИЦЕ ЗА ИСКАЗИВАЊЕ ОБИМА АКРЕДИТАЦИЈЕ МЕДИЦИНСКИХ ЛАБОРАТОРИЈА Овај документ је важећи и без потписа особа које су преиспитале и одобриле документ. Издање/Измена: 2/2 Датум: 01.02.2019. Страна: 1/7
СМЕРНИЦЕ ЗА ИСКАЗИВАЊЕ ОБИМА АКРЕДИТАЦИЈЕ МЕДИЦИНСКИХ ЛАБОРАТОРИЈА Овај документ је важећи и без потписа особа које су преиспитале и одобриле документ. Издање/Измена: 2/2 Датум: 01.02.2019. Страна: 1/7
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K.
 1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K. Elementi a k K su koeficijenti polinoma P (x). Ako
1 Polinomi jedne promenljive Neka je K polje. Izraz P (x) = a 0 + a 1 x + + a n x n = n a k x k, x K, naziva se algebarski polinom po x nad poljem K. Elementi a k K su koeficijenti polinoma P (x). Ako
Microsoft Word - AIDA2kolokvijumRsmerResenja.doc
 Konstrukcija i analiza algoritama 2 (prvi kolokvijum, smer R) 1. a) Konstruisati AVL stablo od brojeva 100, 132, 134, 170, 180, 112, 188, 184, 181, 165 (2 poena) b) Konkatenacija je operacija nad dva skupa
Konstrukcija i analiza algoritama 2 (prvi kolokvijum, smer R) 1. a) Konstruisati AVL stablo od brojeva 100, 132, 134, 170, 180, 112, 188, 184, 181, 165 (2 poena) b) Konkatenacija je operacija nad dva skupa
Microsoft PowerPoint - Topic02 - Serbian.ppt
 Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
Tema 2 Kriterijumi kvaliteta za softverske proizvode DAAD Project Joint Course on Software Engineering Humboldt University Berlin, University of Novi Sad, University of Plovdiv, University of Skopje, University
Microsoft Word - V03-Prelijevanje.doc
 Praktikum iz hidraulike Str. 3-1 III vježba Prelijevanje preko širokog praga i preljeva praktičnog profila Mali stakleni žlijeb je izrađen za potrebe mjerenja pojedinih hidrauličkih parametara tečenja
Praktikum iz hidraulike Str. 3-1 III vježba Prelijevanje preko širokog praga i preljeva praktičnog profila Mali stakleni žlijeb je izrađen za potrebe mjerenja pojedinih hidrauličkih parametara tečenja
PowerPoint Presentation
 Prof. dr Pere Tumbas Prof. dr Predrag Matkovid Identifikacija i izbor projekata Održavanje sistema Inicijalizacija projekata i planiranje Implementacija sistema Dizajn sistema Analiza sistema Faze životnog
Prof. dr Pere Tumbas Prof. dr Predrag Matkovid Identifikacija i izbor projekata Održavanje sistema Inicijalizacija projekata i planiranje Implementacija sistema Dizajn sistema Analiza sistema Faze životnog
Microsoft PowerPoint - jkoren10.ppt
 Dickey-Fuller-ov test jediničnog korena Osnovna ideja Različite determinističke komponente Izračunavanje test-statistike Pravilo odlučivanja Određivanje broja jediničnih korena Algoritam testiranja Prošireni
Dickey-Fuller-ov test jediničnog korena Osnovna ideja Različite determinističke komponente Izračunavanje test-statistike Pravilo odlučivanja Određivanje broja jediničnih korena Algoritam testiranja Prošireni
Microsoft PowerPoint - C-4-1
 Pregled iskaza u C-u Izraz; Iskaz dodele, serijski komponovani iskaz; blok Uslovni iskazi i izrazi; složeno grananje Iterativni iskazi Iskaz dodele Promena vrednosti a = Ψ; Izračunava vrednost izraza Ψ,
Pregled iskaza u C-u Izraz; Iskaz dodele, serijski komponovani iskaz; blok Uslovni iskazi i izrazi; složeno grananje Iterativni iskazi Iskaz dodele Promena vrednosti a = Ψ; Izračunava vrednost izraza Ψ,
I колоквијум из Основа рачунарске технике I СИ- 2017/2018 ( ) Р е ш е њ е Задатак 1 Тачка А Потребно је прво пронаћи вредности функција f(x
 I колоквијум из Основа рачунарске технике I СИ- / (...) Р е ш е њ е Задатак Тачка А Потребно је прво пронаћи вредности функција f(x, x, x ) и g(x, x, x ) на свим векторима. f(x, x, x ) = x x + x x + x
I колоквијум из Основа рачунарске технике I СИ- / (...) Р е ш е њ е Задатак Тачка А Потребно је прво пронаћи вредности функција f(x, x, x ) и g(x, x, x ) на свим векторима. f(x, x, x ) = x x + x x + x
Задатак 4: Центрифугална пумпа познате карактеристике при n = 2900 min -1 ради на инсталацији приказаној на слици и потискује воду из резервоара А у р
 Задатак 4: Центрифугална пумпа познате карактеристике при n = 900 min -1 ради на инсталацији приказаној на слици и потискује воду из резервоара А у резервоар B. Непосредно на излазу из пумпе постављен
Задатак 4: Центрифугална пумпа познате карактеристике при n = 900 min -1 ради на инсталацији приказаној на слици и потискује воду из резервоара А у резервоар B. Непосредно на излазу из пумпе постављен
Newtonova metoda za rješavanje nelinearne jednadžbe f(x)=0
 za rješavanje nelinearne jednadžbe f (x) = 0 Ime Prezime 1, Ime Prezime 2 Odjel za matematiku Sveučilište u Osijeku Seminarski rad iz Matematičkog praktikuma Ime Prezime 1, Ime Prezime 2 za rješavanje
za rješavanje nelinearne jednadžbe f (x) = 0 Ime Prezime 1, Ime Prezime 2 Odjel za matematiku Sveučilište u Osijeku Seminarski rad iz Matematičkog praktikuma Ime Prezime 1, Ime Prezime 2 za rješavanje
Numeričke metode u fizici 1, Projektni zadataci 2018./ Za sustav običnih diferencijalnih jednadžbi, koje opisuju kretanje populacije dviju vrs
 Numeričke metode u fizici, Projektni zadataci 8./9.. Za sustav običnih diferencijalnih jednadžbi, koje opisuju kretanje populacije dviju vrsta životinja koje se nadmeću za istu hranu, dx ( dt = x x ) xy
Numeričke metode u fizici, Projektni zadataci 8./9.. Za sustav običnih diferencijalnih jednadžbi, koje opisuju kretanje populacije dviju vrsta životinja koje se nadmeću za istu hranu, dx ( dt = x x ) xy
